Графическое решение матричной игры
Если число стратегий одного из игроков равно двум, то для нахождения оптимальных стратегий можно легко воспользоваться графическим методом.
Пусть платежная матрица имеет вид
.
Для произвольной стратегии второго игрока, контролирующего столбцы, имеем выигрыш первого игрока
,
поскольку, как сказано раньше,
, 
.
Графиком зависимости 
будет некоторая прямая. Для разных стратегий, то есть для разных 
, получаются разные прямые.
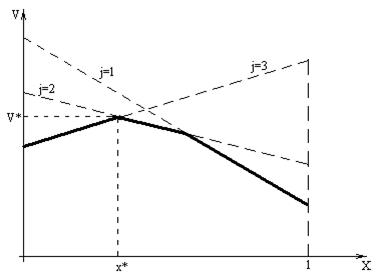
Рассмотрим прямоугольную систему координат, где по оси абсцисс откладывается единичный отрезок A1A2; точка A1 изображает стратегию A1 , а точка A2 изображает стратегию A2. Все промежуточные точки этого отрезка — смешанные стратегии первого игрока, причем расстояние до правого конца отрезка — это вероятность p1 стратегии A1, расстояние до левого конца отрезка это вероятность p2 стратегии A2. На перпендикулярах х=0 и х=1 откладываем выигрыши при стратегиях A1 и A2 соответственно (Рис.3.1).
Рис. 3.1. Графическое нахождение цены игры
На рис. 3.1 изображен случай 
для игры 2 
3. Из принципа минимакса следует, что надо взять нижнюю огибающую всех прямых, соответствующих стратегиям второго игрока (она показана на рисунке жирной линией), а на этой ломаной, обязательно обращенной выпуклостью вверх, надо найти вершину, имеющую максимальное значение v*. Абсцисса этой точки x* и будет искомым значением p1*.
Геометрически можно определять и оптимальную стратегию игрока В для игры 
, но в этом случае строится не нижняя, а верхняя граница выигрыша и на ней определяется не максимум, а минимум.
Алгоритм геометрического решения игры 2×N
1. Откладываем горизонтальный отрезок [0,1], каждая точка которого соответствует смешанной стратегии игрока A. В концах этого отрезка проводим два перпендикуляра. Левый соответствует чистой стратегии A1, правый — чистой стратегии A2 игрока A.
2. На левом перпендикуляре от точки 0 его пересечения с горизонтальным отрезком откладываем (как на вертикальной числовой оси) все элементы первой строки платежной матрицы. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второй строки платежной матрицы. При этом масштабы на обоих перпендикулярах должны быть одинаковые, но не обязаны совпадать с масштабом отрезка [0,1].
3. Каждую пару точек, изображающих элементы a1j, a2j, j=1. n, стоящих в j-м столбце платежной матрицы, соединяем отрезком a1j, a2j . Таким образом будут построены n отрезков, представляющих собой графики n линейных функций
4. Находим нижнюю огибающую семейства построенных отрезков a1j, a2j, представляющую собой выпуклую вверх ломаную. Затем находим максимальную точку нижней огибающей. Абсцисса р o этой точки определяет оптимальную смешанную стратегию P o =(1- p o , p o ) игрока A. Ордината наивысшей точки нижней огибающей равна цене игры V.
5. Верхний из концов нижней огибающей, лежащих на перпендикулярах, есть нижняя цена игры в чистых стратегиях, т.е. a.Нижний из верхних концов отрезковa1j, a2j, j=1. n, есть верхняя цена игры в чистых стратегиях b.
6. Элемент платежной матрицы, изображающая точка которого является нижней на перпендикуляре, где она лежит, и верхним концом отрезка, на котором она лежит, будет седловой точкой игры. В этом случае чистая стратегия игрока B, номер которой совпадает со вторым индексом седловой точки, является оптимальной.
Пример 4. Графически решить игру: 
Действуя по алгоритму геометрического нахождения игры 2×N (рисунок 3.2), находим, что цена игры V=3,5, нижняя цена игры: a=2, верхняя цена игры: b=4, оптимальная стратегия игрока A: P o =(1/2,1/2).
Алгоритм геометрического решения игры М×2
1. Откладываем горизонтальный отрезок [0,1], каждая точка которого
соответствует смешанной стратегии игрока B. В концах этого отрезка проводим два перпендикуляра. Левый соответствует чистой стратегии B1, правый — чистой стратегии B2игрока B.
2. На левом перпендикуляре от точки 0 его пересечения с горизонтальным отрезком откладываем (как на вертикальной числовой оси) все элементы первого столбца платежной матрицы. На правом перпендикуляре от точки 1 его пересечения с отрезком [0,1] откладываем (как на вертикальной числовой оси) все элементы второго столбца платежной матрицы. При этом масштабы на обоих перпендикулярах должны быть одинаковые, но не обязательно совпадающие с масштабом отрезка [0,1].
3. Каждую пару точек, изображающих элементы ai1, ai2, i=1. m, стоящих в i-той строке платежной матрицы, соединяем отрезком ai1, ai2 . Таким образом будут построены m отрезков, представляющих собой графики m линейных функций, зависящих от вероятности q: H(Ai,Q)=(ai2-ai1)q+ai1, i=1. m, q Î[0,1].
4. Находим верхнюю огибающую семейства построенных отрезков ai1, ai2 , представляющую собой выпуклую вниз ломаную. Затем находим минимальную точку верхней огибающей. Абсцисса q o этой точки определяет оптимальную смешанную стратегию Q o =(1-q o ,q o ) игрока B. Ордината наинизшей точки верхней огибающей равна цене игры V.
5. Верхний из нижних концов отрезков ai1, ai2 есть нижняя цена игры в чистых стратегиях, т.е. a. Нижний из концов верхней огибающей (лежащих на перпендикулярах) есть верхняя цена игры в чистых стратегиях, т.е. b.
6. Элемент платежной матрицы, изображающая точка которого является нижним концом отрезка, на котором она лежит, и верхней на перпендикуляре,на котором она лежит, будет седловой точкой игры. В этом случае чистая стратегия игрока A, номер которой совпадает с первым индексом седловой точки, является оптимальной.
Пример 5. Графически решить игру: 
Действуя по алгоритму геометрического нахождения игры М×2
(рисунок 3.3), находим, что цена игры V=4, нижняя цена игры: a=3, верхняя цена игры: b=5, оптимальная стратегия игрока B: Q o =(2/3, 1/3).
Пример 9. Решить графически игру, заданную платежной матрицей: 
Нижняя цена игры равна а11=1,5. Верхняя цена игры равна а21=2, седловая точка отсутствует.
Для игрока А решение представлено на рис. 3.4. Точка N определяет оптимальную стратегию, а ордината — цену игры v. Найдем точку пересечения соответствующих прямых:
Рис. 3.4. Решение матричной игры для игрока А
Следовательно, оптимальная стратегия игрока А заключается в выборе стратегии А1 с вероятностью 0,6 и стратегии А2 с вероятностью 0,4. При этом цена игры v = 1,8.
Для игрока В решение представлено на рис. 3.5. Находя точку пересечения соответствующих прямых, получаем М(0,2; 1,8).
Рис. 3.5. Решение матричной игры для игрока В
Следовательно, оптимальная стратегия игрока В заключается в выборе стратегии В1 с вероятностью 0,8 и стратегии В2 с вероятностью
0,2 = 1 – 0,8. При этом цена игры v = 1,8.
Оптимальное решение игры найдено.
Пример 10. Найти решение игры, заданной матрицей
Проверим наличие седловой точки
Так как 
, седловой точки нет. Решим матричную игру графически. Построим прямые, соответствующие стратегиям игрока А.
Ломанная 
изображает верхнюю границу выигрыша игрока А. На нем определяем К с минимальной ординатой, которая и есть цена игры 
. Оптимальные стратегии для игрока А – вторая и третья.
Матрица оптимальных стратегий имеет вид
, 
,
, 
,
, 
,
, 
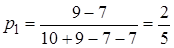
Следовательно, решение игры таково:
, 
, 
Пример 11. Решить матричную игру
Решение. Проверим наличие седловой точки
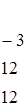
Здесь 
– седловой точки нет.
Решим матричную игру графически. Построим прямые, соответствующие стратегиям игрока В.
Ломаная 
соответствует нижней границе выигрыша. На ней определяем точку К с максимальной ординатой, которая и есть цена игры 
. Оптимальные стратегии для игрока В – первая и четвертая.
Матрица оптимальных стратегий имеет вид
, 
,
, 
,
, 
, 
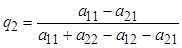
При этом 
ЧТО И КАК ПИСАЛИ О МОДЕ В ЖУРНАЛАХ НАЧАЛА XX ВЕКА Первый номер журнала «Аполлон» за 1909 г. начинался, по сути, с программного заявления редакции журнала.
ЧТО ПРОИСХОДИТ ВО ВЗРОСЛОЙ ЖИЗНИ? Если вы все еще «неправильно» связаны с матерью, вы избегаете отделения и независимого взрослого существования.
Конфликты в семейной жизни. Как это изменить? Редкий брак и взаимоотношения существуют без конфликтов и напряженности. Через это проходят все.
Система охраняемых территорий в США Изучение особо охраняемых природных территорий(ООПТ) США представляет особый интерес по многим причинам.
Не нашли то, что искали? Воспользуйтесь поиском гугл на сайте:
Источник
