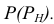Решение задачи способом вспомогательных плоскостей

Способ вспомогательных секущих плоскостей в начертательной геометрии с примером

Способ вспомогательных секущих плоскостей:

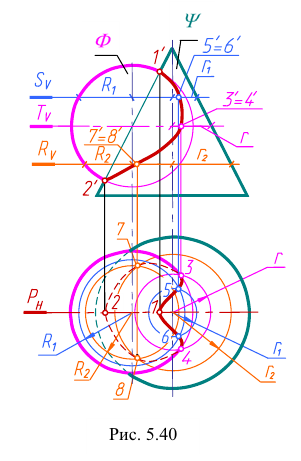
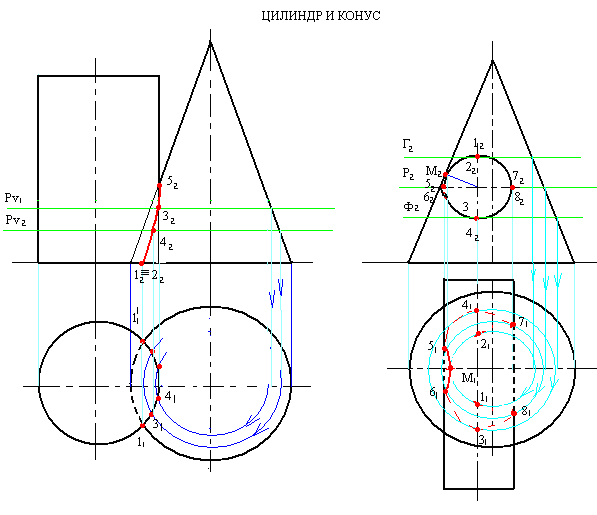
Рассмотрим применение вспомогательных секущих плоскостей на примере построения линии пересечения сферы с конусом вращения (рис.5.40).

Для построения линии пересечения заданных поверхностей в ка­честве вспомогательных плоскостей необходимо использовать фронтальную плоскость Р и ряд горизонтальных плоскостей (S, Т, R).

Построение начинаем с определения проекций характерных точек. Проводим фронтальную плоскость

Вспомогательные горизонтальные плоскости пересекают сферу и конус по окружностям.

Проекции 3′ и 4′ точек, лежащих на экваторе сферы, находим с помощью горизонтальной плоскости 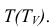Она проходит через центр сферы. Плоскость пересекает сферу по экватору и конус по окружности радиуса В пересечении горизонтальных проекций этих линий и нахо­дим горизонтальные проекции 3 и 4 . Горизонтальные проекции точек 3 и 4 являются точками границы видимости линии пересечения на этой проекции. Промежуточные точки (точки 5, 6, 7, X) находим с помощью вспомогательных горизонтальных плоскостей Полученные точки соединим плавной кривой линией с учетом видимости.

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Способ вспомогательных сфер
• Выполнение и оформление чертежей по ГОСТ и ЕСКД
• Виды в инженерной графике
• Разрезы в инженерной графике
• Построение проекций линий пересечения конуса плоскостью
• Развертка поверхности конуса
• Шаровая поверхность
• Винтовые поверхности

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник

Решение задачи способом вспомогательных плоскостей

Простейшая позиционная задача с использованием этого метода — оценка взаимного расположения прямой и плоскости. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в , последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рис.150).

Рисунок 1 50. Метод вспомогательных секущих плоскостей

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a , параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю, когда прямая а пересекает плоскость a .

Таким образом возможны три случая относительного расположения прямой и плоскости:

Вспомогательные секущие плоскости чаще всего выбирают перпендикулярными или параллельными плоскости проекций.

Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

если образующие (окружности) расположены в общих плоскостях уровня;

если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;

линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

Источник

Метод вспомогательных секущих плоскостей

Для построения линии пересечения двух поверхностей часто применяют метод вспомогательных секущих плоскостей. Смысл этого метод заключается в том, что вводят дополнительную секущую плоскость, которая пересекает обе поверхности. Затем строят линии пересечения обеих поверхностей секущей плоскостью. Точка пересечения этих линий и есть общая точка этих поверхностей. Пересекая поверхности рядом дополнительных плоскостей, получают множество точек, общих для пересекающихся поверхностей.

Как выбрать положение или вид этих вспомогательных плоскостей?

Дополнительные плоскости подбирают таким образом, чтобы они в пересечении с поверхностями давали простые линии пересечения, например, окружности или прямые. Кроме того, эти линии при проецировании на плоскости проекций, должны проецироваться в натуральную величину. Для этих целей подходят обычно плоскости уровня. Рассмотрим на примере работу с одной плоскостью, которую выберем перпендикулярно оси вращения конуса (рис.25).

При решении задач по построению линии пересечения поверхностей необходимо находить характерные точки линии пересечения. Эти точки, как правило, являются точками пересечения очерковых образующих, если поверхности имеют общую ось симметрии, как в примере, рассмотренном на рис.25. Так как эти точки лежат на очерке (точки С и К), то их горизонтальные проекции лежат на оси симметрии поверхностей (рис.26).

Источник

Способ вспомогательных секущих плоскостей

Суть способа – вспомогательная секущая плоскость одновременно пересекает поверхности каждого тела и образует фигуры сечения, контуры которых пересекаются. Точки пересечения контуров соединяют.

Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.

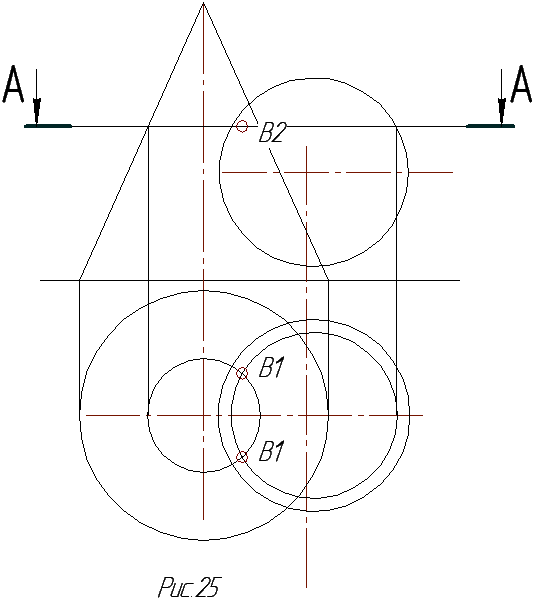
Точки 1 (1₂₎, 5 ( 5₁) и 5 / (5₁ / ) являются очевидными – это точки пересечения очерковых и оснований конусов. Найдём соответствующие вторые проекции этих точек.

Проведём горизонтальную плоскость Р₂, которая рассечет оба конуса. В сечении конусов будут окружностиR₁= А₂В₂/2 иR₂ = С₂D₂/2 , причем их фронтальными проекциями являются прямые. Построим горизонтальные проекции этих сечений – окружности радиусомR₁иR₂.

На пересечении этих окружностей сечений на П₁определим горизонтальную проекцию общей точки – 2₁(2₁ / ). Фронтальную проекцию точек 2 и 2 / определим по линиям связи на секущей плоскости Р₂.

Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.

При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна П₂. Значит, на П₂линия пересечения совпадет с контуром основания цилиндра, т.е. фронтальной проекцией линии пересечения будет являться фронтальная проекция цилиндра.

Построив горизонтальную проекцию линии пересечения, на П₂на пересечении горизонтальной оси симметрии цилиндра с проекцией цилиндра наметим точки 5₂, 6₂, 7₂, 8₂– точки границы видимости линии пересечения, лежащие на экваторе цилиндра.

На П₁точки линии пересечения, лежащие выше экватора будут видимы, а точки, лежащие ниже экватора – невидимы.

Способ вспомогательных сфер

Этот метод можно применять при соблюдении следующих условий :

— пересекающиеся поверхности должны быть поверхностями вращения;

— их оси должны пересекаться ; точка пересечения осей является центром вспомогательных сфер;

— их оси должны быть // какой-либо плоскости проекций.

Сфера R_min должна касаться образующей большего тела, а меньшее тело – пересекать.

Сфера R_min определяется как большее расстояние от центра сфер до образующих обоих тел — перпендикуляры из центра сфер к очерковым образующим. Больший перпендикуляр и будет являться радиусом минимальной сферы.

Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.

1. Определяем очевидные точки 12(11) и 22(21)

2. Восстанавливаем перпендикуляры из центра сфер О₂к очерковым образующим цилиндра и конуса. Перпендикуляр к цилиндру О₂F₂ больше, чем перпендикуляр к образующей конуса. Значит, О₂F₂=Rи будет являться радиусом минимальной сферы. На П₂проводим из центра О₂этим радиусомRокружность, которая рассечет и конус и цилиндр по окружностям, фронтальной проекцией которых будут прямые – сечение конуса А₂В₂и сечение цилиндра С₂F₂.

На пересечении этих сечений определяем фронтальную проекцию точки 3 – 3₂.

3. На П₁строим горизонтальную проекцию сечения конуса, на котором находится точка 3 – окружность радиусом А₂В₂/ 2, на которой по линии связи определяем точки 3₁и 3₁ / .

Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.

Большее тело поглощает меньшее.

Видимость линии пересечения определяем следующим образом:

— на пересечении фронтальной проекции линии пересечения с осью симметрии цилиндра намечаем точку К₂(К₁и К₁ / определяем на П₁на очерковых образующих цилиндра);

— часть линии, находящаяся выше точки К – видимая. Точка К – граница видимости.

Вопросы для самопроверки

В чем заключается метод вспомогательных секущих плоскостей?

В чем заключается метод вспомогательных секущих сфер?

Источник

Решение задачи способом вспомогательных плоскостей

Контрольные задания по теме: эпюр № 4, эпюр № 5 (вариант назначает преподаватель)

При решении задач на взаимное пересечение поверхностей требуется, как правило, найти линию общую для двух или более поверхностей. В случае пересечения гранных поверхностей линией пересечения является ломаная, если пересекаются гранная поверхность и поверхность вращения, то это плоские кривые. Поверхности вращения пересекаются по пространственной кривой.

Существуют следующие случаи взаимного пересечения поверхностей:

1) частичное врезание — когда часть образующих или ребер одной поверхности пересекаются частью образующих или ребер другой. В этом случае линия взаимного пересечения представляет собой замкнутую пространственную кривую или ломаную;

2) полное проницание — когда все образующие или грани одной поверхности пересекаются с другой. В этом случае линия пересечения распадается на две отдельных кривых или ломаных;

3) одностороннее внутреннее соприкасание — пересекающиеся поверхности имеют в одной точке общую плоскость касания. Кривая линия пересечения в этом случае пересекается сама с собой в точке касания;

4) двойное соприкасание — пересекающиеся поверхности имеют две общие касательные плоскости. При этих условиях в пересечении участвуют все образующие одной поверхности и все образующие второй. В этом случае линия пересечения распадается на две плоские кривые, которые пересекаются в точке пересечения касательных плоскостей (теорема Монжа).

Для построения линии пересечения двух поверхностей их пересекают третьей поверхностью, которую называют посредником. В качестве вспомогательных поверхностей выбирают такие, которые пересекали бы данные поверхности по простым линиям — окружностям или прямым. Обычно поверхности — посредники — это плоскости или сферы.

Прежде чем решить вопрос, какую вспомогательную поверхность выбрать, следует выяснить, не занимает ли одна из данных поверхностей проецирующее положение, так как в этом случае решение задачи значительно упрощается. Одна из проекций линии пересечения будет совпадать с очерком проецирующей поверхности. И решение сводится к построению недостающей проекции линии, принадлежащей поверхности по одной ее проекции и по проекциям поверхностей.

Рассмотрим пример пересечения двух поверхностей вращения — конуса и цилиндра. Условие задачи дано на рисунке 53. Цилиндр является фронтально — проецирующей поверхностью, поэтому на фронтальной плоскости проекций линия пересечения будет совпадать с очерком цилиндра. Выбираем опорные точки, лежащие на осях цилиндра и конуса, а также на очерке конуса. Проекции точек находим при помощи вспомогательных секущих плоскостей. Точки 4 и 5 являются границей видимости линии пересечения на горизонтальной плоскости.

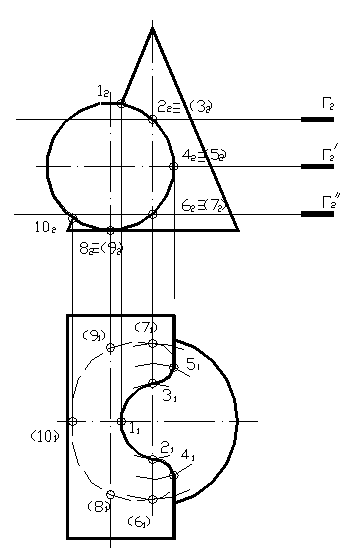
Рисунок 53

1. Какие бывают случаи взаимного пересечения поверхностей?

2. Какая линия получится при пересечении двух гранных поверхностей? Двух поверхностей вращения?

3. Какие точки называются опорными?

4. Как определять видимость линии пересечения и поверхностей?

5. Какие способы построения линии взаимного пересечения поверхностей вы знаете?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник