Решение задачи способом вращения

Решение задачи способом вращения

Контрольные задания по теме: Рабочая тетрадь задача 50

Трудоемкость и точность графического решения задач часто зависит не только от сложности задач, но и от того, какое положение занимают геометрические фигуры по отношению к плоскостям проекций. Наиболее выгодными являются положения, параллельные плоскостям проекций или перпендикулярные им.

Переход от общего положения геометрической фигуры к частному можно осуществить двумя путями:

а) перемещением в пространстве проецируемой фигуры так, чтобы она заняла частное положение относительно плоскостей проекций, которые при этом не меняют своего положения;

б) выбором новой плоскости проекций, по отношению к которой фигура, не имеющая своего положения в пространстве, окажется в частном положении. Первый путь лежит в основе способа плоскопараллельного перемещения, а второй — в основе способа замены плоскостей проекций.

Существует несколько способов плоскопараллельного перемещения:

1. Способ параллельного перемещения. При этом плоскости, по которым двигаются точки фигуры, параллельны плоскости проекций. Траектория — произвольная плоская линия;

2. Способ вращения вокруг оси, перпендикулярной к плоскости проекций. Траектории перемещаемых точек — дуги окружностей, центры которых находятся на оси вращения;

3. Способ вращения вокруг оси параллельной плоскости проекций (вокруг линии уровня).

Это частный случай параллельного перемещения. За траекторию движения точки принимается не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между осью вращения и данной точкой.

При вращении точки вокруг оси перпендикулярной, П 2 , фронтальная проекция точки перемещается по окружности, а горизонтальная — по прямой, перпендикулярной оси вращения. Если же точка вращается вокруг оси, перпендикулярной П 1 , то в горизонтальной плоскости траекторией ее движения будет окружность, а во фронтальной – прямая, перпендикулярная оси вращения. На рисунке 32 показано построение новых проекций точек при помощи способа вращения. На рисунке 32 а – вращение вокруг фронтально-проецирующей оси, на рисунке 32 б – вокруг горизонтально-проецирующей оси.

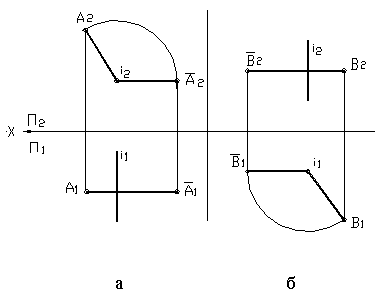
Рисунок 32

Этим способом удобно находить натуральные величины отрезков и фигур, занимающих проецирующее положение.

На рисунке 33 показан пример определения натуральной величины треугольника АВС, плоскость которого перпендикулярна П 2 . За ось вращения необходимо взять фронтально-проецирующую прямую, проходящую через точку, принадлежащую этой плоскости. В данном случае выбрана точка А — вершина треугольника. Плоскость треугольника вращается во фронтальной плоскости вокруг оси до положения, параллельного горизонтальной плоскости. Во фронтальной плоскости точки С и В перемещаются по окружностям, радиус которых равен расстоянию от оси вращения до фронтальных проекций точек. В горизонтальной плоскости траектории движения точек – прямые, перпендикулярные оси. Полученная проекция треугольника А´В´С´, является его натуральной величиной.

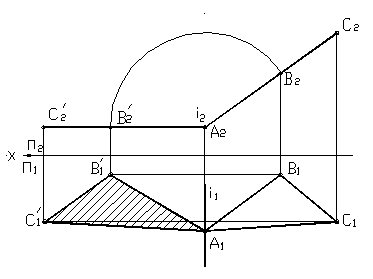
Рисунок 33

Способ вращения наиболее часто применяется при определении натуральных величин сечений поверхностей плоскостями частного положения.

Сущность этого способа состоит в том, что положение фигуры в пространстве не меняется, а вводится новая система плоскостей проекций. Новая плоскость проекции выбирается перпендикулярно к одной из старых. При этом, проецируемая фигура по отношению к новой плоскости занимает частное положение, обеспечивая наиболее удобное решение задачи. Если замена одной плоскости не обеспечивает требуемый результат, то новую плоскость заменяют еще раз.

На рисунке 34 показано построение проекции точки А в новой системе плоскостей проекций при замене плоскости П 1 на П 4 . Плоскость П 4 перпендикулярна П 2 . Проекция точки А1 заменяется на А 4 . По линии связи откладывается расстояние от заменяемой проекции точки до новой оси.

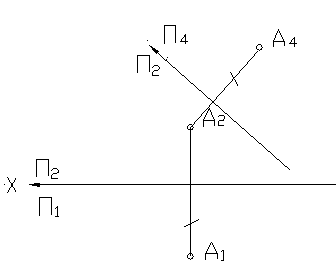
Рисунок 34

На рисунке 35 дан пример определения натуральной величины отрезка общего положения. Новая плоскость П 4 выбирается параллельно одной из проекций отрезка. При этом проекция отрезка на эту плоскость будет являться его натуральной величиной.

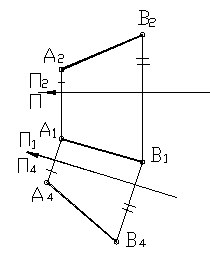
Рисунок 35

В некоторых случаях требуется замена двух плоскостей проекции. Например, при определении расстояния от точки до прямой. При этом прямую необходимо спроецировать в точку. На рисунке 36 отрезок общего положения переведен в проецирующее положение по отношению к плоскости П₅.

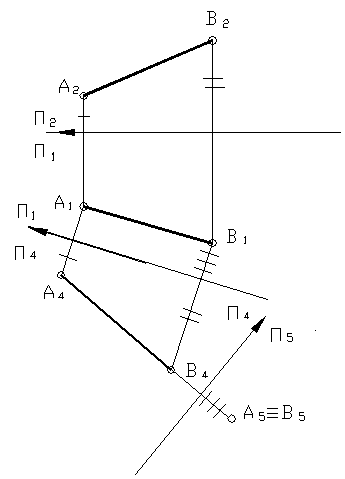
Рисунок 36

1. Назовите, какие вы знаете способы преобразования чертежа. Для чего они применяются?

2. Какие задачи можно решать при помощи способа вращения вокруг проецирующей оси?

3. По каким линиям перемещаются проекции точки при вращении вокруг горизонтально проецирующей оси?

4. Можно ли определить натуральную величину фигуры общего положения способом вращения вокруг проецирующей оси?

5. В чем суть способа замены плоскостей проекций?

6. Как построить проекцию точки в новой системе плоскостей проекций? Этапы построения.

7. Сколько замен нужно осуществить, чтобы перевести отрезок общего положения в проецирующее положение?

8. Как нужно выбрать новую плоскость, для того, чтобы сделать плоскость общего положения проецирующей?

© ФГБОУ ВПО Красноярский государственный аграрный университет

Источник

Метод вращения вокруг оси

Одним из наиболее эффективных методов определения метрических характеристик плоских фигур является вращение вокруг оси, в качестве которой обычно используют линию уровня или проецирующую прямую.

Способ вращения вокруг проецирующей прямой

Перемещение точки при её вращении вокруг проецирующей прямой является частным случаем параллельного перемещения и подчиняется следующим правилам.

1. Траектория движения точки – дуга окружности с центром, расположенным на оси вращения. Радиус окружности равен расстоянию между точкой и осью вращения.
2. При вращении точки вокруг прямой, перпендикулярной фронтальной плоскости проекции, фронтальная проекция точки перемещается по дуге окружности, а горизонтальная – параллельно оси X.
3. При вращении точки вокруг прямой, перпендикулярной горизонтальной плоскости проекции, горизонтальная проекция точки перемещается по дуге окружности, а фронтальная – параллельно оси X.

Руководствуясь рассмотренными правилами, повернем отрезок CD в положение, параллельное фронтальной плоскости проекции. В качестве оси вращения i будем использовать горизонтально проецирующую прямую, проведенную через точку D.

При повороте отрезка положение точки D не изменится, поскольку она лежит на оси i. Точку C’ переместим по дуге окружности радиусом C’D’ в положение C’₁ так, чтобы выполнялось условие C’₁D’₁ || X. Для нахождения точки C»₁ из C» проведем прямую, параллельную оси X, до пересечения её с линией связи, восстановленной из т. C’₁.

На следующем рисунке показан способ перевода отрезка в горизонтально проецирующее положение. Построения выполнены в два этапа и описаны ниже.

Сначала вращением вокруг оси i₁ CD перемещают в положение C₁D₁, параллельное фронтальной плоскости проекции. После этого вращением вокруг оси i₂ отрезок переводится в искомое положение C₂D₂, где он перпендикулярен горизонтальной плоскости проекции.

Расположение осей вращения выбирают исходя из удобства дальнейших построений. В нашей задаче горизонтально проецирующая прямая i₁ проходит через точку D, а проекция i»₂ фронтально проецирующей прямой i₂ лежит на продолжении отрезка C»₁D»₁.

Способ вращения вокруг линии уровня

Действенным и наиболее рациональным приемом решения задач, в которых требуется определить натуральную величину угла, является способ вращения вокруг линии уровня.

Основные правила построения

1. Радиус вращения точки равен расстоянию между точкой и линией уровня, выполняющей роль оси. Натуральную величину радиуса определяют методом прямоугольного треугольника.
2. При вращении вокруг горизонтали h точка перемещается по окружности, которая проецируется на горизонтальную плоскость в отрезок прямой, перпендикулярный горизонтальной проекции горизонтали h’. На фронтальную плоскость окружность, по которой движется точка, проецируется в эллипс. Строить его нет необходимости.
3. При вращении вокруг фронтали f точка перемещается по окружности, которая проецируется на фронтальную плоскость в отрезок прямой, перпендикулярный фронтальной проекции фронтали f». Вместе с тем горизонтальная проекция линии перемещения представляет собой эллипс, строить который не обязательно.

Рассмотрим, как определить действительную величину угла между прямыми a и b, пересекающимися в точке A. Построения представлены на рисунке и выполнены согласно алгоритму, который описан ниже.

1. Проводим фронтальную проекцию h» горизонтали h. Она пересекает прямые a» и b» в точках 1» и 2». Определяем горизонтальные проекции 1′ и 2′ и через них проводим h’.
2. Находим центр вращения O. Его горизонтальная проекция O’ лежит на пересечении прямой h’ с перпендикуляром, проведенным из A’ к h’.
3. Определяем натуральную величину радиуса вращения R = O’A’₀. Для этого строим прямоугольный треугольник O’A’A’₀, катет которого A’A’₀ равен расстоянию от A» до h».
4. Проводим дугу окружности радиусом R до пересечения её с прямой O’A’ в точке A’₁. Соединяем A’₁ с точками 1′ и 2′. Искомый угол ϕ построен.

Источник

Основные задачи, решаемые способом вращения

Задача№1. Преобразовать прямую общего положения во фронтальную прямую уровня (рисунок 1.4.14).

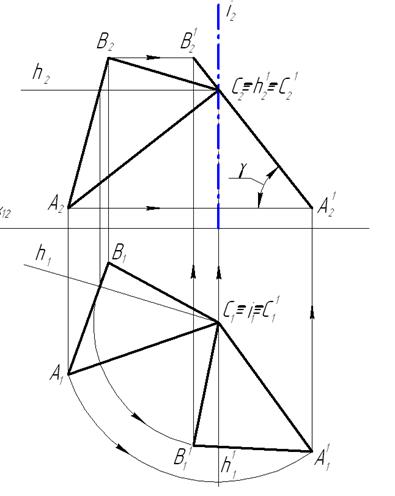
Рассмотрим решение задачи, вращая прямую АВ вокруг горизонтально-проецирующей прямой i₁. Чтобы прямая АВ преобразовалась во фронтальную прямую уровня, необходимо ее повернуть вокруг оси, пока она не примет положение, параллельное фронтальной плоскости проекций. Если заданный отрезок прямой требуется повернуть до положения, параллельного плоскости П₁, то ось вращения следует расположить перпендикулярно П₂, если прямую следует повернуть до положения параллельного П₂, то ось вращения должна быть расположена перпендикулярно к плоскости П₁. Для упрощения графического решения этой задачи горизонтально проецирующую ось вращения i выберем проходящей через точку В. Тогда, при вращении прямой вокруг оси, точка В останется неподвижной (В₁≡В₁ 1 , В₂≡В₂ 1 ), а точка А₁ примет положение А₁ 1 и А₂ 1 . Траектория точки А является часть окружности а, лежащей в плоскости θ, параллельной П₁. Поэтому а₂≡θ₂, а₁ – окружность с центром в i₁, радиус которой равен отрезку А₁В₁. Преобразованная прямая будет являться фронтальной прямой уровня, а отрезок А₂В₂ – его натуральной величиной. Также в задаче определяется натуральная величина угла наклона φ прямой АВ к горизонтальной плоскости проекций.

Рисунок 1.4.14 – Решение первой основной задачи способом вращения

Задача №2. Преобразовать прямую общего положения в горизонтально проецирующую прямую (Рисунок 1.4.15).

Эта задача решается при помощи двух преобразований: сначала прямую АВ преобразуем в прямую уровня (смотри задачу №1), а затем , чтобы прямая была перпендикулярно горизонтальной плоскости проекций, введем новую ось вращения i 1 , перпендикулярную фронтальной плоскости проекций и проходящую через точку А. В этом случае точка А останется неподвижной, а точка В на чертеже примет положение В₂ 11 . Траектория точки В является часть окружности, лежащей в плоскости, параллельной фронтальной плоскости проекций, поэтому в горизонтальной плоскости проекций она совпадет с горизонтальной проекцией преобразованной прямой АВ (А₁ 1 В₁ 1 ). Горизонтальная проекция прямой, после второго преобразования, будет являться точкой А₁ 11 В₁ 11 , т.е. прямая станет горизонтально проецирующей прямой.

Рисунок 1.4.15 — Решение второй основной задачи способом вращения

Задача №3. Преобразовать плоскость общего положения во фронтально проецирующую (рисунок 1.4.16). Плоскость задана ΔABC.

Предварительно в плоскости проводим прямую уровня, в нашем случае – это горизонталь h. Заметим, если плоскость преобразуется в горизонтально проецирующую, то это – фронталь f. Через вершину В треугольника проведем горизонтально проецирующую ось вращения i и вокруг нее будем вращать треугольник до положения, перпендикулярного плоскости П₁. Для этого на чертеже поворачиваем фронтальную проекцию горизонтали h₁ вокруг горизонтальной проекцией оси вращения i₁ так, чтобы она по отношению к оси х располагалась перпендикулярно. При этом форма повернутой горизонтальной проекции треугольника A₁ 1 B₁ 1 C₁ 1 осталась неизменной по отношению к проекции A₁B₁C₁. Так как горизонталь повернулась перпендикулярно фронтальной плоскости проекций, то на эту плоскость она проецируется в точку, а сам треугольник – в виде отрезка прямой A₂ 1 B₂ 1 C₂ 1 . Плоскость треугольника стала фронтально-проецирующей, а угол γ между фронтальной его проекцией и оси х – натуральной величиной угла наклона плоскости ΔABC к горизонтальной плоскости проекций.

Рисунок 1.4.16 — Решение третьей основной задачи способом вращения

Задача №4. Преобразовать плоскость общего положения в горизонтальную плоскость уровня (рисунок 1.4.17).

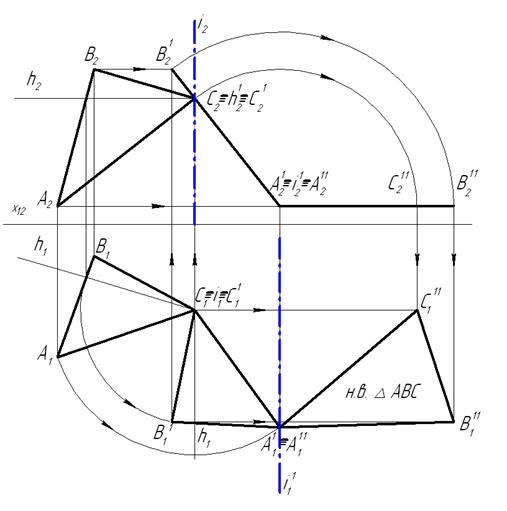
Для решения этой задачи необходимо выполнить два преобразования (вращения): сначала повернуть плоскость, чтобы она стала фронтально проецирующей (смотри задачу №3), а затем, повернув вторично плоскость так, чтобы плоскость располагалась по отношению к горизонтальной плоскости проекций параллельно. Для второго вращения введем еще одну фронтально проецирующую ось вращения i 1 , проходящую через точку А. На чертеже строим новую фронтальную проекцию ΔABC(A₂ 11 B₂ 11 C₂ 11 ), повернутую вокруг i₂ 1 до горизонтального положения. В горизонтальной проекции, в точках пересечения линий связи проекций одноименных точек треугольника, получим положение треугольника в горизонтальной плоскости уровня, а следовательно натуральную величину самого треугольника ABC.

Рисунок 1.4.17 — Решение четвертой основной задачи способом вращения

Построение разверток

Разверткой поверхности называется плоская фигура, образованная последовательным совмещением поверхности с плоскостью без разрывов и складок. При развертывании поверхность рассматривается как плоская, но нерастяжимая. Цель развертывания поверхностей – создание моделей поверхностей из листового материала путем последующего изгибания и «свертывания» их разверток.

Основные свойства разверток:

— прямая на поверхности переходит в прямую на развертке;

— параллельные прямые на поверхности переходят в параллельные прямые на развертке;

— длины отрезка линии на поверхности и той же линии на развертке равны;

— углы между линиями на поверхности и между соответствующими линиями на развертке равны;

— площадь развертки равна площади поверхности;

— все размеры на развертке имеют натуральную величину.

Все поверхности подразделяются на развертываемые и неразвертываемые.

К развертываемым поверхностям относятся:

— гранные поверхности (пирамиды, призмы и т.д.), т.к. плоские элементы многогранника точно совмещаются с плоскостью развертки. В этом случае развертка называется точной.

— линейчатые поверхности (цилиндрические, конические и поверхности с ребром возврата), т.е. это поверхности, у которых смежные образующие-прямые параллельны или пересекаются.

К неразвертывающимся поверхностям относятся все остальные линейчатые, а также нелинейчатые поверхности (цилиндроиды, коноиды, сфера). Развертки этих поверхностей в этом случае называются приближенными или условными.

Источник