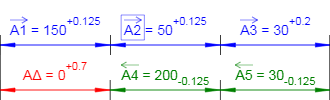4.3.2. Расчет размерных цепей способом равных допусков
Этот способ расчета размерных цепей применяется для решения размерных задач второго типа, т. е. когда при известных номинальных размерах составляющих звеньев и допуску замыкающего звена необходимо определить допуски составляющих звеньев.
Сущность метода заключается в том, на все составляющие звенья размерной цепи назначаются одинаковые допуски
где ТА1, ТА2, …., ТАn – допуски размеров составляющих звеньев размерной цепи;
n – число составляющих звеньев размерной цепи.
Допуск замыкающего звена при этом может быть определен
Полученный средний допуск Аin корректируют для некоторых составляющих звеньев в зависимости от их величины, конструктивных требований и технологических сложностей , возникающих при изготовлении. Но, корректирование должно производиться так, чтобы выполнялось следующее условие n
При корректировке необходимо использовать стандартные допуски и желательно из ряда предпочтительного применения.
Способ равных допусков достаточно прост, но область его применения ограничивается диапазоном размеров. Он может применяться для размерных цепей, в которых размеры составляющих звеньев одного порядка (например, входят в один интервал диаметров) или выполняются с одинаковой экономической точностью. Поэтому данный способ расчета можно рекомендовать только в качестве предварительного назначения допусков.
4.3.3. Расчет размерных цепей способом равной точности
Этот способ иногда называют способом допусков одного квалитета. Он применяется так же, как и способ равных допусков для решения второй задачи. Сущность способа заключается в предположении, что все составляющие звенья размерной цепи могут быть выполнены по какому – либо одному квалитету. Числовые значения допусков составляющих звеньев зависят их номинальных размеров. Требуемый квалитет определяют следующим образом.
Величина допуска любого составляющего размера равна
где i – единица допуска, зависящая от номинального размера;
aj – число единиц допуска, зависящее от квалитета.
Для размеров от 1 до 500 мм единица допуска определяется по формуле
3
i = 0,45 √ D + 0,001D, (4.22)
где D – средний геометрический размер для интервала размеров по ГОСТ 25346 – 89 (СТ СЭВ 145 – 88), в котором находится рассматриваемый размер размерной цепи.
Совместное решение уравнений (4.22) и (4.21) позволяет получить уравнение
T
Известно, допуск замыкающего звена равен сумме допусков составляющих звеньев, Это можно представить в виде уравнения

Из уравнения (4.25) можно определить величину а

Значение единицы допуска для размеров до 500 мм можно выбирать из следующих соотношений
Источник
Способ равных допусков
Составляем сборочную размерную цепь и обозначаем составляющие звенья по часовой стрелке, начиная от исходного звена А ∑ Измерив линейкой с точностью до 1 мм номинальные размеры составляющих звеньев, имеем:
для увеличивающих размеров:
для уменьшающего размера:
для исходного звена: А ∑ =0.
Проведем проверку правильности определения номинальных размеров по основному уравнению размерной цепи:
Зададим предельные размеры исходного звена. Величина зазора определяется номинальными размерами звеньев сборочной размерной цепи и требуемой точностью изготовления сборочной единицы, примем:
Тогда допуск исходного звена равен:
Теперь перейдем непосредственно к расчету сборочной размерной цепи методом максимума-минимума, способом равных допусков.
Средний допуск составляющих звеньев равен:
Т ср = Т ∑ / (m + n) = 700 / (1 + 5) = 700 / 6 = 116,67мкм.
По табл.1 выбираем ближайшие стандартные допуски звеньев в соответствии с их номинальными размерами. При этом необходимо учесть, что звенья А2 и А4 являются стандартными (подшипники качения), их допуски выбираются по соответствующим таблицам для подшипников качения в зависимости от номинального размера ширины кольца подшипника и класса точности (в данном случае принимаем 0 класс точности) и во всех последующих расчетах не подлежат изменению, т.е.
Единицы допуска j, число единиц допуска a и допуски Тi (СТ СЭВ 145-75, СТ СЭВ 177-75)
| Номинальные размеры, мм | Единицы допуска j, мкм | Квалитеты |
| Число единиц допуска а | ||
| Допуски Тi, мкм | ||
| До 3 | 0,55 | |
| Св.3 до 6 | 0,73 | |
| Св.6 до 10 | 0,90 | |
| Св.10 до 18 | 1,03 | |
| Св.18 до 30 | 1,31 | |
| Св.30 до 50 | 1,56 | |
| Св.50 до 80 | 1,86 | |
| Св.80 до 120 | 2,17 | |
| Св.120 до 180 | 2,52 | |
| Св.180 до 250 | 2,89 | |
| Св.250 до 315 | 3,22 | |
| Св.315 до 400 | 3,54 | |
| Св.400 до 500 | 3,89 |
В частности, можно воспользоваться данными табл. 2.
Допуски на ширину кольца подшипника качения, мкм
| Ширина наружного кольца подшипника, мм | Классы точности |
| 0,6 | |
| 0,6-2,5 | |
| 2,5-10 | |
| 10-18 | |
| 18-50 | |
| 50-80 | |
| 80-120 | |
| 120-180 | |
| 180-250 |
Для остальных звеньев определяем допуски по табл.1.
Т 1 = 100 мкм (12 квал);
Т 3 = 110 мкм (11 квал);
Т 5 = 120 мкм (12 квал);
Т 6 = 100 мкм (10 квал);
Проведем проверку выбранных стандартных допусков по выражению:
| (2) |
∑ Т i = 100+120+110+120+120+100 = 670 мкм
что не больше допуска исходного звена Т∑ = 700 мкм, следовательно, условие выполняется.
Таким образом, по выбранным допускам звеньев размерной цепи окончательно определяем предельные отклонения и размеры звеньев. При этом для увеличивающих звеньев поля допусков определяются как для основных отверстий. А для уменьшающих звеньев – как для основных валов. Это правило не относится к подшипникам качения.
На этом расчет размерной цепи методом максимума-минимума, способом равных допусков закончен.
Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет
Источник
Papka_Vz_dlya_bakalavrov_2014g / Папка Вз. Лекции / лекция №15. Решение прямых задач Р.Ц. (мах-мин)
РЕШЕНИЕ ПРЯМЫХ ЗАДАЧ Р.Ц.
Метод полной взаимозаменяемости (метод «МАХ МИН»))
При решении прямых задач замыкающее звено размерной цепи принимается исходным (задаются номинальный размер и предельные отклонения (допуск, поле допуска) замыкающего звена).
Прямую задачу можно решать несколькими способами, из которых чаще применяются:
а) способ равных допусков;
б) способ допусков одного квалитета.
Способ равных допусков применяют с целью предварительной оценки допусков составляющих звеньев. Достоинство этого способа крайняя простота (проще трудно найти). Однако точность расчётов недостаточна, напрямую зависит от количества составляющих размеров и значений их номинальных размеров. Способ позволяет назначить допуски составляющих звеньев для размерных цепей, состоящих из минимального числа этих звеньев (3÷4). При условии, что их размеры находятся в одном интервале номинальных размеров, по ЕСДП одного порядка. В этом случае погрешности расчётов могут быть допустимыми.
При расчётах способом равных допусков условно принимают:
где Tср Аi – средний допуск звена Аi.
Так как допуск замыкающего звена (ТА∆) равен сумме допусков составляющих звеньев, то его можно выразить формулой:
Откуда Tср Ai = 
Полученный средний допуск для каждого составляющего размера, в зависимости от номинального его значения, корректируется до стандартного его значения, приведенного в стандартах ЕСДП (2.3.3) или справочной литературы (1,4 и др.). Корректировку целесообразно проводить с учётом конструктивных требований и технологических возможностей изготовления, при этом необходимо, чтобы не нарушалось условие
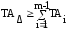
Поля допусков составляющих размеров назначаются исходно из технологических соображений по принципу «допуск в металл», т.е. на охватывающие размеры (отверстия) устанавливают поле допуска «H», не охватываемые (валы) – поле «h», на отдельные линейные размеры – поля «js» или «JS». Принцип «Допуск в металл» облегчает рабочему выполнение размеров по чертежу [3].
Предельные отклонения для увеличивающих звеньев назначают, как для основных отверстий, а для уменьшающих звеньев — как для основных валов.
Способ одного квалитета позволяет решить прямую задачу расчета размерной цепи с большей точностью для большого числа составляющих звеньев, чем при методе равных допусков. Этот метод рекомендуется использовать, если заранее известно, что точность звеньев цепи будет не выше 5-го квалитета (5,6…17,18). Требуемый квалитет для составляющего звена размерной цепи определяют решением следующих уравнений [приложение 1].
Допуск в квалитетах 5-18 определяется по общей формуле
q – номер квалитета;
a – безразмерный коэффициент, установленный для каждого квалитета (таблица 3.1), и не зависящий от номинального размера (называется «a» — число единиц допуска);
i – единица допуска (мкм) –множитель, зависящий от ном. размера.
Источник
Расчет размерных цепей
Прямая задача
Пример решения прямой задачи методом полной взаимозаменяемости
Способ равных допусков
Задание:
Рассчитать заданную размерную цепь (см. рис. 1) по методу полной взаимозаменяемости (max/min).
Допуски на составляющие звенья определять способом равных допусков.
Сделать проверку выполненных расчетов.
Исходные данные:
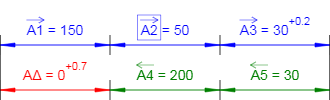
Рисунок 1 — Схема размерной цепи. Исходные данные.
Звенья размерной цепи:
A1 = 150 (мм)
A2 = 50 (мм)
A3 = 30 +0,2 (мм) — звено с известным допуском;
A4 = 200 (мм)
A5 = 30 (мм)
Увеличивающие звенья: A1, A2, A3;
Уменьшающие звенья: A4, A5;
Компенсирующее звено: A2
Замыкающее звено: AΔ
Верхнее отклонение замыкающего звена Es(AΔ) = 0,7 мм
Нижнее отклонение замыкающего звена: Ei(AΔ) = 0 мм
Решение:
1. Определение характеристик замыкающего звена.
1.1. Номинальное значение замыкающего звена
Номинальное значение замыкающего звена AΔ определим по формуле:
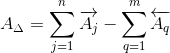 | (1) |
Тогда для заданной размерной цепи формула (1) принимает вид:
AΔ = A1 + A2 + A3 — (A4 + A5)
AΔ = 150 + 50 + 30 — (200 + 30) = 0(мм)
1.2. Допуск замыкающего звена
Допуск замыкающего звена AΔ определим по формуле:
| T(A Δ ) = Es(A Δ ) — Ei(A Δ ) | (2) |
тогда
T(AΔ) = 0,7 — 0 = 0,7(мм)
2. Определение характеристик составляющих звеньев размерной цепи.
2.1. Определение допусков составляющих звеньев
2.1.1 Определение среднего допуска
Средний допуск определим по формуле:
 | (3) |
тогда
| T(Aср) = | 0,7 — 0,2 | = 0,125 (мм) |
| 5 — 1 |
2.1.2 Определение допусков составляющих звеньев с известными отклонениями
Допуски звеньев определяем по формуле (2):
T(A3) = 0,2 — 0 = 0,2(мм);
2.2. Назначение отклонений на звенья размерной цепи
На увеличивающие звенья допуски назначаются в «+», а на уменьшающие звенья допуски назначаются в «-»
A1 = 150 +0,125 (мм);
A4 = 200-0,125 (мм);
A5 = 30-0,125 (мм);
2.3. Определение середины поля допуска i-го звена
Середину поля допуска i-го звена определим по формуле:
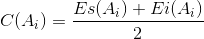 | (4) |
тогда
| С(A1) = | (0,125 + 0) | = 0,0625 |
| 2 |
| С(A3) = | (0,2 + 0) | = 0,1 |
| 2 |
| С(A4) = | (0 + (-0,125)) | = -0,0625 |
| 2 |
| С(A5) = | (0 + (-0,125)) | = -0,0625 |
| 2 |
3. Определение характеристик компенсирующего звена.
Компенсирующее звено: A2 — увеличивающее звено
3.1. Определение допуска компенсирующего звена.
Допуск компенсирующего звена определим по формуле:
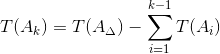 | (5) |
Тогда для заданной размерной цепи формула (5) принимает вид:
T(A2к) = T(AΔ) — (T(A1) + T(A3) + T(A4) + T(A5))
тогда
T(A2к) = 0,7 — (0,125 + 0,2 + 0,125 + 0,125) = 0,125 (мм)
3.2. Определение середины поля допуска компенсирующего звена
Середину поля допуска компенсирующего звена определим по формуле:
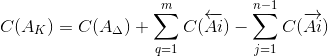 | (6) |
Тогда для заданной размерной цепи формула (6) принимает вид:
C(A2к) = C(AΔ) + (C(A4) + C(A5)) — (C(A1) + C(A3))
тогда
C(A2к) = 0,35 + ((-0,0625) + (-0,0625)) — (0,0625 + 0,1) = 0,0625
3.3. Определение верхнего отклонения компенсирующего звена
Верхнее отклонение компенсирующего звена определим по формуле:
| Es(Ak ) = C(Ak ) + 0,5⋅T(k ) | (7) |
тогда
Es(Aк) = 0,0625 + (0,5⋅0,125) = 0,125
3.4. Определение нижнего отклонения компенсирующего звена
Нижнее отклонение компенсирующего звена определим по формуле:
| Ei(Ak ) = C(Ak ) — 0,5⋅T(k ) | (8) |
тогда
Ei(Aк) = 0,0625 — (0,5⋅0,125) = 0
Звенья размерной цепи с определенными допусками:
A1 = 150 +0,125 (мм);
A2 = 50 +0,125 (мм);
A3 = 30 +0,2 (мм);
A4 = 200-0,125 (мм);
A5 = 30-0,125 (мм);
Рисунок 2 — Схема размерной цепи. Результаты расчета.
Проверка правильности решения задачи производится по формулам:
Верхнее отклонение замыкающего звена Es(AΔ) определим по формуле:
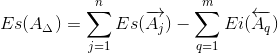 | (9) |
Тогда для заданной размерной цепи формула (9) принимает вид:
Es(AΔ) = Es(A1) + Es(A2) + Es(A3) — (Ei(A4) + Ei(A5))
тогда
Es(AΔ) = 0,125 + 0,125 + 0,2 — ((-0,125) + (-0,125)) = 0,7
Нижнее отклонение замыкающего звена Ei(AΔ) определим по формуле:
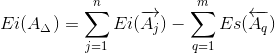 | (10) |
Тогда для заданной размерной цепи формула (10) принимает вид:
Ei(AΔ) = Ei(A1) + Ei(A2) + Ei(A3) — (Es(A4) + Es(A5))
тогда
Ei(AΔ) = 0 + 0 + 0 — (0 + 0) = 0
Источник