Решение задачи схематическим способом это как

Решение задачи схематическим способом это как

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

• Главная
• 9-Класс
• Алгебра
• Видеоурок «Cхематический способ решения текстовых задач»

Существует несколько способов решения текстовых задач:

• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;

• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;

• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;

• схематический способ – это способ решения текстовой задачи с помощью схем;

• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.

Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели. В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи. В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи. В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры. В схематическом способе математической моделью является схема, с помощью которой находят решение задачи. В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.

На этом занятии мы рассмотрим схематический способ решения текстовой задачи. Это старинный приём решения задач. Его знали в Древней Греции ещё до нашей эры во времена Пифагора. А в 18-19 веках нашей эры этот метод успешно использовали купцы при торговле смешанным товаром. Схематический способ предполагает решение текстовой задачи с помощью схемы. Познакомимся с ним на примере следующей задачи.

Задача 1. Родительский комитет детского садика решил закупить конфеты для формирования новогодних подарков для 100 детей. Было решено сделать подарки на сумму 150 рублей каждый. На оптовой базе они выбрали конфеты по цене 225 рублей, 135 рублей и 180 рублей за 1кг. Каждая конфета в среднем весит 10г. Сколько конфет каждого вида необходимо купить родительскому комитету?

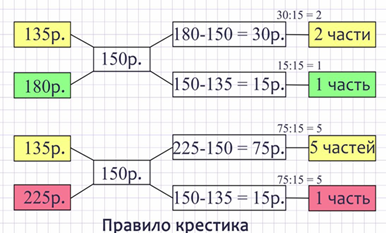
Решим задачу схематическим способом Леонтия Филипповича Магницкого для трёх веществ. Математик Магницкий — автор первого в России учебного справочника по математике. Запишем в столбик друг под другом цены двух сортов конфет в порядке возрастания 135руб и 180руб. В центре второго столбика рядом запишем цену смеси конфет 150руб. В третьем столбце сверху запишем разность 180 и 150, а ниже разность 150 и 135.

Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 150-ти, то есть 30руб и 15руб, Разделим эти числа на их наибольший общий делитель – на 15, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 2части и 1часть. Теперь аналогичную операцию проделаем с конфетами по цене 135руб и 225руб. В центре второго столбика рядом запишем цену смеси конфет 150руб. В третьем столбце сверху запишем разность 225 и 150, а ниже разность 150 и 135. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 150-ти, то есть 75руб и 15руб, Разделим эти числа на их наибольший общий делитель – на 15, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 5частей и 1часть. Мы получили две схемы, в которых результаты разностей чисел мы записывали крестиком относительно стоимости смеси 150рублей. Именно поэтому этот способ по-другому называется «правилом крестика». Числа четвёртых столбцов схем показывают долю конфет соответствующей цены от общего количества конфет в подарке по цене 150рублей за 1кг. Из схемы видно, что в смеси на конфеты по цене 135руб приходится 2 + 5частей, то есть 7частей, а на конфеты по цене 180руб и 225руб приходится по 1части. Это означает, что если на 100детей распределить по 1конфете массой 10г, то потребуется 1кг конфет по 180руб и 1кг по 225руб. Конфет по цене 135руб должно быть в 7 раза больше, значит, нужно закупить 7кг конфет по этой цене.

Схематический способ решения текстовых задач значительно упрощает решение задач на смешивание растворов и получение сплавов определённого долевого или процентного состава. Рассмотрим следующую задачу.

У хозяйки имеются 70%-ная уксусная эссенция и 6%-ный раствор пищевого уксуса, купленные в магазине. Для консервирования ей нужен 14%-ный раствор уксуса. Как хозяйке получить необходимый раствор?

Запишем в столбик друг под другом проценты смешиваемых растворов в порядке возрастания 6% и 70%. В центре второго столбика рядом запишем процент нового раствора 14%. В третьем столбце сверху вниз запишем разность числа последней строки и 14, а затем разность 14 и числа первой строки. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 14-ти, то есть 56% и 8%. Разделим эти числа на их наибольший общий делитель – на 8, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 7 и 1. Эти числа определяют долю раствора соответствующей концентрации от общего количества раствора. Таким образом, чтобы получить

14 % – ный раствор уксуса, надо смешать одну часть эссенции и 7 частей пищевого уксуса. В роли одной части может выступать любой объём. Хозяйка пипеткой может взять 1 каплю эссенции и 7капель уксуса, если ей нужен небольшой объём. Для объёма побольше можно взять, например, чайную ложку эссенции и 7чайных ложек уксуса.

Разберём решение ещё одной задачи на сплавы схематическим способом.

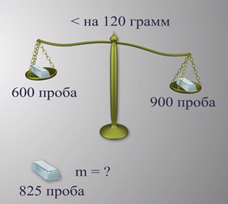
Масса одного куска серебра 600-й пробы отличается от массы куска серебра 900-й пробы на 120 граммов. Определить массу слитка из этих кусков, если его проба стала равна 825.

Запишем в столбик друг под другом пробы кусков серебра в порядке возрастания 600 и 900. В центре второго столбика рядом запишем пробу нового сплава из этих кусков 825. В третьем столбце сверху вниз запишем разность числа последней строки и 825, а затем разность 825 и числа первой строки. Таким образом, в третьем столбце сверху вниз записаны результаты модуля разности чисел первого столбца и 825-ти, то есть 75 и 225. Разделим эти числа на их наибольший общий делитель – на 75, а результаты запишем в четвёртый столбик соответственно их строкам сверху вниз. Получился столбец с числами 1 и 3. Эти числа определяют долю куска серебра соответствующей пробы от общей массы сплава из кусков серебра 600-й и 900-й пробы. По условию задачи массы кусков серебра отличаются друг от друга на 120 г. Из схемы видно,куски отличаются друг от друга на 2 части, следовательно, на 1 часть приходится 120:2 г, то есть 60 г. Главный вопрос задачи: определить массу слитка из кусков серебра. Из схемы видно, что на весь сплав приходится 4 части. Нетрудно понять, что вся масса слитка в 2 раза больше разности масс двух кусков серебра, значит, вся масса слитка будет составлять 2 умноженное на 120 г или 4 умноженное на 60 г, то есть 240 г.

Таким образом, из приведённых примеров различных задач можно сделать вывод, что схематический способ решения текстовых задач значительно упрощает их решение. Недостатком этого метода является ограниченность его применения. Таким способом можно решать только задачи на смешивание сыпучих материалов, на разбавление растворов или на сплавы металлов.

Источник

Несколько способов решения одной задачи

Муниципальное бюджетное образовательное учреждение

средняя общеобразовательная школа № 91

с углубленным изучением отдельных предметов

Ленинского района г. Н.Новгорода

Научное общество учащихся

Несколько способов решения одной задачи.

Выполнила: Куракина Елена

ученица 7п класса

ГЛАВА 1 Задачи и их решение 4

1.1 Составные части задачи 4

1.2. Схематическая запись задач 5

1.3. Сущность и структура решения математической задачи 6

ГЛАВА 2 Несколько способов решения одной задачи 8

2.1 Способ 1 (арифметический) 8

2.2 Способ 2 (графический) 9

2.3 Способ 3 (вычислительный) 10

2.4 Способ 4 (алгебраический) 11

ГЛАВА 3 Методы решения геометрических задач. 14

3.1 Пример решения геометрической задачи 15

ГЛАВА 4 Варианты решения текстовых задач 19

4.1 Решение задач с помощью уравнений 19

4.2 Задача на среднюю скорость 22

ГЛАВА 5 Стратегии решения задач 24

5.1 Выбор наилучшей стратегии 28

Список использованных источников и литературы 31

«Математика ум в порядок приводит»- эти слова принадлежат великому . Что же он имел в виду?

Дело в том, что одним из наиболее важных качеств мышления является его логичность, способность делать из правильных посылок (суждений, утверждений) правильные выводы, находить правильные следствия из имеющихся фактов.

О человеке, у которого хорошо развито логическое мышление, говорят, что он основательно мыслит, дисциплинированно рассуждает.

И вот оказывается, что это ценнейшее качество возникает и развивается главным образом в процессе изучения математики, в частности, в процессе решения математических задач. Ведь математика это практическая логика, в ней каждое новое положение получается с помощью строго обоснованных рассуждений на основе ранее известных положений, то есть строго доказывается. Ломоносов приведёнными выше словами подчеркнул именно эту особенность математики.

Изучение математики формирует не только логическое мышление, но и много других качеств человека: сообразительность, настойчивость, аккуратность, критичность и др.

Очень важным среди них является пространственное воображение, умение представить в уме (вообразить) какие-то предметы, фигуры и при этом увидеть их не только неподвижными, но и в изменении,- представить, что произойдёт, если их как-то переместить, повернуть и т. д. При изучении математики, в особенности при решении геометрических задач всё время приходится делать это, и тем самым постепенно развивается эта важная способность.

Эта же способность представить в уме — вообразить — важна и для планирования своей работы, своих действий с тем, чтобы они были наиболее разумными, рациональными и безошибочными.

Изучение математики, решение математических задач развивают, помимо пространственного воображения, и способность догадываться, угадывать заранее результат, способность разумно искать правильный путь в самых запутанных условиях.

Прочтя задачу и ещё не производя ни каких действий, нужно стремиться к тому, чтобы научиться сразу видеть, что тот или иной способ непригоден для её решения, а вот какой-то другой способ может быть использован. Такое умение вырабатывается в процессе решения одной и той же задачи разными способами. Именно поэтому часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи.

Решая одну и ту же задачу различными методами, можно лучше понять специфику того или иного метода, его преимущество и недостатки в зависимости от содержания задачи.

Нередко найденный способ решения может быть в дальнейшем использован для решения более трудных задач, сходных с решённой задачей.

Отметим ещё, что решение задач, допускающих ряд решений,- увлекательная работа, требующая знания всех разделов школьной математики.

Цель работы – показать многообразие подходов при решении одной задачи.

ГЛАВА 1 Задачи и их решение

1.1 Составные части задачи

Задача представляет собой требование или вопрос, на который надо найти ответ, учитывая те условия, которые указаны в задаче. Поэтому приступая к решению какой-либо задачи, надо её внимательно изучить, установить, в чем состоят её требования (вопросы), каковы условия, исходя из которых надо решить задачу. Все это называется анализом задачи.

Первое, что мы можем заметить при чтении задачи: в ней имеются утверждения и требования. Утверждения – условия задачи, требования формулируются в виде вопроса. Поэтому первое, что нужно сделать при анализе задачи,- это расчленить формулировку задачи на условия и требования. Глубина анализа зависит главным образом от того, знакомы ли мы с видом задач, к которому принадлежит заданная, и знакомы ли с общим способом решения этих задач. Если да, то нам достаточен простейший анализ, сводящийся к установлению вида данной задачи; если нет, то для нахождения решения задачи нужен более глубокий анализ.

Виды задач, решаемых в курсе математике

1.2 Схематическая запись задач

Результаты предварительного анализа задач надо как-то зафиксировать, записать. Словесная форма записи мало удобна. Более компактной и в тоже время достаточно наглядной формой записи результатов анализа задач является схематическая запись задачи.

Но не для всякой задачи надо делать схематическую запись. Для задач, которые записаны на символическом языке (с помощью общепринятых обозначений и символов) схематическая запись не нужна.

Отличительной особенностью схематической записи задач является широкое использование в ней разного рода обозначений, символов, букв, рисунков, чертежей и т. д. Второй особенностью является то, что в ней четко выделены все условия и требования задачи, а в записи каждого условия указаны объекты и их характеристики, наконец, в схематической записи фиксируется лишь только то, что необходимо для решения задачи; все другие подробности, имеющиеся в задаче, при схематической записи отбрасываются.

1.3 Сущность и структура решения математической задачи

Решить математическую задачу – это значит найти такую последовательность общих положений математики (определений, аксиом, теорем, правил, законов, формул), применяя которые к условиям задачи или к их следствиям (промежуточным результатам решения), получаем то, что требуется в задаче, — её ответ.

Из каких же этапов состоит процесс решения задачи?

Анализ задачи составляет первый этап процесса решения задачи. Построение схематической записи задач составляет второй этап процесса решения. Поиск способа решения задачи – третий этап процесса. Когда способ решения задачи найден, его нужно осуществить, — это будет уже четвертый этап процесса решения – этап осуществления решения. Далее необходимо убедиться, что это решение правильное, что оно удовлетворяет всем требованиям задачи. Для этого производят проверку решения, что составляет пятый этап процесса решения.

При решении многих задач, кроме проверки, необходимо ещё произвести исследование задачи, а именно, установить, при каких условиях задача имеет решение и при том сколько различных решений в каждом отдельном случае; при каких условиях задача вообще не имеет решения и т. д. Всё это составляет шестой этап процесса решения.

Убедившись в правильности решения, необходимо четко сформулировать ответ задачи, — это будет седьмой этап.

Наконец, в учебных и познавательных целях полезно также произвести анализ выполненного решения, в частности установить, нет ли другого, более рационального способа решения, нельзя ли задачу обобщить, какие выводы можно сделать из этого решения и т. д. Все это составляет последний, конечно не обязательный, восьмой этап решения.

ГЛАВА 2 Несколько способов решения одной задачи

Для развития логической деятельности учащихся, особенно в 7-х классах, представляется целесообразным показать, что та или иная задача может быть решена несколькими способами; при этом один вариант решения обычный, а другой специфичный, основанный на той иди иной особенности данного условия – он изящнее, но требует сообразительности.

В качестве примера рассмотрим решение задачи несколькими способами.

Задача: Чтобы доставить письмо за 2 ч. 40 мин. из А в В, расстояние между которыми 70,5 км, почтальон ехал сначала на велосипеде со скоростью 12,75 км/ч, а затем на мотоцикле со скоростью 67,5 км/ч. Сколько времени ехал почтальон на велосипеде и сколько на мотоцикле?

2.1 Способ 1 (арифметический)

70,5 км

A Vв=12,75 км/ч Vм=67,5 км/ч В

Дополнительная работа: вводим обозначения

Vв=12,75 км/ч= 12 км/ч

Vм=67,5 км/ч= 67 км/ч

S=70,5 км = 70 км

t0=2 ч 40 мин=2 ч tв =? tм=?

1. Sв=Vв*t0= 12 * 2 = 34 (км) –проехал бы почтальон, если бы все 2ч 40 мин ехал на велосипеде

2. Sм= S0-Sв=70 — 34 = 36 (км) – расстояние, которое осталось бы проехать на мотоцикле

3. Vм – Vв = 6712 = 54 (км/ч) – разность скоростей

4. tм = Sм : Vр = 36 : 54 = (ч) – ехал на мотоцикле

5. tв= 2 — = 2 (ч) – ехал на велосипеде

Ответ: tв=2 ч; tм= ч.

2.2 Способ 2 (графический)

Дополнительная работа: зададим формулы движения почтальона

(у=ах+в), так как график проходит через точку (2; 70,5) следовательно

70,5= 67,5 * 2+ в

70,5= 67 *2

Находим точку пересечения графиков. Точка пересечения графиков находится решением системы уравнений: t=2, S= 25,5 – точка Е

Ответ: tв=2 ч; tм=2 — 2 = ч.

2.3 Способ 3 (вычислительный)

Ot – ось времени, OV – ось скорости

Путь, пройденный почтальоном, можно представить в виде суммы площадей прямоугольников S1 и S2 или площадью прямоугольника со стороной 67,5 и без площади прямоугольника S3, то есть.

S = V * t аналогия, то есть путь можно рассмотреть как

S = a * b площадь прямоугольника

Имеем: S1 +S2 = S=70.5 (км) – по условию

S = 67.5 * 2 – S3; S3 =(67.5 – 12.75)*t

67 * 2 – (67.5-12.75) * t = 70.5

t — время затраченное почтальоном на движение на велосипеде

tм =2 — 2 = ч. – время, затраченное на движение на мотоцикле.

2.4 Способ 4 (алгебраический)

Алгебраический способ решения задачи — это прежде всего условие задачи переводят на язык математики. Основа такого перевода, его первый шаг – введение буквы для обозначения какой-либо неизвестной величины. В результате перевода обычно получается равенство, содержащее букву. Это равенство называют уравнением. Следовательно алгебраический способ –это способ решения задач с помощью уравнений

На данном способе я хочу остановиться более подробно, так как он рассматривается в школьном курсе математики и является базовым уровнем.

1. Работа над задачей: выделение условия и требования (вопрос задачи)

2. Что является объектом задачи? (Движение почтальона на велосипеде и мотоцикле)

3. Следовательно, данная задача относится к типу задач на движение

4. Основная формула движения S=V*t; S, V, t.

Использование анализа и синтеза при решении задачи: разбиение основной задачи на подзадачи.

а) какой вопрос задачи.

Найти время движения почтальона на велосипеде и на мотоцикле.

t= 2 ч (общее)

tв + tм

Vв Sв + Sм Vм

12 км/ч 70,5 км 67 км/ч

Из данного графа видно, что нам неизвестно и какие условия необходимы для решения задачи.

1) Sв + Sм =70,5 — модель уравнения

2) tв + tм =2 — модель уравнения

1) 12 * х + 67 ( 2 — х) = 70,5

12 (2 — х) +67*х = 70,5

2)

Данный способ дает сразу четыре уравнения. Поэтому здесь можно проявить творчество, самостоятельность.

Построение графа к поиску решения дает наглядное представление, повторение формул движения.

Граф – это схема поиска решения задачи, руководствуясь которой ученик постоянно анализирует задачу.

1. Чтобы ответить на вопрос я должен знать расстояние движения на велосипеде, расстояние движения на мотоцикле.

2. Если я буду знать расстояние, то могу ответить на вопрос задачи.

Способов решения задачи гораздо больше, чем я смогла представить в этой работе. Какие-то способы мне нравятся, какие-то не очень.

При решении данной задачи я показала четыре способа решения одной задачи.

1. Арифметический – данный способ я считаю не рациональным, так как очень часто сложно объяснить, сделать пояснение к действиям.

2. Графический способ – является интересным, познавательным, но требует расширенного кругозора по математике.

3. Вычислительный способ является с уклоном геометрических знаний, также учащиеся повторяют систему координат, понятие площади. То есть движение можно рассматривать как площадь прямоугольника. Учащиеся проводят аналогию формулы движения и нахождения площади прямоугольника.

4. Алгебраический способ – это традиционный, рассматриваемый во всех школьных учебниках, и является базовым уровнем. То есть ученик обязан решить задачу с помощью уравнения. Поэтому в своей работе я рассмотрела данный способ более подробно.

Решение задачи с помощью графа это схематический поиск решения задачи. Здесь мне нравится вариативность, ученики могут составить четыре уравнения, с помощью которых ответить на вопрос задачи. Также ученики могут выбрать для себя более подходящий вариант решения, составляется модель уравнения. Я считаю, здесь идет постоянное осмысливание, анализирование задачи.

ГЛАВА 3 Методы решения геометрических задач.

Говоря о поисках решения геометрической задачи, приходится иметь ввиду, что существуют различные методы её решения. Поэтому поиски прежде всего следует направить на выбор конкретного метода. Условно можно разбить на следующие группы:

Связан с использованием соотношений в треугольнике и круге, признаками равенства и подобия и др. Часто приходится проводить дополнительные построения, например, описанные окружности.

2. Метод геометрических преобразований.

Связан с применением преобразований плоскости и пространства (параллельный перенос, симметрия, гомотетия и т. п.).

Связан с использованием векторов, в частности скалярного и векторного произведений.

4. Тригонометрический метод.

Использует применение тригонометрии, теорем синусов и косинусов.

5. Переформулировка задачи.

Замена задачи другой, эквивалентной данной.

Перечисленные методы могут пересекаться, в одном решении может применяться несколько методов. Например, можно заменить исходную задачу другой, которую решают с помощью векторов и преобразований.

При решении геометрических задач полезно показать, что рассматриваемую задачу можно решить различными методами, и если один способ не приводит к цели или слишком громоздок, то лучше обратиться к другому. «Лучше решить одну задачу несколькими методами, чем несколько задач — одним» (Д. Пойя).

3.1 Пример решения геометрической задачи

Задача на тему: «Свойство биссектрисы внутреннего угла треугольника»

Биссектриса BD внутреннего угла треугольника ABC делит противоположную сторону на отрезки, пропорциональные сторонам BC и BA треугольника.

Доказательство 1. (рис. 1)

Проведем через вершину С прямую CM, параллельную биссектрисе ВК, до пересечения в точке М с продолжением стороны АВ. Т. к. ВК – биссектриса угла АВ, то АВК = КВС. АВК = ВМС, как соответственные углы при параллельных прямых ВК и СМ и секущей АМ, и КВС = ВСМ, как накрест лежащие углы при параллельных прямых ВК и СМ и секущей ВС. Поэтому ΔВМС равнобедренный с основанием СМ, значит, ВС=ВМ. По теореме о параллельных прямых, пересекающих стороны угла, имеем АК:КС = АВ:ВМ, а ввиду ВМ=ВС получим АК:КС = АВ:ВС, т. е. АВ:АК = ВС:КС.

Рис.1 Применение теоремы о параллельных прямых, пересекающих стороны угла

Доказательство 2. (рис. 2)

ΔКРС (С — общий, ВАС = РКС – соответственные при параллельных прямых КР и АВ и секущей АС). Из подобия этих треугольников следует, что .

АВК = СВК (ВК – биссектриса),

АВК = РКВ ( накрест лежащие при параллельных прямых КР и АС и секущей ВК), значит, СВК = РКВ, следовательно, ΔBКР – равнобедренный с основанием ВК, т. е. ВР = КР. Учитывая это равенство, получаем , .

Т. к. параллельные прямые отсекают на сторонах угла пропорциональные отрезки, то . Таким образом, имеем , т. е. .

Рис.2 Применение теоремы о параллельных прямых, пересекающих стороны угла

Доказательство 3. (рис. 1)

Проведем через точку С прямую СМ, параллельную биссектрисе BК, до пересечения в точке М с продолжением стороны АВ. ΔАВК

ΔАМС (А – общий, АВК = АМС). Следовательно, , но АМ = АВ+ВМ и т. к. ВМ = ВС, то АМ = АВ+ВС. АС = АК+КС, значит, , или 1 + , откуда , т. е. .

Доказательство 4. (рис. 3)

Опустим перпендикуляры АЕ и CF из вершин А и С на прямую ВК. Прямоугольные треугольники АВЕ и ВСF подобны, т. к. они имеют равные острые углы при вершине В. Из подобия этих треугольников следует пропорциональность сторон: .

Прямоугольные треугольники АЕК и СFK тоже подобны. У них углы при вершине К равны как вертикальные. Из подобия этих треугольников следует пропорциональность сторон

. Сравнивая это равенство с предыдущим, получим , т. е. .

Рис.3 Применение метода подобия

Доказательство 5. (рис. 4)

Имеем . С другой стороны, , где BN – высота, проведенная из вершины В. Из этих равенств получаем: , т. е. .

Рис.4 Применение тригонометрии и метода площадей

Доказательство 6. (рис. 4)

Треугольники ABК и CВК имеют общую высоту BN, поэтому по следствию из теоремы о площади треугольника . С другой стороны, эти же треугольники имеют по равному углу (), поэтому по теореме об отношении площадей треугольников, имеющих равные углы, имеем: . Из двух равенств для отношения площадей получаем , или .

Доказательство 7. (рис. 4)

По теореме синусов

и , или

и откуда

, или

.

sin A = ( ΔABN), sin С = ( ΔСBN).

Поэтому , т. е. .

Доказательство 8. (рис. 5)

Выполнив осевую симметрию треугольника ABC относительно прямой BD.

Т. к. CC1 ВD и AA1 ВD, то CC1 ║ AA1

Δ A1КА (КAA1=КСC1 – накрест лежащие при параллельных прямых СC1 и AA1 и секущей АС, AКA1=СКC1 – вертикальные). Из подобия этих треугольников следует, что *.

Δ A1АВ (В – общий, ВAA1 = ВC1С – соответственные при параллельных прямых CC1 и AA1 и секущей АВ). Из подобия этих треугольников следует, что

, но АВ= A1В, поэтому **. Из равенств * и ** получаем , т. е. .

Рис.5 Применение метода симметрии

К рассмотрению методов решения геометрических задач полезно будет вернуться в старших классах.

ГЛАВА 4 Варианты решения текстовых задач

4.1 «Решение задач с помощью уравнений»

Задача про фазанов и кроликов

“В клетке находятся фазаны и кролики. Известно, что у них 35 голов и 94 ноги. Узнайте число фазанов и число кроликов.

1. Арифметический способ решения задачи.

Решение задачи.

1) Представим, что на верх клетки, в которых сидят фазаны и кролики, положили морковку. Все кролики встанут на задние лапки, чтобы дотянуться до морковки. Сколько ног в этот момент будет стоять на земле?

35·2=70(ног).

2)Но в условии даны 94ноги. Где же остальные? Остальные не посчитаны – это передние лапки кроликов. Сколько их?

94-70=24(лапки).

3)Сколько же кроликов?

24:2=12(кроликов).

4) А сколько фазанов?

35-12=23(фазана).

Ответ: 23фазана и 12 кроликов в клетке.

Так задача решается в пятом классе, но теперь мы уже умеем решать задачи с помощью уравнений. Так давайте попробуем применить этот способ решения к нашей задаче.

2. Решение задачи с помощью уравнений.

Во-первых, давайте определимся, что мы можем взять за x в этой задаче.

Число фазанов или число кроликов.

Давайте возьмем за x сначала число фазанов, и решим задачу с помощью уравнения.

Решение задачи.

1)Пусть x фазанов в клетке. Тогда кроликов в клетке 35-x. Всего у фазанов 2x ног, а у кроликов 4·(35-x) ног. Зная, что всего у них 94 ноги составим уравнение:

2x+ 4·(35-x) =94

2x+140-4x=94

2x=46

X=23

23фазана в клетке

2) 35-23=12(кроликов) в клетке.

Ответ:23фазана и 12 кроликов в клетке.

Решая эту задачу, мы принимали за x число фазанов, но можно взять за x и число кроликов. Решим эту задачу, взяв за x число кроликов. Решение будет аналогично.

Решение задачи.

1) Пусть x кроликов в клетке. Тогда фазанов в клетке 35-x. Всего у фазанов 2(35-x) ног, а у кроликов 4x ног. Зная, что всего у них 94 ноги составим уравнение:

4x+ 2·(35-x) =94

2x+70=94

2x=24

X=12

12 кроликов в клетке

2) 35-12=23(фазана) в клетке.

Ответ: 23фазана и 12 кроликов в клетке.

Давайте возьмем за x количество ног у всех фазанов и попробуем решить эту задачу.

Решение задачи

1)Пусть у фазанов x ног, тогда у кроликов 94-x ног. Т. к. у каждого фазана по 2 ноги, то у x фазанов x:2 ног, а кроликов по 4 ноги, значит их (94-x):4. Зная, что в клетке всего 35 фазанов и кроликов составим уравнение:

x:2+ (94-x):4=35 |·4

2x+94-x=140

X=140-94

X=46

46 ног у фазанов.

2) 46:2=23(фазана) в клетке.

3)35-23=12(кроликов)в клетке.

Ответ: 23 фазана и 12 кроликов в клетке.

Ну, а теперь примем за x число ног у кроликов и решите эту задачу самостоятельно.

Решение задачи.

1)Пусть у кроликов x ног, тогда у фазанов 94-x ног. Т. к. у каждого фазана по 2 ноги, то у (94-x) фазанов (94-x):2 ног, а кроликов по 4 ноги, значит их x:4. Зная, что в клетке всего 35 фазанов и кроликов составим уравнение:

x:4+ (94-x):2=35 |·4

x+188-2x=140

X=48

48 ног у кроликов.

2) 48:4=12(кроликов) в клетке.

3)35-12=23(фазана)в клетке.

Ответ: 23 фазана и 12 кроликов в клетке.

Мы рассмотрели 4 способа решения задачи про фазанов и кроликов с помощью уравнений, вспомнили арифметический способ, но есть и еще способ, который мы можем применять в 7 классе. Давайте рассмотрим этот способ.

3. Решение задачи с помощью системы уравнений.

Решение задачи

Пусть x кроликов и y фазанов было в клетке. Зная, что их всего 35, составим первое уравнение системы:

x+y=35.

Зная, что у каждого кролика 4 ноги, а у каждого фазана 2ноги, а всего их 94, составим второе уравнение системы: 4x+2y=94

Объединим уравнения в систему и решим её:

Ответ: 23 фазана и 12 кроликов в клетке.

4.2 Задача на среднюю скорость

Задача. Автомобиль ехал из села в город со скоростью 40 км / ч. Какова средняя скорость автомобиля?

I способ

Приняв расстояние от села до города за условную единицу, определим время движения автомобиля в город по формуле t1=S/v1=1/60 (часов условно) и время движения автомобиля из города t2= S/v2= 1/40 (часов условно). Тогда средняя скорость будет равна Vср. = (2*S)/ t1+t2= 2*1/(1/60+1/40)=2*1*120/(2+3)= 48(км/ч)

Ответ: 48км/ч.

II способ

За условное расстояние между селом и городом удобно взять число, кратное 40 и 60, например, 120, 240, 360 и т. д., которые делятся нацело на данные числа.

1.Примем расстояние от села до города равным 240 км.

2.Найдём время движения автомобиля в город и обратно:

t1= S/v1= 240/60= 4(ч);

t2= S/v2= 240/40= 6(ч).

1. Общее время движения автомобиля:

4+6=10(ч).

За это время пройдено расстояние

2*S=2*240= 480(км).

2. Найдём среднюю скорость автомобиля:

vср= 2*S/ t = 480/ 10= 48(км/ч).

Ответ: 48 км/ч.

ГЛАВА 5 Стратегии решения задач

Существует несколько стратегий, которые при правильном использовании могут помочь вам генерировать решения. Несмотря на то, что ни одна единичная стратегия не может гарантировать универсальных решений на все случаи жизни, умение применять эти стратегии придаст направленность и уверенность вашим действиям при решении новых задач.

Приведенные ниже стратегии или руководства по решению задач можно рассматривать как способы планирования решения.

1. Анализ целей и средств. Чаще всего продвижение к цели идет не по прямой дороге. Если цель не может быть достигнута сразу, нередко приходится идти обходными путями или разбивать задачу на более мелкие части — так называемые подзадачи, каждая из которых имеет свою цель, или подцель.

Анализ целей и средств является одним из основных, очень мощных средств решения задач. Сначала задача делится на подцели. Затем человек начинает действовать, чтобы достигнуть определенной подцели. Таким образом, с каждой отдельной победой он будет все ближе и ближе подходить к главной цели.

2. Решение с конца. Анализ целей и средств является примером прямой стратегии — все планируемые действия ориентированы на приближение к подцели и, в конечном итоге, к основной цели. Иногда полезнее оказывается стратегия планирования операций решения с конца, которые обеспечивают движение от конечной цели назад — к текущему или исходному положению.

Простейшим примером такой стратегии может служить игра в обожаемые детьми лабиринты, нарисованные на бумаге, которые нужно проходить с помощью карандаша. Многие из этих лабиринтов содержат несколько возможных путей, отходящих от начальной точки, и среди них только один верный путь, который приведет в конец лабиринта к заветной цели. Даже дети понимают, что они смогут ускорить решение такой задачки-лабиринта, если пойдут в обратном направлении, начав движение с конечной точки и прорисовывая путь к началу лабиринта.

Стратегия решения с конца очень удобна, если от конечной цели ведет меньше путей, чем из исходного положения. Рассмотрим такую задачу: «Площадь, которую покрывают водяные лилии на одном из озер, удваивается каждые двадцать четыре часа. С того момента, как появилась первая лилия, до того, когда лилии полностью покрыли поверхность озера, прошло шестьдесят дней. Когда озеро было покрыто наполовину?». Единственным путем решения этой задачи является применение стратегии решения с конца. Можете ли вы решить ее, пользуясь этой подсказкой? Если озеро полностью было покрыто лилиями на 60-й день, а площадь, которую покрывают лилии, удваивалась каждые сутки, какая часть озера была закрыта в 59-й день? Ответ: половина. Таким образом, пользуясь обратным ходом, мы легко решили эту задачу. Прямая стратегия решения этой задачи наверняка завела бы нас в тупик.

3. Упрощение. Задачи, вызывающие затруднения при решении, чаще всего сложны по структуре. Хороший способ справиться с такой задачей — это упростить ее настолько, насколько возможно, Нередко удачно выбранная форма наглядного представления задачи сама способствует ее упрощению, поскольку позволяет «увидеть» эффективный путь решения.

Предположим, вы столкнулись с классической задачей «кошка на дереве». Предположим, вам надо снять кошку с ветки, расположенной на высоте 3 метров. В вашем распоряжении имеется единственная лестница длиной 2 метра. Для того чтобы лестница была надежно установлена, ее основание должно находиться на расстоянии 1 метра от ствола. Дотянетесь ли вы до кошки?

Лучший путь к решению этой (и не только этой) задачи — графически изобразить исходные данные. Как только информация представлена в виде чертежа, ее можно воспринимать как простую геометрическую задачу: найти гипотенузу прямоугольного треугольника, если его катеты равны 3 и 1 метру.

Формула для нахождения гипотенузы треугольника имеет вид:

Упрощение является хорошей стратегией для решения абстрактных задач, сложных или содержащих информацию, не относящуюся к поиску решения, а эффективное наглядное представление может существенно упростить задачу.

4. Случайный поиск и метод проб и ошибок. Если задача имеет небольшое число возможных путей решения, то случайный поиск приведет к цели в кратчайший срок. Совершенно случайный поиск означал бы отсутствие систематического порядка рассмотрения вариантов и возможность повтора уже рассмотренных решений. Поэтому более предпочтительной стратегией является систематический поиск методом проб и ошибок по всему пространству задачи (содержащему пути решения, цель и исходное положение). Лучше всего применять метод проб и ошибок к решению четко поставленных задач, имеющих конечное число возможных путей решения.

Обе стратегии — метод проб и ошибок и случайный поиск — плохо работают, когда возрастает количество путей решения задачи из-за роста числа возможных комбинаций. Часто бывает полезным разбить задачу на части и воспользоваться методом проб и ошибок для решения более мелких подзадач.

5. Правила. Некоторые типы задач строятся по определенным правилам — например, задачи на последовательности. Как только будут установлены принципы построения такой задачи, можно считать ее решенной. Хороший способ обнаружить заложенную в задаче закономерность — это попробовать отыскать повторяющиеся фрагменты в данных или подцелях.

6. Подсказки. Подсказки — это дополнительная информация, которая сообщается человеку после того, как он начал работать над задачей. Часто подсказка содержит важные дополнительные сведения, необходимые для принятия решения. Иногда она может потребовать от вас изменить намеченный путь решения задачи

Люди, успешно решающие задачи, как правило, ищут подсказки. Сбор дополнительной информации можно рассматривать как такой поиск. Практически всегда полезно получить максимум возможной информации по интересующей вас задаче. Дополнительные данные помогут реорганизовать пространство задачи и укажут направление, в котором проще искать пути решения.

7. Мозговой штурм. Первоначально он был разработан как метод группового решения задачи, но оказался полезен и для индивидуальной работы. Его целью является выработка как можно большего числа решений. Он призван подтолкнуть людей, занятых решением задачи, к выдвижению самых безумных, невероятных и фантастических идей. Все эти идеи заносятся в список — причем независимо от того, насколько глупыми они кажутся. Принцип, заложенный в основу этой стратегии, заключается в том, что чем больше количество высказанных идей, тем больше вероятность, что по крайней мере одна из них окажется удачной. Чтобы поощрить творческую силу воображения, правила этой стратегии исключают всякую критику и высмеивание идей. Вынесение решения о ценности идей переносится на последующие стадии работы над задачей. Иногда различные идеи частично комбинируются в целях усовершенствования. Мозговой штурм может быть предпринят большой или маленькой группой людей, а также в одиночку. После его проведения перечень возможных решений должен быть тщательно изучен, чтобы найти решения.

5.1 Выбор наилучшей стратегии

Мы рассмотрели несколько различных стратегий, способных оказать помощь при решении задач. Как узнать, какой из них воспользоваться, столкнувшись с конкретной задачей? Важно постоянно помнить, что эти стратегии не являются взаимоисключающими. Часто оказывается полезной их комбинация. Выбор наилучшей стратегии или комбинации стратегий зависит от сути задачи:

1. Если задача является нечетко поставленной, представьте ее цель и условие в нескольких различных формулировках.

2. Если задача имеет несколько (но небольшое количество) возможных решений, имеет смысл воспользоваться методом проб и ошибок.

3. Если задача слишком сложна, попытайтесь применить упрощение, анализ целей и средств, обобщение и специализацию.

4. Если у вас есть возможность собрать дополнительную информацию, сделайте это.

5. Если количество возможных путей решения задачи слишком мало, то, для того чтобы генерировать дополнительные решения, примените мозговой штурм.

6. Использование аналогий—это наиболее широко применяемые стратегии для решения задач любого типа. Надо быть всегда готовым визуализацию и выполнить осмысленный поиск аналогий с целью подбора аналогичного решения.

7. Помните, что это лишь советы по поиску решений задач. Наилучший способ стать высококлассным специалистом по решению задач — это решить как можно больше задач.

Таким образом, решение задачи различными способами требует применения комплекса ранее полученных знаний. А, значит, это процесс систематизации усвоенных учащимися знаний и умений. Решение задач различными способами предоставляет большие возможности для совершенствования обучения математике. При решении задач только одним способом у учащихся единственная цель — найти правильный ответ. Если же требуется применить при этом несколько способов, школьники стараются отыскать наиболее оригинальное, красивое, экономичное решение. Для этого они вспоминают многие теоретические факты, методы и приемы, анализируют их с точки зрения применимости к данной в задаче ситуации, накапливают определенный опыт применения одних и тех же знаний к различным вопросам. При отыскании различных способов решения задач у школьников формируется познавательный интерес, развиваются творческие способности, вырабатываются исследовательские навыки. При этом прежде всего развивается гибкость ума, которая проявляется в быстроте ориентировки в новых условиях, в умении видеть новое в известном, выделять существенное, выступающее в скрытой форме. Нельзя не учитывать и того, что решение задачи различными способами развивает навыки самоконтроля у учащихся, поскольку ответ при всех найденных способах решения одной задачи должен быть одинаков. Решение задачи различными способами – это увлекательный творческий процесс, развивающий воображение, подталкивающий учащегося придумывать, искать все новые и новые решения задачи. Все это активизирует учебную деятельность школьников, прививает интерес к предмету.

Список использованных источников и литературы:

1. , Е.Н. Турецкий. «Как научиться решать задачи» М.,1984.

2. . «Задача одна – решений много». «Математика в школе» №1,1992.

3. «Различные способы решения уравнений и задач по математике для подготовки к ЕГЭ и олимпиадам 7-11 классы.»-Ростонн/Д:Феникс, 2011.

4. , . «Задача одна — решения разные».Киев,1988.

5. Д. Пойя. «Как решать задачу». М.,1959.

6. . «Исследовательская деятельность школьников в процессе решения геометрических задач». «Математика в школе.»№4, 1995

Источник