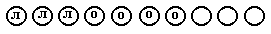Методы решения текстовых задач
 |  | |  |
| арифметический | алгебраический | графический | практический |
| значит найти ответ на требование задачи | |||
| посредством выполнения арифметических действий над числами | составив и решив уравнение или систему уравнений | опираясь только на схематический чертёж или график | выполняя действия с предметами: счётные палочки, спички и т.п. |
ü Арифметический метод.
«Сшили 3 платья, расходуя на каждое по 4 м. ткани. Сколько кофт можно было сшить из этой ткани, если расходовать на одну кофту 2 м.?»
| 1 способ: 1) 4 · 3 = 12 (м) – столько было всего ткани; 2) 12 : 2 = 6 (шт) – столько кофт можно сшить из всей ткани | 2 способ: 1) 4 : 2 = 2 – во столько раз больше ткани израсходовали на платье, чем на кофту; 2) 3 · 2 = 6 (шт) – столько кофт можно сшить |
«Две девочки одновременно побежали навстречу друг другу по спортивной дорожке, длина которой 420 м. Когда они встретились через 30 сек., первая пробежала на 60 м. больше, чем вторая. С какой скоростью бежала каждая девочка?»
Приведены два арифметических способа решений одной и той же задачи, дайте пояснения к каждому действию
| 1 способ: 1) 420 – 60 = 360 (м) 2) 360 : 2 = 180 (м) 3) 180 : 30 = 6 (м/с) 4) 180 + 60 = 420 (м) 5) 240 : 30 = 8 (м/с) | 2 способ: 1) 420 + 60 = 480 (м) 2) 480 : 2 = 180 (м) 3) 240 : 30 = 8 (м/с) 4) 240 – 60 = 180 (м) 5) 180 : 30 = 6 (м/с) |
Ответ: 6 м/с и 8 м/с
ü Алгебраический метод.
«Свитер, шарф и шапку связали из 1 кг. 200 гр. шерсти. На шарф потребовалось на 100 гр. шерсти больше, чем на шапку, и на 400 гр. меньше, чем на свитер. Найти количество шерсти израсходованной на каждую вещь.»
Пусть х (гр) – масса шерсти, израсходованной на шапку, тогда на шарф – (х + 100) гр., а на свитер – ((х + 100) + 400) гр., так как на все три вещи израсходовано 1200 гр., то можно составить уравнение:
х + (х + 100) + ((х + 100) + 400) = 1200
х = 200 (гр) – израсходовали на шапку;
х + 100 = 200 + 100 = 300 (гр) – шарф;
(х + 100) + 400 = 700 (гр) – свитер.
Пусть х (гр) – масса шерсти, израсходованной на шарф, тогда на шапку – (х – 100) гр., а на свитер – (х + 400) гр., так как на все три вещи израсходовано 1200 гр., то можно составить уравнение:
х + (х – 100) + (х + 400) = 1200
х = 300 (гр) – израсходовали на шарф;
х – 100 = 300 – 100 = 200 (гр) – шапка;
х + 400 = 300 + 400 = 700 (гр) – свитер.
Пусть х (гр) – масса шерсти, израсходованной на свитер, тогда на шарф – (х – 400) гр., а на шапку – (х – 400 – 100) гр., так как на все три вещи израсходовано 1200 гр., то можно составить уравнение:
х + (х – 400) + (х – 500) = 1200
х = 700 (гр) – израсходовали на свитер;
х – 400 = 700 – 400 = 300 (гр) – шарф;
х – 500 = 700 – 500 = 200 (гр) – шапка.
Ответ: свитер – 700 гр., шарф – 300 гр., шапка – 200 гр.
ü Графический метод.
«Из двух пунктов навстречу друг другу вышли два пешехода. Первый прошёл 5/8 пути, второй 3/10. Произошла ли встреча?»
5/8
3/10
Ответ: встреча не произошла.
ü Практический метод.
«В совхозе 40 автомашин – легковых и грузовых, причём на каждую легковую машину приходится 4 грузовые машины. Сколько легковых и сколько грузовых машин в совхозе?»
Ответ: 8 легковых машин и 32 грузовые машины.
Вывод: выбор способа решения текстовой задачи не влияет на получение правильного ответа на вопрос задачи.
(лекция 7)
3.3. Этапы решения задач арифметическими способами. Приёмы анализа содержания задачи.
Решение текстовой задачи – процесс сложной умственной деятельности, содержание которой зависит как от конкретной задачи, так и от умений решающего.
Деятельность по решению задачи арифметическим методом включает следующие основные этапы:
Источник
Решение задачи двумя арифметическими способами
СПОСОБЫ РЕШЕНИЯ ЗАДАЧ
Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.
С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.
Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?
Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.
Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.
Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.
Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?
Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим
пойманных рыб: л — лещи, о — окуни.
Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).
1) 3 + 4 = 7 (р.) — пойманные рыбы
Для ответа на вопрос задачи мы выполнили два действия.
Пусть х — пойманные щуки
Тогда количество всех рыб можно записать выражением:
3 + 4 + х — все рыбы
По условию задачи известно, что рыбак поймал всего 10 рыб.
Значит 3 + 4 + х = 10
Решив это уравнение, мы ответим на вопрос задачи.
Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.
В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.
У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?
а) решение по действиям
Ответ: 50 книг на третьей полке.
б) по действиям с пояснением
1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.
2) 90 — 10 = 50 (к.) на 3 полке.
1) Сколько книг на первой и второй полках вместе?
2) Сколько книг на третьей полке?
При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:
90 — (28 + 12) = 50 (к.)
Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.
Например, рассмотренную выше задачу можно решить другим арифметическим способом:
1) 90 — 28 = 62 (к.) на 2 и3 полках.
2) 62 — 12 = 50 (к.) на 3 полке.
В качестве арифметического способа можно рассматривать и такое решение данной задачи:
1) 90 — 12 = 78 (к.) на 2 и 3 полках.
2) 78 -28 = 50 (к.) на З полке.
В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.
Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?
Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:
Ответ: 27 машин было в гараже
В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?
Решение задачи можно оформить так:
48 : 3 = 16 (л.) Ответ: 16 листов
[../../../_private/navbar1.htm]
Источник
Составные задачи, решаемые двумя арифметическими действиями
Ольга Жук
Составные задачи, решаемые двумя арифметическими действиями
Задачи:
совершенствовать вычислительные навыки;
закрепить умение самостоятельно анализировать и решать составные задачи.
развивать зрительное и слуховое восприятие (при выполнении математических заданий);
коррекция и развитие внимания, памяти, мышления (при анализе задач).
воспитывать доброжелательное отношение к окружающим;
воспитывать аккуратность, усидчивость;
учить правильному поведению на уроке: слушать учителя, не перебивать, приступать к выполнению задания, выслушав до конца инструкцию педагога.
таблица умножения, калькулятор;
На уроке используется учебник для 4 класса специальных (коррекционных) образовательных учреждений VIII вида. Авторы– составитель М. Н. Перова
карточки с практическими заданиями;
Ученица Локшина Алина, обучающаяся на дому.
Ход урока:
1. Организационный момент.
— Алина, у нас сегодня урок записывается на камеру. И спустя некоторое время ты сможешь просмотреть наше занятие у себя в ноутбуке.
— Садись за парту, покажи, как правильно надо сидеть за партой.
— Какой урок у нас сегодня? (Урок математики)
Проверим, что у нас должно лежать на столе
Учебник, тетрадь, ручка, карандаш, калькулятор, карточки подсказки, дерево с яблоками
— Чтобы правильно и красиво писать в тетради, надо разогреть твои пальчики.
Пальчиковая гимнастика (формирование произвольности, слухового внимания и восприятия).
Раз, два, три, четыре, (Удар кулачками друг о друга, хлопок в ладоши; повторяют.)
Мы посуду перемыли: (Одна ладонь скользит по другой.)
Чайник, чашку, ковшик, ложку (Загибает пальцы по одному, начиная с большого.)
И большую поварешку.
Мы посуду перемыли: (Одна ладонь скользит по другой.)
Только чашку мы разбили, (Загибает пальчики по одному, начиная с большого.)
Ковшик тоже развалился,
Нос у чайника отбился.
Ложку мы чуть-чуть сломали – (Удары кулачками друг о друга, хлопок в ладоши; повторяет.)
Так мы маме помогали.
Задание на внимание:
Назови посуду, которую мы мыли
Чайник, чашку, ковшик, ложку и большую поварешку
Сегодня какое число?
Вот у этого числа сегодня будет конкурс красоты. Запишем дату
Запишем красиво и аккуратно.
Постановка учебной проблемы и познавательной задачи
-Над какой темой мы работали вчера?
— Чтобы узнать, чем мы сегодня будем заниматься на уроке, помоги мне расставить эти числа в порядке возрастания.
10 18 6 9 20 11
Тема урока: Составные задачи, решаемые двумя арифметическими действиями.
Прочтение на слайде цели урока.
Закрепление имеющихся знаний по теме : «Составные задачи,
решаемые двумя арифметическими действиями».
-Правильно. Сегодня мы продолжим работу над решением задач.
— Какие задачи перед собой поставим?
Закрепить умение решать задачи
Анализировать задачи
Применять полученные знания в жизни.
На уроке ты будешь оценивать себя. Перед нами дерево, если ты выполнишь задание без моей помощи, на дерево прикрепим желтое яблочко, т. е 3б, если с моей помощью, красное яблочко-2 б, если допустишь ошибку, вешаем зеленое яблоко 1 б. На карточке перед тобой записано количество баллов
За яблоко, определенного цвета. В конце урока мы посчитаем набранные баллы и оценим урок.
Желтое яблоко-3 б
Красное яблоко-2 б
Зеленое яблоко-1 б
Для оценки» 5» нужно набрать 12-15 б.
Для оценки «4 «нужно набрать 8-11 б.
Для оценки «3 «нужно набрать 5- 7 б.
Так же я буду тебе добавлять баллы за аккуратность, быстрое и правильное выполнение задания. Перед тобой еще большое яблоко, на нем в конце урока ты нарисуешь на нем смайлик, соответствующий твоему настроению
Проверка домашнего задания
А) Счет десятками
Повторение компонентов арифметических действий.
Учитель дает ученику карточки,с помощью которых он ответит на вопросы:
первое слагаемое второе слагаемое сумма
уменьшаемое вычитаемое разность
первый множитель второй множитель произведение
делимое делитель частное
— Как называются числа при сложении (вычитании, умножении, делении?
Ученик выбирает необходимую карточку-ответ.
-Как изменяются числа при сложении? (Увеличиваются на несколько единиц).
— Как изменяются числа при вычитании? (Уменьшаются на несколько единиц).
— Как изменяются числа при умножении? (Увеличиваются в несколько раз).
— Как изменяются числа при делении? (Уменьшаются в несколько раз).
3. Арифметический диктант.
Первое слагаемое – 20, второе слагаемое 27. Найди сумму. (47)
Уменьшаемое 77, вычитаемое 70. Найти разность. (7)
Первый множитель 9, второй множитель 6. Найди произведение. (54)
8 уменьшить в 4 раза. (2)
Ф. м музыкальная
Закрепление имеющихся знаний по теме : «Составные задачи,
решаемые двумя арифметическими действиями».
Задача № 1 : В соревнованиях участвовало 33 девочки, а мальчиков– на 10 меньше. Сколько всего детей участвовало в соревнованиях?
Учитель задает вопросы по условию задачи:
— Кто участвовал в соревнованиях? (Мальчики и девочки)
Что нам известно?
— Что нам известно про мальчиков из условия задачи?
— Каков вопрос задачи?
— Сколько было девочек? (33 дев.)
— Сколько было мальчиков? Известно? (Нет)
— Что значит на 10 меньше? Какой выберем знак? (Знак минус)
— Что найдем в первом действии? (Сколько мальчиков)
— Что найдем во втором действии? (Сколько всего детей)
— Сколько вопросов в задаче? (Два)
— Во сколько действий будем решать задачу? (В два)
Ученик читает условие задачи, отвечает на вопросы учителя
В ходе работы над задачейученик моделирует схему:
Мальчики-? На 10 меньше
Что нужно узнать?
Сколько всего детей
Можем ответить на вопрос задачи?
Ученик с помощью учителя записывает краткое условие задачи и решение.
Задача № 2 : В школьной столовой было39 ножей, вилок – на 12 больше, а ложек – столько, сколько вилок и ножей вместе. Сколько ложек получила столовая?
Учитель задает вопросы по условию задачи:
— Сколько было ножей в столовой? (39 ножей)
— А сколько вилок? Нам известно? (Нет)
— Что значит: «на 12 больше?». Какой выберем знак (плюс или минус?
— Что найдем вначале
— Что найдем потом?
— Сколько вопросов в задаче? (Два)
— Во сколько действий будем решать задачу? (В два)
Учитель читает условие задачи, ученица отвечает на вопросы учителя Ученица с помощью учителя записывает краткое условие задачи и решение.
Итог урока. Учитель подводит итог.
— Алина, что мы сегодня делали на уроке?
Ученица отвечает: решали примеры, повторяли таблицу умножения, решали задачи.
Что нужно сделать, чтоб решить задачу в 2 действия?
Ученица показывает свою работу в тетради.
Рефлексия. Перед тобой яблоко, нарисуй на нем смайлик, соответствующий твоему настроению
8. Домашнее задание. стр. 118 №19 (1,2 ст.).
Учитель: сейчас открывай дневник и записывай домашнее
задание.
9. Оценка деятельности учащейся.
Посмотри, какое красивое дерево у нас получилось
Учитель: ты сегодня хорошо работала на уроке! Давай посчитаем, сколько яблок и какого цвета у нас на дереве. Посчитаем баллы.
(Оценивание работы учащейся на уроке).
Цели и задачи АОП дошкольного образования ДОО компенсирующего вида Адаптированная образовательная программа дошкольного образования в условиях ДОУ компенсирующего вида направлена на реализацию следующих.
Дидактическая игра по развитию художественного творчества «Цветные задачи» Предлагаю вашему вниманию игру для детей от четырёх лет по развитию художественного творчества. Используем игру при знакомстве детей с основными.
Консультация для педагогов «Игровые занимательные задачи для дошкольников» Для успешного освоения программы дошкольного обучения ребенку необходимо не только много знать, но и последовательно мыслить, догадываться,.
Математические задачи для детей в стихотворной форме 1. Как-то стал считать я звёзды,насчитал всего лишь семь, вдруг одна звезда исчезла и пропала насовсем, сколько в небе светит звёзд,у кого.
Опрос детей «Рисование» в рамках реализации годовой задачи В одной известной песни поется: «Это правда! Ну чего же тут скрывать? Дети любят, очень любят рисовать!» Одна из годовых задач нашего.
Задачи для учащихся 6–11 классов «Проценты в профессиях» Проценты в профессиях (6-11 классы)Проценты широко применяются в нашей жизни. Посмотрим, в каких профессиях они встречаются чаще всего.
Проектные задачи в начальной школе Проектная задача — система заданий, целенаправленно стимулирующая действия детей на получение ещё никогда не существовавшего в практике.
Самоанализ педагогической деятельности: цели, задачи и методика работы Я, Прилепко Евгения Александровна, работаю в МКДОУ № 196 воспитателем, педагогический стаж работы 26 лет. Приоритетным направлением в детском.
Видеоотчет «Решение логической задачи на занятии по ФЭМП» Уважаемые коллеги! Предлагаю вашему вниманию видеофрагмент занятия по математике в старшей группе. Логическая задача по сказке Киплинга.
Экспериментальная деятельность в детском саду: задачи, методы и приемы Экспериментальная деятельность в детском саду Ребёнок-дошкольник активно стремится узнать об окружающем его мире как можно больше. Наряду.
Источник
