Решение задачи аналитическим способом примеры

Аналитический метод решения

При аналитическом методе решения отправляются не от условия задачи, как это делают при синтетическом методе, а от ее требования, вопроса. Это характерно для всех разновидностей аналитического метода, применяемых при решении задач.

Решение задач аналитическим методом начинается с постановки следующего вопроса, связанного с требованием решаемой задачи: «Что нужно знать, чтобы ответить на вопрос данной задачи (выполнить требование)?» Для правильного ответа на поставленный вопрос необходимо знать данные задачи и учитывать те зависимости, которые связывают их с искомым числом.

Пусть для вычисления искомого Y основной задачи требуется знать, например, числа p₁ и q₁, из которых при помощи некоторого математического действия можно получить Y, т.е. решить основную задачу. Итак, основная задача с требованием Y преобразовалась в первую серию вспомогательных задач с искомыми p₁ и q₁. Обозначим первую серию вспомогательных задач через В₁. Ставим тот же вопрос к каждой из вспомогательных задач: «Что нужно знать, чтобы найти p₁ (q₁)?» и опять при ответе на этот вопрос используем условие А основной задачи, а также арсенал математической теории.

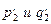
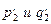
Пусть для вычисления p₁ нужно знать p₂ и q₂, а для вычисления q₁ – знать . Теперь основная задача преобразовалась во вторую серию (В₂) вспомогательных задач, включающих задачи по нахождению p₂, q₂, .

Продолжая процесс преобразования, получаем, наконец, такую серию (В_n) вспомогательных задач, искомые которых содержатся во множестве данных основной задачи.

Итак основная задача решена аналитическим методом, поскольку этим методом проведен поиск и найден путь решения задачи; главное здесь именно в этом, а не в оформлении записи уже известного решения.

Найденное аналитическое решение можно изложить различными способами, в том числе и синтетическим. В последнем случае пришлось бы следовать от конца аналитического рассуждения к его началу, не производя при этом никаких поисков.

Если основную задачу условно записать формулой А У, описанный выше аналитический путь преобразования задачи изобразится схемой:

,

Где А В_n, В_n B_n-1, . . . , В₁ У, откуда А У.

К рассмотренной в предыдущем пункте текстовой задаче применим аналитический метод решения. Наличие двух искомых в задаче несколько осложняет построение рассуждений, поэтому можно ограничиться сначала одним искомым, найти его и затем воспользоваться им как уже известным числом при отыскании пути получения второго искомого. Рассмотрим схему:

• За сколько часов может выполнить всю работу, работая отдельно, та машина, которая продолжила работу?
• Часть всей работы, выполненная этой машиной.
• Сколько часов работала эта машина отдельно когда она работала отдельно
• Объем всей работы
• Часть всей работы, выполненная двумя машинами совместно
• За сколько часов машины вместе Выполнят всю работу?
• Сколько часов они работали совместно?

Такой поиск обычно проводится устно и завершается составлением плана решения. Аналогично теперь можно построить схему аналитического поиска второго числа основной задачи (сделайте самостоятельно!).

В практике решения задач методы анализа и синтеза полностью разделить, изолировать друг от друга невозможно. Они полезно сочетаются. При аналитическом методе имеют место скрытые элементы синтеза. Например, преобразуя требование основной задачи в требования первой серии вспомогательных задач, мы неявно проверяем правильность этого преобразования, возможность синтезирования из искомых чисел задач первой серии искомого основной задачи.

Широкое применение находит аналитический метод при решении геометрических задач на вычисление. Здесь удобно начинать решение с соответствующей формулы, которая и показывает, какой будет первая серия вспомогательных задач и т.д. Кратко продемонстрируем это на примере следующей геометрической задачи.

Задача. В конус вписана пирамида, основанием которой служит прямоугольный треугольник и боковая грань которой, проходящая через один из катетов основания, образует с плоскостью основания двугранный угол α. Найти объем пирамиды, если образующая конуса равна l и наклонена к плоскости основания под углом β.

Р е ш е н и е. Начертим конус с вписанной в него пирамидой МАВС, в которой длины боковых ребер МА = МВ = МС = l, АС – гипотенуза треугольника АВС, центр основания конуса – точка О, Ао = ОС, ÐМАО=β, ÐМDО = α.

Формула объема пирамиды 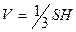. Задача сводится к нахождению площади основания S и высоты H = MO. (Первая серия из двух вспомогательных задач; последнюю из этих задач можно решить по имеющимся данным.).

Из прямоугольного треугольника ОМА находим Н = ОМ = lsinβ.

Для нахождения площади основания надо найти длины катетов АВ и ВС. (Получаем вторую серию из двух вспомогательных задач.)

Для определения АВ достаточно найти ОD – длину средней линии треугольника АВС, а для вычисления ВС надо найти АС ( третья серия из двух вспомогательных задач; решение первой задачи уже известно):

OD = MO ctgα = l sinβ ctg α.

Для получения АС достаточно знать АО ( четвертая серия – одна задача, которую можно решить):

; ; ;

;

;

.

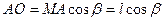
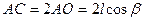
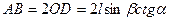
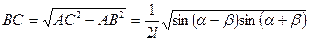
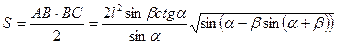
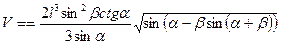
Приведенное решение является очень кратким (отсутствуют выкладки, обоснования), чтобы выделить метод решения. Учащиеся, чтобы научиться решать задачи, должны делать полные математические выкладки и уметь обосновывать каждый свой шаг в процессе решения ссылкой на условие задачи или изученную математическую теорию.

Хотя путь поиска на основе аналитического метода решения не всегда однозначен, однако он все же менее многозначен и более определен, чем путь поиска при синтетическом методе решения. Аналитический метод удобен для поиска пути решения новой для учащихся задачи, он опирается на определенное умение школьника рассуждать и эффективно способствует развитию его продуктивного, логического и функционального мышления. В результате систематического применения аналитического метода решения задач у учащихся быстрее формируется умение cамостоятельно решать новые для них задачи, чем при пользовании синтетическим методом.

Источник

Методическое пособие «Решение геометрических задач аналитическим способом»

по теме: «Решение геометрических задач аналитическим способом»

АНАЛИТИЧЕСКИЙ МЕТОД РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ

Уравнения первой и второй степени

Алгебраические преобразования. Тождества и неравенства

Тригонометрические тождества и уравнения

Уравнения и неравенства смешанного вида

Задачи на построение

Задачи на отыскание наибольших и наименьших значений

Зависимости между элементами треугольника

Зависимости между элементами четырехугольника

Зависимости между элементами тетраэдра

Решение задач по математике имеет большое общеобразовательное и воспитательное значение. Процесс решения задачи представляет собой поиск выхода из затруднения или пути обхода препятствия, — это процесс достижения цели, которая первоначально не кажется сразу доступной [7]. Решение задач является специфической особенностью интеллекта, а интеллект – это особый дар человека; поэтому решение задач может рассматриваться как одно из самых характерных проявлений человеческой деятельности [11]. Поиск решения нестандартной задачи развивает инициативу, настойчивость и сообразительность.

Сборник: «Решение геометрических задач аналитическим способом» рассчитан на то, чтобы показать рациональность применения аналитического способа при решении геометрических задач во время подготовки к выпускным экзаменам, тестированию.

1 АНАЛИТИЧЕСКИЙ СПОСОБ РЕШЕНИЯ ГЕОМЕТРИЧЕСКИХ ЗАДАЧ.

Уравнения первой и второй степеней.

В начале приведем примеры задач по геометрии, приводимые к алгебраическим уравнениям первой и второй степени.

Для решения таких задач следует сделать чертеж и составить уравнение, выражающие связь между данными и неизвестными элементами фигуры [6].

Пример 1. Длины боковых сторон трапеции равны 3 и 5. известно, что в трапецию можно вписать окружность. Средняя линия трапеции делит ее на две части, отношение площадей которых равно 5/11.

Найти длины оснований трапеции [9].

Обозначим ВС=х, AD =у, т.к. в четырехугольник ABCD можно вписать окружность, то х+у= BC + AD = AB + CD =8. Поскольку KL — средняя линия трапеции, то из теоремы о пропорциональных отрезках отсекаемых параллельными прямыми, следует, что высоты трапеций KBCL и AKLD равны h /2. Для площадей этих трапеций имеем

Алгебраические преобразования. Тождества и неравенства.

Часто в повседневной жизни мы можем услышать, что кто-то купил новую вещь, совершил какую-либо глупость, употребил грубое выражение и многое другое. Но это всего лишь слухи, а так ли это на самом деле задумывается не каждый. Тот, кто воспринимает этот слух всерьез, имеет перед собой готовую «задачу на доказательство»: ему предстоит снять со слуха покров сомнения, он должен доказать (или опровергнуть), что данное действие было совершено, и это доказательство или опровержение должно быть им мотивировано со всей доступной в данном случае убедительностью. Когда мы встречаемся с математической задачей на доказательство, нам предстоит снять сомнение в правильности четко сформулированного математического утверждения — мы должны доказать или опровергнуть его.

При решении задач на доказательство находят применение тождества и неравенства, известные из школьного курса алгебры. Некоторые задачи могут быть решены способом составления уравнений [3] .

Пример 2. Дан треугольник ABC , в котором АВВС. Доказать, что биссектриса угла В лежит между медианой и высотой, проведенными из той же вершины В [4].

Пусть BC = a , AC = b и AB =с (с≠а)

Если угол С – тупой, то основание высоты BD лежит на продолжении стороны AC и значит AD > b > AF . В этом случае AD > AF > AM , т.е. биссектриса BF лежит между медианой BM и высотой BD .

Пусть С – острый угол, найдем AD . Пусть AD= x . Из ∆ ABD ; имеем: BD 2 = AB 2 — AD 2 , BD 2 = BC 2 — DC 2 , откуда c 2 -x 2 =a 2 -(b-x) 2 . . Покажем, что:

D> AF , т.е. . Рассмотрим разность: .

Т.к. c > a и с+ a > b , то разность положительна. Отсюда AD > AF . Итак, AD > AF > AM , биссектриса BF лежит между медианой BM и высотой BD .

Тригонометрические тождества и уравнения.

Тригонометрические функции находят применение при решении самых разнообразных задач. Существуют задачи, приводимые к тригонометрическим уравнениям, а так же задачи, решаемые путем введения вспомогательных неизвестных. При решении задачи аналитическим методом не требуется остроумных вспомогательных построений, задача сводиться к применению формул, решено уравнение, доказательству тождеств.

Пример 3. В равнобочной трапеции основание AD равно диагонали AC . Известно, что CAD = CDM , где М – середина ВС. Найти углы трапеции [5].

Дано: ABCD – равнобедренная трапеция; AD = AC ; M – середина ВС; CAD = CDA

Найти: BAD , ABC

Пусть CAD = φ , тогда ADC = ACD =90 0 — φ /2. Поскольку по условию MDC = CAD = φ , то CMD = MDA = ADC — MDC =90 0 -3/2 φ , MCD =90 0 + φ /2. По теореме синусов для треугольника MCD найдем:

Но М – середина ВС следовательно, проекция MD на , т.е. .

Из равнобедренного треугольника ACD найдем .

Приравняем:

Таким образом:;

Ответ: ,

Уравнения и неравенства смешанного вида.

Геометрические задачи на вычисление углов иногда приводят к уравнениям более сложного вида, чем тригонометрические уравнения. Например, одна из частей уравнения может быть линейной функцией неизвестного угла, а другая – тригонометрической функцией того же угла. Уравнения такого вида могут быть решены приближенно графическим методом и методом проб. Иногда целесообразно пользоваться обоими способами [2] .

Пример 4. В прямоугольном треугольнике ABC катет AB равен 3, катет АС равен 6. Центры окружностей радиусов 1,2 и 3 находятся соответственно в точках А, В, С. Найти радиус окружности, касающийся каждой из трех данных окружностей внешним образом [4].

Дано:,

Сделаем скелетный чертеж. Нам достаточно провести отрезки OA , OB , OC , где О – центр искомой окружности. Если радиус четвертой окружности равен х, то АО=1+х, ОВ=2+х, ОС=3+х. Введем еще одно неизвестное: , тогда .

Запишем теорему косинусов для треугольников АОС и АОВ. Получим систему уравнений:

Выразим из первого уравнения , а из второго

Используем соотношения

Ответ:

Задачи на построение.

Алгебра и тригонометрия находят применение не только при решении задач на вычисление и на доказательство, но и при решении задач на построение. Задачи на построение являются традиционными задачами в курсе геометрии. Разработкой методов решения этих задач математики занимаются еще со времени Древней Греции [1].

Задачей является непосредственное применение алгебраического метода к геометрическим построениям. Простейшие примеры такого применения изучают еще в школьном курсе геометрии. Так, каждый из нас знает, что построение четвертого пропорционального к трем данным отрезкам выражается формулой . Со школы, знаем построение, дающее отрезок , т.е. среднее пропорциональное двух данных отрезов. Умеем строить гипотенузу с прямоугольного треугольника по данным его катетам, т.е. выполнять «построение» для формулы . Умеем построить катет прямоугольного треугольника по данным гипотенузе и другому катету, что соответствует формуле и т.п. Все эти простейшие построения должны быть хорошо известны, т.к. в конечном счете, именно к ним сводится всякое более сложное применение алгебраического метода [12].

Пример 5. В данную окружность вписать прямоугольник, равновеликий данному квадрату [12].

АНАЛИЗ: пусть в окружность вписан прямоугольник ABCD , равновеликий квадрату со стороной а. Диагональ АС прямоугольника можно построить: она является диаметром окружности; треугольники АВС и ACD конгруэнтны, задача будет решена, если удастся построить точку В, а для этого достаточно построить высоту BH треугольника АВС.

Пусть АС=α и ВН= х. Выразим площадь прямоугольника ABCD через α и х, приравняв её площади данного квадрата, получим уравнение αх=а 2 , откуда х=а 2 /α.

ИССЛЕДОВАНИЕ. Задача имеет решение тогда и только тогда, когда х=а 2 /α, а это равносильно условию (диаметр окружности не меньше диагонали данного квадрата).

ПОСТРОЕНИЕ. В начале построим отрезок ВН, пользуясь полученной формулой . Для этого проведем диаметр АС данной окружности и на окружности построим точку М, так, чтобы АМ=а. Тогда получим: перпендикуляр МЕ к диаметру АС. Тогда получим: . После чего остается на расстоянии х которая пересечет окружность в точке В, и построить точку D симметричную В относительно центра окружности.

ДОКАЗАТЕЛЬСТВО. Т.к. АС и BD – диаметры окружности, то ABCD – прямоугольник. Площадь S прямоугольника равна площади квадрата со стороной а, действительно, .

Легко убедиться в том, что если за неизвестное х принять длину стороны прямоугольника, то формула, выражающая х через длины данных отрезков, окажется громоздкой, и для решения задачи придется выполнить более сложные построения. Таким образом, выбор неизвестных при решении задачи алгебраическим методом имеет существенное значение.

Задачи на отыскание наибольших и наименьших значений.

Задачи на максимум и минимум могут быть также решены элементарными средствами, без использования производной. Одни из них сводятся к нахождению наибольшего или наименьшего значения квадратного трехчлена, другие – к исследованию выражении, содержащего тригонометрические функции.

Хорошо известно, что решение «экстремальных» задач, независимо от того, ч то относятся ли они к арифметике, алгебре, геометрии или математическому анализу, могут строиться двумя принципиально различными путями. Прямым называется такое доказательство какого-либо экстремального свойства, в котором, скажем, определяется фигура непосредственно сравнивается с производной другой фигурой, удовлетворяющей всем условиям поставленной задачи, и оказывается, что первая фигура лучше (или не хуже) каждой другой. Напротив, косвенное доказательство сводиться к рассуждению, показывающему, что все фигуры, кроме какой-то одной (или нескольких), не могут служить решением задачи, поскольку для каждой такой фигуры можно найти другую лучшую, чем она, откуда уже и делается вывод о том, что решение задачи является та единственная фигура, которую мы не можем «улучшить» [3].

Пример 6. Периметр треугольника ABC равен 2р. Какое наибольшее значение может иметь длина заключенного внутри треугольника и параллельного ВС отрезка касательной к вписанной в АВС окружности? Для какого треугольника (каких треугольников) достигается это значение [13]?

Пусть вписанная окружность S треугольника касается его сторон ВС ,АС и АВ длин а, в и с в точках D , Е и F , а прямой KL (где ) — в точке М. Из равенства длин касательных, проведенных из одной точки, следует, что и

Таким образом, периметр 2Р треугольника ALK равен:

Из ∆ABC

, где

Таким образом, наибольшее возможное значение длины m отрезка KL достигается для всех треугольников ABC с основанием

(т.е. в+с=3а); это значение равно

Ответ: для треугольников с основанием .

Зависимости между элементами треугольника.

Среди задач по геометрии встречаются задачи, касающиеся треугольников. Здесь используются теоремы синусов и косинусов, а также формулы, выражающие элементы треугольника через его стороны [5].

Пример 7. В равнобедренном треугольнике KLM длина основания КМ равна а, а длина высоты, опущенной из точки К на боковую сторону ML , равна h . Найти длины всех медиан треугольника [6].

Дано ∆ KLM , KL = LM , KM =а, KP = h , LR = RM , KQ = QM

Рассмотрим ∆ KPM ,

. N — точка пересечений медиан
Откуда

Ответ:

Зависимости между элементами четырехугольника.

Решения их можно получить средствами алгебры и тригонометрии. В некоторых случаях полезно прибегать к вспомогательным построениям, именно с помощью них порой можно очень быстро увидеть правильный путь к получению результата.

Пример 8. В окружность вписан четырехугольник ABCD , диагонали которого взаимно перпендикулярны и пересекаются в точке Е. Прямая, проходит через точку Е и перпендикулярная к АВ, пересекает сторону CD в точке М. доказать, что ЕМ – медиана треугольника CED , и найти ее длину, если AD =8см, АВ=4см и CDB = [2].

Дано: AD =8см; АВ=4см; CDB =

Обозначим через К точку пересечения прямых АВ и ЕМ. Поскольку углы CDB и CA B опираются на одну дугу, то . Из равенства, что это означает, что — равнобедренный, т.е.

Итак, — равнобедренный DM = EM . Доказано, что СМ= DM или, что ЕМ – медиана. Из . Из

Ответ:

Зависимости между элементами тетраэдра.

Рассмотрим метрические соотношения между элементами тетраэдра (произвольной треугольной пирамиды – простейшего из всех многогранников, играющего в стереометрии ту же роль, какую в планиметрии играет треугольник). Что же касается свойств тетраэдра, иногда они в точности аналогичны свойствам плоского треугольника, а иногда своеобразно преломляют известные из планиметрии факты [8].

Пример 9. Ребра равногранного тетраэдра равны а, в и с. Вычислите его объем V и радиус R описанной сферы [10].

Решение: Достроим данный тетраэдр до прямоугольного параллелепипеда; пусть x, y и z – ребра этого параллелепипеда. Тогда и

Так как , где — диагональ параллелепипеда, а , то

Следовательно равенства и и вычитая из них равенство , получаем

Аналогично находим и . Так как объем тетраэдра в три раза меньше объема параллелепипеда, то

Ответ: ;

Таким образом, применение дополнительного построения позволяет упростить решение задачи.

Александров А.Д., Вернер А.А., Рыжик В.И. Геометрия. – М.: просвещение, 1995

Владимиров Ю.Н., Королько Е.А., Фролова И.В. Математика. Учебное пособие для абитуриентов, — 2-е изд., исправ. – Новосибирск: НГУЭУ, 2006. – 192 с.

Готман Э.Г., Сконец З.А. Решение геометрических задач аналитическим методом. – М.: Просвещение, 1979

Дополнение к сборнику заданий для проведения письменного экзамена по математике за курс 11-летней школы с углубленным изучением математики (геометрии).

Жарыгин И.Ф. Факультативный курс по математике / учеб. Пособие для 10 класса средней школы /. – М.: 1989

Методическое пособие по математике для поступающих в Московский институт стали и сплавов. – М.: 1970

Пойа Д. Математическое открытие. – М.: Наука, 1976

Прасолов В.В., Шарыгин И.Ф. Задачи по стереометрии. – М.: Наука, 1989

Сборник тестов по математике./Учебно-методическое пособие. Астана: РГКП «Национальный центр государственных стандартов образования и тестирования», 2012. – 251 с.

Сборник тестов по математике./Учебно-методическое пособие. Астана: РГКП «Национальный центр государственных стандартов образования и тестирования», 2012. – 224 с.

Фридман Л.М., Турецкий Е.Н. Как научится решать задачи. – М.: просвещение, 1984

Четверухин Н.Ф. Методы геометрических построений: Учпедку -1952

Шклярский Д.О., Ченцов Н.Н., Яглом И.М. Геометрические неравенства и задачи на максимум и минимум. М: Наука, 1970

Источник