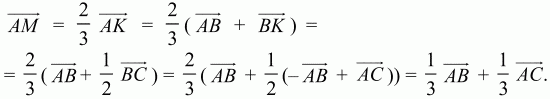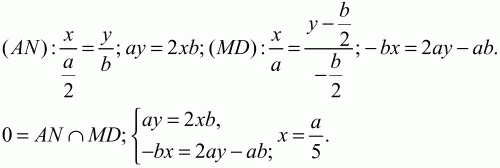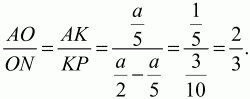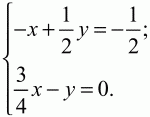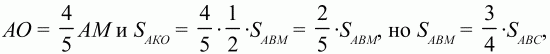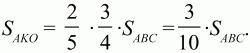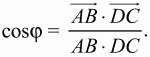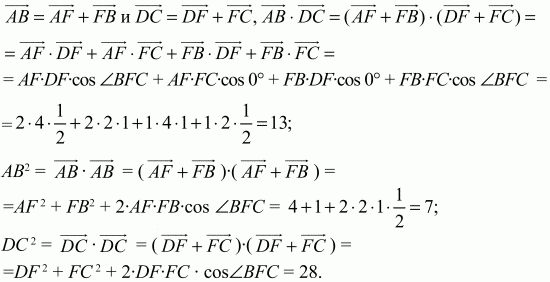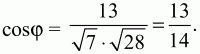Решение задач векторным способом 9 класс

Вообще говоря, в данном случае речь идет не о частных идеях решения определенного класса задач, а об универсальных методах решения самых разнообразных геометрических проблем.

Суть метода состоит в том, что для решения задач вводится система координат (прямоугольная или аффинная), пишутся необходимые уравнения прямых, других фигур, по известным формулам находятся длины и углы.

Примеры решения задач

149. Даны точки А(-2; 1); В(1; 5); С(3; -2); D(6; 2). Является ли четырёхугольник ABCD параллелограммом? Ответ: обоснуйте.

Решение. АВ = (3; 4); CD = (3; 4). Противоположные стороны четырёхугольника, таким образом, равны и параллельны. Значит, ABCD – параллелограмм.

Ответ: ABCD – параллелограмм.

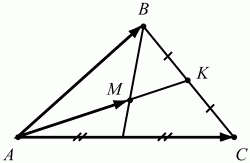
150. В треугольнике ABC точка М – точка пересечения медиан. Выразите вектор AM через вектора АВ и АС (рис. 205).

Решение. Медианы точкой пересечения делятся в отношении 2:1, считая от вершины, поэтому

Задачу можно решить проще, если достроить треугольник ABC до параллелограмма ABDC, тогда AM = 2/3 АК, но АК = 1/2 AD = 1/2 (АВ + АС). Отсюда сразу получаем, что AM = 1/3(АВ + АС).

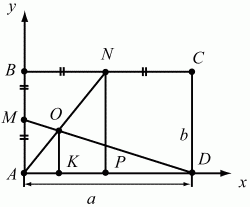
151. В прямоугольнике ABCD точки М и N – середины сторон АВ и ВС. Точка О – точка пересечения AN и DM. Найдите AO/ON (рис. 206). (2)

Решение. Решим задачу аналитическим путём. Пусть А(0; 0); D (a; 0); B(0; b), тогда M(0; b/2); N(a/2; b). Напишем уравнения прямых AN и MD.

Точка О будет иметь координаты:

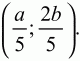
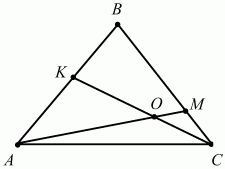
152. ВМ: МС = 3:1, АК = КВ. Найдите: SAKO/SABC (рис. 207). (3)

Решение. См. задачу 105 (с. 88). Тогда мы решили её, применив теорему о пропорциональных отрезках. Здесь мы применим векторный подход и метод неопределенных коэффициентов.

Пусть ВА = а, ВС = b, АО = х ? AM, КО = у ? КС, тогда АО + ОК = АК, х ? АМ + (-у ? КС) = -1/2а.

Так как AM = AB + ВМ = – ВА + 3/4ВС = – а + 3/4b и КС = KB + ВС = -1/2ВА + ВС = -1/2а + b, то с учётом этого получаем уравнение: хAM + (-уКС) = -1/2а или х(-а + 3/4b) – у(-1/2а + b) = -1/2а. Приравнивая к нулю коэффициенты при векторах а и b, стоящих в левой и правой частях уравнения, получим систему:

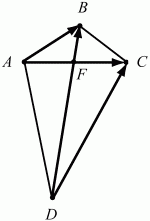
153. В выпуклом четырёхугольнике ABCD диагонали АС и BD пересекаются в точке F. Известно, что AF = CF = 2, BF = 1, DF = 4, ?BFC = ?/3.

Найти косинус угла между векторами АВ и DC (рис. 208).

Пусть ? – искомый угол между векторами АВ и DC тогда

Пользуясь свойствами скалярного произведения векторов и условиями задачи, вычислим АВ, DC и АВ ? DC. Так как

Теперь получаем, что

Задачи для самостоятельного решения

154. Найдите геометрическое место точек, равноудалённых от данной прямой и данной точки.

155. Продолжения сторон AD и ВС четырёхугольника ABCD пересекаются в точке Р. Точки М и N – середины сторон АВ и CD. Доказать, что если прямая MN проходит через точку Р, то ABCD – трапеция.

156. Дан равнобедренный треугольник ABC, в котором проведены высота CD и перпендикуляр DE к боковой стороне ВС. Точка M – середина отрезка DE. Доказать, что отрезки АЕ и СМ перпендикулярны.

157. Доказать, что для треугольника ABC и любой точки Р выполняется неравенство:

Источник

Презентация для 9 класса по теме «Решение задач по теме «Векторы»

Описание презентации по отдельным слайдам:

Решение задач по теме «Векторы» (9 класс)

Цели урока: ۩Систематизировать ЗУН учащихся по изучаемой теме; ۩Совершенствовать навыки решения задач на применение теории векторов; ۩Подготовить учащихся к контрольной работе.

Решение задач по готовым чертежам: 1. 2.

Самостоятельное решение задач:

Домашнее задание: дорешать номера для самостоятельной работы, подготовиться к контрольной работе.

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 821 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 290 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 605 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДВ-156311

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

В Тюменской области продлили на неделю дистанционный режим для школьников

Время чтения: 1 минута

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Руководители управлений образования ДФО пройдут переобучение в Москве

Время чтения: 1 минута

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Векторный метод и его применение к решению задач школьного курса геометрии
методическая разработка по геометрии (9 класс) по теме

Выпускная квалификационная работа по специальности «Математика»

Скачать:

Вложение	Размер
diplomnaya_rabota.docx	587.55 КБ
prilozhenie.docx	363.55 КБ

Предварительный просмотр:

Глава 1 Векторная алгебра 5

1.1. Понятие вектора; сложение и вычитание векторов

1.1.1. Понятие вектора 5

1.1.2. Нуль-вектор 6

1.1.3. Коллинеарные векторы 6

1.1.4. Модуль вектора 7

1.1.5. Равенство векторов 7

1.1.6. Перенос вектора в данную точку 8

1.1.7. Сумма двух векторов 8

1.1.8. Основные свойства сложения векторов 9

1.1.9. Сложение нескольких векторов 10

1.1.10. Вычитание векторов 11

1.1.11. Модули сумм и разностей векторов 12

1.2. Умножение вектора на число

1.2.1. Умножение вектора на число 13

1.2.2. Основные свойства произведения вектора на число 13

1.3. Линейная зависимость

1.3.1. Линейная комбинация векторов 16

1.3.2. Линейная зависимость векторов 16

1.3.3. Система коллинеарных векторов 17

1.3.4. Система компланарных векторов 18

1.3.5. Базис системы компланарных векторов 18

Глава 2 Методические рекомендации 21

2.1. Векторы в школьном курсе геометрии 21

2.2. Методика решения задач аффинной геометрии векторным методом 24

2.2.1. Цели изучения векторного метода в средней школе 24

2.2.2. Основные компоненты векторного метода решения задач 25

2.2.3. Понятийный аппарат 25

2.2.4. Типовые задачи аффинной геометрии, решаемые векторным методом 26

2.3. Решение типовых задач элементарной геометрии векторным методом 30

2.3.1. Задачи, связанные с доказательством параллельности прямых и отрезков, прямых и плоскости. 30

2.3.2. Задачи на доказательство деления некоторого отрезка в заданном отношении или на нахождение отношения, в котором делится отрезок 33

п 2.3.3. Задачи на доказательство или использование принадлежности трёх точек прямой 38

Актуальность темы исследования: традиционно одной из самых сложных тем школьного курса геометрии является тема “Применение векторов к решению задач”. В то же время понятие вектора является одним из фундаментальных понятий современной математики, а векторный метод является одним из широко употребляемых, красивых и современных методов решения задач.

Гипотеза: успешность овладения учащимися векторным методом решения геометрических задач зависит от умения переходить от геометрического языка к векторному и обратно.

Основные цели данного исследования:

1.рассмотреть цели изучения векторного метода в школе;

2.выделить основные компоненты решения задач этим методом;

3.рассмотреть понятийный аппарат векторного метода решения задач;

4.классифицировать задачи аффинной геометрии, решаемые векторным методом

Для достижения поставленной цели решались следующие задачи: изучить психолого-педагогическую и научно-методическую литературу по данной проблеме, выявить наиболее эффективную методику формирования векторного метода решения задач аффинной геометрии в школе.

Объектом исследования выступает векторный метод решения задач аффинной геометрии.

Предмет исследования — методика формирования векторного метода решения задач аффинной геометрии в школе.

В процессе работы над исследованием были использованы следующие методы и приёмы:

анализ научной и методической литературы
изучение и обобщение опыта передовых учителей
анализ школьных учебников

Новизна исследования заключается в том, что в результате работы по данной проблеме был отобран и систематизирован методический материал, соотнесены геометрические и векторные интерпретации аффинных задач, разработаны опорные таблицы по теме «Векторы», а также разработаны конспекты уроков 9 классе по данной теме.

Практическая значимость: знание векторных интерпретаций задач аффинной геометрии способствует эффективному формированию навыка решения задач векторным методом.

Структура ВКР: работа состоит из введения, двух глав, заключения, библиографического списка, приложения.

В первой главе рассмотрен теоретический материал о линейных операциях над векторами, а также коллинеарных и компланарных векторах.

Во второй главе рассмотрены место и цели изучения темы «Векторы» в школьном курсе геометрии, методика решения задач аффинной геометрии векторным методом, приведена классификация задач аффинной геометрии, решаемых векторным методом и решены некоторые задачи каждого типа

В заключении делаются выводы и обобщения.

ГЛАВА 1.ВЕКТОРНАЯ АЛГЕБРА

1.1. ПОНЯТИЕ ВЕКТОРА, СЛОЖЕНИЕ И ВЫЧИТАНИЕ ВЕКТОРОВ.

1.1.1. ПОНЯТИЕ ВЕКТОРА

Многие геометрические и физические величины полностью определяются, если задана их числовая характеристика. Такими величинами являются длина линии, объем тела, масса, работа, температура и т. д. Число, характеризующее ту или иную величину, получается в результате сравнения ее с выбранным эталоном, принятым за единицу измерения. Такие величины в математике называются скалярными величинами или просто скалярами.

Однако иногда встречаются величины более сложной природы, которые не могут быть полностью охарактеризованы их числовым значением. К подобным величинам относятся сила, скорость, ускорение и т. д. Для полной характеристики указанных величин, кроме числового значения, необходимо указать их направление. Такие величины в математике называются векторными величинами или векторами.

Для графического изображения векторов пользуются направленными отрезками прямой. В элементарной геометрии, как известно, отрезком называется совокупность двух различных точек А и В вместе со всеми точками прямой, лежащими между ними. Точки А и В называются концами отрезка, при этом порядок, в котором они берутся, не существен. Однако если отрезок АВ используется для графического изображения векторной величины, то порядок, в котором указаны концы отрезка, становится существенным. Пары точек АВ и В А задают один и тот же отрезок, но различные векторные величины.

В геометрии вектором называется направленный отрезок, т. е. отрезок, для которого указано, какая из концевых его точек считается первой, какая — второй. Первая точка направленного отрезка называется началом вектора, а вторая точка — концом.

Направление вектора на чертеже отмечается стрелкой, обращенной острием к концу вектора.

В тексте вектор записывается двумя заглавными буквами латинского алфавита со стрелкой наверху. Так, на рисунке 1,а изображены векторы АВ , CD , EF , GH , причем А, С, Е, G — соответственно начала, а В, D, F, Н — концы данных векторов. В некоторых случаях вектор обозначается также — одной строчной буквой, например, a , b , c (рис. 1,б)

При определении вектора мы предполагали, что начало вектора не совпадает с его концом. Однако в целях общности будем рассматривать и такие «векторы», у которых начало совпадает с концом. Они называются нулевыми векторами или нуль-векторами и обозначаются символом 0. На чертеже нуль-вектор изображается одной точкой. Если эта точка обозначена, например, буквой К, то нуль-вектор может быть обозначен также через КК .

1.1.3. КОЛЛИНЕАРНЫЕ ВЕКТОРЫ

Два вектора АВ и CD называются коллинеарными, если они лежат на одной и той же прямой или на параллельных прямых.

Нуль-вектор считается коллинеарным любому вектору.

На рисунке 1,а векторы АВ , CD , EF , GH попарно коллинеарны. На рисунке 2 векторы ЕС и DA коллинеарны, а АВ и ВС не коллинеарны.

Если ненулевые векторы АВ и CD коллинеарны, то они могут иметь одно и то же или противоположные направления. В первом случае их называют сонаправленными, во втором случае — противоположно направленными.

На рисунке 1,а векторы АВ и EF сонаправлены, а АВ и CD или АВ и GH противоположно направлены. В дальнейшем мы будем пользоваться следующими обозначениями: запись АВ || CD (или CD || АВ ) будет означать, что векторы АВ и CD коллинеарны; запись АВ ↓↓ CD (или АВ ↑↑ CD ) будет означать, что векторы АВ и CD сонаправлены, а запись АВ ↑↓ CD — что они имеют противоположные направления. Например, для векторов, изображенных на рисунке 1, а, имеют место соотношения: АВ ↓↓EF , АВ ↑↓ CD , GH ↓↓ CD , EF || GH , EF ↑↓ GH .

1.1.4. МОДУЛЬ ВЕКТОРА

Длиной или модулем ненулевого вектора называется длина отрезка, изображающего данный вектор. Длиной нулевого вектора называется число нуль. Длина вектора АВ обозначается символом | АВ |, или просто АВ (без стрелки наверху!). Длина вектора a обозначается так: | а | Очевидно, длина вектора a равна нулю тогда и только тогда, когда a — нулевой вектор. Вектор называется единичным, если его модуль равен единице.

1.1.5. РАВЕНСТВО ВЕКТОРОВ

Два вектора a и b называются равными, если выполнены следующие условия: а) модули векторов a и b равны; б) если векторы a и b ненулевые, то они сонаправлены.

Из этого определения следует, что два нулевых вектора всегда равны; если же один вектор нулевой, а другой отличен от нуля, то они не равны.

Равенство векторов a и b обозначается так: a = b .

Понятие равенства векторов обладает свойствами, которые аналогичны свойствам равенства чисел.

Теорема [1.1.] Равенство векторов удовлетворяет следующим условиям:

а) каждый вектор равен самому себе (условие рефлексивности);

б) если вектор a равен вектору b , то вектор b равен вектору a (условие симметричности);

в) если вектор a равен вектору b , а b равен вектору с , то a равен с (условие транзитивности).

1.1.6. ПЕРЕНОС ВЕКТОРА В ДАННУЮ ТОЧКУ

Пусть дан некоторый вектор a = EF и произвольная точка А. Построим вектор a, равный вектору a , так, чтобы его начало совпало с точкой А. Для этого достаточно провести через точку А прямую l , параллельную прямой EF, и отложить на ней от точки А отрезок AВ, равный отрезку EF. При этом точку В на прямой l следует выбрать так, чтобы векторы EF и АВ были сонаправлены. Очевидно, АВ есть искомый вектор a’ .

1.1.7. СУММА ДВУХ ВЕКТОРОВ

Суммой двух произвольных векторов a и b называется третий вектор р , который получается следующим образом: от произвольной точки О откладывается вектор a , от его конца А откладывается вектор b . Получившийся в результате этого построения вектор ОВ есть вектор р (рис. 3).

На рисунке 4 изображено построение суммы двух коллинеарных векторов: а) сонаправленных, б) противоположно направленных, в) векторов, из которых один нулевой, г) равных по модулю, но противоположно направленных (в этом случае, очевидно, сумма векторов равна нуль-вектору).

Легко видеть, что сумма двух векторов не зависит от выбора исходной точки О. В самом деле, если за исходную точку построения взять точку О’, то, как видно из рисунка 3, построение по указанному выше правилу дает вектор р’ , равный вектору р .

Очевидно также, что если a=a, и b=b,, то a+b=a,+b,

Из правила треугольника для сложения двух векторов вытекает простое и очень полезное для решения задач правило: каковы бы ни были три точки A, В и С, имеет место соотношение: АВ + ВС = АС .

Если слагаемые векторы не коллинеарны, то для получения их суммы можно пользоваться другим способом — правилом параллелограмма. На рисунке 5 дано построение суммы векторов a и b по этому правилу.

1.1.8. ОСНОВНЫЕ СВОЙСТВА СЛОЖЕНИЯ ВЕКТОРОВ

Теорема [1.2.] Понятие суммы векторов удовлетворяет следующим условиям:

а) для любых трех векторов a , b и c имеет место соотношение:

( a + b ) + c= a + ( b + c ) (ассоциативный закон);

б) для любых двух векторов a и b имеет место соотношение: a + b = b + a , т. е. сумма двух векторов не зависит от порядка слагаемых (коммутативный закон);

в) для любого вектора a , имеем: a+0 = a

г) для каждого вектора a существует противоположный вектор a, , т. е. вектор, удовлетворяющий условию: a + a, = . Все векторы, противоположные данному, равны между собой.

а) Пусть О — начало, а A —конец вектора a . Перенесем вектор b в точку A и от его конца В отложим вектор c , конец которого обозначим через С (рис.6). Из нашего построения следует, что OA=a , AB=b , BC=c (1).

Из правила треугольника имеем: ОС = ОВ + ВС и ОВ = ОА + АВ , поэтому ОС =( ОА + АВ )+ ВС . Подставив сюда значения слагаемых из (1), получаем: ОС = ( a + b ) + c

С другой стороны, ОС = ОА + АС и АС = АВ + ВС , поэтому ОС = ОА + ( АВ + ВС ). Подставив сюда значения слагаемых из (1), получаем: ОС = a + ( b + c ).

Из этого следует, что векторы ( a + b ) + c и a + ( b + c ) равны одному и тому же вектору ОС , поэтому они равны между собой.

г) Пусть a = ОА — данный вектор. Из правила треугольника следует, что ОА + АО = ОО = 0. Отсюда вытекает, что АО есть вектор, противоположный вектору a . Все векторы, противоположные вектору a = ОА , равны вектору АО , так как если каждый из них перенести в точку А, то концы их должны совпадать с точкой О в силу того, что a + a, = . Теорема доказана.

Вектор, противоположный вектору a , обозначается -a .

Из Теоремы [1.2.] следует, что если a 0, то -a =a и -a↓↑a . Также очевидно, что для любого вектора a имеем: -(- a )= a .

1.1.9. СЛОЖЕНИЕ НЕСКОЛЬКИХ ВЕКТОРОВ

Суммой трех векторов a , b и c будем считать вектор р = ( a + b ) + c . На основании ассоциативного закона (теорема[1.2]) сложения векторов р=a + ( b + c ), поэтому при записи суммы трех векторов мы можем опустить скобки и записать ее в виде a + b + c . Больше того, из теоремы [1.2] следует, что сумма трех векторов не зависит от порядка слагаемых.

Пользуясь доказательством теоремы [1.2], можно указать следующий способ построения суммы трех векторов a , b и c . Пусть О — начало вектора a . Перенесем вектор b в конечную точку вектора a , а вектор с — в конечную точку вектора b . Если С — конечная точка вектора с , то a + b + c = ОС (рис. 8).

Обобщая правило, данное для построения суммы трех векторов, можно указать следующее общее правило сложения нескольких векторов. Чтобы построить сумму векторов a1, a2 ,… an , достаточно вектор a2 перенести в конечную точку вектора a1 , затем вектор a3 перенести в конечную точку вектора a2 и т. д. Суммой данных векторов будет вектор, начало которого совпадает с началом вектора a1 , а конец — с концом an .

Сумма векторов a1, a2 ,… an обозначается: a1,+a2+ …+ an . На рисунке 9 дано построение суммы векторов a1, a2 , a3, a4 ,a5 :

ОА5 = a1,+a2+a3+ a4+a5 .

Указанное выше правило построения суммы нескольких векторов называется правилом многоугольника.

1.1.10. ВЫЧИТАНИЕ ВЕКТОРОВ

Вычитание вводится как операция, обратная сложению. Разностью векторов a и b называется такой вектор q , что q + b = a .

Разность векторов a и b обозначается так: a — b .

Таким образом, выражение q = a — b означает, что q + b = a .

Вектор a называется уменьшаемым, а вектор b — вычитаемым.

Теорема [1.3] Каковы бы ни были векторы a и b , всегда существует и единственным образом определяется разность a — b .

Доказательство. Возьмем произвольную точку О и перенесем векторы a и b , в эту точку. Если ОА = a и ОВ = b , то вектор ВА есть искомая разность, так как ОВ + ВА = ОА , или b + ВА = a . Данное построение выполнимо при любых векторах a и b , поэтому разность a — b всегда существует.

Теперь докажем, что разность определяется единственным образом. Пусть b + q = a и b + q’ = a . К обеим частям этих равенств прибавим вектор -b

Пользуясь теоремой [1.2], после элементарных преобразований получаем: q = a +( -b ), q’ = a +( -b ), поэтому q = q’ . Теорема доказана.

Следствия. 1°.Для построения разности двух векторов нужно эти векторы перенести в некоторую точку пространства. Тогда вектор, идущий от конца вычитаемого к концу уменьшаемого, есть искомый вектор.

2°. Для любых двух векторов a и b имеем: a — b = a +(- b), т. е. разность двух векторов равна сумме уменьшаемого вектора и вектора, противоположного вычитаемому.

1.1.11. МОДУЛИ СУММ И РАЗНОСТЕЙ ВЕКТОРОВ

Для произвольных векторов a и b имеют место следующие соотношения:

В соотношении а) знак равенства имеет место только в случае, если a↑↑b или если хотя бы один из векторов a и b нулевой.

В соотношении б) знак равенства имеет место только в случае, если a↑↓b или если хотя бы один из векторов a и b нулевой.

1.2. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

1.2.1. УМНОЖЕНИЕ ВЕКТОРА НА ЧИСЛО

Произведением ненулевого вектора a на действительное число α≠0 называется вектор р , удовлетворяющий следующим условиям:

а) | р | = | α | | a |, где | α | — модуль числа α ;

б) если α > 0, то р и a сонаправлены; если α р и a противоположно направлены.

Произведение нулевого вектора на произвольное число или произвольного вектора на число 0 равно нуль-вектору.

Произведение вектора a на число α обозначают так: αa или aα .

Легко видеть, что, каковы бы ни были α и a , их произведение есть вполне определенный вектор.

Лемма [2.1]. Для того чтобы вектор a был коллинеарен ненулевому вектору b , необходимо и достаточно, чтобы существовало число α , удовлетворяющее условию a = αb .

Доказательство. Пусть a коллинеарен ненулевому вектору b . Возможны следующие три случая: 1) a↑↑b, 2) a↑↓b , 3) a = 0.

Покажем, что в каждом из этих случаев существует число α , удовлетворяющее условию a = αb ,. В самом деле, в первом случае a=ab∙ b , т. е. α=ab . Во втором случае a=-ab∙b ,, поэтому α=-ab . В третьем случае a = 0 • b , α =0. Необходимость доказана.

Достаточность условия непосредственно следует из определения произведения вектора на число.

1.2.2. ОСНОВНЫЕ СВОЙСТВА

ПРОИЗВЕДЕНИЯ ВЕКТОРА НА ЧИСЛО

Теорема [2.2]. Для произвольных чисел α, β и векторов a, b имеют место следующие свойства:

а) 1 • a = a ; (-1) a = — a , где — a вектор, противоположный a ;

Свойство а) непосредственно следует из данного выше определения. Если хотя бы одно из чисел α,β равно нулю или хотя бы один из векторов a, b равен нулю, то справедливость остальных свойств очевидна, поэтому достаточно рассмотреть случай, когда α≠0,β≠0, a ≠0, b≠0 . Докажем свойства б) и г).

б). Пусть αβa = p1 и (αβ)a = р2 . Докажем, что p1 = р2 . Для этого необходимо убедиться в том, что векторы p1 и р2 имеют равные модули и сонаправлены.

Вычислим модули этих векторов:

| p1 |=| α || βa |=| α |(| β || a |) = | α || β || a |;

| р2 |=| αβ || a |==(| α || β |)| a |=| α || β || a |.

Таким образом, p1 = р2 . Векторы p1 и р2 по определению коллинеарны вектору a , поэтому они коллинеарны между собой.

Остается доказать, что p1 и р2 имеют одно и то же направление.

Возможны четыре случая:

Рассмотрим доказательства случаев 1) и 2).

1) α>0, β>0 . В этом случае по определению: a↑↑βa и βa↑↑p1 p1 = αβa , поэтому a↑↑α(βa) . С другой стороны, так как αβ>0 , то a↑↑αβa=р2 . Таким образом, p1 ↑↑ р2 , и в силу равенства их модулей p1 = р2 .

2) α>0, β . В этом случае a↓↑βa , βa ↑↑α(βa)= p1 , поэтому a↑↓ p1 . С другой стороны, так как αβ , то a↑↓(αβ)a = р2 . Итак, p1 ↑↑ р2 , поэтому p1 = р2 .

Доказательство свойства г). Пусть αa + b=p1 и αa +αb = р2 . Докажем, что p1 = р2 . Возможны два случая: 1)векторы a и b не коллинеарны; 2) векторы a и b коллинеарны. Рассмотрим каждый из этих случаев в отдельности.

1) Сначала предположим, что α>0 . Пользуясь правилом треугольника, построим сумму a + b . Пусть ОА = a , АВ = b , тогда ОВ = a + b (рис. 10). Пусть далее OP = p1. Так как α>0 , то точка Р лежит на луче ОВ. Проведем в плоскости ОАВ через точку Р прямую, параллельную АВ, и обозначим через Q точку пересечения этой прямой с прямой ОА. Так как треугольники ОАВ и OQP подобны, то α=OPOB=OQOA=QPAB .

Отсюда следует, что OQ = αa и QP = αb . Но OP = OQ + QP , поэтому p1=αa +αb=р2 .

2) Так как a и b коллинеарны, то из леммы [2.1] следует, что существует некоторое число λ , удовлетворяющее условию: a=λb , поэтому p1=αa +αb= α [( λb + b )] = α [( λ + 1) b ] = [ α ( λ + 1)] b . Здесь мы воспользовались свойствами б) и в).

Точно так же р2=αa +αb = α ( λb ) + αb = (αλ)b + αb =αλ+αb= [α (λ + 1)] b .

Поэтому p1 = р2 . Теорема доказана полностью.

1.3. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ

1.3.1. ЛИНЕЙНАЯ КОМБИНАЦИЯ ВЕКТОРОВ

Пусть на плоскости даны векторы a1, a2 ,… ak . Линейной комбинацией этих векторов называется всякий вектор вида α1a1+α2a2 +… + αkak , где α1, α2,…αk — произвольные числа.

Если все коэффициенты линейной комбинации равны нулю, то такая линейная комбинация называется тривиальной, в противном случае она называется нетривиальной. Легко видеть, что тривиальная линейная комбинация любого числа векторов есть нуль-вектор.

1.3.2. ЛИНЕЙНАЯ ЗАВИСИМОСТЬ ВЕКТОРОВ

В векторной алгебре всякое множество векторов, конечное или бесконечное, принято называть системой векторов. Система векторов a1, a2 ,… ak (1) называется линейно зависимой, если существуют такие числа λ1, λ2,…λk не равные нулю одновременно, что λ1a1+λ2a2 +… + λkak=0 , (2)

В противном случае система векторов называется линейно независимой. Другими словами, система (1) линейно независима, если из соотношения (2) следует, что λ1= λ2=…=λk = 0.

Определение линейной зависимости применимо также и в том случае, когда система состоит из одного вектора, т. е. когда k = 1. В этом случае, как легко видеть, система будет линейно зависимой тогда и только тогда, когда вектор системы нулевой.

Если система (1) линейно зависима, то в соотношении (2) по крайней мере один из коэффициентов не равен нулю. Пусть, например, λk 0. Разделив соотношение (2) на λk , получаем: ak=-λ1λka1-λ2λka2-…-λk-1λk ak-1

В этом случае вектор ak является линейной комбинацией векторов a1, a2 ,… ak-1. Говорят также, что вектор ak линейно выражается через векторы a1, a2 ,… ak-1 . Итак, если система линейно зависима, то хотя бы один из векторов этой системы линейно выражается через другие.

Докажем вспомогательное предложение.

Лемма [3.1]. Если часть данной системы линейно зависима, то вся система также линейно зависима.

Доказательство. Пусть (1) — данная система. Допустим, например, что система векторов a1, a2 ,… al , где l , линейно зависима α1a1+α2a2 +… + αlal=0 . По определению хотя бы один из коэффициентов α1, α2,…αl не равен нулю. Это соотношение можно переписать так: α1a1+α2a2 +…+ αlal+0∙al+1+…+ 0∙ak = 0. Мы видим, что система (1) также линейно зависима.

1.3.3. СИСТЕМА КОЛЛИНЕАРНЫХ ВЕКТОРОВ

Конечная или бесконечная система векторов называется коллинеарной, если любые два вектора этой системы коллинеарны. Например, векторы АВ , CD , EF , GH на рисунке 1, а (стр. 4) образуют коллинеарную систему, а векторы BE , ВС , AD , DC на рисунке 2 не образуют коллинеарной системы.

Отметим, что если система коллинеарна, то всякая ее часть также коллинеарна. В частности, если бесконечная система векторов коллинеарна, то всякая ее конечная часть коллинеарна.

Рассмотрим один частный, но весьма важный случай бесконечной системы коллинеарных векторов. Возьмем в пространстве прямую и рассмотрим множество всех векторов пространства, параллельных этой прямой. Это множество, очевидно, образует коллинеарную бесконечную систему векторов. Эта система называется одномерным векторным подпространством.

Итак, одномерное векторное подпространство — это совокупность всех векторов пространства, параллельных некоторой прямой l . Следует подчеркнуть, что любое одномерное векторное подпространство содержит нуль-вектор. Очевидно, каждое одномерное векторное подпространство имеет хотя бы один ненулевой вектор е , через который линейно выражается любой вектор подпространства. В случае подпространства, в отличие от общего случая системы коллинеарных векторов, для любого действительного числа α вектор р=αе , принадлежит подпространству.

Таким образом, одномерное векторное подпространство есть множество векторов вида αе при всевозможных значениях α .

1.3.4. СИСТЕМА КОМПЛАНАРНЫХ ВЕКТОРОВ

По аналогии с предыдущим введем следующее определение: конечная или бесконечная система векторов называется компланарной, если в пространстве существует плоскость, которой параллельны все векторы системы (2). На рисунке 11 векторы ОА1, ОА2 , А3А , А2В образуют компланарную систему. Векторы ОЕ1 , ОЕ2 , ОЕ3 не образуют компланарной системы. Легко видеть, что любая система, состоящая из двух векторов, всегда компланарна. Далее, если некоторая система компланарна, то любая ее часть также компланарна. Если все векторы компланарной системы перенести в одну точку О пространства, то, очевидно, их концы А вместе с точкой О будут лежать в одной плоскости. Этим по существу объясняется термин «компланарность», что означает принадлежность одной и той же плоскости.

Рассмотрим один частный, но весьма важный случай бесконечной системы компланарных векторов. Возьмем в пространстве некоторую плоскость π и рассмотрим множество всех векторов пространства, параллельных этой плоскости. Это множество, очевидно, образует компланарную систему векторов, которая называется двумерным векторным подпространством. Итак, двумерное векторное подпространство — это совокупность всех векторов пространства, параллельных некоторой плоскости π . Отметим, что любое двумерное подпространство, так же как и одномерное, содержит нуль-вектор.

1.3.5. БАЗИС СИСТЕМЫ КОМПЛАНАРНЫХ ВЕКТОРОВ

Теорема [3.2]. Если конечная или бесконечная система компланарных векторов содержит хотя бы два неколлинеарных вектора е1 и е2 , то любой вектор a этой системы линейно выражается через е1 и е2 , т. е. a = αе1 + βе2 (3), где α и β — действительные числа.

Любая конечная система компланарных векторов, состоящая более чем из двух векторов, линейно зависима.

Доказательство. Пусть a — произвольный вектор системы (1). Перенесем векторы a , е1 и е2 в произвольную точку О пространства и обозначим через A, E1 , Е2 их концы. В силу компланарности данной системы точки О, E1 , Е2 и А лежат в одной плоскости. Но векторы е1 и е2 не коллинеарны, поэтому О, E1 и Е2 не лежат на одной прямой (рис. 12).

Проведем через точку А прямые, параллельные векторам е1 и е2 . Обозначим через А1 и А2 точки пересечения этих прямых соответственно с прямыми ОE1 и ОЕ2 . Очевидно, ОА = ОА1 + ОА2 . С другой стороны, векторы ОА1 и е1 , ОА2 и е2 коллинеарны и е1≠0 , е2≠0 , поэтому существуют такие α≠0, β≠0, что ОА1 = αе1 , ОА2=βе2 . Подставив эти выражения в предыдущее соотношение, получим (3).

Теперь докажем вторую часть теоремы. Пусть (1)—данная система и k > 2 . Если векторы a1 и a2 коллинеарны, то они линейно зависимы, поэтому согласно лемме [3.1] система (1) линейно зависима. Если a1 и a2 не коллинеарны, то согласно первой части теоремы имеем: a3 = α1a1 + β1a2 . Мы видим, что часть системы (1) линейно зависима, следовательно, согласно лемме [3.1] вся система линейно зависима.

Введем следующее определение: базисом системы компланарных векторов называется совокупность любых двух неколлинеарных векторов этой системы, взятых в определенном порядке.

Предыдущая теорема показывает, что любой вектор компланарной системы линейно выражается через базис.

Легко видеть, что каждое двумерное векторное подпространство содержит хотя бы два неколлинеарных вектора, т. е. базис. Из теоремы [3.2] следует, что любой вектор a этого подпространства линейно выражается через е1 и е2 . В случае подпространства, в отличие от общего случая системы компланарных векторов, вектор a , имеющий вид (3), при любых действительных α и β принадлежит подпространству. Таким образом, если е1 , е2 — базис двумерного подпространства, то это подпространство есть множество векторов a вида (3) при всевозможных действительных значениях α и β .

Теорема [3.3]. Для того чтобы три вектора a1 , a2 , a3 были компланарны, необходимо и достаточно, чтобы они были линейно зависимы.

Доказательство. В самом деле, если система векторов a1 , a2 , a3 компланарна, то согласно теореме [3.2] она линейно зависима.

Обратно, пусть система линейно зависима : α1a1+α2a2 + α3a3=0

Если, например, α3≠0 , то из данного соотношения получаем:

a3=-α1α3∙a1-α2α3 ∙ a2. Если π — некоторая плоскость, параллельная векторам a1 и a2 , то отсюда видно, что a3 является вектором, параллельным той же плоскости.

ГЛАВА 2 МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ

2.1 ВЕКТОРЫ В ШКОЛЬНОМ КУРСЕ ГЕОМЕТРИИ

Далее в дипломной работе я рассматриваю векторы в школьном курсе геометрии на основе учебников геометрии для общеобразовательных учреждений следующего коллектива авторов: Л. С. Атанасян, В. Ф. Бутузов, С. Б. Кадомцев и др.

Понятие вектора и действия над векторами вводятся в 9 классе( в 8 классе – 2-ой вариант программы), так, как это принято в физике. Величины, которые характеризуются не только числовым значением, но и направлением, называются в физике векторными и изображаются отрезками со стрелкой. Поэтому геометрический вектор вводится как направленный отрезок, т.е. отрезок на котором дано направление от одного конца к другому.

На изучение главы «Векторы», в которой рассматриваются 3 учебные темы, отводится 8 часов(12 часов – 2 вариант программы).

Основная цель изучения темы «Векторы» в 8-9 классах — научить обучающихся выполнять действия над векторами как направленными отрезками, что важно для применения векторов в физике; познакомить с использованием векторов при решении геометрических задач.

Основное внимание уделяется выработке умений выполнять операции над векторами (складывать векторы по правилам треугольника и па раллелограмма, строить вектор, равный разности двух данных векторов, а также вектор, равный произведению данного вектора на данное число):

На примерах показывается, как векторы могут применяться к решению геометрических задач.

В результате изучения данной главы в основной школе учащиеся приобретают следующие знания и умения, соответствующие требованиям стандарта основного общего образования (Таблица 1).

На изучение главы «Векторы в пространстве» отводится 6 часов. При изучении геометрии на базовом уровне (1-ый вариант программы – 51 час в год) данную тему проходят в 4 четверти в 10 классе, а при изучении геометрии на профильном уровне (2-ой вариант программы – 68 часов в год) данную тему проходят в 1 четверти в 11 классе.

Основная цель изучения темы «Векторы в пространстве» в 10-11 классах — закрепить известные учащимся из курса планиметрии сведения о векторах и действиях над ними, ввести понятие компланарных векторов в пространстве и рассмотреть вопрос о разложении любого вектора по трём некомпланарным векторам.

Основные определения, относящиеся к действиям над векторами в пространстве, вводятся так же, как и для векторов на плоскости. Поэтому изложение этой части материала является достаточно сжатым. Более подробно рассматриваются вопросы, характерные для векторов в пространстве: компланарность векторов, правило параллелепипеда сложения трёх некомпланарных векторов, разложение вектора по трём некомпланарным векторам.

В результате изучения данной главы в средней школе учащиеся приобретают следующие знания и умения, соответствующие требованиям стандарта среднего общего образования (Таблица 2).

Источник

Решение задач векторным способом 9 класс