Решение задач способом вспомогательных секущих плоскостей

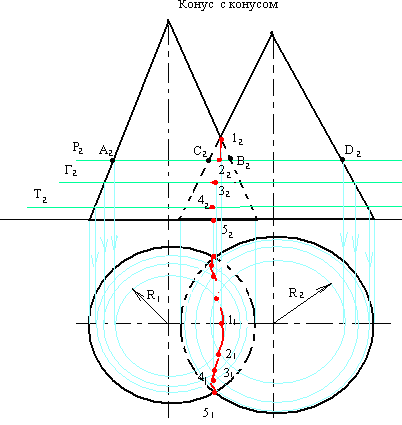
Способ вспомогательных секущих плоскостей

Суть способа – вспомогательная секущая плоскость одновременно пересекает поверхности каждого тела и образует фигуры сечения, контуры которых пересекаются. Точки пересечения контуров соединяют.

Этот способ применим тогда, когда контуры отдельных сечений представляют прямые линии или окружности.

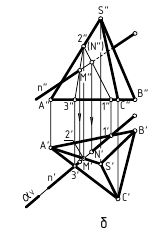
Точки 1 (1₂₎, 5 ( 5₁) и 5 / (5₁ / ) являются очевидными – это точки пересечения очерковых и оснований конусов. Найдём соответствующие вторые проекции этих точек.

Проведём горизонтальную плоскость Р₂, которая рассечет оба конуса. В сечении конусов будут окружностиR₁= А₂В₂/2 иR₂ = С₂D₂/2 , причем их фронтальными проекциями являются прямые. Построим горизонтальные проекции этих сечений – окружности радиусомR₁иR₂.

На пересечении этих окружностей сечений на П₁определим горизонтальную проекцию общей точки – 2₁(2₁ / ). Фронтальную проекцию точек 2 и 2 / определим по линиям связи на секущей плоскости Р₂.

Проведём еще ряд горизонтальных секущих плоскостей и определим проекции других промежуточных точек линии пересечения, которые соединим лекальной кривой с учётом видимости.

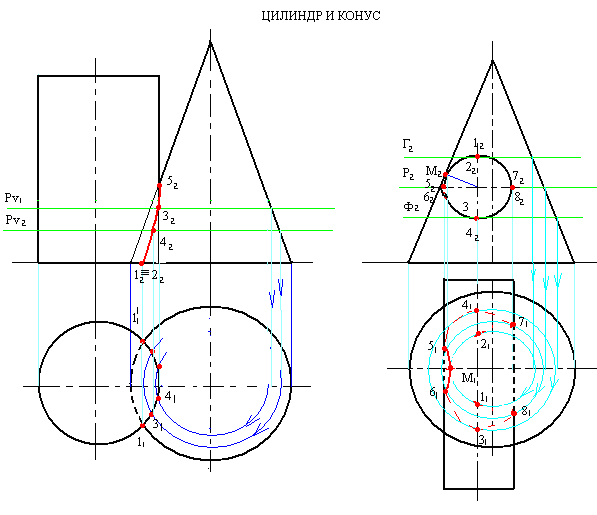
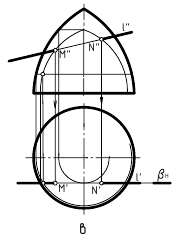
При взаимном пересечении конуса и цилиндра (рисунок 1) ось вращения цилиндра перпендикулярна П₂. Значит, на П₂линия пересечения совпадет с контуром основания цилиндра, т.е. фронтальной проекцией линии пересечения будет являться фронтальная проекция цилиндра.

Построив горизонтальную проекцию линии пересечения, на П₂на пересечении горизонтальной оси симметрии цилиндра с проекцией цилиндра наметим точки 5₂, 6₂, 7₂, 8₂– точки границы видимости линии пересечения, лежащие на экваторе цилиндра.

На П₁точки линии пересечения, лежащие выше экватора будут видимы, а точки, лежащие ниже экватора – невидимы.

Способ вспомогательных сфер

Этот метод можно применять при соблюдении следующих условий :

— пересекающиеся поверхности должны быть поверхностями вращения;

— их оси должны пересекаться ; точка пересечения осей является центром вспомогательных сфер;

— их оси должны быть // какой-либо плоскости проекций.

Сфера R_min должна касаться образующей большего тела, а меньшее тело – пересекать.

Сфера R_min определяется как большее расстояние от центра сфер до образующих обоих тел — перпендикуляры из центра сфер к очерковым образующим. Больший перпендикуляр и будет являться радиусом минимальной сферы.

Сфера пересекает тела по окружностям, проецирующимся на одну из плоскостей проекций отрезком.

1. Определяем очевидные точки 12(11) и 22(21)

2. Восстанавливаем перпендикуляры из центра сфер О₂к очерковым образующим цилиндра и конуса. Перпендикуляр к цилиндру О₂F₂ больше, чем перпендикуляр к образующей конуса. Значит, О₂F₂=Rи будет являться радиусом минимальной сферы. На П₂проводим из центра О₂этим радиусомRокружность, которая рассечет и конус и цилиндр по окружностям, фронтальной проекцией которых будут прямые – сечение конуса А₂В₂и сечение цилиндра С₂F₂.

На пересечении этих сечений определяем фронтальную проекцию точки 3 – 3₂.

3. На П₁строим горизонтальную проекцию сечения конуса, на котором находится точка 3 – окружность радиусом А₂В₂/ 2, на которой по линии связи определяем точки 3₁и 3₁ / .

Проводим ещё ряд секущих сфер радиусом больше минимальной и меньше максимальной и определяем другие промежуточные точки линии пересечения, которые соединяем лекальной кривой с учётом видимости.

Большее тело поглощает меньшее.

Видимость линии пересечения определяем следующим образом:

— на пересечении фронтальной проекции линии пересечения с осью симметрии цилиндра намечаем точку К₂(К₁и К₁ / определяем на П₁на очерковых образующих цилиндра);

— часть линии, находящаяся выше точки К – видимая. Точка К – граница видимости.

Вопросы для самопроверки

В чем заключается метод вспомогательных секущих плоскостей?

В чем заключается метод вспомогательных секущих сфер?

Источник

Решение задач способом вспомогательных секущих плоскостей

Простейшая позиционная задача с использованием этого метода — оценка взаимного расположения прямой и плоскости. Сущность метода заключается в следующем: через прямую проведем вспомогательную секущую плоскость g и установим относительное положение двух прямых а и в , последняя из которых является линией пересечения вспомогательной секущей плоскости g и данной плоскости a (рис.150).

Рисунок 1 50. Метод вспомогательных секущих плоскостей

Каждому из трех возможных случаев относительного расположения этих прямых соответствует аналогичный случай взаимного расположения прямой и плоскости. Так, если обе прямые совпадают, то прямая а лежит в плоскости a , параллельность прямых укажет на параллельность прямой и плоскости и, наконец, пересечение прямых соответствует случаю, когда прямая а пересекает плоскость a .

Таким образом возможны три случая относительного расположения прямой и плоскости:

Вспомогательные секущие плоскости чаще всего выбирают перпендикулярными или параллельными плоскости проекций.

Этот способ рекомендуется применять, если сечения заданных поверхностей одной и той же плоскостью являются прямыми линиями или окружностями. Такая возможность существует в трех случаях:

если образующие (окружности) расположены в общих плоскостях уровня;

если в общих плоскостях уровня оказываются прямолинейные образующие линейчатой поверхности и окружности циклической;

линейчатые каркасы заданных поверхностей принадлежат общим плоскостям уровня или пучкам плоскостей общего положения.

Источник

Метод вспомогательных секущих плоскостей

Для построения линии пересечения двух поверхностей часто применяют метод вспомогательных секущих плоскостей. Смысл этого метод заключается в том, что вводят дополнительную секущую плоскость, которая пересекает обе поверхности. Затем строят линии пересечения обеих поверхностей секущей плоскостью. Точка пересечения этих линий и есть общая точка этих поверхностей. Пересекая поверхности рядом дополнительных плоскостей, получают множество точек, общих для пересекающихся поверхностей.

Как выбрать положение или вид этих вспомогательных плоскостей?

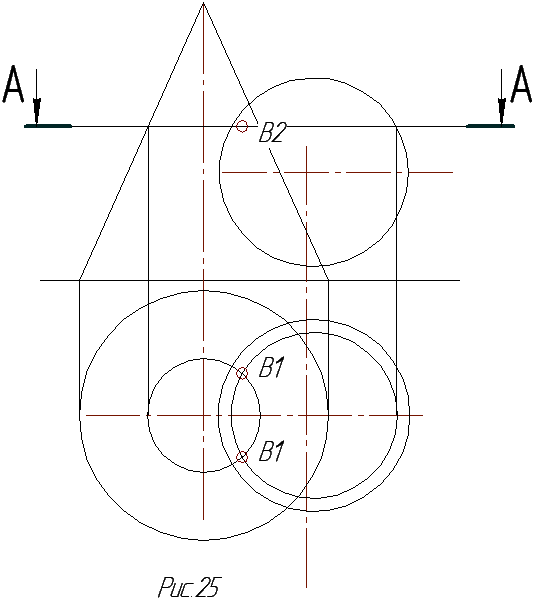
Дополнительные плоскости подбирают таким образом, чтобы они в пересечении с поверхностями давали простые линии пересечения, например, окружности или прямые. Кроме того, эти линии при проецировании на плоскости проекций, должны проецироваться в натуральную величину. Для этих целей подходят обычно плоскости уровня. Рассмотрим на примере работу с одной плоскостью, которую выберем перпендикулярно оси вращения конуса (рис.25).

При решении задач по построению линии пересечения поверхностей необходимо находить характерные точки линии пересечения. Эти точки, как правило, являются точками пересечения очерковых образующих, если поверхности имеют общую ось симметрии, как в примере, рассмотренном на рис.25. Так как эти точки лежат на очерке (точки С и К), то их горизонтальные проекции лежат на оси симметрии поверхностей (рис.26).

Источник

Метод плоскостей | AutoCAD

В этом уроке рассмотрим одну из самых распространенных задач начертательной геометрии – построение пересечения поверхностей методом секущих плоскостей и способ ее решения средствами AutoСАD.

Метод секущих плоскостей, немного теории

Вкратце суть метода секущих плоскостей состоит в том, что для построения линии пересечения двух поверхностей строятся вспомогательные плоскости (обычно – параллельные одной из плоскостей проекций), которые пересекают заданные поверхности, образуя при этом простые геометрические фигуры.

Точки взаимного пересечения заданных поверхностей будут общими точками двух кривых, образованных пересечением секущей плоскости с каждой из поверхностей.

Условия задачи

Зададим условия: пусть необходимо построить пересечение полусферы и конуса, расположенных таким образом:

Размеры показаны для наглядности, проставлять их на чертеже не нужно.

Решение

Строим секущие плоскости, вид с боку

Очевидно, что для тел вращения удобно использовать плоскости, перпендикулярные осям этих тел. В нашем случае вспомогательные плоскости будут параллельными горизонтальной плоскости. Изобразим их на фронтальном виде (в нашем случае верхняя из плоскостей проходит через явно видимую верхнюю точку пересечения конуса и полусферы, в других случаях для нахождения этой точки потребуются дополнительные построения):

Секущие плоскости, вид сверху

Теперь перенесем линии пересечения секущих плоскостей с каждой из поверхностей на вид сверху. Очевидно, что горизонтальные плоскости пересекают каждое из тел по окружностям, центры которых находятся на одной вертикали с центрами тел. Радиусы этих окружностей легко переносятся на вид сверху с образующих каждой поверхности. Вот эти окружности для полусферы:

Точки пересечения секущих плоскостей

Отметим для наглядности общие точки для каждой из пар окружностей, образованных одной плоскостью:

Видно, что в районе верхней точки построение недостаточно «информативно», т.е. будет полезным построить еще одну секущую плоскость:

Вот еще две точки, заданные этой плоскостью:

Линия пересечения

Соединив на виде сверху полученные точки сплайном (команда Сплайн), мы получим приближенную линию пересечения двух поверхностей:

Остается перенести линию на фронтальный вид. Сделать это совсем несложно: нужно перенести каждую из точек с вида сверху на соответствующую секущую плоскость на фронтальном виде. Линии построения выделены желтым цветом:

Поскольку исходные поверхности (и, соответственно, линия их пересечения) симметричны относительно плоскости, параллельной фронтальной плоскости проекции, достаточно перенести только половину точек. В нашем частном случае невидимая на фронтальном виде часть кривой «спрятана» за видимой, а верхняя точка является точкой разделения видимой и невидимой частей.

Проверка вида линии пересечения

Полезно проверить правильность наших построений средствами 3D-моделирования. Построим соответствующие фигуры, перейдя предварительно к интерфейсу 3D- моделирование , и сравним полученную модель с построением (для этого удобнее объединить объекты командой Объединить).

Резюме

Как видим, наше построение довольно точно передает реальную линию пересечения поверхностей вращения. И хотя современные средства моделирования позволяют строить такие пересечения гораздо быстрее, рассмотренные нами принципы очень полезны для понимания «механики» геометрических построений, без которого любой, даже самый современный инструмент 3D-моделирования превращается в сложную и непонятную игрушку.

Источник

Построение линии пересечения поверхностей с примерами

Содержание:

Построение линии пересечения поверхностей:

Предложенные задания охватывают задачи не на все методы построения линий пересечения поверхностей, а только наиболее распространенные. Ниже приведены решения типовых задач, когда применены различные способы в зависимости от формы и расположения пересекающихся поверхностей.

Одна из поверхностей занимает частное (проецирующее) положение

Задание: даны две поверхности:

Решение: поверхность цилиндра перпендикулярна к

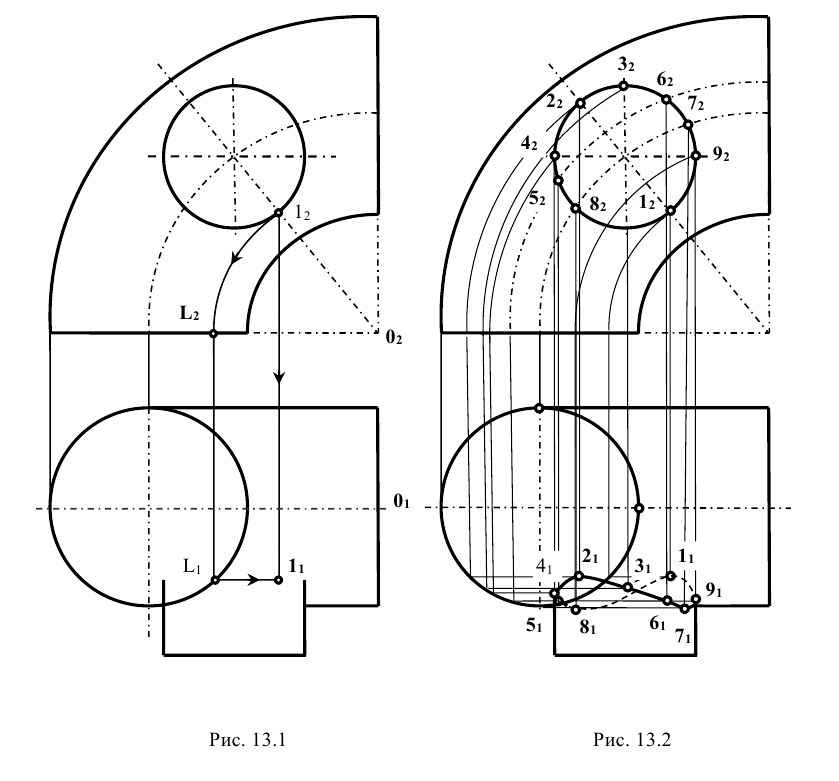
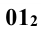
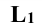
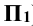
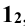
Ниже приводится построение горизонтальной проекции только одной точки 1 (рис. 13.1). Из этой точки вниз проводят линию проекционной связи. Одновременно из этой же точки радиусом проводят дугу окружности, на которой лежит эта точка, как принадлежащая тору, и находят проекцию этой окружности на горизонтальной проекции тора — это прямая линия, параллельная оси x. Она проходит через точку (точка пересечения окружности, проходящей через точку 1, с окружностью тора, лежащей на ). Горизонтальная проекция точки 1 находится на пересечении линии проекционной связи, проведенной из точки , с горизонтальной проекцией окружности тора, на которой лежит точка 1. Остальные точки строят аналогично точке 1 (рис. 13.2).

Точки 4 и 9 определяют видимость линии пересечения на горизонтальной проекции, а точки 1 и 2 наиболее удаленные от контура на горизонтальной проекции. Эту задачу можно решать и методом вспомогательных секущих плоскостей, который рассматривается далее.

Метод вспомогательных секущих плоскостей

Этот метод применяется для построения линии пересечения двух поверхностей, когда секущие (параллельные) плоскости при пересечении с данными поверхностями образуют простые для построения линии (прямую или окружность).

Задание: даны поверхности конуса 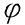и цилиндра Ф (рис. 13.3). Требуется построить линию их пересечения.

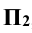
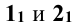
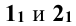
Решение: ось цилиндра перпендикулярна к плоскости , следовательно, поверхность цилиндра — проецирующая. В этом случае задача может быть решена так, как это было разобрано в предыдущем (п. 13.1.1) примере. Для этого определяют характерные -наивысшую и низшую точки линии пересечения 1 и 2, лежащие на пересечении фронтальной проекции цилиндра с очерковой образующей конуса. Их горизонтальные проекции принадлежат горизонтальной проекции очерковой образующей конуса (, совпадают с осевой линией конуса). Точки 3 и 4 определяют видимость линий пересечения на горизонтальной проекции.

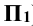
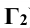
Для определения их горизонтальных проекций через ось цилиндра параллельно проводят вспомогательную секущую плоскость Г (ее фронтальный след ).

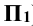
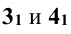
Эта плоскость рассечет цилиндр по очерковым образующим, а конус по окружности радиуса R, которая на будет проецироваться в натуральную величину. Пересечение этой окружности с очерковыми образующими цилиндра есть не что иное, как горизонтальные проекции характерных точек (рис. 13.3).

Построение промежуточных точек аналогично построению точек 3 и 4, только образующие, по которым вспомогательная плоскость будет рассекать цилиндр, не будут очерковыми (рис. 13.4).

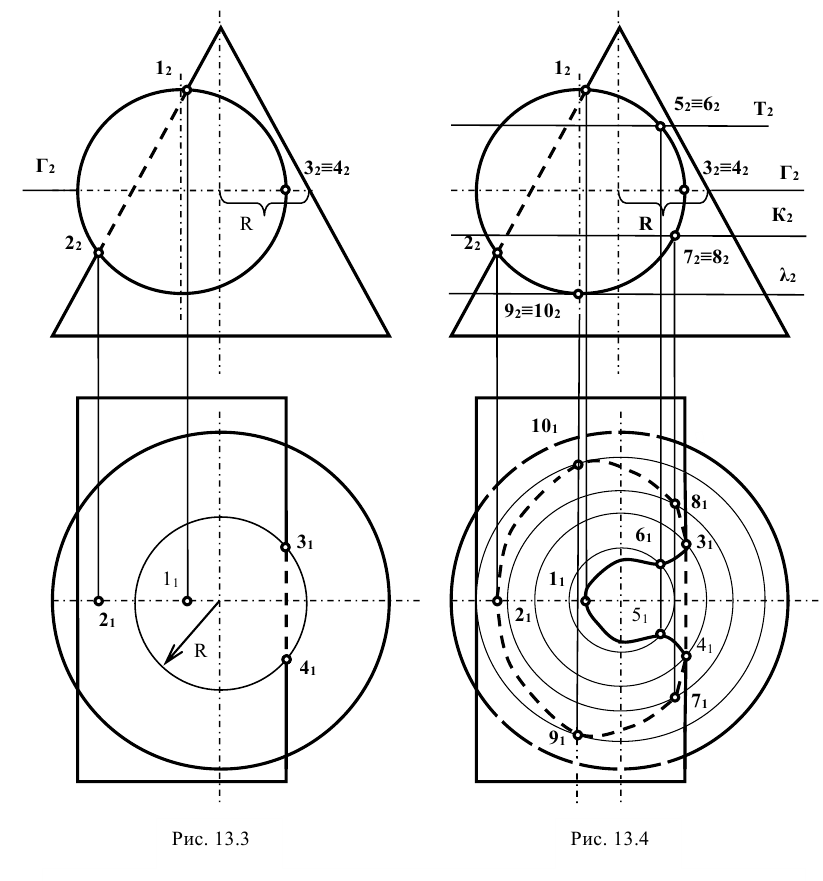
Задание: Даны две поверхности вращения — конус и цилиндр, оси которых пересекаются и находятся в одной плоскости, параллельной 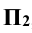(рис. 13.5). Требуется построить линию их пересечения.

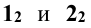
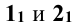
Решение: на фронтальной проекции фиксируют точки пересечения заданных поверхностей вращения — они принадлежат искомой линии пересечения. Горизонтальные проекции этих точек находятся на осевой линии конуса и цилиндра – .

Другие точки линии пересечения можно построить, используя концентрические сферические поверхности. Из точки пересечения осей фронтальных проекций, как из центра, проводятся сферы. Первая — касательная к проекции конуса, а последующие — большим радиусом (рис. 13.6). Каждая сфера пересекает обе поверхности по окружностям, фронтальные проекции которых изображаются отрезками прямых линий. Эти проекции пересекаются в точках, являющихся фронтальными проекциями точек искомой линии пересечения поверхностей.

Горизонтальные проекции этих точек определяются по принадлежности одной из поверхностей. В данном случае удобнее их получать по принадлежности конусу. Например, точки 3 и 4 лежат на той же окружности, по которой вспомогательная сфера пересекает конус. Изменяя радиус вспомогательной секущей сферы, находят ряд точек линии пересечения, соединив которые, получают проекции искомой линии (рис. 13.6). Чтобы определить видимость горизонтальной проекции линии пересечения, на её фронтальной проекции отмечают точки, лежащие на проекции осевой линии цилиндра и принадлежащие линии пересечения.

Затем по линиям проекционной связи переносят их на очерковые образующие горизонтальной проекции цилиндра. Точки, лежащие ниже указанных, будут находиться на невидимой части цилиндра.

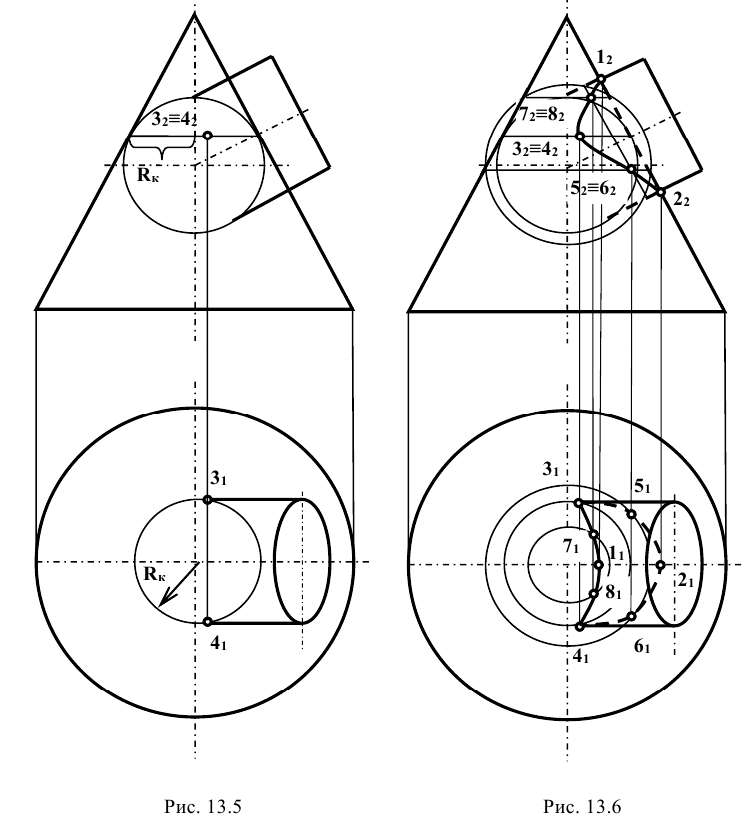
Метод эксцентрических сфер

Метод эксцентрических сфер применяется для построения линии пересечении поверхностей вращения, у которых оси расположены в одной плоскости, являющейся плоскостью симметрии. При этом пересекающиеся поверхности должны иметь семейство круговых сечений.

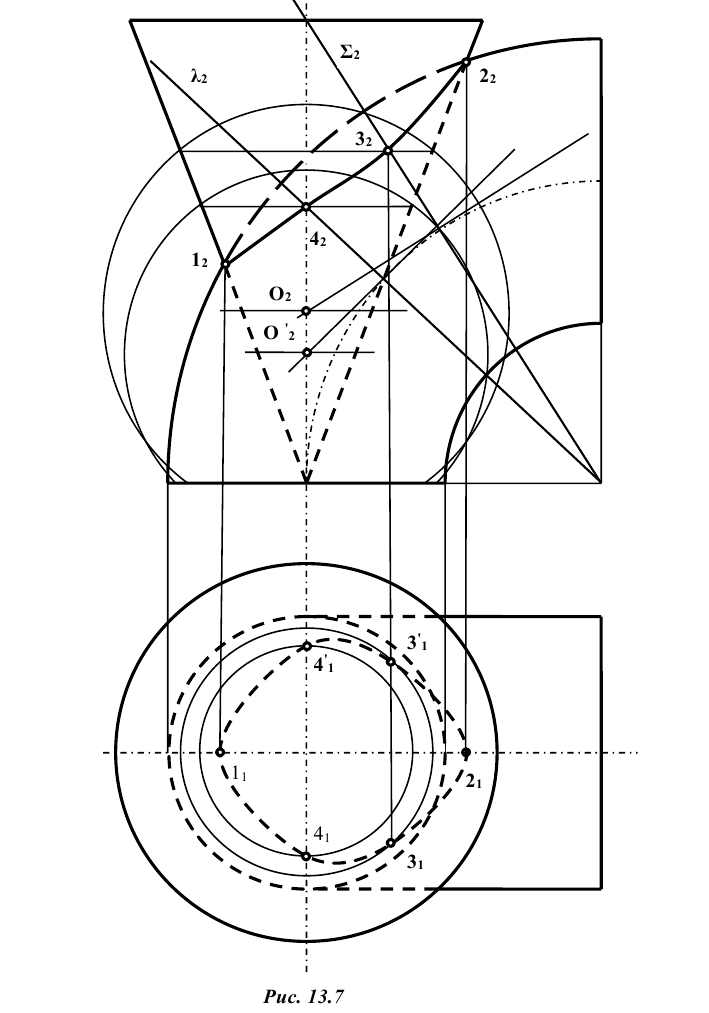
Задание: даны две поверхности вращения — тор и конус, оси которых находятся в одной плоскости, параллельной 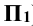(рис. 13.7). Требуется построить линии их пересечения.

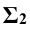
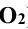
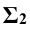
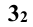
Решение: прежде всего, фиксируют опорные точки пересечения очерковых меридианов 1 и 2. Затем через ось вращения поверхности кольца проводят фронтальный след фронтально проецирующей плоскости Σ. Линия пересечения её с поверхностью тора — окружность. Центр сферы, пересекающей кольцо по окружности, находится на перпендикуляре, восстановленном из центра такой окружности к секущей проецирующей плоскости. Чтобы конус пересекался вспомогательной секущей сферой по окружности, её центр должен находиться на оси конуса. Точка пересечения перпендикуляра к проецирующей плоскости с осью конуса () выбирается центром вспомогательной секущей сферы. Радиус ее равен расстоянию от центра до точки пересечения меридиана тора со следом плоскости . Такая вспомогательная секущая сфера пересекает кольцо и конус вращения по окружностям, фронтальные проекции которых — проекции прямых. Точка пресечения этих отрезков (рис. 13.7) принадлежит искомой линии пересечения поверхностей.

Вспомогательные сферы имеют различные центры на оси конуса вращения; так, при построении проекции — точки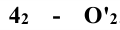. Горизонтальные проекции точек пересечения строят по принадлежности этих точек к одной из поверхностей, используя параллели, например, конуса.

Пересечение линии с поверхностью

В общем случае для графического определения положения точек пересечения линии с поверхностью необходимо выполнить ряд геометрических построений в следующей последовательности: заключить линию во вспомогательную поверхность; определить линию пересечения этой поверхности с заданной поверхностью; отметить точки пересечения построенной линии с заданной.

Этот алгоритм является универсальным, пригодным для решения любых задач. Ранее (лекция 4, рис. 4.5 и 4.6) он применялся для построения проекций точки пересечения прямой с плоскостью, где в качестве вспомогательной секущей поверхности использовалась плоскость и строилась прямая линии пересечения ее с заданной плоскостью, а искомая проекция точки пересечения определялась как место пересечения этой линии с заданной прямой.

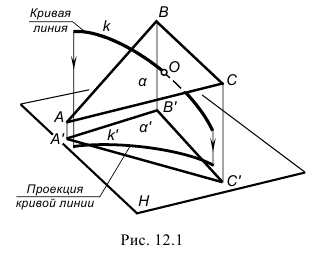
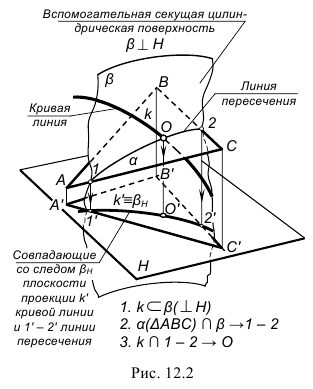
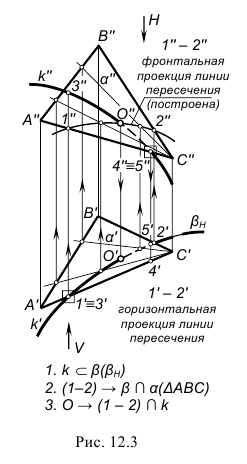
На рис. 12.1–12.3 проиллюстрирован тот же алгоритм применительно к построению точки пересечения кривой линии k с плоскостью α(∆ABC).

В качестве секущей поверхности в данном случае следует использовать проецирующую цилиндрическую поверхность, в частности, горизонтально-проецирующую β(β_H)H, в которую должна быть заключена кривая k(k»,k’). Для этого на чертеже (рис. 12.3) обозначаем горизонтальный след этой поверхности β_H. Горизонтальная проекция линии ее пересечения с заданной плоскостью α(∆ABC) совпадает с ним, располагаясь между точками 1′-2′. Для построения ее фронтальной проекции воспользуемся произвольными вспомогательными прямыми линиями, принадлежащими плоскости. Вначале задаем их горизонтальные проекции, например, через вершину C. Затем по точкам их пересечения со стороной AB находим фронтальные проекции вспомогательных прямых и определяем на них фронтальные проекции точек пересечения с ними заданной кривой. Проводим через найденные точки плавную кривую линию, являющуюся, таким образом, фронтальной проекцией линии пересечения, и отмечаем на ней место пересечения с фронтальной проекцией заданной кривой k(k»,k’) – точку O». Это и будет фронтальная проекция искомой точки пересечения заданной кривой k(k»,k’) с плоскостью α(∆ABC). Затем, воспользовавшись линией связи, находим горизонтальную проекцию O’ точки пересечения.

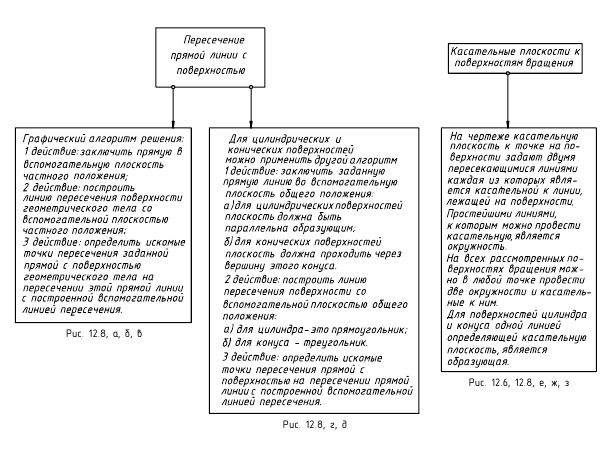
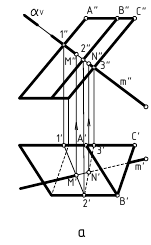
Этот алгоритм применен и для построения точек пересечения прямой линии с поверхностями геометрических тел – призмы, пирамиды и самопересекающегося тора (рис. 12.8, а, б, в). Поскольку поверхности этих тел являются замкнутыми, то необходимо найти по две точки пересечения на каждой из них.

При пересечении с призмой (рис. 12.8, а) в качестве секущей плоскости для заключения в нее заданной прямой m(m»,m’) использовалась фронтально-проецирующая плоскость α_V. При пересечении с пирамидой (рис. 12.8, б) в качестве секущей плоскости для заключения в нее заданной прямой n(n»,n’) использовалась горизонтально-проецирующая плоскость α_H. При пересечении с самопересекающимся тором (рис. 12.8, в) в качестве секущей плоскости для заключения в нее заданной прямой l(l»,l’) использовалась фронтальная плоскость β_H. Далее все действия аналогичны рассмотренным. В каждом случае вначале строилась линия пересечения поверхности плоскостью, исходя из ее проецирующего положения, определялись на ней точки пересечения с заданной прямой, а при окончательном оформлении – видимость на чертеже.

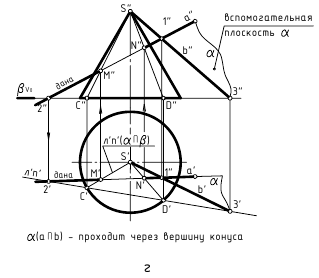
В качестве секущей плоскости при определении точек пересечения прямой с поверхностью могут использоваться также плоскости общего положения, пересекающие поверхность вдоль ее образующих (рис. 12.8, г, д). Так, для построения точек пересечения прямой a(a»,a’) общего положения с поверхностью прямого кругового конуса (рис. 12.8, г) показано использование плоскости общего положения α, проходящей через вершину конуса и заданную прямую. Плоскость задана двумя пересекающимися прямыми. Одна из них – это заданная прямая a(a»,a’), вторая – пересекающаяся с ней произвольная прямая b(b»,b’), проходящая через вершину конуса. Для построения проекций образующих, вдоль которых плоскость пересекает поверхность конуса, найден ее горизонтальный след, затем проекции C’ и D’ точек его пересечения с горизонтальным следом основания конуса и фронтальные проекции C» и D» этих точек. Искомые проекции точек M(M»,M’) и N(N»,N’) пересечения заданной прямой общего положения с поверхностью конуса находятся в местах пересечения с ней построенных образующих.

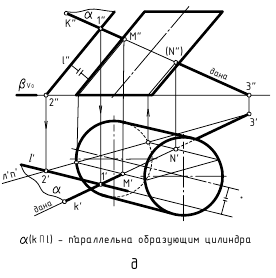
Аналогичные действия выполнены и для построения проекций M»,M’ и N»,N’ точек пересечения прямой общего положения k(k»,k’) с поверхностью наклонного эллиптического цилиндра (рис. 12.8, д). Для этого использовалось задание плоскости общего положения α(k∩l) также двумя пересекающимися прямыми, одна из которых, как и в предыдущем случае, – это заданная прямая k(k»,k’), а пересекающаяся с ней в произвольной точке 1(1″,1′) вторая прямая линия – это прямая l(l»,l’), параллельная образующим цилиндра. Строился горизонтальный след этой плоскости и по точкам пересечения его с горизонтальным следом заданного цилиндра находились образующие, по которым вспомогательная плоскость общего положения α(k∩l) пересекает цилиндр. В местах пересечения с проекциями этих образующих проекций прямой общего положения k(k»,k’) находятся искомые проекции M»,M’ и N»,N’ точек пересечения заданной прямой с поверхностью цилиндра.

Касательные плоскости и нормаль к поверхности

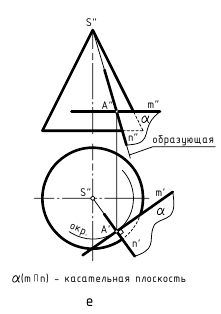
Плоскостью, касательной к поверхности в некоторой ее точке, называют плоскость, в которой можно провести две прямые линии, пересекающиеся в точке касания, касательные к двум пересекающимся в этой же точке линиям, принадлежащим поверхности.

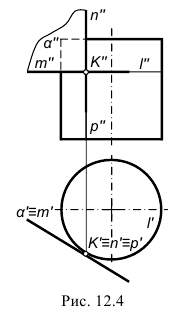
На чертеже касательную плоскость α(α»,α’) однозначно можно задать проекциями двух пересекающихся прямых m(m»,m’) и n(n»,n’). Эти линии строят касательно к проекциям двух пересекающихся в точке касания линий, принадлежащих поверхности. На рис. 12.4 линия m(m»,m’) является касательной к линии окружности l(l»,l’), проходящей через точку касания K(K»,K’) по поверхности цилиндра, а пересекающаяся с ней в этой точке линия n(n»,n’) сливается с линией р(р»,р’) – образующей цилиндра.

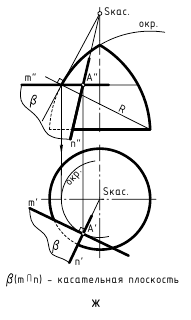
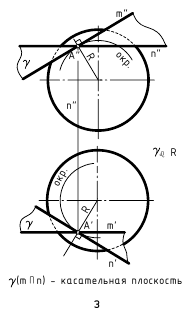
Аналогичные действия (рис. 12.8, е, ж, з) выполнены и при построении касательных плоскостей к поверхностям прямого кругового конуса, самопересекающегося тора и сферы, касающихся этих поверхностей в некоторой точке A(A»,A’). Пересекающиеся прямые m(m»,m’) и n(n»,n’), задающие касательные плоскости α(α»,α’) к ним, являются касательными к окружностям, построенным на этих поверхностях вращения и пересекающимся в точке касания A(A»,A’). Следует отметить одну особенность при построении прямой n(n»,n’), касательной к линии меридионального сечения поверхности самопересекающегося тора (рис. 12.8, ж). Для упрощения построений вначале строят касательную к этой линии, параллельной фронтальной плоскости проекций, определяют на оси вращения тора точку S, через которую проходят касательные ко всем точкам, расположенным на той же параллели поверхности, что и заданная точка касания A(A»,A’), а затем строят необходимую касательную n(n»,n’).

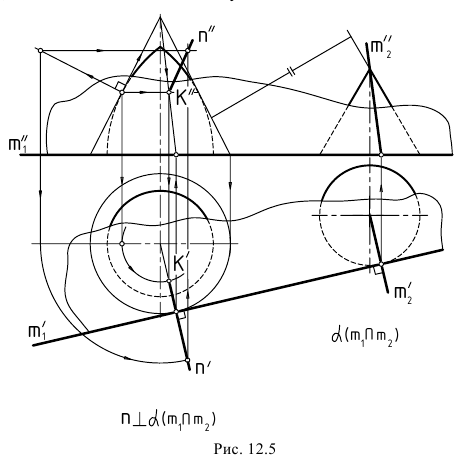
Эти построения использовались также для определения точки касания K(K»,K’) на поверхности самопересекающегося тора в задаче на рис. 12.5, где необходимо было задать общую касательную плоскость к поверхностям самопересекающегося тора и прямого кругового конуса. Ключом к решению задачи явилось заключение самопересекающегося тора в коническую поверхность с тем же углом наклона образующих, что и у заданного конуса (справа). Общая касательная плоскость задана пересекающимися прямыми, из которых m₁(m₁«,m₁‘), являющаяся горизонтальным следом плоскости, построена, как касательная к следам указанных конических поверхностей, а прямая m₂(m₂«,m₂‘), сливается с одной из образующих заданного конуса. Эта образующая является и геометрическим элементом касания построенной плоскости α(m₁∩m₂) с поверхностью заданного конуса. Поверхности самопересекающегося тора эта плоскость касается в точке K(K»,K’), которая найдена благодаря вышерассмотренным построениям и образующей второго конуса, охватывающего тор.

На рассматриваемом чертеже показано также построение нормали n(n»,n’), к поверхности самопересекающегося тора в точке K(K»,K’). Условием для построения нормали является ее перпендикулярность к плоскости, касательной к поверхности в той же точке. Вначале нормаль построена к очерковой образующей тора, затем на ней взята произвольная точка и выполнен ее поворот вокруг оси тора в положение, в котором она окажется расположенной в плоскости, перпендикулярной построенной касательной плоскости (направления указанных перемещений показаны стрелками).

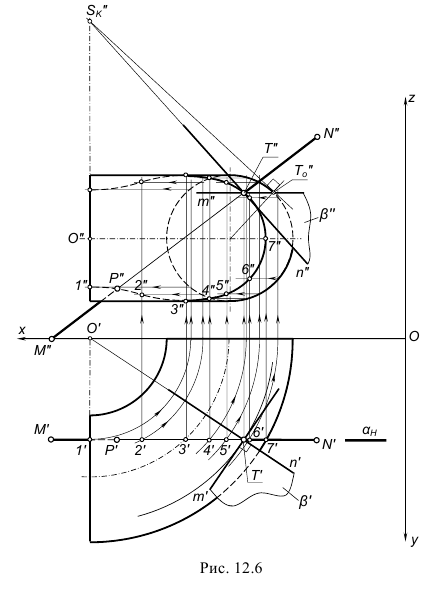
На рис. 12.6 показано построение точек пересечения P(P»,P’) и T(T»,T’) фронтальной прямой MN(M»N»,M’N’) с поверхностью ¼ кольцевого тора и построение касательной плоскости к этой поверхности в одной из построенных точек, например, T(T»,T’).

Точки P(P»,P’) и T(T»,T’) найдены благодаря заключению заданной прямой MN во фронтальную плоскость α(α_H) и построению проекций линии пересечения по точкам 1′, 2′, 3′, … , 7′, крайние из которых 1′ и 7′ взяты в местах пересечения горизонтального очерка плоскостью тора, а остальные – произвольно на горизонтальном следе α_H секущей плоскости. Для дальнейших построений использовались горизонтальные сечения поверхности тора плоскостями.

Для задания касательной плоскости β(m∩n) одна из задающих ее пересекающихся прямых m(m»,m’) построена как касательная к линии кольцевого сечения поверхности тора в точке T(T»,T’), а вторая – как касательная прямая n(n»,n’) к линии окружности осевого сечения поверхности тора. Для более точного построения второй прямой была найдена проекция S_K» точки на оси вращения тора, в которой сходятся все касательные прямые к поверхности тора во всех точках, находящихся на той же параллели, что и точка T(T»,T’).

Структуризация материала двенадцатой лекции в рассмотренном объеме схематически представлена на рис. 12.7 (лист 1). На последующем листе 2 компактно приведены иллюстрации к этой схеме для визуального закрепления изученного материала при повторении (рис. 12.8).

Пересечение линии с поверхностью:

Касательные плоскости и нормаль к поверхности

Касательная плоскость к кривой поверхности в некоторой точке – это плоскость, в которой лежат все касательные прямые ко всем кривым, которые можно провести на поверхности через ту же точку.

Нормалью к поверхности в данной точке называется прямая, перпендикулярная к касательной плоскости и проходящая через точку касания.

12.1. Пересечение прямой с поверхностью

12.2. Касательные плоскости

Рекомендую подробно изучить предметы:

Инженерная графика Начертательная геометрия Компас Автокад Черчение Проекционное черчение Аксонометрическое черчение Строительное черчение Техническое черчение Геометрическое черчение

Ещё лекции с примерами решения и объяснением:

• Проецирование прямой
• Взаимное положение плоскостей, прямой линии и плоскости
• Взаимное расположение точки, прямых и плоскостей
• Перпендикулярность геометрических объектов
• Прямая в пространстве и ее изображение на чертеже
• Многогранники
• Поверхности вращения
• Пересечение прямой линии с поверхностью

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

Источник