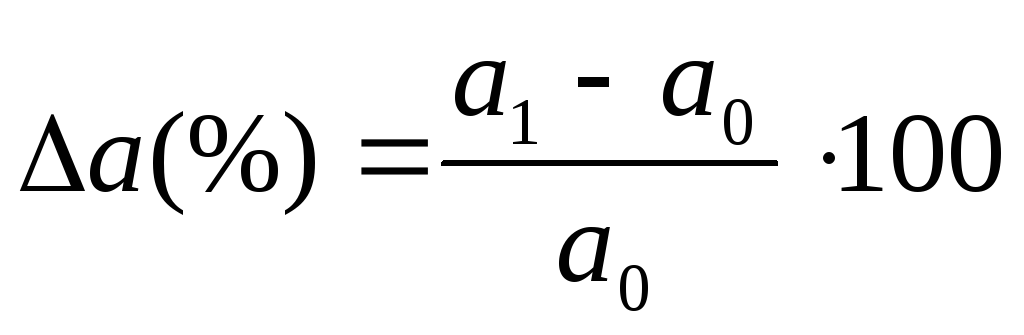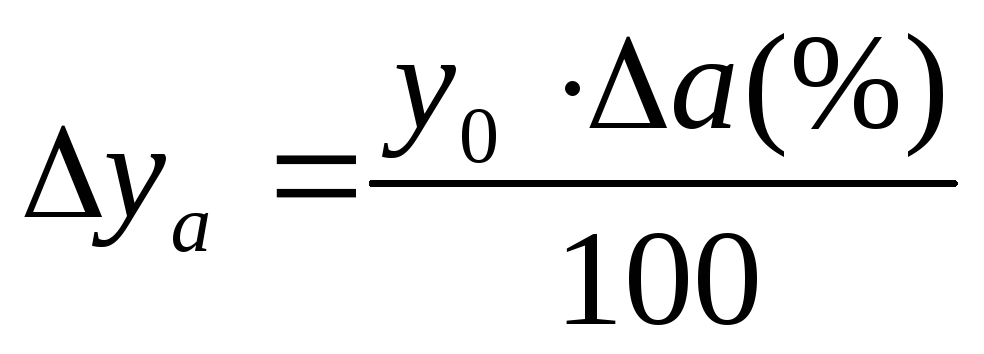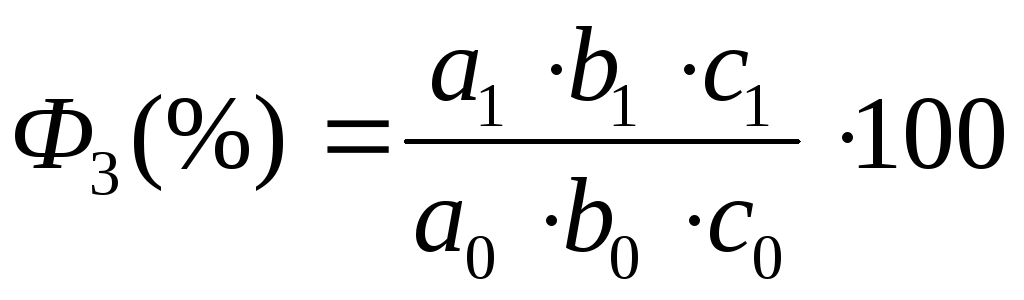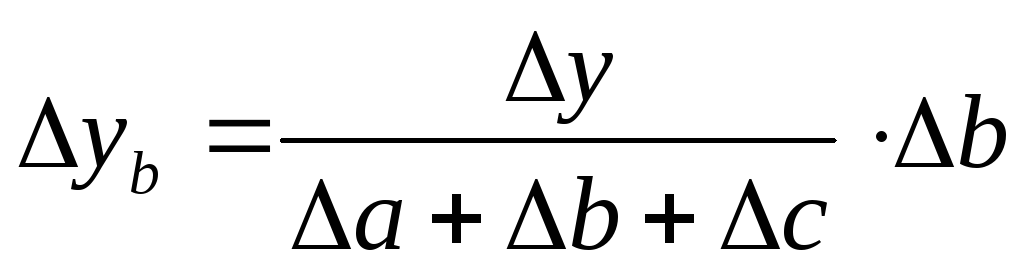Решение задач способ абсолютных разница

Способ абсолютных разниц детерминированного факторного анализа

Построив факторную модель детерминированного анализа, необходимо определить способ оценки влияния факторов. В детерминированном факторном анализе используют следующие основные способы:

• способ цепных подстановок;
• способ абсолютных разниц;
• способ относительных (процентных) разниц;
• интегральный метод и др.

Способ абсолютных разниц (абсолютных отклонений) является модификацией способа цепных подстановок. Он прост в расчетах, но менее универсален – с его помощью производят расчет влияния факторов только для мультипликативных моделей и моделей смешанного типа: Y=(a-b)c, Y=a(b-c).

Для мультипликативной модели расчет производится умножением абсолютного прироста исследуемого фактора на базисную величину факторов, находящихся справа от него, и на фактическую величину факторов, расположенных в модели слева от него.

В общем виде применение способа абсолютных разниц можно описать следующим образом:

y0 = a0 * b0 * c0;
Δya = Δa * b0 * c0;
Δyb = a1*Δb* c0;
Δyс = a1 * b1* Δс;
y1 = a1 * b1 * c1;
где a0, b0, c0 — базисные значения факторов, оказывающих влияние на обобщающий показатель у; a1 , b1, c1 — фактические значения факторов;
Δa=a1-a0, Δb=b1-b0, Δc=c1-c0, — абсолютные изменения (отклонение факта от базы или плана) факторов а, b, с соответственно.

Общее изменение Δу = у1 – у0 складывается из суммы изменений результирующего показателя за счет изменения каждого фактора:
Δy = Δya + Δyb + Δyc.

Пример применения способа абсолютных разниц

Порядок применения способа абсолютных разниц рассмотрим на следующем примере. Проанализировать влияние на валовый объем производства количества работников, количества отработанных дней одним работником и их выработки способом абсолютных разниц. Исходные данные представлены в таблице.

Показатель	Условное обозначение	Базисное значение (0)	Фактическое значение (1)	Абсолютное изменение (+,-)
Объем валовой продукции, тыс. руб.	ВП	2920	3380	+460
Среднесписочная численность персонала, чел.	ЧР	20	25	+5
Количество отработанных дней одним работником за год	Д	200	208	+8
Среднедневная выработка продукции одним работником, тыс. руб.	ДВ	0,73	0,65	-0,08

Решение. Зависимость объема производства продукции от данных факторов можно описать с помощью трехфакторной мультипликативной модели: ВП = ЧР * Д*ДВ.

Алгоритм расчета способом абсолютных разниц таков:

• ВП0 = ЧР0 * Д0*ДВ0 = 20*200*0,73 = 2920 тыс. руб.
• Влияние изменения количества работников на обобщающий показатель можно рассчитать по формуле:
  ΔВП(ЧР) = (ЧР1-ЧР2)*Д0*ДВ0 = (25-20)*200*0,73 = 730 тыс. руб.
• Влияние изменения количества отработанных дней одним работником на обобщающий показатель можно рассчитать по формуле:
  ΔВП(Д) = ЧР1*(Д1-Д0)*ДВ0 = 25*(208-200)*0,73 = 146 тыс. руб.
• Влияние изменения величины среднедневной выработки на обобщающий показатель можно рассчитать по формуле:
  ΔВП(ДВ) = ЧР1*Д1*(ДВ1-ДВ0) = 25*208*(0,65-0,73) = -416 тыс. руб.
• Суммарное влияние трех факторов определим по формуле:
  ΔВП = ΔВП(ЧР) + ΔВП(Д) + ΔВП(ДВ) = 730+146+(-416) = 460 тыс. руб. — значение совпадает с табличным и подтверждает правильность расчетов.

Вывод. Таким образом, на изменение объема производства продукции положительное влияние оказало увеличение на 5 человек численности работников, что вызвало увеличение объема производства на 730 тыс. руб. и увеличение количества отработанных дней на 8 каждым работником, что вызвало увеличение объема производства на 146 тыс. руб.
Отрицательное влияние оказало снижение среднедневной выработки на 80 руб., что вызвало снижение объема производства на 416 тыс. руб.
Суммарное влияние трех факторов привело к увеличению объема производства на 460 тыс. руб.

Источник

Способ абсолютных разниц

Вы будете перенаправлены на Автор24

Способ абсолютных разниц как разновидность метода элиминирования

Факторный анализ предполагает выявление факторов, влияющих на результирующий показатель, и определение степени их влияния. Одним из наиболее распространенных приемов определения степени влияния является элиминирование.

Элиминирование – это логический прием, позволяющий устранить влияние ряда факторов, выделив один фактор в качестве объекта изучения.

Сущность элиминирования состоит в следующем. Допустим, построена модель, в соответствии с которой результирующий показатель зависит от трех факторов. На практике все факторы могут меняться одновременно; может меняться два (а третий оставаться неизменным); может меняться лишь один (два остаются неизменными). Изменение факторов может обуславливать как рост показателя, так и его уменьшение. При этом изменение факторов может быть однонаправленным и разнонаправленным (например, численность персонала увеличилась – это должно способствовать увеличению выпуска, производительность труда снизилась – приводит к снижению выпуска, число рабочих дней увеличилось – способствует увеличению). При элиминировании последовательно рассматривается изменение только одного фактора (все остальные факторы предполагаются постоянными).

Метод абсолютных разниц (абсолютных отклонений), наряду с методом цепных подстановок, методом относительных отклонений и некоторыми другими, является способом осуществления элиминирования.

Методика способа абсолютных разниц

Способ абсолютных разниц применяется для определения степени влияния факторов на результирующий показатель в мультипликативных и мультипликативно-аддитивных моделях.

Мультипликативной называют модель, в которую факторы входят как члены произведения: $Y = a · b · c$.

Аддитивной называют модель, в которую факторы входят как члены алгебраической суммы (т.е. со знаком плюс или минус): $Y = a + b — c$.

Мультипликативно-аддитивная модель является смешанной моделью, объединяющей мультипликативную и аддитивную модели: $Y = a · (b + c)$.

Готовые работы на аналогичную тему

Таким образом, использование метода абсолютных разниц ограничено, он применим не для всех моделей. Но в силу распространенности моделей, для которых он предназначен, а также простоты самого метода, он широко применяется в анализе хозяйственной деятельности.

Сущность метода абсолютных разниц состоит в том, что величина влияния фактора определяется как произведение абсолютного прироста переменного фактора (анализируемого на данном шаге) на плановую (базовую) величину расположенных справа от него факторов и фактическую величину расположенных слева факторов.

Алгоритм расчета для мультипликативной модели, содержащей 4 фактора:

Определяем абсолютные отклонения каждого из факторов (отклонение фактического значения от планового):

Вычисляем влияние изменение факторов на результат:

Таким образом, на каждом шаге в произведении один из плановых показателей заменяется на абсолютное отклонение, а абсолютное отклонение, использованное на предыдущем шаге – на фактическое значение.

В смешанных моделях (мультипликативно-аддитивных) расчет производится несколько иначе. При вычислении влияния факторов, входящих в алгебраическую сумму, другие входящие в эту сумму факторы полностью исключаются из рассмотрения.

В целях контроля правильности вычислений необходимо проверить, чтобы сумма изменений, обусловленных каждым из анализируемых факторов, была равна общему изменению результирующего показателя. В выводах указывается, какое влияние (по направлению и объему) оказал каждый фактор.

Источник

3. Способ абсолютных разниц.

Метод абсолютных разниц используется в мультипликативных моделях и смешанных моделях типа y=a∙(b-c), y=(a-b)∙c.

При его использовании величина влияния факторов рассчитывается умножением абсолютного прироста исследуемого показателя на базовую (плановую) величину факторов, которые находятся справа от него в модели на фактическую величину факторов, находящихся слева от него в модели.

Рассмотрим трехфакторную мультипликативную модель.

4. Способ относительных и процентных разниц.

Способ относительных разниц применяется в мультипликативных и смешанных моделях типа y=(a-b)∙c.

Рассмотрим методику расчета на примере трехфакторной мультипликативной модели.

Cначала необходимо рассчитать относительное отклонение каждого фактора в процентах:

Находим влияние факторов.

Разновидностью метода относительных разниц является метод процентных разниц. Рассмотрим его на примере трехфакторной мультипликативной модели.

5. Способ пропорционального деления и долевого участия.

В ряде случаев, а именно в аддитивных моделях и смешанных моделях типа: y = a/(b + c + …) применяют метод пропорционального деления.

Рассмотрим трехфакторную аддитивную модель.

ПРИМЕР Рентабельность производства упала на 8%, при этом стоимость основных фондов выросла на 200 тысяч рублей, стоимость оборотных средств снизилась на 30 тысяч рублей. Способом пропорционального деления определить снижение рентабельности за счет каждого фактора.

∆R=-8%; ∆Ф=+200; ∆ОС=-30

ВЫВОД: за счет роста стоимости основных фондов на 200 тысяч рублей рентабельность упала на 9,4%. Снижение величины оборотных средств на 30 тысяч рублей привело к росту рентабельности на 1,4%.

Способ долевого участия является видоизменением данного метода. Сначала определяется доля прироста каждого фактора в общей сумме приростов и умножается на прирост результатного показателя.

6. Интегральный способ.

Интегральный метод не относится к методам элиминирования, поэтому порядок анализа факторов не имеет значения.

Этот метод применим в мультипликативных, кратных и смешанных моделях типа:

В интегральном методе пользуются определенными формулами.

Для двухфакторной мультипликативной модели y=a∙b

Для трехфакторной мультипликативной модели y=a∙b∙с

Для кратной модели типа:

7. Логарифмический способ.

Метод логарифмирования применяется для изменения влияния факторов только в мультипликативных моделях.

Порядок факторов в методе не важен. При использовании этого метода достигается еще более высокая точность, чем при использовании интегрального метода. В этом достоинство метода, а недостаток – в ограниченности применения.

Рассмотрим трехфакторную мультипликативную модель.

Прологарифмируем обе части равенства по любому основанию.

lg(y) = lg(a)+ lg(b) + lg(c)

Учитывая, что между индексами изменения показателей сохраняется та же зависимость, что и между самими показателями, заменим их абсолютные значения на индексы:

Умножим обе части равенства на :

∙∆у, ∙∆у, ∙∆у — частные приросты результативного показателя.

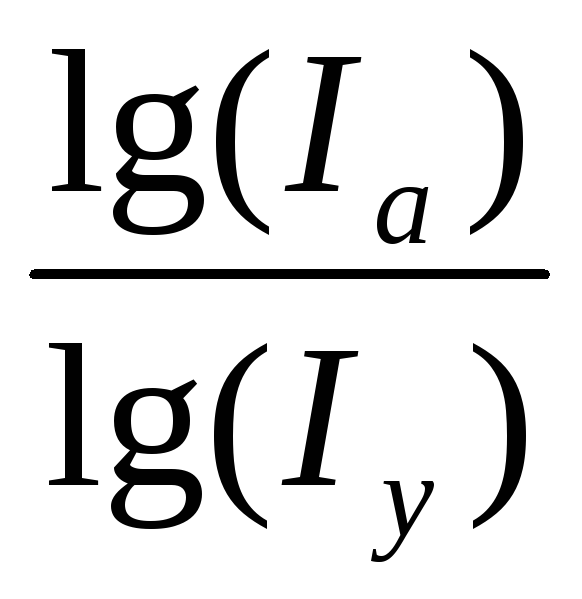
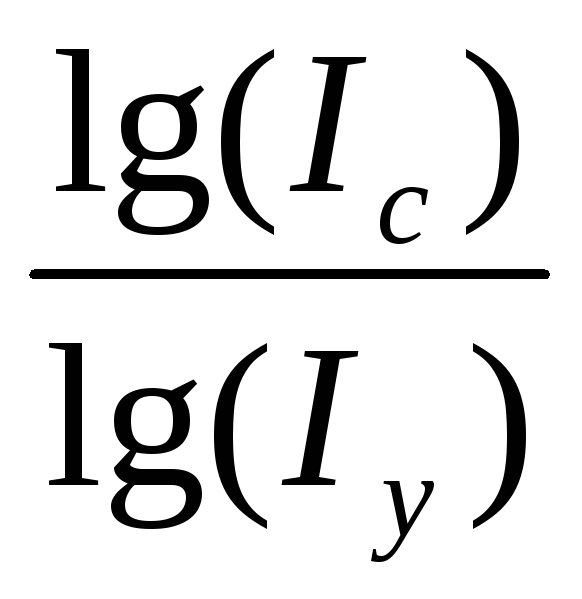
Источник