Решение задач линейного программирования графическим способом калькулятор

Решение задач линейного программирования

Решение происходит в три этапа:

1. Переход к КЗЛП. Любая ЗЛП вида ax ≤ b , ax ≥ b , ax = b ( F(X) → extr ) сводится к виду ax = b , F(X) → max ;
2. Переход к СЗЛП. КЗЛП вида ax = b сводится к виду ax ≤ b , F(X) → max ;
3. Решение симплексным методом;

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word

Переход от задачи минимизации целевой функции к задаче максимизации

Задача минимизации целевой функции F(X) легко может быть сведена к задаче максимизации функции F*(X) при тех же ограничениях путем введения функции: F*(X) = -F(X) . Обе задачи имеют одно и то же решение X*, и при этом min(F(X)) = -max(F*(X)) .
Проиллюстрируем этот факт графически:

F(x) → min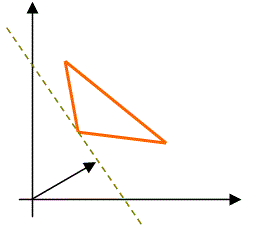

F(x) → max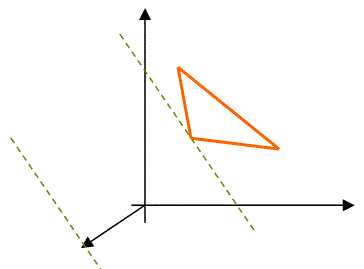

Для оптимизации функции цели используем следующие понятия и методы.
Опорный план – план с определёнными через свободные базисными переменными.
Базисный план – опорный план с нулевыми базисными переменными.
Оптимальный план – базисный план, удовлетворяющий оптимальной функции цели (ФЦ).

Ведущий (разрешающий) элемент – коэффициент свободной неизвестной, которая становится базисной, а сам коэффициент преобразуется в единицу.
Направляющая строка – строка ведущего элемента, в которой расположена с единичным коэффициентом базисная неизвестная, исключаемая при преобразовании (строка с минимальным предельным коэффициентом, см. далее).
Направляющий столбец – столбец ведущего элемента, свободная неизвестная которого переводится в базисную (столбец с максимальной выгодой, см. далее).

Переменные x₁, …, x_m, входящие с единичными коэффициентами только в одно уравнение системы, с нулевыми – в остальные, называются базисными или зависимыми. В канонической системе каждому уравнению соответствует ровно одна базисная переменная. Переход осуществляется с помощью метода Гаусса–Жордана. Основная идея этого метода состоит в сведении системы m уравнений с n неизвестными к каноническому виду при помощи элементарных операций над строками.
Остальные n-m переменных (x_m+1,…, x_n) называются небазисными или независимыми переменными.

Базисное решение называется допустимым базисным решением, если значения входящих в него базисных переменных x_j≥0, что эквивалентно условию неотрицательности b_j≥0.
Допустимое базисное решение является угловой точкой допустимого множества S задачи линейного программирования и называется иногда опорным планом.
Если среди неотрицательных чисел b_j есть равные нулю, то допустимое базисное решение называется вырожденным (вырожденной угловой точкой) и соответствующая задача линейного программирования называется вырожденной.

Источник

Сервис для решения задач по линейному программированию

и другие интересные типовые задачи English

Пример №2. Решение задачи линейного программирования графическим методом.
Функция достигает наименьшего значения в точке

при следующих ограничениях:

	x1	+	2 x2	≤	8
	x1	—	x2	≤	2
	x1	+	2 x2	≥	4
	x1	≥	1

x₁ ≥ 0 x₂ ≥ 0

Точки, координаты которых удовлетворяют одновременно всем неравенствам системы ограничений, называются областью допустимых решений.

Очевидно, для нахождения области допустимых решений данной задачи, необходимо последовательно рассмотреть каждое неравенство. (см. шаг 1 — шаг 4)

Последние два шага служат непосредственно для получения ответа. (см. шаг 5 — шаг 6)

Это стандартная схема решения. Если область допустимых решений представляет собой точку или пустое множество, то решение будет короче.

По условию задачи: x₁ ≥ 0 x₂ ≥ 0.

Если бы это было единственным условием, то область допустимых решений имела бы вид, как на рисунке (вся первая четверть).

Рассмотрим неравенство 1 системы ограничений.

Построим прямую: x₁ + 2 x₂ = 8

Найдены коородинаты двух точек (0, 4) и (8 ,0). Соединяем их и получаем необходимую прямую (1).

Нас интересуют точки расположенные выше или ниже построенной прямой (1) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≤ . Следовательно, нас интересуют точки расположенные ниже построенной прямой (1).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 2 системы ограничений.

Найдены коородинаты двух точек (0, -2) и (2 ,0). Соединяем их и получаем необходимую прямую (2).

Нас интересуют точки расположенные выше или ниже построенной прямой (2) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (2).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 3 системы ограничений.

Построим прямую: x₁ + 2 x₂ = 4

Найдены коородинаты двух точек (0, 2) и (4 ,0). Соединяем их и получаем необходимую прямую (3).

Нас интересуют точки расположенные выше или ниже построенной прямой (3) ?
Вернемся к исходному неравенству.

Преобразуем неравенство, оставив в левой части только x₂

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные выше построенной прямой (3).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Рассмотрим неравенство 4 системы ограничений.

Построим прямую: x₁ = 1

Данная прямая параллельна оси OX₂ и проходит через точку (1,0) (4)

Знак неравенства ≥ . Следовательно, нас интересуют точки расположенные правее построенной прямой (4).

Объединим данное условие с предыдущим рисунком. В итоге получим область допустимых решений, изображенную на рисунке.

Строим вектор C = (2, 2), координатами которого являются коэффициенты функции F.

Будем перемещать «красную» прямую, перпендикулярно вектору C , от левого нижнего угла к правому верхнему.

В точке, в которой «красная» прямая в первый раз пересечет область допустимых решений, функция F достигает своего наименьшего значения.

В точке, в которой «красная» прямая в последний раз пересечет область допустимых решений, функция F достигает своего наибольшего значения.

Функция F достигает наименьшего значения в точке A. (см. рисунок)

Найдем координаты точки A.
Точка A одновременно принадлежит прямым (3) и (4).

	x1	+	2 x2	=	4	=>	x1 = 1
	x1	=	1	x2 = 3/2

Вычислим значение функции F в точке A (1,3/2).

F (A) = 2 * 1 + 2 * 3/2 = 5

x₁ = 1

x₂ = 3/2

F _min = 5

Замечание: если возникли сомнения, что функция F достигает своего минимума в точке А, необходимо найти значение функции в интересующей точке и сравнить с F(A).

Источник

Симплексный метод решения ЗЛП

Назначение сервиса . Сервис предназначен для онлайн решения задач линейного программирования (ЗЛП) симплекс-методом в следующих формах записи:

• в виде симплексной таблицы (метод жордановых преобразований); базовой форме записи;
• модифицированным симплекс-методом; в столбцовой форме; в строчечной форме.

• Шаг №1
• Шаг №2
• Видеоинструкция
• Оформление Word
• Также решают

Задачи динамического программирования
Распределить 5 однородных партий товара между тремя рынками так, чтобы получить максимальный доход от их продажи. Доход от продажи на каждом рынке G(X) зависит от количества реализованных партий товара Х и представлен в таблице.

Объем товара Х (в партиях)	Доход G(X)
	1	2	3
0	0	0	0
1	28	30	32
2	41	42	45
3	50	55	48
4	62	64	60
5	76	76	72

Алгоритм симплекс-метода включает следующие этапы:

1. Составление первого опорного плана. Переход к канонической форме задачи линейного программирования путем введения неотрицательных дополнительных балансовых переменных.
2. Проверка плана на оптимальность. Если найдется хотя бы один коэффициент индексной строки меньше нуля, то план не оптимальный, и его необходимо улучшить.
3. Определение ведущих столбца и строки. Из отрицательных коэффициентов индексной строки выбирается наибольший по абсолютной величине. Затем элементы столбца свободных членов симплексной таблицы делит на элементы того же знака ведущего столбца.
4. Построение нового опорного плана. Переход к новому плану осуществляется в результате пересчета симплексной таблицы методом Жордана—Гаусса.

Базис	B	x1	x2	x3	x4	min
x3	20	5	2	1	0	20:5=4
x4	6	1	1	0	1	6:1=6
F(X1)	-8	-5	0	0	0

Если необходимо найти экстремум целевой функции, то речь идет о поиске минимального значения ( F(x) → min , см. пример решения минимизации функции) и максимального значения ( F(x) → max , см. пример решения максимизации функции)

Экстремальное решение достигается на границе области допустимых решений в одной из вершин угловых точек многоугольника, либо на отрезке между двумя соседними угловыми точками.

Основная теорема линейного программирования . Если целевая функция ЗЛП достигает экстремального значения в некоторой точке области допустимых решений, то она принимает это значение в угловой точке. Если целевая функция ЗЛП достигает экстремального значения более чем в одной угловой точке, то она принимает это же значение в любой из выпуклой линейной комбинации этих точек.

Суть симплекс-метода. Движение к точке оптимума осуществляется путем перехода от одной угловой точки к соседней, которая ближе и быстрее приближает к X_опт. Такую схему перебора точек, называемую симплекс-метод, предложил Р. Данцигом.
Угловые точки характеризуются m базисными переменными, поэтому переход от одной угловой точки к соседней возможно осуществить сменой в базисе только одной базисной переменной на переменную из небазиса.
Реализация симплекс-метода в силу различных особенностей и постановок задач ЛП имеет различные модификации.

Построение симплекс-таблиц продолжается до тех пор, пока не будет получено оптимальное решение.

Как с помощью симплекс-таблицы определить, что решение задачи линейного программирования является оптимальным?
Если последняя строка (значения целевой функции) не содержит отрицательных элементов, следовательно, найдет оптимальный план.

Замечание 1 . Если одна из базисных переменных равна нулю, то крайняя точка, соответствующая такому базисному решению — вырожденная. Вырожденность возникает, когда имеется неоднозначность в выборе направляющей строки. Можно вообще не заметить вырожденности задачи, если выбрать другую строку в качестве направляющей. В случае неоднозначности нужно выбирать строку с наименьшим индексом, чтобы избежать зацикливания.

Замечание 2 . Пусть в некоторой крайней точке все симплексные разности неотрицательные D_k³ 0 (k = 1..n+m),т.е. получено оптимальное решение и существует такой А_k – небазисный вектор, у которого D_k = 0. Тогда максимум достигается по крайней мере в двух точках, т.е. имеет место альтернативный оптимум. Если ввести в базис эту переменную x_k, значение целевой функции не изменится.

Замечание 3 . Решение двойственной задачи находится в последней симплексной таблице. Последние m компонент вектора симплексных разностей( в столбцах балансовых переменных) – оптимальное решение двойственной задачи. Значение целевых функций прямой и двойственной задачи в оптимальных точках совпадают.

Замечание 4 . При решении задачи минимизации в базис вводится вектор с наибольшей положительной симплексной разностью. Далее применяется тот же алгоритм, что и для задачи максимизации.

Если задано условие «Необходимо, чтобы сырье III вида было израсходовано полностью», то соответствующее условие представляет собой равенство.

Аналитическое введение в симплекс-метод

Итак, если мы решаем ЗЛП в канонической форме, то система ограничений — это обычная система линейных уравнений. При решении задач ЛП получаются системы линейных уравнений, имеющие, как правило, бесконечно много решений.

Например, пусть дана система

Здесь число уравнений равно 2, а неизвестных — 3, уравнений меньше. Выразим x₁ и x₂ через x₃ :

Это общее решение системы. если переменной x₃ придавать произвольные числовые значения, то будем находить частные решения системы. Например, x₃=1 → x₁=1 → x₂=6. Имеем (1, 6, 1) — частное решение. Пусть x₃=2 → x₁=-3, x₂= 1, (-3, 1, 2) — другое частное решение. Таких частных решений бесконечно много.

Переменные x₁ и x₂ называются базисными, а переменная x₃ — не базисная, свободная.

Совокупность переменных x₁ и x₂ образует базис: Б (x₁, x₂). Если x₃ = 0, то полученное частное решение (5, 11, 0) называется базисным решением, соответствующим базису Б (x₁, x₂).

Базисным называется решение, соответствующее нулевым значениям свободных переменных.
В качестве базисных можно было взять и другие переменные: (x₁, x₃) или (x₂, x₃).
Как переходить от одного базиса Б(x₁, x₂) к другому базису Б(x₁, x₃)?
Для этого надо переменную x₃ перевести в базисные, а x₂ — в небазисные т. е. в уравнениях надо x₃ выразить через x₂ и подставить в 1-е:

Базисное решение, соответствующее базису Б (x₁, x₃), таково: (-19/5; 0; 11/5).

Если теперь от базиса Б (x₁, x₃) нам захочется перейти к базису Б (x₂, x₃), то

Базисное решение, соответствующее базису Б (x₂, x₃): (0;19/4; 7/8).
Из трех найденных базисных решений решение, соответствующее базису Б (x₁, x₃) — отрицательное x₁ Пример . Решить задачу ЛП.

Эти ограничения могут рассматриваться как произошедшие из неравенств, а переменные x₃, x₅, x₄ — как дополнительные.
Запишем ограничения, выбрав базис из переменных Б< x₃, , x₄, x₅>:

Этому базису соответствует базисное неотрицательное решение
x₁ = 0, x₂ = 0, x₃ = 2, x₄ = 2, x₅ = 5 или (0, 0, 2, 2, 5).
Теперь нужно выразить F через небазисные переменные, в нашем случае это уже сделано: F= x₂ — x₁.
Проверим, достигла ли функция F своего минимального значения. Для этого базисного решения F= 0 — 0 = 0 — значение функции равно 0. Но его можно уменьшить, если x₁ будет возрастать, т. к. коэффициент в функции при x₁ отрицателен. Однако при увеличении x₁ значения переменных x₄, x₅ уменьшаются (смотрите второе и третье равенство системы ограничений). Переменная x₁ не может быть увеличена больше чем до 2, иначе x₄ станет отрицательной (ввиду равенства 2), и не больше, чем до 5, иначе x₅ — отрицателен. Итак, из анализа равенств следует, что переменную x₁ можно увеличить до 2, при этом значение функции уменьшится.
Перейдем к новому базису Б₂, введя переменную x₁ в базис вместо x₄.
Б₂<x₁, x₃, x₅>.
Выразим эти базисные переменные через небазисные. Для этого сначала выразим x₁ из второго уравнения и подставим в остальные, в том числе и в функцию.

Имеем:

F = -2 — x₂ + x₄.
Базисное решение, соответствующее базису Б₂<x₁, x₃, x₅>, имеет вид (2, 0, 6, 0, 3), и функция принимает значение F= -2 в этом базисе.
Значение функции можно и дальше уменьшать, увеличивая x₂. Однако, глядя на систему, x₂ можно увеличивать лишь до 1, т. к. иначе из последнего равенства x₅ = 3 — 3x₂ + x₄ следует, что при x₂ > 1 x₅ станет отрицательной. А у нас все переменные в ЗЛП предполагаются неотрицательными. Остальные уравнения системы не дают ограничений на x₂. Поэтому увеличим x₂ до 1, введя его в базис вместо x₅: Б₃<x₁, x₂, x₃>.
Выразим x₂ через x₅ и подставим во все уравнения:

Базисное решение, соответствующее базису Б₃<х₁, х₂, х₃>, выписывается (4, 1, 9, 0, 0), и функция принимает значение F= -3. Заметим, что значение F уменьшилось, т. е. улучшилось по сравнению с предыдущим базисом.
Посмотрев на вид целевой функции , заметим, что улучшить, т. е. уменьшить значение F нельзя и только при x₄ = 0, x₅ = 0 значение F= -3. как только x₄, x₅ станут положительными, значение F только увеличится, т. к. коэффициенты при x₄, x₅ положительны. Значит, функция F достигла своего оптимального значения F* = -3. Итак, наименьшее значение F, равное -3, достигается при x₁* = 4, x₂* = 1, x₃* = 9, x₄* = 0, x₅* = 0.

На этом примере очень наглядно продемонстрирована идея метода: постепенно переходя от базиса к базису, при этом всегда обращая внимание на значения целевой функции, которые должны улучшиться, мы приходим к такому базису, в котором значение целевой функции улучшить нельзя, оно оптимально. Заметим, что базисов конечное число, поэтому количество шагов, совершаемых нами до того нужного базиса, конечно.

Источник