Решение задач кинематики задача встреча аналитический способ решения

Решение задач кинематики .Задача «встреча» аналитический способ 7 кл

Тема урока: решение задач кинематики .Задача «встреча» аналитический способ

Тип урока: изучение нового материала.

Цели урока: 1. Должен знать учащийся : способы описание прямолинейного движения : табличный, графический

2. Должен уметь учащийся : применять закон прямолинейного равномерного движения к решению задач, Определять координаты тела , скорость тела

Познавательные : Добывать новые знания: находить ответы на вопросы, используя учебник, свой жизненный опыт и информацию, полученную на уроке.

Регулятивные: Проговаривать последовательность действий на уроке. Учиться высказывать своё предположение (версию) на основе работы с иллюстрацией учебника.

Коммуникативные: Слушать и понимать речь других.

Оборудование: рабочая тетрадь , учебник

Приемы и методы

План изложения нового материала.

Беседа. Фронтальный опрос

Приведите примеры встречи двух тел. что означает в кинематике, что два тела встретились ?

Перечислите шаги решения задачи « встреча» графическим способом

Отвечают на вопросы

2.Изучение нового материала.

Работа с учебником, у доски, в тетради

Решим задачу о нахождении места и времени встречи пешехода и велосипедиста другим способом- аналитическим.

Вспомните первые три шага решения этой задачи графическим способом:

Шаг 1.: Введем систему отсчета: начало отсчета-дерево .Направление координатной оси- вдоль дороги в направлении движения пешехода.

Включить часы в момент начала движения

Шаг2: начальные координаты

Велосипедиста х _во = 20м

Шаг 3 : используя введенную систему отсчета определили значение скоростей движения

Велосипедиста v _в = -3м/с

Работа с учебником, рабочей тетрадью

Но следующие шаги будут отличаться от шагов графического способа

Шаг4: запишем законы движения тел учитывая известные данные

Шаг5: условие встречи: встреча двух тел означает, что положения тел в пространстве совпадают в некоторый момент времени t = t _вс

Шаг6: з апишите полученные выражения

Шаг7 : решение уравнений

РТ п 11 задача1

закон движения пешехода

Закон движения велосипед.

Х _п = 0+1 t = 0+1 5= 5(м)

Х _в = 20-3 t = 20-3 5= 5(м)

РТ п 11 задача 3

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 798 человек из 78 регионов

Курс профессиональной переподготовки

Физика: теория и методика преподавания в образовательной организации

• Сейчас обучается 357 человек из 66 регионов

Курс профессиональной переподготовки

Методическая работа в онлайн-образовании

• Сейчас обучается 27 человек из 16 регионов

Ищем педагогов в команду «Инфоурок»

Номер материала: ДБ-475570

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Учителям предлагают 1,5 миллиона рублей за переезд в Златоуст

Время чтения: 1 минута

Минпросвещения работает над единым подходом к профилактике девиантного поведения детей

Время чтения: 1 минута

В 16 регионах ввели обязательную вакцинацию для студентов старше 18 лет

Время чтения: 1 минута

На новом «Уроке цифры» школьникам расскажут о разработке игр

Время чтения: 1 минута

Педагогов и учеников предлагают тренировать на случай нападения

Время чтения: 1 минута

Российские школьники установили рекорд на олимпиаде по астрономии

Время чтения: 2 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Движение тел относительно друг друга. Задача «встреча»

Рассмотрим, как будет выглядеть решение уже знакомой нам задачи «встреча» в системе отсчета, связанной с одним из движущихся тел.

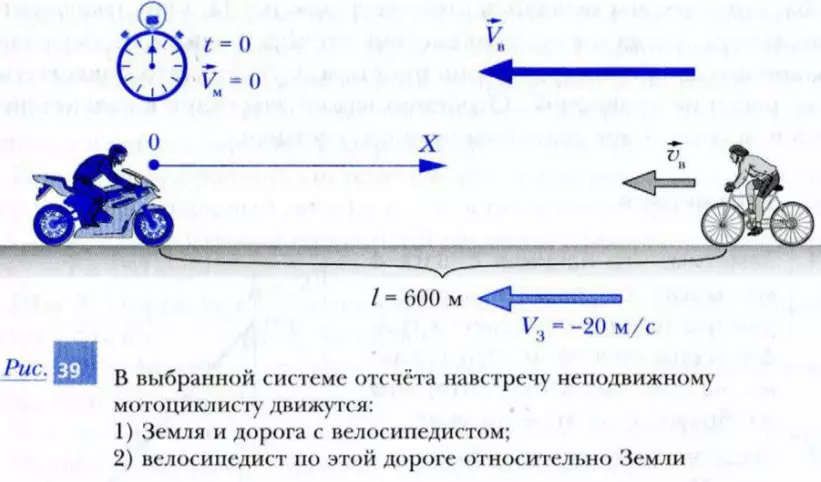
Пусть по прямолинейной дороге навстречу друг другу едут мотоциклист и велосипедист, как показано на рис. 38. При этом относительно Земли модуль скорости мотоциклиста |v_м| = 20 м/с, а модуль скорости велосипедиста – |v_в| = 10 м/с. Определим, через какое время произойдет их встреча, если в момент начала наблюдения расстояние между ними l = 600 м.

Шаг 1. Пусть начало отсчета совпадает с мотоциклистом. Ось X направим вдоль дороги от мотоциклиста в сторону велосипедиста, как показано на рис. 39. В качестве единицы длины выберем 1 м. Часы (секундомер) включим в момент начала наблюдения.

Шаг 2 . Найдем начальную координату велосипедиста x_в0 в момент времени t = 0. Видно, что в выбранной системе отсчета x_в0 = 600 м, так как расстояние от начала отсчета (мотоциклиста) до велосипедиста l = 600 м.

Шаг 3. В выбранной системе отсчета мотоциклист неподвижен (так как он является началом отсчета и его координата все время равна x_м = 0). Определим значение скорости велосипедиста. В выбранной системе отсчета Земля вместе с дорогой движутся в отрицательном направлении оси X со скоростью, имеющей значение V_з = -|v_м| = -20 м/с. Велосипедист по условию задачи движется относительно Земли также в отрицательном направлении оси X (навстречу мотоциклисту) со скоростью, имеющей значение v_в = -10 м/с. Значит, относительно выбранной системы отсчета (мотоциклиста) велосипедист будет двигаться со скоростью, значение которой равно V_в = V_з + v_в = (-20) + (-10) = -30 м/с. Напомним, что здесь, как и в предыдущем параграфе, мы обозначаем буквами v значения скоростей относительно Земли, а значения скоростей тел в выбранной системе отсчета – большими буквами V.

Шаг 4 . Запишет законы движения мотоциклиста и велосипедиста:

Шаг 5 . Представим в виде уравнения условие задачи, т. е. условие встречи мотоциклиста и велосипедиста. Как вы помните, это условие означает равенство координат движущихся навстречу друг другу тел. Поэтому

Шаг 6. Объединим полученные уравнения, присвоив каждому из них номер и название:

x_м = 0 (1) (закон движения мотоциклиста)
x_в = 600 — 30 · t, (2) (закон движения велосипедиста)
x_в = x_м. (3) (условие встречи)

Шаг 7 . Решим полученные уравнения, подставив в условие встречи (3) координаты x_м и x_в из уравнений (1) и (2):

0 = 600 — 30 · t,
t_встр = t = 600/30 = 20 (с).

Таким образом, встреча произойдет через 20 с.

Обратим внимание на существенное отличие данного способа решения от способа, которым мы решали задачу «встреча» раньше. Оно заключается в том, что теперь, когда мы связали систему отсчета с одним из движущихся тел, закон его движения стал очень простым: x_м(t) = 0. Это существенно упростило решение уравнений. Особенно важно это будет в дальнейшем, когда тела в задачах будут двигаться намного сложнее.

Упражнения

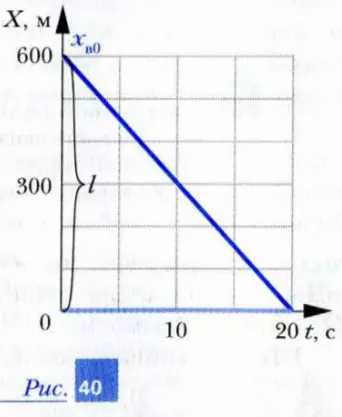
1. Заметим, что начиная с шага 4 мы могли бы решить рассмотренную только что задачу и графическим способом. Это сделано на рис. 40. Объясните, что изображено на этом рисунке.

2. Решите задачу, изображенную на рис. 38, в системе отсчета, связанной с велосипедистом. (Особое внимание уделите вопросам: куда направить координатную ось? Куда и с какой скоростью в этой системе отсчета будут двигаться Земля и мотоциклист?)

3. Выполните упражнение 2 графическим способом начиная с шага 4.

4. Решите в общем виде задачу, условие которой изображено на рис. 38, в системе отсчета, связанной с мотоциклистом. Проведите анализ полученного решения.

Источник

Задача «встреча». Аналитический способ решения

Теперь решим задачу из предыдущего параграфа другим способом – аналитическим. Посмотрим на рис. 20 и вспомним, что было сделано за первые три шага решения этой задачи.

Шаг 1 . Мы ввели систему отсчета: 1) выбрали началом отсчета дерево, от которого начинал свое движение пешеход; 2) направили координатную ось вдоль дороги в направлении движения пешехода; 3) включили часы (секундомер) в момент начала движения тел.

Шаг 2 . Были определены начальные координаты пешехода (x_п0 = 0) и велосипедиста (x_в0= 20 м).

Шаг 3 . Используя введенную систему отсчета, мы определили значения скоростей движения пешехода (v_п = 1 м/с) и велосипедиста (v_в = -3 м/с).

Таким образом, первые три шага решения задачи не зависят от того, каким способом (графическим или аналитическим) мы собираемся ее решать. Но уже следующий шаг будет отличаться от того, что мы делали при графическом способе решения.

Шаг 4 (аналитический). Запишем в аналитическом виде законы движения тел, учитывая известные данные. Поскольку в задаче движутся два тела (пешеход и велосипедист), то мы получаем два закона движения:

x_п = 0 + 1 · t, x_в = 20 — 3 · t.

Шаг 5 (аналитический) . Представим в виде уравнения условие задачи – встречу велосипедиста и пешехода. Встреча двух тел означает, что положения тел в пространстве совпадут в некоторый момент времени t = t_встр, т. е. в этот момент времени совпадут их координаты. Поэтому условие встречи будет иметь вид:

Шаг 6 (аналитический) . Запишем вместе полученные в шагах 4 и 5 выражения, присвоив каждому из них свои номер и название.
x_п = 0 + 1 · t, (1) (закон движения пешехода)
x_в = 20 — 3 · t, (2) (закон движения велосипедиста)
x_п = x_в. (3) (условие встречи пешехода и велосипедиста)

Шаг 7 (аналитический). Решение уравнений.

Для того чтобы найти значение времени t в интересующий нас момент встречи, воспользуемся условием встречи пешехода и велосипедиста – уравнением (3). Оно предполагает равенство координат двух тел. Подставим в него выражения для x_п и x_в из уравнений (1) и (2):

0 + 1 · t = 20 — 3 · t

Приведем подобные слагаемые и решим уравнение:

(1+3) · t = 20, t = 20/4 = 5 (с).

Таким образом, мы установили, что встреча пешехода и велосипедиста состоится через 5 с после начала движения.

Теперь определим координату точки, в которой состоится встреча. Для этого подставим полученное значение момента встречи t_встр = 5 с в закон движения пешехода – уравнение (1):

x_п = 0 + 1 · t_встр = 0 + 1 · 5 = 5 (м).

Это означает, что в момент встречи координата пешехода будет равна x_п = 5. Следовательно, встреча произойдет в 5 м от начала отсчета – дерева, от которого начал движение пешеход.

Ясно, что координату места встречи можно было определить, подставив время t_встр = 5 с и в закон движения велосипедиста – уравнение (2):

x_в = 20 — 3 · t_встр = 20 — 3 · 5 = 5 (м).

Естественно, мы получили то же самое значение хвстр, так как координаты пешехода и велосипедиста в момент встречи совпадают.

Итоги
При аналитическом способе решения задачи «встреча» момент встречи и координата места встречи определяются из равенства координат в законах движения тел, записанных в аналитическом виде.

1. Определите аналитическим способом время и место встречи пешехода и велосипедиста (начните с шага 3) в выбранной нами ранее системе отсчета, связанной с деревом, если:
а) значение скорости пешехода осталось прежним v_п = 1 м/с, а велосипедист едет ему навстречу со скоростью |v_в| = 4 м/с;
б) значение скорости пешехода v_п = 3 м/с, а велосипедист едет со скоростью, значение которой v_в = -7 м/с.

2. Выполните предыдущее упражнение, решая задачу графическим способом.

3. Определите аналитическим способом время и координату встречи пешехода и велосипедиста, которые движутся навстречу друг другу со скоростями |v_п| = 2 м/с и |v_в| = 8 м/с, если начальное расстояние между ними l = 160 м и они начинают движение одновременно. (Начните решение с шага 1.)

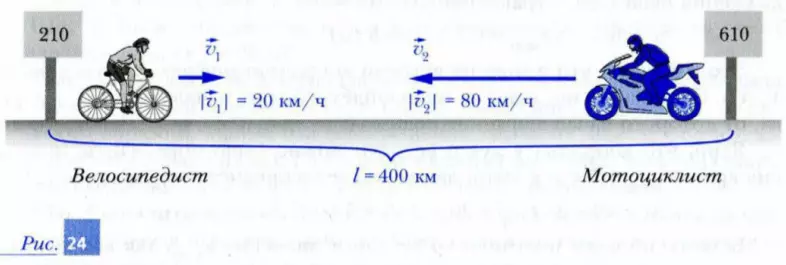
4. Сформулируйте условие и решите задачу о встрече велосипедиста и мотоциклиста, изображенных в момент времени t = 0 на рис. 24.

Источник