Решение задач кинематики аналитическим способом

Задача «встреча». Аналитический способ решения

Теперь решим задачу из предыдущего параграфа другим способом – аналитическим. Посмотрим на рис. 20 и вспомним, что было сделано за первые три шага решения этой задачи.

Шаг 1 . Мы ввели систему отсчета: 1) выбрали началом отсчета дерево, от которого начинал свое движение пешеход; 2) направили координатную ось вдоль дороги в направлении движения пешехода; 3) включили часы (секундомер) в момент начала движения тел.

Шаг 2 . Были определены начальные координаты пешехода (x_п0 = 0) и велосипедиста (x_в0= 20 м).

Шаг 3 . Используя введенную систему отсчета, мы определили значения скоростей движения пешехода (v_п = 1 м/с) и велосипедиста (v_в = -3 м/с).

Таким образом, первые три шага решения задачи не зависят от того, каким способом (графическим или аналитическим) мы собираемся ее решать. Но уже следующий шаг будет отличаться от того, что мы делали при графическом способе решения.

Шаг 4 (аналитический). Запишем в аналитическом виде законы движения тел, учитывая известные данные. Поскольку в задаче движутся два тела (пешеход и велосипедист), то мы получаем два закона движения:

x_п = 0 + 1 · t, x_в = 20 — 3 · t.

Шаг 5 (аналитический) . Представим в виде уравнения условие задачи – встречу велосипедиста и пешехода. Встреча двух тел означает, что положения тел в пространстве совпадут в некоторый момент времени t = t_встр, т. е. в этот момент времени совпадут их координаты. Поэтому условие встречи будет иметь вид:

Шаг 6 (аналитический) . Запишем вместе полученные в шагах 4 и 5 выражения, присвоив каждому из них свои номер и название.
x_п = 0 + 1 · t, (1) (закон движения пешехода)
x_в = 20 — 3 · t, (2) (закон движения велосипедиста)
x_п = x_в. (3) (условие встречи пешехода и велосипедиста)

Шаг 7 (аналитический). Решение уравнений.

Для того чтобы найти значение времени t в интересующий нас момент встречи, воспользуемся условием встречи пешехода и велосипедиста – уравнением (3). Оно предполагает равенство координат двух тел. Подставим в него выражения для x_п и x_в из уравнений (1) и (2):

0 + 1 · t = 20 — 3 · t

Приведем подобные слагаемые и решим уравнение:

(1+3) · t = 20, t = 20/4 = 5 (с).

Таким образом, мы установили, что встреча пешехода и велосипедиста состоится через 5 с после начала движения.

Теперь определим координату точки, в которой состоится встреча. Для этого подставим полученное значение момента встречи t_встр = 5 с в закон движения пешехода – уравнение (1):

x_п = 0 + 1 · t_встр = 0 + 1 · 5 = 5 (м).

Это означает, что в момент встречи координата пешехода будет равна x_п = 5. Следовательно, встреча произойдет в 5 м от начала отсчета – дерева, от которого начал движение пешеход.

Ясно, что координату места встречи можно было определить, подставив время t_встр = 5 с и в закон движения велосипедиста – уравнение (2):

x_в = 20 — 3 · t_встр = 20 — 3 · 5 = 5 (м).

Естественно, мы получили то же самое значение хвстр, так как координаты пешехода и велосипедиста в момент встречи совпадают.

Итоги
При аналитическом способе решения задачи «встреча» момент встречи и координата места встречи определяются из равенства координат в законах движения тел, записанных в аналитическом виде.

1. Определите аналитическим способом время и место встречи пешехода и велосипедиста (начните с шага 3) в выбранной нами ранее системе отсчета, связанной с деревом, если:
а) значение скорости пешехода осталось прежним v_п = 1 м/с, а велосипедист едет ему навстречу со скоростью |v_в| = 4 м/с;
б) значение скорости пешехода v_п = 3 м/с, а велосипедист едет со скоростью, значение которой v_в = -7 м/с.

2. Выполните предыдущее упражнение, решая задачу графическим способом.

3. Определите аналитическим способом время и координату встречи пешехода и велосипедиста, которые движутся навстречу друг другу со скоростями |v_п| = 2 м/с и |v_в| = 8 м/с, если начальное расстояние между ними l = 160 м и они начинают движение одновременно. (Начните решение с шага 1.)

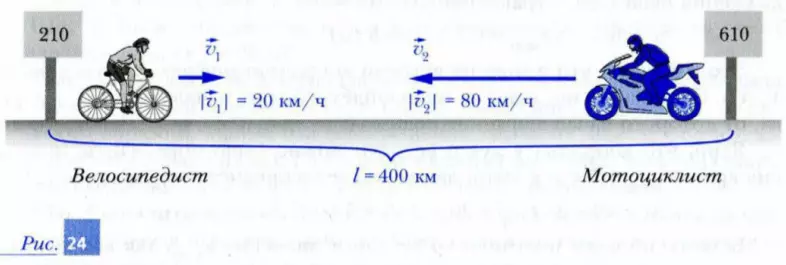
4. Сформулируйте условие и решите задачу о встрече велосипедиста и мотоциклиста, изображенных в момент времени t = 0 на рис. 24.

Источник

Обзор методов решения обратной задачи кинематики

4. Обзор методов решения обратной задачи кинематики

Обратная задача кинематики, как и прямая задача о положении, является одной из основных задач кинематического анализа и синтеза манипуляторов. Управление манипуляционными роботами, как правило, осуществляется в пространстве обобщенных координат, а координаты объектов манипулирования задаются в некоторой базовой системе. Таким образом, для управления положением и ориентацией робота возникает необходимость получения решения обратной задачи.

Обратная задача кинематики о положении состоит в определении обобщенных координат манипулятора:

,

по заданным в опорной системе координатам выходного звена — схвата робота:

где n — число степеней свободы.

Для решения обратной задачи необходимым условием является

,

означающее, что в этом случае можно составить n независимых уравнений, число неизвестных в котором также равно n.

Как правило, обратная задача оказывается более сложной по сравнению с прямой. Это объясняется следующим.

При решении обратной задачи кинематики может возникнуть кинематическая неопределенность, когда для одного и того же положения схвата может существовать две или более конфигураций манипулятора, т. е. для одного набора может существовать несколько наборов и в результате задача решается неоднозначно.

На практике для выбора однозначного решения обратной задачи кинематики обычно используют дополнительное условие, например, наличие ограничений в кинематических парах, наличие препятствий в зоне обслуживания и т. д.

Условие (3) не является достаточным, поэтому существуют варианты, когда при его соблюдении решение обратной задачи отсутствует. Для того, чтобы в этом случае задача имела решение, следует уменьшить m на единицу.

Таким образом, в случае, если n m, то решение обратной задачи существует, однако обратная задача в этом случае решается неоднозначно. Говорят, что манипулятор имеет избыточные степени подвижности. На практике это означает, что избыточные степени повышают функциональные возможности манипулятора.

Еще одна сложность, связанная с решением обратной задачи кинематики, заключается в том, что аналитические соотношения содержат, как правило, обратные тригонометрические функции, которые являются неопределенными при некоторых значениях углов, что вносит дополнительную неопределенность в решение обратной задачи.

Существуют различные методы получения решения обратной задачи, но, в целом, все методы решения обратной задачи кинематики можно разделить на аналитические и численные. Ниже рассмотрены ограничения, достоинства и недостатки каждого из методов.

4.1. Аналитические методы

К достоинствам аналитического метода решения обратной задачи кинематики относят получение произвольной точности решения. Однако, нахождение точного решения в виде аналитических зависимостей для обобщенных координат от конструктивных параметров и заданного вектора положения манипулятора представляется возможным не для всех манипуляторов. Аналитическое решение, таким образом, существует только для роботов с определенной конструкцией. Например, оси части смежных сочленений должны пересекаться в одной точке или должны быть параллельны либо перпендикулярны между собой.

Нахождение обобщенных координат в явном виде достаточно сложная задача, поскольку уравнения являются нелинейными. Для упрощения задачи существует ряд методов, предназначенных для более простого получения аналитических выражений. Метод обратных преобразований позволяет решать обратную задачу кинематики простых манипуляторов. Суть метода заключается в определении углов поворотов звеньев из уравнений для отдельных элементов имеющегося матричного уравнения. Например, для углов Эйлера (задающих ориентацию схвата) (3) получим систему уравнений:

,

Откуда можно определить:

Функция arccos считается неустойчивой вследствие того, что точность вычисления зависит от этого значения, кроме того, в точках, где принимает близкие к нулю значения, т. е. или , значения в (6) либо не определены, либо дают низкую точность вычислений. Обобщенные координаты чаще выражаются через функцию arctg с учетом принадлежности аргумент соответствующему квадранту.

Элементы матрицы в левой части матричного уравнения (4) заданы, а элементы матриц, стоящих в правой части этого уравнения, неизвестны и зависят от . В методе предлагается последовательно умножать слева обе части уравнения на матрицы обратных преобразований и определять искомые углы из полученных таким образом матричных уравнений. Смысл таких преобразований состоит в переносе сначала одной из неизвестных величин из правой в левую часть уравнения, ее нахождении и переносе в левую часть следующей неизвестной и повторении данной процедуры до нахождения всех переменных.

Хотя метод обратных преобразований дает общий подход к решению, из него не следует, каким образом выбирать из нескольких существующих решений одно, соответствующее требуемой конфигурации манипулятора.

Для нахождения решения обратной задачи кинематики по заданной матрице манипулятора используется геометрический подход, дающий также способ выбора единственного решения для конкретной конфигурации манипулятора. Данный способ, рассмотренный на примере шестизвенного манипулятора типа Пума, подробно описан в [1].

Кроме того, в [4] предложено решение обратной задачи кинематики для того же манипулятора, полученное в дуальных параметрах Родрига – Гамильтона, а именно с помощью бикватернионных матриц.

Как уже отмечалось, к недостаткам аналитического решения относятся сложность получения обобщенных координат в явном виде и неопределенность, связанная с кинематической неоднозначностью и используемыми тригонометрическими функциями. Однако, основным недостатком все же является невозможность получения решения для произвольных конструкций манипуляторов. Вернее, манипуляторы уже проектируются с учетом того, что описание кинематики будет возможно с помощью аналитических выражений.

В случае, если решение обратной задачи в виде аналитических выражений невозможно, используются численные методы.

4.2. Численные методы

Общая постановка задачи, например, для трехзвенного манипулятора с тремя вращательными парами формулируется следующим образом. Известны положения схвата в пространстве: начальное Pн, действительное Pд (определенное на i-м шаге корректировки) и конечное (желаемое) Pж положения, задаваемые декартовыми координатами. Необходимо определить такие значения обобщенных координат qi, , которые обеспечивали бы положение центра схвата в точке Pж (желаемое положение).

Поставленная таким образом задача является задачей минимизации функции трех переменных, и целевая функция будет иметь вид:

,

где — радиус–векторы действительного и желаемого положения центра схвата.

В случае многозвенного манипулятора, когда число степей свободы больше трех, необходимо знать еще и ориентацию манипулятора в пространстве. Таким образом, для определения ориентации манипулятора с числом степеней свободы n f(q1) > >f(q2) >…. В этом случае метод обеспечивает сходимость, и можно надеяться, что минимум функции будет найден.

Важной характеристикой методов является их скорость сходимости. Однако оценка сходимости того или иного метода обычно базируется на некоторых теоретических предпосылках, связанных с особенностями целевой функции (например, функция дважды непрерывно дифференцируема или сильно выпукла), а также зависит от выбора начальной точки поиска. Теоретические предпосылки относительно реальных целевых функций могут не удовлетворяться, поэтому скорость сходимости в этих случаях можно рассматривать как сравнительную оценку метода.

Численные методы позволяют построить последовательность шагов от начальной точки q0 через некоторые промежуточные точки qk к локальному экстремуму (минимуму) q*. Как отмечалось выше, выбор исходной точки поиска q0 во многом определяет успех решения всей задачи. Очевидно, что q0 должна принадлежать области определения целевой функции и, чем ближе к экстремуму выбрана q0, тем быстрее и с большой вероятностью экстремум будет найден. Сущность метода оптимизации определяется этапами 2 и 3 алгоритма, на которых выбирается направление дальнейшего поиска и вычисляются координаты очередной точки qk+1 на траектории поиска. Далее в точке qk+1 вычисляются значения целевой функции f(qk+1), т. е. определяется информация, позволяющая судить о достигнутом успехе. В зависимости от выполнения назначенных условий прекращения поиска поиск будет продолжен или прекратится.

Численный метод позволяет решить обратную задачу кинематики для тех конструкций манипуляторов, для которых получение точного решения в аналитических выражениях не представляется возможным либо достаточно затруднительно. Это является основным достоинством при использовании численного метода применительно к поставленной задаче.

Кроме того, численные методы решения обратной задачи позволяют достичь требуемой точности решения. Однако время сходимости того или иного метода заранее неизвестно и во многом зависит от начального приближения. В результате, чувствительность к количеству переменных целевой функции, виду гиперповерхности, а также различная скорость сходимости и потери на поиск требуют значительных вычислительных мощностей, что затрудняет их использование в реальном времени.

Источник