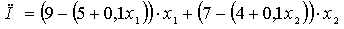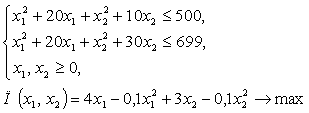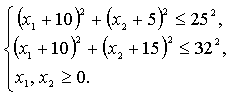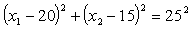Электронная библиотека
Графо-аналитический метод применим только для двух- или трехмерной целевой функции. Решение задачи линейного программирования данным методом осуществляется в два этапа:
· на первом этапе строим область допустимых решений, соответствующую системе ограничений. Для этого приравниваем их левые и правые части, и определяем направления расположения допустимых значений искомых переменных в соответствии со знаками неравенств;
· на втором этапе производим окончательное определение оптимальных значений переменных. Для этого строим произвольную прямую, соответствующую целевой функции. После этого необходимо построить прямую линию, параллельную данной прямлй, чтобы она коснулась границы области допустимых решений.
Координаты точки касания этой прямой с границей области допустимых решений будут оптимальными значениями переменных. Следует также отметить, что максимальное значение целевой функции будет достигаться при выходе этой прямой из области допустимых решений при движении прямой слева направо, а минимальное значение соответсвтенно при входе.
Пример
Дана целевая функция
с системой ограничений
Найти оптимальные значения и .
Строим область допустимых решений (ОДР).
Для формирования ОДР необходимо в системе координат построить линии, соответствующие ограничениям, приравнивая их левые и правые части, и определить направления расположения допустимых значений искомых переменных в соответствии со знаками неравенств (рис. 7.1).
Рис. 7.1 Графическая иллюстрация решения задачи линейного
Вычисления для построения первых двух ограничений:
Источник
Графоаналитический метод решения задач с нелинейной системой ограничений и целевой функцией
Исходя из уровня знаний, подготовки, и следуя наиболее понятному для студенчества наглядному способу решения задач, было решено практиковать на занятиях по дисциплинам: исследование операций и экономико-математические методы решения задач, графоаналитические методы решения задач нелинейного программирования как наиболее эффективные, наглядные и понятные методы решения.
В данной статье пойдет речь об одной из многих экономических моделей, рассматриваемых в образовательном процессе и о возможном ее решении графоаналитическим методом, синтезирующим графические построения и аналитические расчеты.
Постановка задачи взята из [2]. Предприятие может выпускать два вида изделий. На их изготовление идет два вида ресурсов. Запасы ресурсов на предприятии, плановые нормы их расхода 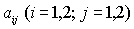
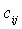
Нормы расхода на одно изделие вида
Из-за брака в производстве расход ресурсов зависит от объема 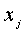
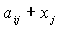
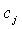
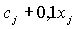
Так как 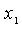
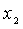
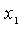
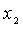
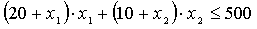
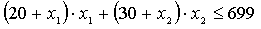
Составим функцию прибыли по формуле: П=Ц-С. Таким образом, полная прибыль от производства 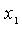
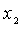
Итак, математическая модель задачи имеет вид:
Данная задача относится к задаче нелинейного программирования, т.к. переменные 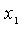
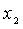
В системе ограничений выделим в левой части неравенств полные квадраты, приведем уравнение кривой второго порядка к каноническому виду:
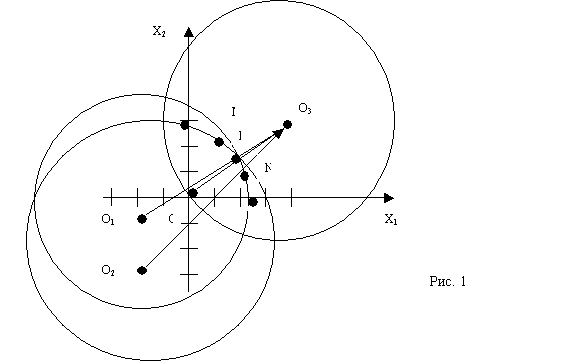
Данные кривые второго порядка представляют собой окружности, с центрами в точках О1(-10;-5) и О2(-10;-15) и радиусами R1=25 и R2=32 соответственно. Построим множество решений задачи – криволинейную область ОАВС (рис 1).
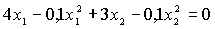
Данная кривая – окружность с центром в точке О3(20;15) и радиусом R3=25. Определим направление ( в точке О(0;0)), в котором целевая функция возрастает (т.к. необходимо найти максимум этой функции) – это направление указывает вектор- градиент целевой функции. 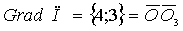
Таким образом, можно сделать вывод, что данному предприятию, в соответствующих экономических условиях, необходимо выпускать 12,63 тыс.шт. изделий вида А и 7,63 тыс.шт. изделий вида В, максимальная прибыль предприятия при этом составит порядка 51,63362 ден.ед.
Заметим, что решение задач нелинейного программирования графическими методами на практических занятиях по исследованию операций, либо какой-либо другой экономико-математической дисциплине, является лучшей адаптированной схемой к построению наиболее приближенным к современным экономико-математическим моделям промышленности, и довольно не сложным и понятным для нынешнего студенчества методам построения решения. Данные методы используют достаточно большой объем материала аналитической геометрии и дифференциального исчисления для реализации подобных моделей. Тем не менее, следует отметить, что графоаналитический метод решения соответствующих моделей легко программируется и может также использоваться при выполнении курсовых и дипломных проектов для студентов старших курсов.
1. Ляшенко И.Н., Карагодова Е.А., Черникова Н.В., Шор Н.З. Линейное и нелинейное программирование. Киев, «Высшая школа», 1975. 348-350с.
2. Сборник задач и упражнений по высшей математике: Мат. программирование: Учеб.пособие / А.В.Кузнецов, В.А.Сакович, Н.И.Холод и др.; 2-е изд.,перераб. и доп.- Мн.:Выш.шк.,2002. 271-278с.
Источник
Графический метод решения задач нелинейного программирования
Чтобы найти ее оптимальное решение, нужно выполнить следующие действия:
- Найти ОДР, определяемую ограничениями задачи. Если окажется, что эта область пуста, то это означает, что задача не имеет решения.
- Построить семейство линий уровня целевой функции f(х1, х2) = C при различных значениях числового параметра С.
- При решении задачи на минимум определить направление убывания, а для задачи на максимум — направление возрастания линий уровня ЦФ.
- Найти точку ОДР, через которую проходит линия уровня с наименьшим в задаче на минимум (соответственно, наибольшим в задачи на максимум) значением параметра С. Эта точка будет оптимальным решением. Если ЦФ не ограничена снизу в задаче на минимум (сверху — в задаче на максимум), то это означает, что задача не имеет оптимального решения.
- Найти координаты точки оптимума и определить в ней значение ЦФ.
Отметим, что в отличие от задачи ЛП точка оптимума в задаче НП не обязательно находится на границе ОДР. Ею также может быть внутренняя точка этого множества.
Пример . В задаче выпуклого программирования требуется:
- найти решение графическим методом;
- написать функцию Лагранжа и найти ее седловую точку, используя решение, полученное графически.
F(X) = x1 2 +(x2-2) 2
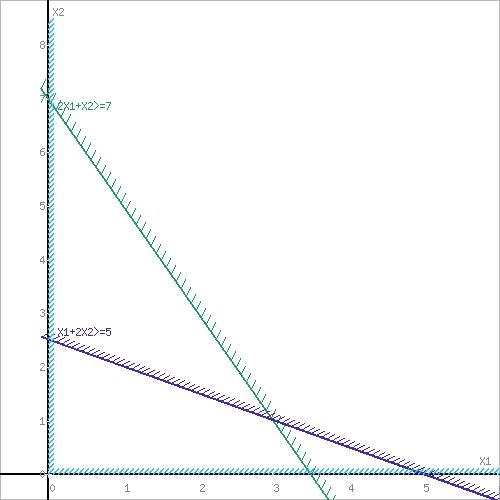
2x1+x2 ≥ 7
x1+2x2 ≥ 5
Решение. 1) Строим два ограничения, тем самым определяя ОДР. Можно использовать этот калькулятор. Также удобно строить ограничения через этот сервис.
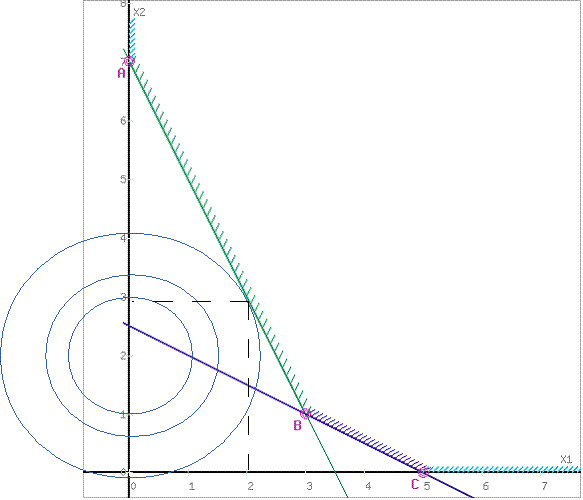
Затем строим функцию цели. В данном случае это окружность.
Поскольку задача минимума, то ищем первое касание линии уровня области ОДР. В данном случае это точка пересечения с прямой 2x1+x2-7=0.
Найдем точку пересечения. Для этого построим уравнение касательной, проходящей через центр окружности O(0;2) и перпендикулярно прямой 2x1+x2-7=0 (можно использовать этот калькулятор). Получаем: 2x2-x1-4=0. Решая систему уравнений:
2x1+x2-7=0
2x2-x1-4=0,
получаем: x1=2, x2=3.
2) Найдем экстремум функции F(X) = x1 2 +(x2-2) 2 , используя калькулятор Функция Лагранжа :
L( X , λ )=F( X )+∑(λi·φi)
где F( X ) — целевая функция вектора X; φi(X) — ограничения в неявном виде (i=1..n)
В качестве целевой функции, подлежащей оптимизации, в этой задаче выступает функция: F(X) = x1 2 +(x2-2) 2
Перепишем ограничение задачи в неявном виде:
φ1(X) = 7 — (2*x1+x2) = 0 (X1)
φ2(X) = 5 — (x1+2*x2) = 0 (X2)
Составим вспомогательную функцию Лагранжа: L(X, λ) = x1 2 +(x2-2) 2 — λ1*(7 — (2*x1+x2)) — λ2*(5 — (x1+2*x2))
Необходимым условием экстремума функции Лагранжа является равенство нулю ее частных производных по переменным хi и неопределенным множителям λ.
Составим систему:
∂L/∂x1 = 2*λ1+λ2+2*x1 = 0
∂L/∂x2 = λ1+2*λ2+2*x2-4 = 0
∂L/∂λ1 = 2*x1+x2-7 = 0
∂L/∂λ2 = x1+2*x2-5 = 0
Решив данную систему, получаем:
а) для случая X1: x1 = λ1/2 + λ2 + 2; x2 = 7 — 2x1
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2; x1 = 2; x2 = 3.
Поскольку λ2 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(2;3)=5
б) для случая X2: x2 = λ1/2 + λ2 + 2; x1 = 5 — 2x2
Откуда можно найти такие λ1 ≥ 0, λ2 ≥ 0. Пусть λ2 = 0. Тогда λ1 = 2/5; x1 = 11/5; x2 = 3/5.
Поскольку λ1 ≥ 0, то данное решение удовлетворяет условиям Куна-Таккера. Zmin(11/5;3/5)=6.8
Минимальное значение составит Zmin(2;3)=5.
Источник
Графоаналитический способ решения задач
Определение пропускной способности трубопровода по заданным параметрам его и жидкости, а также определение минимального диаметра трубопровода по заданным напору, параметрам жидкости и трубопровода, пропускной способности проводится графоаналитическим методом.
Рассмотрим алгоритм решения задач этого типа на примере первой задачи.
Графоаналитический способ решения основан на предварительном построении графической зависимости hT=f(Q) — гидравлической характеристики трубопровода. Для этого:
1. Последовательно задаемся рядом произвольных значений Q.
2. Находим соответствующие средние линейные скорости ω.
3. Рассчитываем соответствующие параметры Re.
4. Рассчитываем соответствующие параметры λ.
5. Для каждого принятого значения Q находим потери напора hT.
6. По полученным данным строим график hT = f(Q).
7. Отложив на оси ординат известное значение H, на оси абсцисс находят соответствующее ему искомое значение Q.
Аналогично решается и вторая задача:
Задаются рядом d, находят для них hT, строят график hT = f(d) и по заданной величине H по графику находят соответствующее ему значение d.
Потери напора на трение в трубопроводе определяются по формуле Дарси-Вейсбаха (70).
Разновидностью этого выражения, часто применяемой при технологических расчетах трубопроводов, является формула академика Лейбензона:

где Q и ν — соответственно объемный расход и кинематическая вязкость перекачиваемой жидкости;
β, А, m- коэффициенты, зависящие от режима течения жидкости.
Формула (90) в явной форме выражает зависимость h от Q и получается из выражения (70) при условии, что λ определяется выражением вида

Формулы для расчета коэффициента гидравлического сопротивления в зависимости от режима течения приведены в табл. 8.
Потеря напора на единицу длины трубопровода называется гидравлическим уклоном:

Для наглядности и представления о гидравлическом уклоне сделаем построение гидравлического треугольника: отложим от начальной А’ и конечной B’ точек на профиле трассы трубопровода статические (пьезометрические) напоры 

Из построения следует, что гидравлический уклон является тангенсом угла наклона этой прямой к горизонту:

то есть i = const.
Величина 
Таблица 8
Формулы для расчета коэффициента гидравлического сопротивления
| Ламинарный режим | Турбулентный режим |
| Re Перед началом гидравлического расчета исследуется профиль трассы трубопровода для определения на нем перевальных точек и нахождения его расчетной длины. Эта длина может быть значительно меньше геометрической, а перевальная точка не обязательно является наивысшей точкой трассы. Достаточно закачать жидкость на перевальную точку, чтобы она самотеком достигла конца трубопровода. Гидравлические расчеты сложных трубопроводов Различают четыре категории сложных трубопроводов. I. Коллектор постоянного диаметра с распределенным по длине отбором продукции (раздаточный коллектор в резервуарах, отстойниках, сепараторах). II. Сборный коллектор переменного диаметра с распределенным по длине поступлением продукции (система сбора скважинной продукции). III. Коллектор с параллельным участком трубопровода (байпас на водоводах). IV. Замкнутый коллектор (кольцевой водовод). Источник |