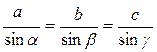Решение задач геометрическим способом системы сходящихся сил

Решение задач на равновесие геометрическим способом

Геометрическим способом удобно пользоваться, если в системе три силы. При решении задач на равновесие тело считать абсолютно твердым (отвердевшим).

Порядок решения задач:

1. Определить возможное направление реакций связей.

2. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу кон­тура.)

3. Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб.

4. Для уточнения решения рекомендуется определить величины векторов (сторон многоугольника) с помощью геометрических зави­симостей.

Решение задач на равновесие плоской системы

Сходящихся сил аналитическим методом

Непосредственное применение условий равновесия в геомет­рической форме дает наиболее простое решение для системы трех сходящихся сил. При наличии в системе четырех и более сил рациональнее применять аналитический метод, который являет­ся универсальным и применяется чаще всего. При аналитичес­ком методе решение этих задач выполняется на основе уравне­ний равновесия по следующему плану:

первый этап — выделяют объект равновесия тело или точ­ку, где пересекаются линии действия всех сил, т. е. точку, равно­весие которой в данной задаче следует рассмотреть;

второй этап — к выделенному объекту равновесия приклады­вают заданные силы;

третий этап — выделенную точку или тело освобождают от свя­зей, их действие заменяют реакциями;

четвертый этап — выбирают координатные оси и составляют уравнения равновесия;

пятый этап — решают уравнения равновесия;

шестой этап — проверяют правильность решения.

В задачах стати­ки часто приходится определять реакции стержней. Необходимо установить, как действуют растягивающие и сжимающие силы в стержнях на точки крепления стержней или узлы. Когда стер­жень MN растянут

(рис. 5, а), его реакции на точки крепления направлены от этих точек М и N

внутрь стержня. Когда стержень сжат, его реакции направлены к точкам закрепления, т, е. наружу (рис, 5, б). Следовательно, можно сказать, что в растянутом стержне реакции направлены от узлов внутрь стержня, в сжатом к узлам наружу от стержня, по аналогии с деформированной пружиной.

Часто при решении задач трудно заранее определить направ­ление реакций стержней. В этих случаях удобно считать стерж­ни растянутыми и их реакции направлять от узлов.

Если реше­ние задачи даст значение реакции со знаком минус, то в действи­тельности имеет место не растяжение, а сжатие. Таким образом, реакции растянутых стержней будут положительными, а сжатых — отрицательными.

Пример 1. Груз подвешен на стержнях и находится в равнове­сии. Определить усилия в стержнях (рис. 6а).

1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис.6а).

Определяем возможные направления реакций связей «жесткие стержни».

Усилия направлены вдоль стержней.

2. Освободим точку А от связей, заменив действие связей ихреакциями

3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в не­котором масштабе.

Из концов вектора F проводим линии, параллельные реакциям

Пересекаясь, линии создадут треугольник (рис. 6в). Зная мас­штаб построений и измерив длину сторон треугольника, можно опре­делить величину реакций в стержнях.

4. Для более точных расчетов можно воспользоваться геометри­ческими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная

Для данного случая:

; определим реакцию R₁: ;

;

, определим реакцию R₂: ;

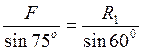
З а м е ч а н и е. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.

Пример 2. Решение задач на равновесие плоской системы сходящихся сил

Дано: Груз подвешен на стержнях и канатах и находится в равновесии. Определить реакции стержней АВ и ВС. (рис. 7).

Рис.7

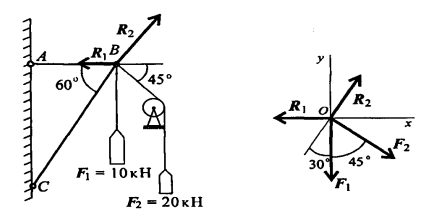
1. Определим вероятные направления реакций. Мысленно убираем стержень АВ, при этом стержень СВ опускается, следовательно точка В отодвигается от стены: назначение стержня АВ — тянуть точку В к стене.

Если убрать стержень СВ, точка В опустится, следовательно, стержень СВ поддерживает точку В снизу — реакция направлена вверх.

2. Освободим точку В от связей.

Пример 3. К кронштейну АВС в точке В подвешены два груза: груз g1 — 600 Н непосредственно и груз g ₂ = 400 Н через отводной блокD (рис. 9, а). Определить реакции стержней АВ и ВС кронштейна.

В точке В пересекаются линии действия заданных сил G 1 и G ₂ и искомых реакций стержней АВ и СВ, поэтому выделяем узел В (рис. 8, б), который в данной задаче рассматривается как объект равновесия. Прикладываем к этому узлу заданные силы G 1, направленную вертикально, и G ₂, направленную вдоль троса. При этом учитываем, что неподвижный блок D изменяет направление силы, но не влияет на ее значение. Освобождаем узел В от связей, которые осуществляются стержнями АВ и ВС. Прикладываем вместо них реакции стержней ri и R _2, направляем их вдоль стержня от узла, т. е. полагаем, что оба стержня АВ и ВС растянуты. Выбираем координатные оси х и у (при выбранном направлении осей большинство проекций имеют знак плюс) и составляем уравнения равновесия:

1). Σ Fi_x = 0; R 1- G₂ cos 45° + R₂ cos 45° = 0;

Решив уравнения равновесия, находим:

R 1 = G₂cos45° — R ₂соз45° = 400 · 0,707 — (-1249) 0,707 = 1166 Н.

Знак минус перед численным значением реакции R2показывает, что стер­жень ВС не растянут, как предполагалось, а сжат.

Задание 1

1	2
3	4
5	6
7	8
9 F1 F2	10 F1 F2

Таблица1 –Данные по вариантам

Вариант	№ схемы	F1	F2	Вариант	№ схемы	F1	F2
1	1	6	7,4	16	6	7	9
2	2	4,2	10	17	7	11	6,2
3	3	8	6,2	18	8	14	8,4
4	4	12	12	19	9	8,5	10
5	5	3	12,6	20	10	7,2	7
6	6	4.5	10	21	1	10	6.5
7	7	4,6	7,2	22	2	6,8	4,6
8	8	8.2	11	23	3	12	5.2
9	9	5,4	6,8	24	4	13,6	8,4
10	10	4,8	7	25	5	14	6,8
11	1	9	11	26	6	12,6	9
12	2	11	14	27	7	14	12
13	3	5	8,5	28	8	7,5	5,8
14	4	12	7,2	29	9	9,8	10,5
15	5	14	10	30	10	14	12

Контрольные вопросы

1. Определить модуль равнодействующей системы сходящихся сил, если проек­ции слагаемых векторов равны: F_lx = 50 Н; F_2x = -30 Н; F_3x = 60 Н; F_4x = 70 Н;

2. В каком из указанных случаев плос­кая система сходящихся сил уравновешена?

3. Какая из приведенных ниже систем уравнений равновесия справедлива для изображенной на рис.9 системы сходящихся

4. По изображенным многоугольникам сил (рис. 10) решите, сколько сил входит в каждую систему, и какая из них уравновешена. (Обратить внимание на направление векторов.)

Рис.10

Практическое занятие № 02

Тема : Определение опорных реакций балок

Цель: Научиться составлять расчетные схемы балок и определять их опорные реакции.

Входной контроль

1. Пара сил и ее действие на тело.

2. Шарнирно-подвижная опора

3. Жесткая заделка (защемление)

Теоретический материал

Виды нагрузок

По способу приложения нагрузки делятся на сосредоточенные и распределенные. Если реально передача нагрузки происходит на пренебрежимо малой площадке (в точке), нагрузку называют сосре­доточенной.

Часто нагрузка распределена по значительной площадке или ли­нии (давление воды на плотину, давление снега на крышу и т.п.), тогда нагрузку считают распределенной.

В задачах статики для абсолютно твердых тел распределен­ную нагрузку можно заменить равнодействующей сосредоточенной силой (рис. 1).

q — интенсивность нагрузки; l — длина стержня;

G = ql равнодействующая распределенной нагрузки.

Дата добавления: 2020-04-08 ; просмотров: 3864 ; Мы поможем в написании вашей работы!

Источник

Презентация по технической механике на тему «Плоская система сходящихся сил. Определение равнодействующей геометрическим способом»

Описание презентации по отдельным слайдам:

ТЕМА УРОКА: «Плоская система сходящихся сил. Определение равнодействующей геометрическим способом»

Плоская система сходящихся сил Система сил, линии действия которых пересекаются в одной точке, называется сходящейся (рис. 2.1). Необходимо определить равнодействующую системы сходящихся сил (F1; F2; F3;. . ; Fn), п — число сил, входящих в систему. По следствию из аксиом статики, все силы системы можно переместить вдоль линии действия, и все силы окажутся приложенными в одной точке.

Равнодействующая сходящихся сил. Равнодействующую двух пересекающихся сил можно определить с помощью параллелограмма или треугольника сил (4-я аксиома) (рис. 2.2).

Используя свойства векторной суммы сил, можно получить равнодействующую любой сходящейся системы сил, складывая последовательно силы, входящие в систему. Образуется многоугольник сил (рис. 2.3). Вектор равнодействующей силы соединит начало первого вектора с концом последнего. При графическом способе определения равнодействующей век-торы сил можно вычерчивать в любом порядке, результат (величина и направление равнодействующей) при этом не изменится. Вектор равнодействующей направлен навстречу векторам сил слагаемых. Такой способ получения равнодействующей называют геометрическим. Замечание. При вычерчивании многоугольника обращать внимание на параллельность сторон многоугольника соответствующем векторам сил.

Порядок построения многоугольника сил: Вычертить векторы сил заданной системы в некотором масштабе один за другим так, чтобы конец предыдущего вектора совпадал с началом последующего. Вектор равнодействующей замыкает полученную ломаную линию; он соединяет начало первого вектора с концом последнего и направлен ему навстречу. При изменении порядка вычерчивания векторов в многоугольнике меняется вид фигуры. На результат порядок вычерчивания не влияет.

Условие равновесия плоской системы сходящихся сил. При равновесии системы сил равнодействующая должна быть равна нулю, следовательно, при геометрическом построении конец последнего вектора должен совпасть с началом первого. Если плоская система сходящихся сил находится в равновесии, многоугольник сил этой системы должен быть замкнут. Если в системе три силы, образуется треугольник сил.

Решение задач на равновесие геометрическим способом Порядок решения задач: Определить возможное направление реакций связей. Вычертить многоугольник сил системы, начиная с известных сил в некотором масштабе. (Многоугольник должен быть замкнут, все векторы-слагаемые направлены в одну сторону по обходу контура.) Измерить полученные векторы сил и определить их величину, учитывая выбранный масштаб. Для уточнения решения рекомендуется определить величины, векторов (сторон многоугольника) с помощью геометрических зависимостей.

Пример 1. Груз подвешен на стержнях и находится в равновесии. Определить усилия в стержнях (рис. 2.5, а). Решение 1. Усилия, возникающие в стержнях крепления, по величине равны силам, с которыми стержни поддерживают груз (5-я аксиома статики) (рис. 2.5, а). Определяем возможные направления реакций связей «жесткие стержни». γ = 1800 – 600 – 450 Усилия направлены вдоль стержней.

2. Освободим точку А от связей, заменив действие связей их реакциями (рис. 2.5, б). 3. Система находится в равновесии. Построим треугольник сил. Построение начнем с известной силы, вычертив вектор F в некотором масштабе. Из концов вектора F проводим линии, параллельные реакциям и R1 и R2. Пересекаясь, линии создадут треугольник (рис. 2.5, в). Зная масштаб построений и измерив длину сторон треугольника, можно определить величину реакций в стержнях.

Для более точных расчетов можно воспользоваться геометрическими соотношениями, в частности теоремой синусов: отношение стороны треугольника к синусу противоположного угла — величина постоянная: Замечание. Если направление вектора (реакции связи) на заданной схеме и в треугольнике сил не совпало, значит, реакция на схеме должна быть направлена в противоположную сторону.

Пример 2. Груз подвешен на стержнях и канатах и находится в равновесии. Определить усилия в стержнях (рис. 2.6, а). Решение 1. Нанесем на схему возможные направления усилий, приложенных в точке А. Реакции стержней — вдоль стержней, усилие от каната — вдоль каната от точки А к точке В. 2. Груз находится в равновесии, следовательно, в равновесии находится точка А, в которой пересекаются три силы. Освободим точку А от связей и рассмотрим ее равновесие (рис. 2.6, б). Замечание. Рассмотрим только силы, приложенные к точке А. Груз растягивает канат силой 45 кН по всей длине, поэтому усилие от каната известно: Тз = 45 кН.

3. Строим треугольник для сил, приложенных в точке А, начиная с известной силы Т3. Стороны треугольника параллельны предполагаемым направлениям сил, приложенных в точке А. Образовался прямоугольный треугольник (рис. 2.6, е). 4. Неизвестные реакции стержней можно определить из соотношений в прямоугольном треугольнике:

Замечание. При равновесии векторы сил в треуголь­нике направлены один за другим (обходим треугольник по часовой стрелке). Сравним направления сил в треугольнике с принятыми в начале расчета на рис. 2.6, а. Направления совпали, следовательно, направления реакций определены верно.

Курс повышения квалификации

Охрана труда

• Сейчас обучается 94 человека из 45 регионов

Курс профессиональной переподготовки

Библиотечно-библиографические и информационные знания в педагогическом процессе

• Сейчас обучается 344 человека из 67 регионов

Курс профессиональной переподготовки

Охрана труда

• Сейчас обучается 175 человек из 48 регионов

Номер материала: ДБ-274462

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Заболеваемость ковидом среди студентов и преподавателей снизилась на 33%

Время чтения: 4 минуты

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Путин попросил привлекать родителей к капремонту школ на всех этапах

Время чтения: 1 минута

В Москве запустили онлайн-проект по борьбе со школьным буллингом

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник