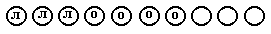Решение задач другим способом

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Решение задач разными способами – средство повышения интереса к математике.
методическая разработка по математике (1 класс) по теме

Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.

Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.

Скачать:

Предварительный просмотр:

Войнова Светлана Юрьевна, учитель начальных классов,

МОУ «СОШ №56 с углубленным изучением отдельных предметов»

Решение задач разными способами – средство повышения интереса к математике.

Люди научились считать 25-30 тысяч лет тому назад. О значении математики как предмета школьного преподавания М.В.Ломоносов в записке о преподавании физики, химии и математики пишет так:

«А математику уже затем учить следует, что она ум в порядок приводит».

Среди всех мотивов учебной деятельности самым действенным является познавательный интерес, возникающий в процессе обучения. Он не только активизирует умственную деятельность в данный момент, но и направляет ее к последующему решению различных задач.

Устойчивый познавательный интерес формируется разными средствами. Одним из них является решение задач разными способами.

Большие возможности для развития интереса учащихся к математике имеют задачи и их решения разными способами. Для кого из ребят интересна математика? Да математику любят в основном те ученики, которые умеют решать задачи, научив их решать задачи разными способами, мы окажем существенное влияние на их интерес к предмету, на развитие мышления и речи.

Однако в практике обучения математике различные способы решения ещё не заняли достойного места. Причин этому много, и в частности, недостаточная ориентация на эту работу в учебниках, методических пособиях для учителей. Учитель поэтому зачастую не владеет теми приёмами, с помощью которых можно отыскать другие способы решения. А без этого невозможно и детей научить находить разные способы решения, трудно использовать эти способы решения для других целей обучения и воспитания.

В начальном курсе математики текстовые задачи могут быть решены различными способами : алгебраическим, практическим, графическим, табличным, схематическим, комбинированным.

Рассмотрим различные способы решения текстовых задач на конкретных примерах.

Начальный курс математики ставит своей основной целью научить младших школьников решать задачи арифметическим способом, который сводится к выбору арифметических действий, моделирующих связи между данными и искомыми величинами. Решение задач оформляется в виде последовательности числовых равенств, к которым даются пояснения, или числовым выражением.

Задача. «Утром ушли в море 20 маленьких и 8 больших рыбачьих лодок, 6 лодок вернулись. Сколько лодок с рыбаками должно вернуться?»

I способ. 1. 20+8=28(л.) ушли в море.

2. 28-6=14(л.) должны вернуться.

II способ. 1. Сколько больших лодок должно вернуться? 20-6=14(л.)

2. Сколько всего лодок должно вернуться? 14+8=22(л.)

III способ. 1. Сколько маленьких лодок должно вернуться? 8-6=2(л.)

2.Сколько всего лодок должно вернуться? 20+2=22(л.)

Ответ: должно ещё вернуться 22 лодки. Задача решена различными арифметическими способами.

Если у учащихся нет навыков решения задач различными арифметическими способами или вызывает затруднение их нахождение, можно предложить следующие методические приёмы:

1. разъяснение плана решения задачи;

2. пояснение готовых способов решения;

3. соотнесение пояснения с решением;

4. продолжение начатых вариантов решения;

5. нахождение «ложного» варианта решения из числа предложенных.

Текстовые задачи решаются либо синтетическим методом (вычисления в прямом порядке, от числовых данных условия к числовым результатам, о которых спрашивается в задаче), либо аналитическим (вычисления в обратном порядке с рассуждениями, идущими от вопроса задачи). Примерами этих последних являются задачи о «задуманном числе», а также задачи на части. Естественным оформлением решения таких задач служит составление уравнения – алгебраический метод. Он состоит из следующих шагов: 1.Введение неизвестного. 2.Выражение через это неизвестное величин, о которых говорится в задаче. 3.Составление уравнения. 4.Решение уравнения. 5.Осмысление результата и формулирование ответа.

Задача: «У Иры втрое больше наклеек, чем у Кати, а у Кати на 20 наклеек меньше, чем у Иры. Сколько наклеек у Кати?».

Вначале составим схему уравнения, содержащую не только математические знаки, но и естественные слова.

( Ирины наклейки) – (Катины наклейки) = 20 наклеек.

Получилась вспомогательная модель задачи – частичный перевод текста на математический язык. Введём неизвестное. Пусть х – число Катиных наклеек. Тогда число наклеек у Иры равно х 3.

Составим уравнение х * 3 – х = 20

Ответ: у Кати 10 наклеек.

При обучении алгебраическому методу решения текстовых задач полезно дополнить схему решения самым первым шагом – составлением схемы уравнения, в которую включаются как математические символы, так и нематематические записи и даже рисунки.

Это способ решения задачи с помощью чертежа.

Задача: «Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?»

лещи окуни щуки

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

Построение чертежа помогает найти другой арифметический способ решения задачи.

Задача: «На одной машине увезли 28 мешков зерна, на другой на 6 мешков больше, чем на первой, а на третьей на 4 мешка меньше, чем на второй. Сколько мешков зерна увезли на третьей машине?»

I способ. 1. 28+6=34 (мешка) – увезли на второй машине.

2. 34-4=30 (мешка)- увезли на третьей машине.

Ответ : на третьей машине увезли 30 мешков зерна.

Если же мы построим чертеж к этой задачи, то легко найдем другой арифметический способ решения.

1. На сколько больше мешков увезли на третьей машине, чем на первой? 6-4=2(мешка)
2. Сколько мешков увезли на третьей машине? 28+2=30 (мешков)

Ответ: на третьей машине увезли 30 мешков зерна.

Из приведенных примеров следует вывод: графическое оформление задачи может определить ход мыслительного процесса и является средством выявления различных способов решения одних и тех же задач. При этом легче усматриваются разные логические основы, содержащиеся в условии задачи; такие способы определяются анализом наглядного сопровождения задачи, на которые учащиеся направляются постановкой учителем соответствующих заданий.

Задача: «В 6 банок поровну разложили 12 кг варенья. Сколько надо таких же банок, чтобы разложить 24 кг варенья?»

В данном случае логическая основа задачи проявляется на двух уровнях – открытом и скрытом, т. е. здесь две логические основы. В первом случае направление мыслительного процесса определяется вопросами:

1. Сколько кг варенья помещается в одну банку? 12:6=2(кг)
2. Сколько банок потребуется для 24 кг варенья? 24:2=12(б.)

Во втором случае ход того же процесса определяется другими вопросами:

1.Во сколько раз больше стало варенья? 24:12=2(раза)

Если варенья стало в два раза больше, значит, и банок потребуется в два раза больше.

2.Сколько потребуется банок? 6 * 2=12(б.)

Ответ: потребуется 12 банок.

При решении некоторых задач хорошим подспорьем является табличная форма.

Задача: «У Саши в коллекции 8 жуков и пауков. У всех насекомых 54 ноги. У одного жука 6 ног, а у одного паука – 8ног. Сколько жуков и сколько пауков у Саши в коллекции?»

Источник

Нестандартные решения сложных задач

Меня интересуют различные методы системного и творческого мышления, которое можно использовать в реальной жизни для решения сложных задач. О нескольких методах расскажу в данной статье.
Недавно прочитал книгу Торп С. — Учебник креативного мышления. Простой подход к нестандартным решениям – 2010. В ней предлагается интересный подход для развития навыков решения сложных задач.

Основная мысль автора – чтобы решать сложные задачи, нужно сворачивать с колеи шаблонного мышления, нарушать правила, которые зачастую нам не дают взглянуть на проблему шире. Вот что пишет автор:

Неспособность разрешить какую-то проблему вполне может объясняться тем, что вы застряли в «колее» правил. Мы все живем по правилам — укоренившимся в нас шаблонам мышления, которые ошибочно принимаем за истину. Наши правила формируются естественным образом в результате многократного использования одних и тех же идей. Следуя правилам, мы постепенно увязаем в глубокой «колее», и тогда любые неординарные идеи остаются вне нашего поля зрения.

Как нарушать правила, отлично показано на примере игры «Крестики-нолики».
Многие неразрешимые проблем похожи на игру в «крестики-нолики»» Выигрыш кажется невозможным, как бы ты не играл. Однако нарушив (или расширив) правила можно получить победу множеством путей.

Ход вне очереди

В «крестики-нолики» выиграть очень просто, если делать ходы вне очереди! Конечно в контексте крестиков-ноликов, нарушение правил – это обман. Однако речь идет не о моральных принципах, а о правилах, которые предписывают нам, как следует решать проблему.

Если правила не работают, то почему бы не сыграть на опережение, делая дополнительные ходы.
Мало кому приходит в голову сделать ход вне очереди в реальном мире, но, в сущности, этот прием используется с незапамятных времен. Например, после одного из сражений гражданской войны в Америке генерал Роберт Ли объявил своим офицерам, что генерал Грант двинется на Спотсильванию, так как это наилучшее для него решение. Ли разработал кратчайший маршрут к этому пункту и приказал войскам двигаться туда. Войска Ли сделали, так сказать, ход вне очереди и прибыли в Спотсильванию прежде, чем туда смогла добраться армия Гранта.

Ходы вне очереди — распространенное явление в мире бизнеса. Когда изготовители Тайленола узнали, что аналогичное обезболивающее средство Датрил будет продаваться со значительной скидкой, они сделали ход вне очереди. Они установили цену ниже стоимости Датрила еще до того, как изготовители последнего смогли объявить о своей цене. Рекламная кампания нового лекарства провалилась, и Тайленол удержал свои позиции на рынке.

Мы в компании, часто играем на опережение – ещё на предварительном изучении объекта автоматизации разрабатываем прототип системы. Такой подход нам позволяет глубже понять, что нужно сделать, а заказчику увидеть серьёзность наших намерений.

Используйте активы соперника

Выстроить в ряд три значка совсем не трудно, если к своим двум ноликам прибавить чужой крестик. Зачем ограничивать себя собственными ресурсами? )

Адмирал военно-морского флота США Гарри Ярнелл был первым, кто разработал план нападения японцев на Перл-Харбор. Он определил наиболее перспективные направления и стратегию атаки. В 1932 году он даже провел показательные учения с участием двух авианосцев США. Императорский военно-морской флот Японии превратил план американского адмирала в собственную успешную атаку на базу ВМС США. Японцы не постеснялись воспользоваться американским планом сражения. Если план эффективен, осознано используйте его, независимо от источника.

В шашках и шахматах победная комбинация основывается на расположении, как своих фигур, так и противника, причем именно использование фигур противник зачастую является ключевым элементом победного плана.
В бизнесе предприниматели часто изучают что сдали конкуренты, учитывают их ошибки и создают более прибыльную систему.

Проявите гибкость (и правильно ставьте задачи)

Вы сможете выиграть в «крестики-нолики» или разрешить другие сложные задачи, если примените гибкое определение термина «победа». Позвольте вашему ряду изогнуться, и победа у вас в кармане. Иногда определенные нами условия победы слишком строги или не соответствуют характеру сложившейся ситуации. Измените определение успеха и решение станет возможным.
Кроме того, если задача была поставлена неправильно, то возможно никому не под силу её решить. Задача должна ставиться конструктивно, в расчете на нетривиальные решения, отличные от ваших первоначальных ожиданий. Деструктивная постановка задач связана с таким количеством условий и ограничений, что достижение цели оказывается за пределами человеческих возможностей. Примером деструктивной постановки задачи может быть желание «летать, махая руками, словно крыльями».
При конструктивной постановке задачи приемлемым будет любое решение, позволяющее вам «оторваться от земли». Правильная постановка задачи расширяет диапазон возможных решений.

Сотрудничайте

Правило, ведущее к обязательному проигрышу одной стороны, может оказаться самым большим препятствием на пути к победе любого из участников игры. Сотрудничество с соперником может обеспечить выигрыш вам обоим.
Однажды я услышал фразу на всегда запавшую мне в душу: «В одного можно вырастить только супер-картошку!!». Имеется ввиду, что для решения действительно сложных задач нужна команда и желание сотрудничать.

Пробуйте решать сложные проблемы – нарушайте правила!

Источник