Решение задач алгебраическим способом примеры
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
- Главная
- 9-Класс
- Алгебра
- Видеоурок «Алгебраический способ решения текстовых задач»
Существует несколько способов решения текстовых задач:
• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;
• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;
• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;
• схематический способ – это способ решения текстовой задачи с помощью схем;
• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.
Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели.
В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи.
В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи.
В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры.
В схематическом способе математической моделью является схема, с помощью которой находят решение задачи.
В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.
На этом занятии более подробно будет рассмотрен алгебраический способ решения задачи.
Решить текстовую задачу алгебраическим способом означает:
1. Ввести удобную переменную выразить через неё неизвестные величины.
2. По явным условиям, описанным в задаче, составить уравнение или неравенство.
3. Решить уравнение или неравенство
4. Выбрать из всех найденных решений те, которые подходят по смыслу задачи, то есть удовлетворяют неявным условиям задачи и, таким образом, найти ответ на главный вопрос задачи. Рассмотрим методику алгебраического способа решения текстовых задач с помощью уравнений и неравенств.
1 этап. Арифметическая краткая запись условий задачи.
Цель этого этапа: осмысление задачи.
Форма записи: схематический чертёж или таблица всех известных и неизвестных данных задачи.
• этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями;
• на этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно «увязать» все известные и неизвестные величины в таблицу данных задачи или составить чертёж; неизвестные величины удобно обозначать знаком «?», а «главный вопрос» задачи для того, чтобы потом на последних этапах не запутаться и правильно найти «Ответ», так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять;
• все единицы измерения перевести в единые;
• значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры;
• Большую помощь в задачах «на движение» оказывает схематический чертёж. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.
2 этап. «Легенда» или алгебраическая краткая запись условий задачи.
Цель этого этапа: удачно выбрать переменную и выразить все неизвестные величины задачи через неё.
Форма записи: такая, как и на 1этапе, но только вместо знаков «?» везде надо записать выражения с переменной.
• обычно этот этап в оформлении задачи начинается с фразы «Пусть х ед.-…,тогда…»;
• не следует пытаться обойтись небольшим числом неизвестных; наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства;
• выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи; точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи;
• при введении переменных следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. В большинстве задач «главный вопрос» подсказывает выбор переменной.
3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).
Цель этого этапа: опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение.
• обычно этот этап в оформлении задачи начинается словами «По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).»;
• необходимо учитывать Область Допустимых Значений переменной или переменных помня условия существования уравнения или неравенства (системы уравнений или неравенств);
• для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы;S=ab–вычисление площади прямоугольника; MА=САM-вычисление массы вещества А в смеси или растворе; An=A0(1±p)n или An=A0(1±p1) … (1±pn) вычисление сложных процентов;
• если неизвестных следует брать столько, сколько потребуется, то уравнений будет cтолько, сколько получится; в простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных.
4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).
Цель: из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину.
обычно этот этап в оформлении задачи начинается фразой «По смыслу задачи х должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), и, если смысловое условие не выполнено, то найденную величину называют посторонним решением, а , если смысловое условие выполнено, то записывают единицы измерения и пояснение к найденной величине.
• т.о., не каждое решение уравнения может являться решением задачи; особенности отбора значений переменных в различных типовых задачах будут рассмотрены ниже;
• для всякой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.
Цель этого этапа: записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её «главный вопрос».
Рассмотрим полное решение задачи по указанной схеме.
Задача. Из пункта А в пункт В, расположенный в 24км от А, одновременно отправились пешеход и велосипедист. Велосипедист прибыл в пункт В на 4часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4км/ч скоростью, то на путь из А в В он затратил бы вдвое меньше времени, чем пешеход. Найти скорость пешехода.
1 этап. Арифметическая краткая запись.
По условию задачи надо определить скорость пешехода, значит, это и является «Главным вопросом» задачи.
2 этап. «Легенда» или алгебраическая краткая запись. Поскольку путь от А до В известен, то неизвестные величины–скорости пешехода и велосипедиста и время их движения. Т.к. «главный вопрос» задачи–скорость пешехода, то обозначим за переменные скорости, а время выразим через введенные неизвестные. Пусть х км/ч–скорость пешехода, у км/ч–скорость велосипедиста, тогда
В задаче описаны два условия движения пешехода и велосипедиста, значит, получим два уравнения «увязанные» с изменением времени движения.
3 этап. Составление и решение системы уравнений.
24(х + 2) – 12х – 4х(х + 2) = 0, х(х + 2)≠ 0 – ОДЗ. х2-х-12=0; По теореме Виета х1 х2=-12, х1+х2=1. Получаем два решения первого уравнения системы: х1=4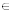
х2=-3
4 этап. Анализ решения системы уравнений.
По смыслу задачи х–положительное число, х=-3 постороннее решение,
х=4>0 =>4км/ч скорость движения пешехода.
Проверка решения задачи.
Она часто бывает полезна, но не обязательна. В задаче поставлены четыре условия существования искомой величины–скорости пешехода: 1условие–расстояние между пунктами А и В 24км; 2условие–время движения велосипедиста меньше времени движения пешехода на 4часа; 3условие–изменённая скорость велосипедиста на 4км/ч меньше фактической скорости; 4условие–изменённое время движения велосипедиста в 2раза меньше времени движения пешехода. Для проверки достоверности решения допустим выполнение двух из них при найденном решении задачи. Если два других условия при этом выполнятся, то будем считать, что задача решена верно. Если два других условия не выполнятся, то решение найдено неверно.
24км:4км/ч = 6ч – время движения пешехода; (использовали 1 условие)
6ч – 4ч = 2ч – время движения велосипедиста; (использовали 2 условие)
24км:2ч = 12км/ч – скорость движения велосипедиста;
12км/ч – 4км/ч = 8км/ч – изменённая скорость велосипедиста;
24км:8км/ч = 3ч – изменённое время движения велосипедиста; (выполнено 3 условие)
6ч:3ч = 2(раза) – отношение времени движения пешехода и велосипедиста; (выполнено 4 условие)
Все условия задачи выполнены =>скорость пешехода 4км/ч найдена верно.
5 этап. Ответ. Ответ: 4км/ч.
Таким образом, на этом занятии мы познакомились с алгебраическим способом решения текстовой задачи и разобрали методику её решения на примере задачи «на движение».
Источник
Статья на тему «Алгебраический метод решения текстовых задач для нахождения арифметического способа их решения»
Алгебраический метод решения текстовых задач для нахождения арифметического способа их решения
Решение текстовых задач младшими шк ольниками можно рассматривать как средство и как метод обучения, в ходе использования которых происходит усвоение содержания начального курса математики: математических понятий, смысла арифметических действий и их свойств, формирование вычислительных навыков и практических умений.
Учитель, руководящий процессом решения задач школьниками, должен прежде всего сам иметь решать задачи, а также владеть необходимыми знаниями и умениями учить этому других.
Умение решать задачи — основа математической подготовки учителя к обучению младших школьников решению текстовых задач.
Среди распространенных методов решения текстовых задач (алгебраический, арифметический и геометрический) наибольшее применение в начальных классах для большинства задач находит арифметический метод, включающий в себя различные способы их решения. Однако для учителя во многих случаях данный метод решения задач является более сложным, чем алгебраический. Связано это, в первую очередь, с тем , что из курса математики средней школы
практически исключен курс арифметики, который предусматривал формирование у школьников умения решать задачи арифметическим методом. Во-вторых, в вузовском курсе математики ему так же не уделяется должного внимания.
Вместе с тем необходимость в решении задач арифметическим методом диктуется запасом математических знаний младшего школьника, который не позволяет им решать большинство задач, применяя элементы алгебры.
Учитель способен, как правило, любую задачу решить алгебраически, однако далеко не каждый может решить любую задачу арифметически.
Вместе с тем указанные методы взаимосвязаны, и эту взаимосвязь учитель не только должен подмечать, но и использовать в своей работе. В данной статье на примере решения некоторых задач мы попытаемся показать связь алгебраического и арифметического методов решения задач, чтобы помочь учителю найти арифметический способ решения задачи, решив ее алгебраически.
Предварительно сделаем несколько замечаний:
1. Не всегда (и даже далеко не всегда) текстовая задача, решаемая алгебраическим методом, может быть решена арифметическим. Следует помнить, что решить задачу, применяя арифметический метод, можно в том случае, когда ее алгебраическая модель сводится к линейному уравнению или системе линейных уравнении.
2. Вид линейного уравнения не всегда «подсказывает» арифметический путь решения задачи, однако дальнейшие преобразования уравнения позволяют его найти. Решение системы линейных уравнений, на наш взгляд, практически сразу дает возможность наметить ход рассуждений для решения задачи арифметическим способом.
Пример 1. Задача сводится к уравнению
Задача. В 8 часов утра из пункта А в пункт В вышел поезд со скоростью 60 км/ч. В 11 часов из пункта В ему навстречу вышел другой поезд со скоростью 70 км/ч. В какое время поезда встретятся, если расстояние между пунктами 440 км?
Алгебраический метод приводит к уравнению: (60 + 70) х + 60 • 3 = 440 или 130х+18= 440, где х часов — время движения второго поезда до встречи. Тогда: 130 х = 440- 180= 130
Проделанные рассуждения и выкладки «подсказывают» следующий арифметический путь решения задачи. Найдем: сумму скоростей поездов (60 + 70 = 130 (км/ч), время движения первого поезда до начала движения второго поезда (11-8=3 (ч), расстояние, пройденное первым поездом за 3 часа (60 • 3 = 180 (км), расстояние, которое осталось пройти поездам до встречи (440 — 180 = = 260 (км), время движения второго поезда до встречи (260 : 130 -2 (ч)).
В дальнейшем этапы решения каждой задачи алгебраическим методом и соответствующие им этапы решения задачи арифметическим методом будем параллельно записывать в таблице, которая позволит наглядно проследить, как алгебраические преобразования в «ходе решения уравнений, являющихся моделью текстовой задачи, открывают арифметический способ решения. Так, в данном случае будем иметь следующую таблицу (см. таблицу 1).
Пусть х часов — время движения второго поезда до встречи. По условию задачи получаем уравнение:
(60+70)-х+60*3=440 или 130х+180=440
Найдем сумму скоростей поездов: 60+70=130(км/ч).
Найдем время движения первого поезда до начала движения второго поезда: 11-8=3(ч). Найдем расстояние, пройденное первым поездом за 3 часа: 60*3=180(км)
Найдем расстояние, которое осталось пройти поездам до встречи: 440-180=260(км).
Найдем время движения второго поезда: 260:130=2(ч).
Используя данные таблицы 1, получаем арифметическое решение.
= 3 (ч)- был в пути первый поезд до начала движения второго;
3 = 180 (км) — прошел первый поезд за 3 часа;
3) 440 — 180 = 260 (км) — расстояние, пройденное поездами при одновременном движении;
70 = 130 (км/ч) — скорость сближения поездов;
130 = 2 (ч) — время движения второго поезда;
6)11 + 2 = 13 (ч) — в такое время поезда встретятся.
Ответ: в 13 часов.
Пример 2. Задача сводится к уравнению вида: а 1 х +в 1 =а х+в
Задача. Школьники купили 4 книги, после чего у них осталось 40 рублей. Если бы они купили 7 таких же книг, то у них осталось бы 16 рублей. Сколько стоит одна книга?
Алгебраический метод приводит к уравнению: 4х + 40 = 7х + 16, где х — стоимость одной книги. В ходе решения данного уравнения мы проделываем следующие выкладки: 7 х — 4 х =40-16 —> Зх=24 —> х= 8, которые вместе с рассуждениями, использовавшимися при составлении уравнения, приводят к арифметическому способу решения задачи. Найдем: на сколько больше книг купили: 7-4=3 (кн.); на сколько меньше денег останется, т.е. на сколько больше денег израсходовали: 40 — 16 = 24 (р); сколько стоит одна книга: 24 : 3 = 8 (р). Проделанные рассуждения сведем в таблицу 2.
Этапы решения задачи
Этапы решения задачи арифметическим методом
Пусть х — стоимость одной книги. По условию задачи
получаем уравнение: 4х+40=7х+16.
7х-4х=40-16 (7-4)х=24 3х=24
Стоимость четырех книг и еще 40р. равна стоимости 7 книг и еще 70р.
Найдем, на сколько больше книг купили бы: 7-4=3(кн). Найдем, на сколько больше заплатили бы денег: 40-16=24(р.).
Найдем стоимость одной книги: 24:3=8(р.).
Используя данные таблицы 2, получаем арифметическое решение:
1) 7-4=3 (кн.) — на столько книг купили бы больше;
— 16 = 24 (р.) — на столько рублей заплатили бы больше;
3)24 : 3 = 8 (р.) — стоит одна книга.
Пример 3. Задача сводится к уравнению вида: ах + b x + сх = d
Задача. Турист проехал 2 200 км, причем на теплоходе проехал вдвое больше, чем на автомобиле, а на поезде в 4 раза больше, чем на теплоходе. Сколько километров проехал турист отдельно на теплоходе, автомобиле и на поезде?
Используя данные таблицы 3, получаем арифметическое решение.
Примем расстояние, которое турист проехал на автомобиле, за одну часть:
1 • 2 = 2 (ч.) – приходится на расстояние, которое преодолел турист на теплоходе;
2) 2 • 4 = 8 (ч.) – приходится на расстояние, которое преодолел турист на поезде;
3) 1+2+8=11(ч) — приходится на весь путь
Пусть х километров –расстояние, которое турист проехал на теплоходе.
По условию задачи получаем уравнение: х+2х+2*4х=2200.
Примем расстояние, которое турист проехал на автомобиле (самое меньшее), за 1 часть. Тогда расстояние, которое он проехал на теплоходе, будет соответствовать двум частям, а на поезде – 2 – 4 частям. Значит, весь путь туриста (2200 км) соответствует 1+2+8=11 (ч.).
Найдем, сколько частей составляет весь путь туриста: 1+2+8=11 (ч.).
Найдем, сколько километров приходится на одну часть: 2200:11=200 (км).
200: 11= 200 (км) — расстояние, которое преодолел турист на автомобиле;
2 = 400 (км) — расстояние, которое преодолел турист на теплоходе;
6)200 -8=1 600 (км) — расстояние, которое преодолел турист на поезде.
Ответ: 200 км, 400 км, 1 600 км.
Пример 4. Задача сводится к уравнению вида (х + а) в = сх + d .
Задача. По окончании спектакля 174 зрителя из театра разошлись пешком, а остальные поехали на трамваях в 18 вагонах, причем в каждый вагон садилось на 5 человек больше, чем было в нем мест. Если бы зрители, уезжавшие из театра на трамвае, садились в него по числу мест, то понадобилось бы еще 3 вагона, причем в последнем осталось бы 6 свободных мест. Сколько всего зрителей было в театре?
Пусть в каждом трамвае было х мест. Тогда по условию задачи имеем уравнение: (х+5)*18=х*(18+3)-6.
Преобразуем уравнение: 21х – 18х = 90+6 или 3х = 96.
В каждый вагон входило на 5 человек больше, чем было в нем мест. В 18 вагонах – на 5 * 18 = 90 человек больше. В 3 дополнительных вагона вошло 90 человек и осталось еще 6 свободных мест. Следовательно, в трех вагонах 90 + 6 = 96 мест.
Найдем количество мест в одном вагоне:
Используя данные таблицы 4, получаем арифметическое решение:
1)5•18 = 90 (чел.) — на столько человек больше, чем мест было в 18 вагонах;
90 + 6 = 96 (м.) — в трех вагонах;
96 : 3 = 32 (м.) — в одном вагоне;
32 + 5 = 37 (чел.) — было в каждом из 18 вагонов;
37 • 18 = 666 (чел.) — уехало на трамваях;
666 + 174 = 840 (чел.) — было в театре.
Ответ: 840 зрителей.
Пример 5. Задача сводится к системе уравнений вида: х+ у = а, х –у = b .
Задача. Пояс с пряжкой стоит 12 рублей, причем пояс дороже пряжки на 6 рублей.
Сколько стоит пояс, сколько стоит пряжка?
Алгебраический метод приводит к системе уравнений:
х-у=6 где х: рублей — цена пояса, у рублей — цена пряжки.
Данную систему можно решить методом подстановки: выразив одно неизвестное через другое. Из первого уравнения, подставив его значение во второе уравнение, решить полученное уравнение с одним неизвестным, найти второе неизвестное. Однако в этом случае мы не сможем «нащупать» арифметический путь решения задачи.
Сложив уравнения системы, мы сразу будем иметь уравнение 2х = 18.
Откуда находим стоимость пояса х = 9 (р.). Этот способ решения системы позволяет получить следующий арифметический ход рассуждений. Предположим, что пряжка стоит столько же, сколько и пояс. Тогда пряжка с поясом (или 2 пояса) будут стоить 12+6= 18 (р.) (так как на самом деле пряжка на 6 рублей стоит дешевле). Следовательно, один пояс стоит 18:2=9 (р.).
Если мы вычтем почленно из первого уравнения второе, то получим уравнение 2 у =6, откуда у = 3 (р.). В этом случае, решая задачу арифметическим методом, рассуждать следует так. Предположим, что пояс стоит столько же, сколько и пряжка. Тогда пряжка и пояс (или две пряжки) будут стоить 12-6=6 (р.) (так как на самом деле пояс на 6 рублей стоит дороже).
Следовательно, одна пряжка стоит 6:2=3 (р.)
Пусть х рублей – цена пояса, у рублей – цена пряжки. По условию задачи получаем систему уравнений:
Почленно сложив уравнения системы, получим: 2х = 12 + 6 2х = 18.
Пояс с пряжкой стоят 12р. И пояс дороже пряжки на 6р.
Предположим, что пряжка стоит столько же, сколько и пояс, тогда два пояса стоят 12 + 6 = 18 (р.).
Найдем цену пояса:
Используя данные таблицы 5, получаем арифметическое решение:
12+6= 18 (р.) — стоили бы два пояса, если бы пряжка стоила столько же, сколько и пояс;
2) 18:2=9 (р.) — стоит один пояс;
3) 12-9=3 (р.) — стоит одна пряжка.
О т в е т: 9 рублей, 3 рубля.
Пример 6. Задача сводится к системе уравнений вида:
ах + Ьу = с 1 х+у=с2
Задача. Для похода 46 школьников приготовили четырех- и шестиместные лодки. Сколько было тех и других лодок, если все ребята разместились в десяти лодках и свободных мест не осталось ?
Пусть х – количество четырехместных лодок, у – количество шестиместных лодок. По условию задачи имеем систему уравнений:
Умножаем обе части первого уравнения на 4.
Вычитаем ( почленно ) полученное уравнение из второго. Имеем:
(6 – 4) у = 46 – 40 или 2у = 6.
Всех лодок 10 и в них разместилось 46 школьников.
Предположим, что все лодки были четырехместными. Тогда м них разместилось бы 40 человек.
Найдем, на сколько больше человек вмещает шестиместная лодка, чем четырехместная: 6 – 4 = 2 (чел.). Найдем, скольким школьникам не хватит мест, если все лодки будут четырехместные: 46 – 40 = 6 (чел.).
Найдем количество шестиместных лодок: 6 : 2 = 3 (шт.).
Используя данные таблицы 6, получаем арифметическое решение:
1)4- 10 = 40 (чел.) — разместилось бы, если бы все лодки были четырехместными;
2) 6 — 4 = 2 (чел.) — на столько человек шестиместная лодка вмещает больше, чем четырехместная;
3)46 — 40 — 6 (чел.) — стольким школьникам не хватит места, если
все лодки четырехместные;
4) 6 : 2 = 3 (шт.) — было шестиместных лодок;
5) 10 — 3 = 7 (шт.) — было четырехместных лодок.
Ответ: 3 шестиместные лодки, 7 четырехместных лодок .
Пример 7. Задача сводится к системе уравнений вида: а х+Ь у=с1; а х +Ь у=с2
Задача. 3 ручки и 4 блокнота стоят 26 рублей, а 7 ручек и 6 таких же блокнотов стоят 44рубля. Сколько стоит блокнот?
Пусть х рублей – цена ручки, у рублей – цена блокнота. По условию задачи получаем систему уравнений:
Умножим обе части первого уравнения на 7. Получим:
21 х + 28 у = 182,
21 х + 18 у = 132.
Вычтем (почленно) из первого уравнения второе.
(28 – 18) у = 182 – 132 или 10 у = 50.
3 ручки и 4 блокнота стоят 26 рублей. 7 ручек и 6 блокнотов стоят 44 рубля.
Уравняем количество ручек в двух покупках. Для этого найдем наименьшее кратное чисел 3 и 7 (21). Тогда в результате первой покупки были куплены 21 ручка и 28 блокнотов, а второй – 21 ручка и 18 блокнотов. Найдем стоимость каждой покупки в этом случае:
26 * 7 = 182 (р.), 44 * 3 = 132 (р.).
Найдем, на сколько больше блокнотов было куплено в первый раз:
Найдем, на сколько больше заплатили бы при первой покупке:
Найдем, сколько стоит Блокнот:
Используя данные таблицы 7, получаем арифметическое решение:
1) 26 • 7 = 182 (р.) — стоят 21ручка и 28 блокнотов;
2) 44 • 3 = 132 (р.) — стоят 21ручка и 18 блокнотов;
3) 28 — 18 = 10 (шт.) — на столько блокнотов в первой покупке было бы больше, чем во второй;
4) 182 — 132 = 50 (р.) — стоят 10 блокнотов;
5) 50 : 10=5 (р.) — стоит блокнот.
Мы рассмотрели некоторые виды текстовых задач, встречающиеся в различных учебниках математики для начальных классов. Несмотря на кажущуюся простоту установления связи между алгебраическим и арифметическим методами, этот прием все же требует тщательной отработки со студентами на практических занятиях и кропотливой работы учителя в ходе самоподготовки к уроку.
Источник