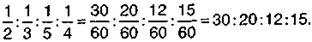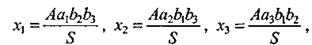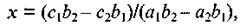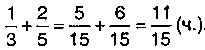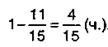Решение уравнения арифметическим способом
Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту
- Главная
- 9-Класс
- Алгебра
- Видеоурок «Алгебраический способ решения текстовых задач»
Существует несколько способов решения текстовых задач:
• арифметический способ – это способ решения текстовой задачи с помощью чисел и знаков арифметических действий сложения, вычитания, умножения и деления, то есть с помощью нескольких действий над числами, связанных между собой;
• алгебраический способ – это способ решения текстовой задачи с помощью введения переменных и составления соответствующего уравнения или неравенства, или системы уравнений или неравенств;
• геометрический способ – это способ решения текстовой задачи с помощью применения геометрических знаний;
• схематический способ – это способ решения текстовой задачи с помощью схем;
• графический способ – это способ решения текстовой задачи с помощью графиков в прямоугольной системе координат.
Каждый из этих способов предполагает перевод условий задачи на язык математики. Это действие математики называют математическим моделированием. Результат этого действия называют математической моделью. При применении различных способов решения получаются различные математические модели.
В арифметическом способе математической моделью является числовое выражение, то есть числовой пример с несколькими действиями, а конечный результат вычислений будет решением задачи.
В алгебраическом способе математической моделью чаще всего является уравнение, а решение уравнения даёт решение задачи.
В геометрическом способе математической моделью является геометрическая фигура, а решение задачи – это один из найденных элементов этой фигуры.
В схематическом способе математической моделью является схема, с помощью которой находят решение задачи.
В графическом способе математической моделью является график, построенный по условию задачи. При этом способе решением задачи являются координаты определённых точек графиков.
На этом занятии более подробно будет рассмотрен алгебраический способ решения задачи.
Решить текстовую задачу алгебраическим способом означает:
1. Ввести удобную переменную выразить через неё неизвестные величины.
2. По явным условиям, описанным в задаче, составить уравнение или неравенство.
3. Решить уравнение или неравенство
4. Выбрать из всех найденных решений те, которые подходят по смыслу задачи, то есть удовлетворяют неявным условиям задачи и, таким образом, найти ответ на главный вопрос задачи. Рассмотрим методику алгебраического способа решения текстовых задач с помощью уравнений и неравенств.
1 этап. Арифметическая краткая запись условий задачи.
Цель этого этапа: осмысление задачи.
Форма записи: схематический чертёж или таблица всех известных и неизвестных данных задачи.
• этот этап может отсутствовать, если решение задачи элементарно или она не особо усложнена условиями;
• на этом этапе решения задачи происходит понимание или осмысление её текста. Намного облегчает этот процесс умение правильно «увязать» все известные и неизвестные величины в таблицу данных задачи или составить чертёж; неизвестные величины удобно обозначать знаком «?», а «главный вопрос» задачи для того, чтобы потом на последних этапах не запутаться и правильно найти «Ответ», так как в некоторых задачах, содержащих неявный вопрос искомую величину приходится довычислять;
• все единицы измерения перевести в единые;
• значительно облегчает решение и делает задачу более понятной введение обозначений, общепринятых в физике, химии, геометрии, алгебре, экономике и так далее. Например: V,t,s-скорость, время, расстояние (длина пути или отрезка); р,V,m-плотность вещества, объём тела, масса тела; W,t,V–производительность, время работы, объём работы; a,b,P,S–две стороны прямоугольника, его периметр, его площадь; А0,р,n,An-первоначальная величина, процент её увеличения, количество увеличений, конечная величина после увеличения А0 на р процентов n раз; MА,СА,M–масса вещества А в растворе или в смеси, концентрация вещества А в растворе или смеси (доля), масса раствора или смеси; mn=10m+n–запись двузначного числа, где m,n–цифры;
• Большую помощь в задачах «на движение» оказывает схематический чертёж. Он позволяет увидеть динамику движения, а также учесть все характерные ситуации–встречи, остановки, повороты и тому подобное.
2 этап. «Легенда» или алгебраическая краткая запись условий задачи.
Цель этого этапа: удачно выбрать переменную и выразить все неизвестные величины задачи через неё.
Форма записи: такая, как и на 1этапе, но только вместо знаков «?» везде надо записать выражения с переменной.
• обычно этот этап в оформлении задачи начинается с фразы «Пусть х ед.-…,тогда…»;
• не следует пытаться обойтись небольшим числом неизвестных; наоборот, чем больше неизвестных, тем легче составлять уравнения или неравенства;
• выбирая неизвестные, мы создаём математическую модель ситуации, описанной в условии задачи; точнее, набор переменных представляет собой список параметров, определяющих эту модель, поэтому все они должны быть независимы, и все соотношения должны следовать лишь из конкретных условий задачи;
• при введении переменных следует руководствоваться принципом наибольшего удобства математической записи условий задачи, при этом искомая величина может не входить в их число. В большинстве задач «главный вопрос» подсказывает выбор переменной.
3 этап. Составление и решение уравнения или неравенства (системы уравнений или неравенств).
Цель этого этапа: опираясь на условия задачи составить уравнение или неравенство ( систему уравнений или неравенств ) и найти его (её) решение.
• обычно этот этап в оформлении задачи начинается словами «По условию задачи (выписать условия из текста задачи), значит,…(запись уравнения или неравенства).»;
• необходимо учитывать Область Допустимых Значений переменной или переменных помня условия существования уравнения или неравенства (системы уравнений или неравенств);
• для составления уравнения или неравенства (системы уравнений или неравенств) из текста задачи выбираем условие (условия), которое позволяет увязать известные и неизвестные данные задачи в формулы: S=vt-вычисление длины пути, пройденного телом; m=pV-вычисление массы тела; V=Wt-вычисление объёма работы;S=ab–вычисление площади прямоугольника; MА=САM-вычисление массы вещества А в смеси или растворе; An=A0(1±p)n или An=A0(1±p1) … (1±pn) вычисление сложных процентов;
• если неизвестных следует брать столько, сколько потребуется, то уравнений будет cтолько, сколько получится; в простейших ситуациях мы получаем уравнение (неравенство) с одной переменной или систему уравнений (неравенств), в которой число уравнений (неравенств) совпадает с числом неизвестных.
4 этап. Анализ решения уравнения или неравенства (системы уравнений или неравенств).
Цель: из всех найденных решений уравнений или неравенств (систем уравнений или неравенств) выбрать те, которые подходят по смыслу задачи и, по мере необходимости, довычислить искомую величину.
обычно этот этап в оформлении задачи начинается фразой «По смыслу задачи х должна быть величиной… (натуральной, положительной, целой, принадлежащей промежутку и так далее), и, если смысловое условие не выполнено, то найденную величину называют посторонним решением, а , если смысловое условие выполнено, то записывают единицы измерения и пояснение к найденной величине.
• т.о., не каждое решение уравнения может являться решением задачи; особенности отбора значений переменных в различных типовых задачах будут рассмотрены ниже;
• для всякой текстовой задачи полезно провести проверку её решения, причём проверять нужно соответствие полученного ответа условию задачи, а не составленным уравнениям.
Цель этого этапа: записать правильный ответ, удовлетворяющий всем описанным условиям задачи и отвечающий на её «главный вопрос».
Рассмотрим полное решение задачи по указанной схеме.
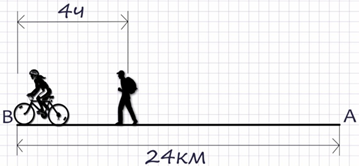
Задача. Из пункта А в пункт В, расположенный в 24км от А, одновременно отправились пешеход и велосипедист. Велосипедист прибыл в пункт В на 4часа раньше пешехода. Известно, что если бы велосипедист ехал с меньшей на 4км/ч скоростью, то на путь из А в В он затратил бы вдвое меньше времени, чем пешеход. Найти скорость пешехода.
1 этап. Арифметическая краткая запись.
По условию задачи надо определить скорость пешехода, значит, это и является «Главным вопросом» задачи.
2 этап. «Легенда» или алгебраическая краткая запись. Поскольку путь от А до В известен, то неизвестные величины–скорости пешехода и велосипедиста и время их движения. Т.к. «главный вопрос» задачи–скорость пешехода, то обозначим за переменные скорости, а время выразим через введенные неизвестные. Пусть х км/ч–скорость пешехода, у км/ч–скорость велосипедиста, тогда
В задаче описаны два условия движения пешехода и велосипедиста, значит, получим два уравнения «увязанные» с изменением времени движения.
3 этап. Составление и решение системы уравнений.
24(х + 2) – 12х – 4х(х + 2) = 0, х(х + 2)≠ 0 – ОДЗ. х2-х-12=0; По теореме Виета х1 х2=-12, х1+х2=1. Получаем два решения первого уравнения системы: х1=4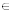
ДЗ,
х2=-3
ОДЗ. Оба решения удовлетворяют неравенству системы, т.е. ОДЗ дробно–рационального уравнения.
4 этап. Анализ решения системы уравнений.
По смыслу задачи х–положительное число, х=-3 постороннее решение,
х=4>0 =>4км/ч скорость движения пешехода.
Проверка решения задачи.
Она часто бывает полезна, но не обязательна. В задаче поставлены четыре условия существования искомой величины–скорости пешехода: 1условие–расстояние между пунктами А и В 24км; 2условие–время движения велосипедиста меньше времени движения пешехода на 4часа; 3условие–изменённая скорость велосипедиста на 4км/ч меньше фактической скорости; 4условие–изменённое время движения велосипедиста в 2раза меньше времени движения пешехода. Для проверки достоверности решения допустим выполнение двух из них при найденном решении задачи. Если два других условия при этом выполнятся, то будем считать, что задача решена верно. Если два других условия не выполнятся, то решение найдено неверно.
24км:4км/ч = 6ч – время движения пешехода; (использовали 1 условие)
6ч – 4ч = 2ч – время движения велосипедиста; (использовали 2 условие)
24км:2ч = 12км/ч – скорость движения велосипедиста;
12км/ч – 4км/ч = 8км/ч – изменённая скорость велосипедиста;
24км:8км/ч = 3ч – изменённое время движения велосипедиста; (выполнено 3 условие)
6ч:3ч = 2(раза) – отношение времени движения пешехода и велосипедиста; (выполнено 4 условие)
Все условия задачи выполнены =>скорость пешехода 4км/ч найдена верно.
5 этап. Ответ. Ответ: 4км/ч.
Таким образом, на этом занятии мы познакомились с алгебраическим способом решения текстовой задачи и разобрали методику её решения на примере задачи «на движение».
Источник
Лекция 2. Арифметический метод решения текстовых задач
1. Общие замечания к решению задач арифметическим методом.
2. Задачи на нахождение неизвестных по результатам действий.
3. Задачи на пропорциональное деление.
4. Задачи на проценты и части.
5. Задачи, решаемые обратным ходом.
1. Арифметический метод – это основной метод решения текстовых задач в начальной школе. Находит он свое применение и в среднем звене общеобразовательной школы. Этот метод позволяет глубже понять и оценить всю важность и значимость каждого этапа работы над задачей.
В некоторых случаях решение задачи арифметическим методом значительно проще, чем другими методами.
Подкупая своей простотой и доступностью, арифметический метод вместе с тем достаточно сложен, и овладение приемами решения задач этим методом требует серьезной и кропотливой работы. Большое разнообразие видов задач не позволяет сформировать универсального подхода к анализу задач, поиску пути их решения: задачи, даже объединенные в одну группу, имеют совершенно разные способы решения.
2.К задачам на нахождение неизвестных по их разности и отношению относятся задачи, в которых по известным разности и частному двух значений некоторой величины требуется найти эти значения.
Алгебраическая модель:
Ответ находится по формулам: х = ак/(к – 1), у = а/(к – 1).
Пример.В плацкартных вагонах скорого поезда на 432 пассажира больше, чем в купейных. Сколько пассажиров находится в плацкартных и купейных вагонах отдельно, если в купейных вагонах пассажиров в 4 раза меньше, чем в плацкартных?
Решение. Графическая модель задачи представлена на рис. 4.
Число пассажиров в купейных вагонах примем за 1 часть. Тогда можно найти, сколько частей приходится на число пассажиров в плацкартных вагонах, а затем, сколько частей приходится на 432 пассажира. После этого можно определить число пассажиров, составляющих 1 часть (находящихся в купейных вагонах). Зная, что в плацкартных вагонах пассажиров в 4 раза больше, найдем их число.
Запишем решение по действиям с пояснениями.
1) 1 × 4 = 4 (ч.) – приходится на пассажиров в плацкартных вагонах;
2) 4 – 1 = 3 (ч.) – приходится на разность между числом пассажиров в плацкартных и купейных вагонах;
3) 432 : 3 = 144 (п.) – в купейных вагонах;
4) 144 × 4 = 576 (п.) – в плацкартных вагонах.
Эту задачу можно проверить, решив ее другим способом, а именно:
3) 432 : 3 = 144 (п.);
4) 144 + 432 = 576 (п.).
Ответ: в купейных вагонах 144 пассажира, в плацкартных – 576.
К задачам на нахождение неизвестных по двум остаткам или двум разностям, относятся задачи, в которых рассматриваются две прямо или обратно пропорциональные величины, такие, что известны два значения одной величины и разность соответствующих значений другой величины, а требуется найти сами значения этой величины.
Ответы находятся по формулам:
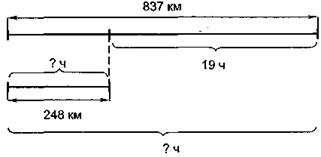
Пример.Два поезда прошли с одинаковой скоростью – один 837 км, другой 248 км, причем первый был в пути на 19 ч. больше второго. Сколько часов был в пути каждый поезд?
Решение. Графическая модель задачи представлена на рисунке 5.
Чтобы ответить на вопрос задачи, сколько часов был в пути тот или другой поезд, надо знать пройденное им расстояние и скорость. Расстояние дано в условии. Чтобы узнать скорость, надо знать расстояние и время, за которое это расстояние пройдено. В условии сказано, что первый поезд шел на 19 ч. дольше, а пройденное им за это время расстояние можно найти. Он шел лишних 19 ч. – очевидно, за это время прошел и лишнее расстояние.
Запишем решение по действиям с пояснениями:
1) 837 – 248 = 589 (км) – на столько километров больше прошел первый поезд;
2) 589 : 19 = 31 (км/ч) – скорость первого поезда;
3) 837 : 31 = 27 (ч.) – был в пути первый поезд;
4) 248 : 31 = 8 (ч.) – был в пути второй поезд.
Проверим решение задачи установлением соответствия между данными и числами, полученными при решении задачи.
Узнав, сколько времени был в пути каждый поезд, найдем, на сколько часов больше был в пути первый поезд, чем второй: 27 – 8 = 19 (ч.). Это число совпадает с данным в условии. Следовательно, задача решена верно.
Эту задачу можно проверить, решив ее другим способом. Все четыре вопроса и первые три действия остаются те же.
Ответ: первый поезд был в пути 31ч., второй поезд – 8 ч.
Задачи на нахождение трех неизвестных по трем суммам этих неизвестных, взятых попарно:
Алгебраическая модель: 
Ответ находится по формулам:
Пример.Английский и немецкий языки изучают 116 школьников, немецкий и испанский языки изучают 46 школьников, а английский и испанский языки изучают 90 школьников. Сколько школьников изучают английский, немецкий и испанский языки отдельно, если известно, что каждый школьник изучает только один язык?
Решение. Графическая модель задачи представлена на рисунке 6.
Сколько школьников изучает каждый из языков?
Графическая модель задачи показывает: если сложить численности школьников, данные в условии (116 + 90 + 46), то получим удвоенное число школьников, изучающих английский, немецкий и испанский языки. Разделив его на два, найдем общее число школьников. Чтобы найти число школьников, изучающих английский язык, достаточно из этого числа вычесть число школьников, изучающих немецкий и испанский языки. Аналогично находим остальные искомые числа.
Запишем решение по действиям с пояснениями:
1) 116 + 90 + 46 = 252 (шк.) – удвоенное число школьников, изучающих языки;
2) 252 : 2 = 126 (шк.) – изучают языки;
3) 126 – 46 = 80 (шк.) – изучают английский язык;
4) 126 – 90 = 36 (шк.) – изучают немецкий язык;
5) 126 – 116 = 10 (шк.) – изучают испанский язык.
Эту задачу можно проверить, решив ее другим способом.
1) 116 – 46 = 70 (шк.) – на столько больше школьников изучают английский язык, чем испанский;
2) 90 + 70 = 160 (шк.) – удвоенное число школьников, изучающих английский язык;
3) 160 : 2 = 80 (шк.) – изучают английский язык;
4) 90 – 80 = 10 (шк.) – изучают испанский язык;
5) 116 – 80 = 36 (шк.) – изучают немецкий язык.
Ответ: английский язык изучают 80 школьников, немецкий язык – 36 школьников, испанский язык – 10 школьников.
3. К задачам на пропорциональное деление относятся задачи, в которых данное значение некоторой величины требуется разделить на части пропорционально заданным числам. В некоторых из них части представлены явно, а в других эти части надо суметь выделить, приняв одно из значений этой величины за одну часть и определив, сколько таких частей приходится на другие ее значения.
Выделяют пять видов задач на пропорциональное деление.
1) Задачи на деление числа на части, прямо пропорциональные ряду целых или дробных чисел
К задачам данного типа относятся задачи, в которых число А (значение некоторой величины) нужно разделить на части х1, х2, х3, . хn прямо пропорционально числам а1, а2, а3, . аn.
Ответ находится по формулам:
Пример.Туристическая фирма располагает четырьмя базами отдыха, которые имеют корпуса одинаковой вместимости. На территории 1-й базы отдыха расположены 6 корпусов, 2-й – 4 корпуса, 3-й – 5 корпусов, 4-й – 7 корпусов. Сколько отдыхающих может разместиться на каждой базе, если на всех 4 базах может разместиться 2112 человек?
Решение. Краткая запись задачи показана на рисунке 7.
Чтобы ответить на вопрос задачи, сколько отдыхающих может разместиться на каждой базе, надо знать, сколько отдыхающих может разместиться в одном корпусе и сколько корпусов расположено на территории каждой базы. Число корпусов на каждой базе дано в условии. Чтобы узнать, сколько отдыхающих может разместиться в одном корпусе, надо знать, сколько отдыхающих может разместиться на всех 4 базах (это дано в условии) и сколько корпусов расположено на территории всех 4 баз. Последнее можно определить, зная из условия, сколько корпусов расположено на территории каждой базы.
Запишем решение по действиям с пояснениями:
1) 6 + 4 + 5 + 7 = 22 (к.) – расположено на территории 4 баз;
2) 2112 : 22 = 96 (ч.) – может разместиться в одном корпусе;
3) 96 × 6 = 576 (ч.) – может разместиться на первой базе;
4) 96 × 4 = 384 (ч.) – может разместиться на второй базе;
5) 96 × 5 = 480 (ч.) – может разместиться на третьей базе;
6) 96 × 7 = 672 (ч.) – может разместиться на четвертой базе.
Проверка. Подсчитываем, сколько отдыхающих может разместиться на 4 базах: 576 + 384 + 480 + 672 = 2 112 (ч.). Расхождения с условием задачи нет. Задача решена правильно.
Ответ: на первой базе может разместиться 576 отдыхающих, на второй – 384 отдыхающих, на третьей – 480 отдыхающих, на четвертой – 672 отдыхающих.
2) Задачи на деление числа на части, обратно пропорциональные ряду целых или дробных чисел
К ним относятся задачи, в которых число А (значение некоторой величины) нужно разделить на части x1i,x2,x3i, . х„ обратно пропорционально числам а1ь а2, а3. аn.
или
Ответ находится по формулам:
Пример.За четыре месяца доход зверофермы от продажи пушнины составил 1 925 000 р., причем по месяцам полученные деньги распределились обратно пропорционально числам 2, 3, 5, 4. Каков доход фермы в каждом месяце отдельно?
Решение. Для определения названных в условии доходов дан общий доход за четыре месяца, то есть сумма четырех искомых чисел, а также отношения между искомыми числами. Искомые доходы обратно пропорциональны числам 2, 3, 5, 4.
Обозначим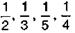 
искомые доходы соответственно через х,, х2, х3, х4. Тогда кратко задачу можно записать так, как показано на рисунке 8.
Зная число частей, приходящихся на каждое из искомых чисел, найдем число частей, заключающихся в их сумме. По данному общему доходу за четыре месяца, то есть по сумме искомых чисел и по числу частей, содержащихся в этой сумме, узнаем величину одной части, а потом искомые доходы.
Запишем решение по действиям с пояснениями:
1. Искомые доходы обратно пропорциональны числам 2, 3, 5, 4, а значит, прямо пропорциональны числам, обратным данным, то есть имеют место отношения 
. Данные отношения в дробных числах заменим отношениями целых чисел:
2. Зная, что х содержит 30 равных частей, х2 – 20, х3 – 12, х4 –15, найдем, сколько частей содержится в их сумме:
30 + 20 + 12+ 15 = 77 (ч.).
3. Сколько рублей приходится на одну часть?
1 925 000 : 77 = 25 000 (р.).
4. Каков доход фермы в первом месяце?
25 000 • 30 = 750 000 (р.).
5. Каков доход фермы во втором месяце?
25 000 • 20 = 500 000 (р.).
6. Каков доход фермы в третьем месяце?
25 000– 12 = 300 000 (р.).
7. Каков доход фермы в четвертом месяце?
25 000– 15 = 375 000 (р.).
Ответ: в первом месяце доход фермы составил 750 000 р., во втором – 500 000 р., в третьем – 300 000 р., в четвертом – 375 000 р.
3) Задачи на деление числа на части, когда даны отдельные отношения для каждой пары искомых чисел
К задачам этого типа относят те задачи, в которых число А (значение некоторой величины) нужно разделить на части х1, х2, х3, . х„, когда дан ряд отношений для искомых чисел, взятых попарно. Алгебраическая модель:
Ввиду громоздкости формул для решения задачи в общем виде рассмотрим частный случай, когда п = 4. Алгебраическая модель:
или
Пример.В трех городах 168 000 жителей. Числа жителей первого и второго городов находятся в отношении 
, а второго и третьего городов – в отношении 
. Сколько жителей в каждом городе?
Решение. Обозначим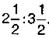 
искомые численности жителей соответственно через х1, х2, х3. Тогда кратко задачу можно записать так, как показано на рисунке 9.
Для определения численности жителей даны числа жителей в трех городах, то есть сумма трех искомых чисел, а также отдельные отношения между искомыми числами. Заменив эти отношения рядом отношений, выразим численности жителей трех городов в равных частях. Зная число частей, приходящихся на каждое из искомых чисел, найдем число частей, заключающихся в их сумме. По данной общей численности жителей в трех городах, то есть по сумме искомых чисел и по числу частей, содержащихся в этой сумме, узнаем величину одной части, а потом искомые численности жителей.
Запишем решение по действиям с пояснениями.
1. Заменяем отношение дробных чисел отношением целых чисел:
Числу жителей второго города ставим в соответствие число 15 (наименьшее общее кратное чисел 3 и 5).
Изменяем соответствующим образом получившиеся отношения:
Из отдельных отношений составляем ряд отношений:
2. 20 + 15 + 21 = 56 (ч.) – стольким равным частям соответствует число 168 000;
3. 168 000 : 56 = 3 000 (ж.) – приходится на одну часть;
4. 3 000 • 20 = 60 000 (ж.) – в первом городе;
5. 3 000 • 15 = 45 000 (ж.) – во втором городе;
6. 3 000 • 21 = 63 000 (ж.) – в третьем городе.
Ответ: 60 000 жителей; 45 000 жителей; 63 000 жителей.
4) Задачи на деление числа на части пропорционально двум, трем и так далее рядам чисел
К задачам этого типа относятся задачи, в которых число А (значение некоторой величины) нужно разделить на части х1, х2, х3. хn пропорционально двум, трем, . N рядам чисел.
Ввиду громоздкости формул для решения задачи в общем виде рассмотрим частный случай, когда п = 3 и N = 2. Пусть х1 х2, х3 прямо пропорциональны числам а1, а2, а3 и обратно пропорциональны числам b1,b2, b3.
Значит, 
(см. пункт 1 данного параграфа),
где 
Пример.Двое рабочих получили 1 800 р. Один работал 3 дня по 8 ч., другой 6 дней по 6 ч. Сколько заработал каждый, если за 1 ч. работы они получали поровну?
Решение. Краткая запись задачи показана на рисунке 10.
Чтобы узнать, сколько получил каждый рабочий, надо знать, сколько рублей платили за 1 ч. работы и сколько часов работал каждый рабочий. Чтобы узнать, сколько рублей платили за 1 ч. работы, надо знать, сколько заплатили за всю работу (дано в условии) и сколько часов работали оба рабочих вместе. Чтобы узнать общее число часов работы, надо знать, сколько часов работал каждый, а для этого необходимо знать, сколько дней работал каждый и по сколько часов в день. Эти данные в условии имеются.
Запишем решение по действиям с пояснениями:
1) 8 × 3 = 24 (ч.) – работал первый рабочий;
2) 6 × 6 = 36 (ч.) – работал второй рабочий;
3) 24 + 36 = 60 (ч.) – работали оба рабочих вместе;
4) 1800 : 60 = 30 (р.) – получали рабочие за 1 ч работы;
5) 30 × 24 = 720 (р.) – заработал первый рабочий;
6) 30 × 36 = 1080 (р.) – заработал второй рабочий. Ответ: 720 р.; 1080 р.
5) Задачи на нахождение нескольких чисел по данным их отношениям и сумме или разности (сумме или разности некоторых из них)
Пример.На оборудование детской площадки, теплицы и спортивного зала администрацией школы было израсходовано 49 000 р. Оборудование детской площадки обошлось вдвое дешевле, чем теплицы, а теплицы – в 3 раза дешевле, чем спортивного зала и детской площадки вместе. Сколько денег было израсходовано на оборудование каждого из указанных объектов?
Решение. Краткая запись задачи показана на рисунке 11.
| На детскую площадку в 2 раза меньше, чем на теплицу. |  49 000 р. |
| На теплицу в 3 раза меньше, чем на детскую площадку и спортивный зал вместе. | |
| Сколько денег израсходовано на оборудование каждого объекта? |
Рис. 11
Чтобы узнать количество денег, израсходованных на оборудование каждого объекта, надо знать, сколько частей всех израсходованных денег приходилось на оборудование каждого объекта и сколько рублей приходилось на каждую часть. Число частей израсходованных денег на оборудование каждого объекта определяется из условия задачи. Определив число частей на оборудование каждого объекта в отдельности, а затем найдя их сумму, вычислим величину одной части (в рублях).
Запишем решение по действиям с пояснениями.
1. Принимаем за 1 часть количество денег, израсходованных на оборудование детской площадки. По условию на оборудование теплицы израсходовано в 2 раза больше, то есть 1 × 2 = 2 (ч.); на оборудование детской площадки и спортивного зала вместе израсходовано в 3 раза больше, чем на теплицу, то есть 2 × 3 = 6 (ч.), следовательно, на оборудование спортивного зала израсходовали 6 – 1 = 5 (ч.).
2. На оборудование детской площадки израсходована 1 часть, теплицы – 2 части, спортивного зала – 5 частей. Весь расход составлял 1 + 2 + + 5 = 8 (ч.).
3. 8 частей составляют 49 000 р., одна часть меньше этой суммы в 8 раз: 49 000 : 8 = 6 125 (р.). Следовательно, на оборудование детской площадки израсходовали 6 125 р.
4. На оборудование теплицы израсходовано в 2 раза больше: 6 125 × 2 = 12 250 (р.).
5. На оборудование спортивного зала израсходовано 5 частей: 6 125 × 5 = 30 625 (р.).
Ответ: 6 125 р.; 12 250 р.; 30 625 р.
6) Задачи на исключение одного из неизвестных
К задачам этой группы относятся задачи, в которых даны суммы двух произведений, имеющих два повторяющихся сомножителя, и требуется найти значения этих сомножителей. Алгебраическая модель
Ответ находится по формулам:
Эти задачи решаются способом уравнивания данных, способом уравнивания данных и искомых, способом замены данных, а также так называемым способом «на предположение».
Пример.На швейной фабрике на 24 пальто и 45 костюмов израсходовали 204 м ткани, а на 24 пальто и 30 костюмов – 162 м. Сколько ткани расходуется на один костюм и сколько – на одно пальто?
Решение. Решим задачу способом уравнивания данных. Краткая запись задачи:
24 пальто и 45 костюмов – 204 м,
24 пальто и 30 костюмов – 162 м.
Сколько м ткани расходуется на одно пальто и на один костюм?
В условии задачи даны две партии ткани. В первой партии 204 м, во второй – 162 м. Ткани во второй партии меньше, потому что меньше сшито костюмов. Число пальто в первом и во втором случае одинаково. Очевидно, лишние 42 м ткани (204 – 162) в первой партии пошли на пошив 15 лишних костюмов (45 – 30). Зная, что 42 м идет на пошив 15 костюмов, можно узнать, сколько метров ткани идет на 1 костюм. Чтобы узнать, сколько метров идет на пальто, надо знать, сколько метров идет на все 24 пальто. В условии дано, что 162 м идет на 24 пальто и на 30 костюмов, но мы уже знаем, сколько метров идет на 1 костюм, следовательно, можем подсчитать, сколько метров пойдет на 30 костюмов, а потом узнаем, сколько ткани израсходовано на 24 пальто. Зная, сколько метров идет на 24 пальто, определим, сколько метров идет на 1 пальто.
Запишем решение по действиям с пояснениями:
1) 204 – 162 = 42 (м) = 4 200 (см) – на столько метров больше израсходовано ткани в первый раз;
2) 45 – 30 = 15 (к.) – столько лишних костюмов сшито в первый раз;
3) 4200 : 15 = 280 (см) – ткани идет на 1 костюм;
4) 280 × 30 = 8 400 (см) – ткани идет на 30 костюмов;
5) 16 200 – 8 400 = 7 800 (см) – ткани идет на 24 пальто;
6) 7 800 : 24 = 325 (см) – ткани идет на 1 пальто.
7) Ответ: 2 м 80 см расходуется на пошив 1 костюма; 3 м 25 см расходуется на пошив 1 пальто.
Пример.За 14 кубометров березовых и 6 кубометров сосновых дров уплачено 3760 р. В другой раз при тех же ценах за 37 кубометров березовых и 18 кубометров сосновых дров уплачено 10280 р. Сколько стоит кубометр тех и других дров?
Решение. Решим задачу способом уравнивания данных и искомых.
Краткая запись задачи (а):
а) 14 м 3 березовые и 6 м 3 сосновые – 3760 р.,
37 м 3 березовые и 18 м 3 сосновые – 10280 р.,
Сколько стоит 1 м 3 тех и других видов?
В условии задачи даны две покупки. Второй раз уплачено больше, потому что больше куплено березовых и сосновых дров. Надо изменить условие задачи так, чтобы количество каких-нибудь дров в обеих покупках было одинаково. Тогда разница в стоимости будет зависеть только от разницы в количестве одного какого-нибудь сорта дров. В данной задаче легко выравнять количество сосновых дров, увеличив в первой покупке все данные в 3 раза. Умножаем на 3 все числовые данные первой строчки: 14 × 3 = 42 (м 3 );
6 × 3 = 18 (м 3 ); 3 760 × 3 = 11280 р. Получили задачу, краткая запись которой показана (б):
б) 42 м 3 березовые и 18 м 3 сосновые – 11280 р.,
37 м 3 березовые и 18 м 3 сосновые – 10280 р.,
Сколько стоит 1 м 3 тех и других дров?
Дальше задача решается так же, как и предыдущая: на исключение неизвестных при помощи вычитания.
Запишем решение по действиям с пояснениями:
1) 18 : 6 = 3 (раз) – во столько раз во второй покупке сосновых дров больше, чем в первой;
2) 14 × 3 = 42 (м 3 ) – купили бы березовых дров в первый раз;
3) 6 × 3 = 18 (м 3 ) – купили бы сосновых дров в первый раз;
4) 3760 × 3 = 11 280 (р.) – заплатили бы за первую покупку;
5) 11280 – 10280 = 1 000 (р.) – на столько рублей заплатили бы больше за первую покупку, чем за вторую;
6) 42 – 37 = 5 (м 3 ) – купили бы березовых дров больше в первый раз, чем во второй;
7) 1 000 : 5 = 200 (р.) – стоит 1 кубометр березовых дров;
8) 200 × 37 = 7400 (р.) – стоят 37 кубометров березовых дров;
9) 10280 – 7400 = 2880(р.) – стоят 18 кубометров сосновых дров;
10) 2 880 : 18 = 160 (р.) – стоит 1 кубометр сосновых дров.
Ответ: 200 р.; 160 р.
Пример.В 12 одинаковых мешках и 9 одинаковых ящиках хранится 645 кг моркови. В мешке вмещается моркови на 10 кг больше, чем в ящике. Сколько моркови хранится в одном мешке и одном ящике?
Решение. Решим задачу способом замены данных. Графическая модель задачи представлена на рисунке 12.
По условию задачи мешок вмещает на 10 кг моркови больше, чем ящик. Следовательно, если мы будем знать, сколько килограммов моркови вмещает ящик, то легко найдем, сколько килограммов моркови вмещает мешок. 645 кг моркови хранятся в мешках и ящиках. Каждый мешок вмещает моркови на 10 кг больше, чем ящик. При замене одного мешка ящиком масса хранящейся моркови становится меньше на 10 кг. Таким образом, если бы вместо 12 мешков взяли 12 ящиков, то масса хранящейся моркови стала бы меньше на 10 × 12 кг.
Дальше можно узнать, сколько весила бы вся морковь, если бы вместо 12 мешков взяли 12 ящиков. Зная число ящиков (9 +12 = 21) и их вместимость, можно узнать, сколько килограммов моркови вмещает один ящик; а зная, сколько килограммов моркови вмещает ящик, найдем, сколько килограммов моркови вмещает мешок.
Запишем решение по действиям с пояснениями:
1. 10 × 12 = 120 (кг) – на столько килограммов моркови хранится меньше в 12 ящиках, чем в 12 мешках;
2. 645 – 120 = 525 (кг) – столько весила бы вся морковь, если бы вместо 12 мешков взяли 12 ящиков;
3. 12 + 9 = 21 (ящ.) – было бы взято ящиков;
4. 525 : 21 = 25 (кг) – моркови вмещает один ящик;
5. 25 + 10 кг = 35 (кг) – моркови вмещает один мешок.
Ответ: 35 кг, 25 кг.
Примечание. Мы заменили мешки ящиками. Можно заменить ящики мешками. Тогда масса всей хранящейся моркови будет больше на 10 × 9 кг. План и решение задачи будут аналогичны вышеприведенным.
Пример.С двух участков общей площадью в 51 га собрано 2 221 т картофеля. С каждого гектара одного участка собирали по 486 ц, а с каждого гектара второго участка собирали по 325 ц картофеля. Определите площадь каждого участка.
Решение. Решим задачу способом «на предположение». Краткая запись задачи представлена на рисунке 13.
1-й уч.– по 486 ц с 1га 2-й уч. – по 325 ц с 1 гa   Определите площадь каждого участка. |
Предположим, что с каждого гектара второго участка собирали столько же картофеля, сколько и с первого, то есть по 486 ц, тогда с 51 га было бы собрано 486 × 51 ц. На самом деле картофеля собрано меньше: (486 × 51 – 22 210) ц, потому что с каждого гектара второго участка собирали не 486 ц, а 325 ц, то есть на 161 ц меньше. Очевидно, сколько раз 161 ц содержится в (486 × 51 – 22210) ц, столько гектаров и было во втором участке. Запишем решение по действиям с пояснениями:
1) 486 × 51 = 24 786 (ц) – был бы урожай картофеля с обоих участков, если бы с каждого гектара второго участка собирали столько же, сколько и с первого, то есть по 486 ц;
2) 24 786 – 22 210 = 2 576 (ц) – разница между предполагаемым урожаем и действительным урожаем;
3) 486 – 325 = 161 (ц) – на столько центнеров с каждого гектара второго участка собирали картофеля меньше, чем с одного гектара первого участка;
4) 2 576 : 161 = 16 раз (га) – площадь второго участка;
5) 51 – 16 = 35 (га) – площадь первого участка.
Проверка. Подсчитываем урожай с каждого участка отдельно, а потом весь урожай с обоих участков. Должно получиться 2 221 т. Задачу можно решить, предполагая, что с каждого гектара обоих участков собирали по 325 ц. Составление плана решения и само решение задачи по существу будут те же.
Ответ: 35 га; 16 га.
4. Нахождение процентов (части) от данного числа
К задачам этого вида относятся задачи, в которых требуется найти р процентов (т/п часть) от числа А. Алгебраическая модель:
Пример.В телевизионной игре некто выиграл 12 000 р. Две пятых этой суммы он истратил на покупку бытовой техники, четвертую часть положил в банк, остальные деньги потратил на турпоездку с семьей во время летнего отпуска. Сколько стоила эта поездка?
Решение. Краткая запись задачи показана на рисунке 14.
Чтобы ответить на вопрос задачи, надо знать: 1) весь выигрыш; 2) деньги, израсходованные на бытовую технику; 3) деньги, положенные в банк.
| 2/5 – |  покупка бытовой техники техники; | |
| 1/4 – | в банк; | 12 000 р. |
| остальные – турпоездка. Сколько стоила поездка? |
Весь выигрыш известен из условия задачи, остальные величины надо определить. На бытовую технику израсходовано 2/5 части выигрыша. Можно начать решение задачи с определения этой части выигрыша (все данные имеются). Затем надо определить количество денег, положенных в банк: 1/4 выигрыша. Чтобы найти искомую стоимость, надо из общего количества денег вычесть деньги, затраченные на покупку бытовой техники, и деньги, положенные в банк.
Запишем решение задачи по действиям с пояснениями:
1. (12 000 : 5) × 2 = 4 800 (р.) – израсходовано на покупку бытовой техники;
2. 12 000 : 4 = 3 000 (р.) – положено в банк;
3. 4 800 + 3 000 = 7 800 (р.) – израсходовано на покупку бытовой техники и положено в банк;
4. 12 000 – 7 800 = 4 200 (р.) – осталось на турпоездку.
Ответ: поездка стоила 4 200 р.
Пример.Совхоз имеет 1 400 га земли; 32% ее занято рожью, 35% – пшеницей, 22% – овсом, остальное – клевером.
Сколько гектаров земли под рожью, пшеницей, овсом и клевером отдельно?
Решение. Краткая запись задачи:
Пшеница – 35% 1400 га
Сколько гектаров занято каждой культурой?
Площадь всего участка составляет 100%. Чтобы узнать, сколько гектаров занято каждой культурой, надо знать, сколько процентов площади занято каждой культурой и сколько гектаров приходится на 1%. Сначала найдем 1% от 1 400 га. Затем находим, сколько гектаров занято каждой культурой.
Оформим решение задачи по действиям с записью пояснений в вопросительной форме.
1. Сколько гектаров составляет 1 % всей земли?
1 400: 100 = 14 (га).
2. Сколько гектаров земли занято рожью?
3. Сколько гектаров занято пшеницей?
4. Сколько гектаров занято овсом?
5. Сколько всего гектаров занято рожью, пшеницей и овсом?
448 + 490 + 308 = 1 246 (га).
6. Сколько гектаров земли занято клевером?
1400 – 1 246 = 154 (га).
Задачу можно проверить, решив ее другим способом. Первые четыре вопроса и четыре действия остаются те же.
5. Сколько процентов земли занято рожью, пшеницей и овсом?
6. Сколько процентов земли занято клевером?
7. Сколько гектаров земли занято клевером?
Ответ: рожью занято 448 гектаров, пшеницей – 490 гектаров, овсом – 308 гектаров, клевером – 154 гектара.
Нахождение числа по данной величине его процента (части)
К задачам этого вида относятся задачи, в которых требуется найти число, если р процентов (т/п часть) его составляют а.
или 
Пример.Молоко пропускали через сепаратор и из полученных сливок сбивали масло. Масса масла, сбитого из сливок, составляет 16% массы сливок, а все сливки – 20% массы молока. Сколько литров молока нужно взять, чтобы получить 73 кг 800 г масла, если 1 л молока весит 1 025 г?
Решение. Краткая запись задачи:
Масла 73 кг 800 г;
Масло составляет 16% массы сливок; Сливки составляют 20 % массы молока;
1 л молока весит 1025 г.
Сколько литров молока надо взять?
73 кг 800 г масла получили из сливок. Масса масла составляет 16% массы сливок, а масса сливок равна 100%. По массе масла определим массу сливок, из которых сбито масло. Масса сливок, в свою очередь, составляет 20% массы молока, а масса молока равна 100%. Зная массу сливок, определим массу молока, из которого приготовлено 73 кг 800 г масла. Зная массу1 л молока и массу всего молока, найдем, сколько литров молока надо взять для приготовления 73 кг 800 г масла, то есть ответим на вопрос задачи. Оформим решение по действиям с записью пояснений в вопросительной форме.
1. Сколько весят сливки, необходимые для приготовления 73 кг 800 г масла?
73 кг 800 г = 73800 (г).
(73800 : 16) × 100 = 461250 (г).
2. Сколько весит молоко?
(461250 : 20) × 100 = 2306 250 (г).
3. Сколько литров молока нужно взять?
2306250 : 1025 = 2250 (л).
Ответ: требуется взять 2 250 л молока.
Пример.Из имеющихся денег 
израсходовали на покупку продуктов, 
– на билеты в театр, на остальные деньги купили газеты и 4 журнала. Продукты стоили на 
р. дороже газет и журналов. Сколько было денег и сколько стоили продукты?
Решение. Краткая запись задачи:
Продукты – 1/3 всего заработка;
Билеты – 2/5 всего заработка;
Газеты и журналы – остальное;
Продукты дороже газет и журналов на 
р.
Сколько было денег и сколько стоили продукты?
Все деньги представляют собой сумму трех слагаемых: часть имеющихся денег израсходована на продукты, часть – на билеты и остальная часть – на газеты и журналы. Первые два слагаемых известны, третье неизвестно. Но оно составляет разность между всеми деньгами и суммой этих слагаемых. Зная части имеющихся денег, израсходованных на продукты, газеты и журналы, найдем разность между ними в частях всех денег, которая в то же время равна р. По данной величине дроби найдем всю сумму, то есть получим ответ на первый вопрос задачи. Зная всю сумму, найдем ее часть, израсходованную на продукты, то есть получим ответ на второй вопрос задачи.
Оформим решение по действиям с записью пояснений в вопросительной форме.
1. Какая часть денег израсходована на продукты и билеты в театр?
2. Какая часть денег израсходована на газеты и журналы?
3. На какую часть денег расход на продукты больше расхода на газеты и журналы?
4. Какова вся сумма денег?
5. Сколько стоят продукты?
Ответ: всего было 117 р.; продукты стоили 39 р.
Нахождение процентного отношения двух чисел
Кзадачам этого вида относятся задачи, в которых требуется определить, сколько процентов составляет число В от числа А. Алгебраическая модель:
Примечание. Задачи этой группы могут рассматриваться как задачи на пропорциональные величины и поэтому могут решаться всеми способами решения задач на простое тройное правило.
Пример.В школе обучается 320 мальчиков и 350 девочек. На занятиях присутствуют 304 мальчика и 336 девочек. Сколько присутствует в школе (в процентах): а) мальчиков; б) девочек; в) всех учащихся? г) сколько процентов составляет число отсутствующих учащихся от числа присутствующих?
1) 
– мальчиков присутствует в школе;
2) 
– девочек присутствует в школе;
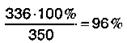
3) 320 + 350 = 670 (уч.) – всего учащихся в школе;
4) 304 + 336 = 640 (уч.)– присутствуют в школе;
5) 
– всех учащихся присутствует в школе;
6) 670 – 640 = 30 (уч.) – отсутствуют в школе;
Источник
