Решение уравнений способом группировки это

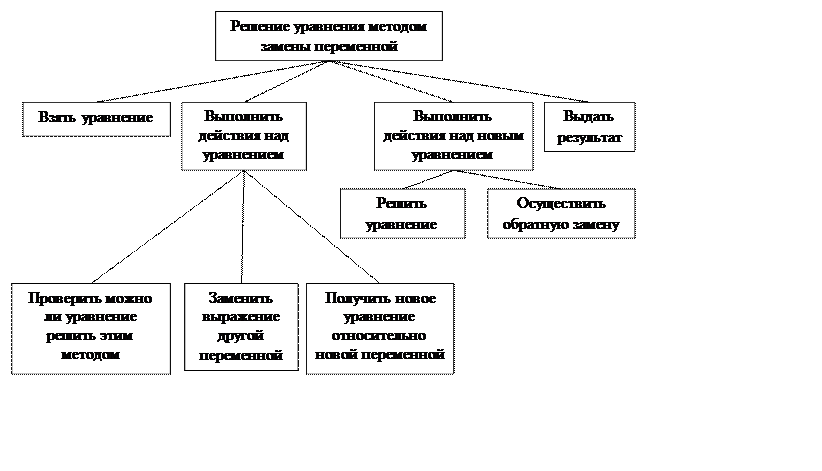
Решение уравнения методами группировки и замены переменной

Страницы работы

Содержание работы

Лабораторная работа №1

Цель работы: Решить уравнения методами:

б) замены переменной.

Теоретическая часть работы

Способ группировки разложение на множители

Для того, чтобы разложить многочлен 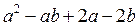на множители:

1 – Объединим слагаемые попарно в группы (говорят «сгруппируем слагаемые»): два в одну группу, и два — в другую .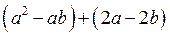

2 – В каждой паре вынесем за скобки общий множитель.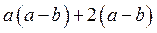

3 – Заметим, что оба полученных слагаемых также имеют общий множитель, который можно вынести за скобки .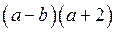

Не любая группировка приводит к разложению на множители. В случае неудачи попробуйте сгруппировать по-другому, или вообще попытайтесь применить другой метод.

Рассмотрим решение уравнения способом разложения на множители на конкретном примере:

Применив способ группировки, получим:

Помня, что произведение равно 0 в случае, если один из множителей равен 0, получим корни уравнения:

Метод введения новой переменной

Пример.

.

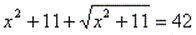
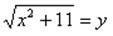
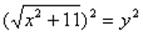
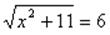
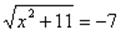
Введем новую переменную , учитывая, что , получаем квадратное уравнение у 2 +у – 42=0 , корни которого -7 и 6. Возвращаясь к переменной х, получаем уравнения и , последнее не имеет корней, т.к. арифметический квадратный корень – неотрицательное число, а первое уравнение можно решить, используя определение арифметического квадратного корня 6 2 = х 2 +11 , решение которого х=5 и х=-5.

Если уравнение можно свести к уравнению, содержащему два или несколько одинаковых выражений, то это уравнение можно решить методом замены переменной. Для этого заменяют такое выражение другой переменной, получают новое уравнение относительно новой переменной, решают его, затем осуществляют обратную замену, возвращаясь к прежней переменной.

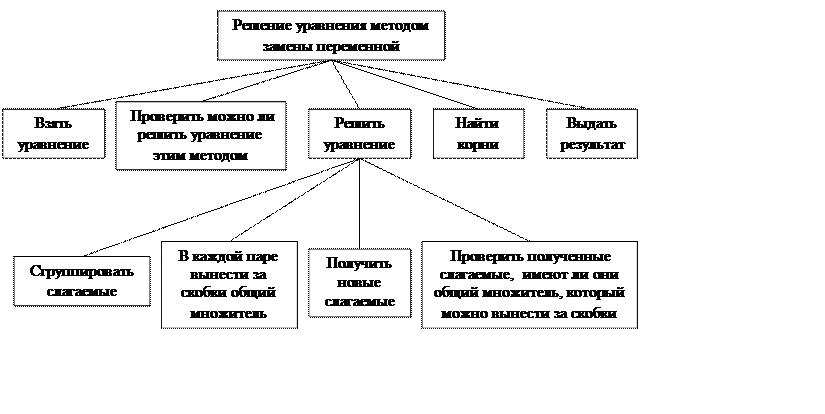
Структурная схема программы: а) способ группировки разложение на множители

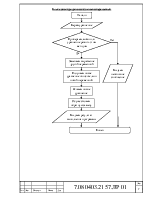
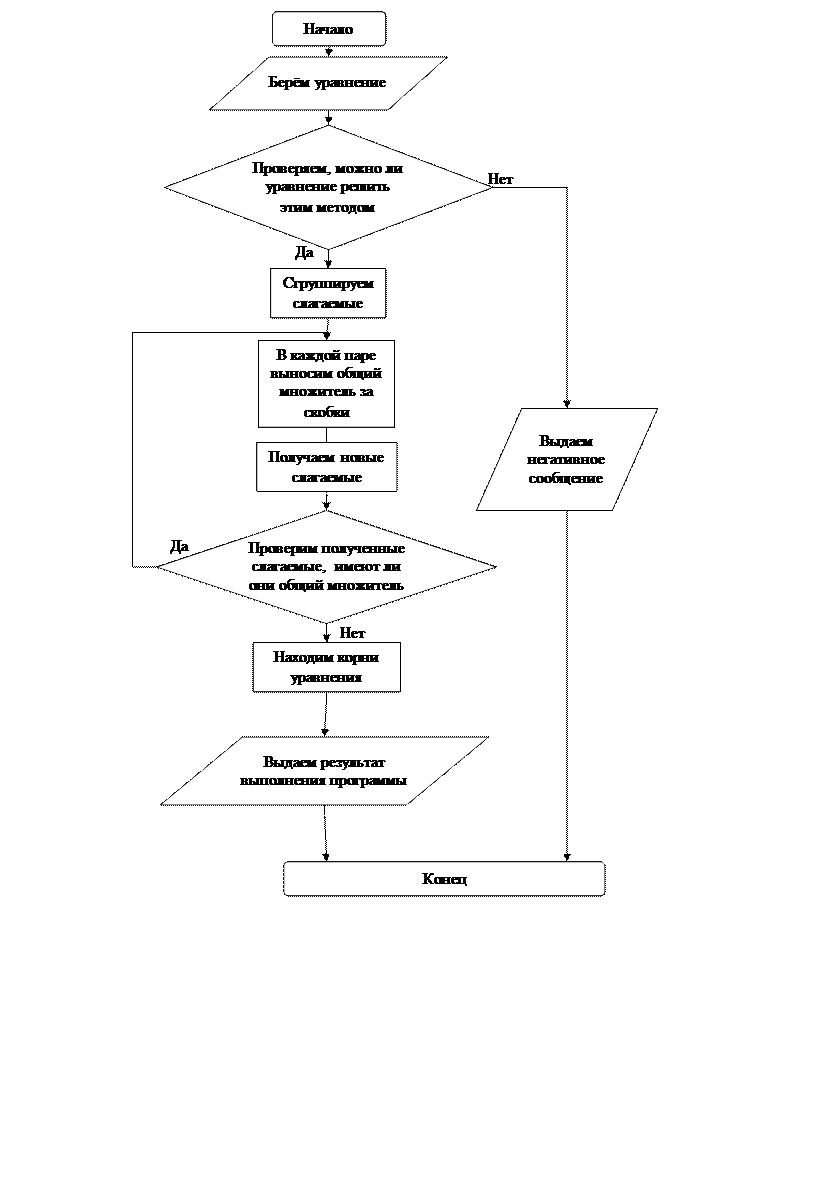
Блок-схема программы: а) способ группировки разложение на множители

Структурная схема программы: б) замены переменной

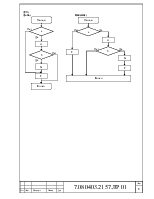
Блок-схема программы: б) замены переменной

Источник

Способ группировки

Кроме вынесения общего множителя за скобки существует еще один способ разложения многочлена на множители — способ группировки.

Этот способ разложения на множители считается более сложным, поэтому перед его изучением, убедитесь, что вы уверенно выносите общий множитель за скобки.

Чтобы разложить многочлен на множители способом группировки, необходимо сделать следующее.

1. Подчеркнуть повторяющиеся буквы и записать друг за другом одночлены с одинаковыми буквенными множителями.
2. Вынести общий множитель за скобки у каждой группы одночленов.
3. Вынести полученный общий многочлен за скобки.

Рассмотрим пример разложения многочлена на множители способом группировки.

Подчеркнем повторяющиеся буквенные множители в одночленах.

Примеры способа группировки

Группировать одночлены можно по-разному. При правильной группировке должен появиться общий многочлен .

Рассмотрим пример. Требуется разложить многочлен на множители, используя способ группировки.

Первый способ

Обратим внимание, что в двух одночленах повторяется « y 2 » и « z 2 ». Подчеркнем повторяющиеся одночлены и запишем их друг за другом. Затем вынесем общий множитель у каждой группы одночленов.

48x z 2 + 32x y 2 − 15 z 2 − 10 y 2 = 48x z 2 − 15 z 2 + 32x y 2 − 10 y 2 = 3z 2 (16x − 5) + 2y 2 (16x − 5) =
= (16x − 5)(3z 2 + 2y 2 )

Второй способ

Запишем пример еще раз. Теперь обратим внимание, что в первых двух одночленах повторяется « x ». Подчеркнем повторяющиеся одночлены. Вынесем общий множитель у каждой группы одночленов.

48 x z 2 + 32 x y 2 − 15z 2 − 10y 2 = 16x(3z 2 + 2y 2 ) − 5(3z 2 + 2y 2 ) = (3z 2 + 2y 2 )(16x − 5)

В итоге получился такой же ответ, как и при первом способе.

Рассмотрим еще один пример разложения многочлена способом группировки.

4q(p − 1) + p − 1 = 4q(p − 1) + (p − 1) = 4q(p − 1) + 1 · (p − 1) = (p − 1)(4q + 1)
В этом примере следует отметить, что для вынесения общего многочлена мы добавили умножение на 1 к многочлену (p − 1) , что не изменяет результат умножения.
Это помогает понять, что останется во второй скобке после вынесения общего многочлена.

Смена знаков в скобках

Иногда для вынесения общего многочлена требуется сменить все знаки одночленов в скобках на противоположные.

Для этого за скобки выносится знак « − », а в скобках у всех одночленов меняются знаки на противоположные.

2ab 2 − 3x + 1 = −( − 2ab 2 + 3x − 1)

Рассмотрим пример способа группировки, где для вынесения общего многочлена, нам потрубуется выполнить смену знаков в скобках.

• 2m(m − n) + n − m = − 2m( − m + n) + (n − m) = −2m(n − m) + 1 · (n − m) =
  = (n − m)(−2m + 1)

Источник

Разложение многочлена способом группировки

О чем эта статья:

Основные понятия

Мы знаем, что слово «множитель» происходит от слова «умножать».

Возьмем, например, число 12. Чтобы разложить его на множители, нужно написать его по-другому, а именно в виде «произведения» множителей.

Число 12 можно получить, если умножить 2 на 6. А 6 можно представить, как произведение 2 и 3. Вот так:

Так выглядит пошаговое разложение на множители. Числа, которые подчеркнуты на картинке — это множители, которые дальше разложить уже нельзя.

Разложение многочлена на множители — это преобразование многочлена в произведение, которое равно данному многочлену.

5 способов разложения многочлена на множители

1. Вынесение общего множителя за скобки.
2. Формулы сокращенного умножения.
3. Метод группировки.
4. Выделение полного квадрата.
5. Разложение квадратного трехчлена на множители.

Способ группировки множителей

Разложение на множители методом группировки возможно, когда многочлены не имеют общего множителя для всех членов многочлена.

Этот способ применяется в тех случаях, когда многочлен удается представить в виде пар слагаемых таким образом, чтобы из каждой пары можно было выделить один и тот же множитель. Этот общий множитель можно вынести за скобку. И тогда исходный многочлен будет представлен в виде произведения, что значительно облегчает задачу.

Разложить на множители методом группировки можно в три этапа:

1. Объединить слагаемые многочлена в группы, которые содержат общий множитель. Для наглядности их можно подчеркнуть.
2. Вынести общий множитель за скобки.
3. Полученные произведения имеют общий множитель в виде многочлена, который нужно вынести за скобки.

Объединить члены многочлена в группы можно по-разному. И ее всегда группировка может быть удачной для последующего разложения на множители. В таком случае нужно продолжить эксперимент и попробовать объединить в группы другие члены многочлена.

Чтобы понять эти сложные выражения, применим правило группировки множителей при решении примеров. Рассмотрим два способа.

Пример 1. Разложить на множители методом группировки: up — bp + ud — bd.

up — bp + ud — bd = (up — bp) + (ud — bd)

Заметим, что в первой группе повторяется p, а во второй — d.

Вынесем в первой группе общий множитель p, а во второй общий множитель d.

Получим: p(u — b) + d(u — b).

Заметим, что общий множитель (u — b).

Вынесем его за скобки:

Группировка множителей выполнена.

up — bp + ud — bd = (up + ud) — (bp + bd)

Заметим, что в первой группе повторяется u, а во второй — b.

Вынесем в первой группе общий множитель u, а во второй общий множитель b.

Получим: u(p + d) — b(p + d).

Заметим, что общий множитель (p + d).

Вынесем его за скобки:

Группировка множителей выполнена.

От перестановки мест слагаемых сумма не меняется, поэтому оба ответа верны:

(u — b)(p + d) = (p + d)(u — b).

Вот так работает алгоритм разложения многочлена на множители способом группировки. Продолжим практиковаться на примерах.

Пример 2. Разложить на множители выражение: c(m — n) + d(m — n).

1. Найдем общий множитель: (m — n)
2. Вынесем общий множитель за скобки: (m — n)(c + d).

Ответ: c(m — n) + d(m — n) = (m — n)(c + d).

Пример 3. Разложить на множители с помощью группировки: 5x — 12z (x — y) — 5y.

5x — 12z (x — y) — 5y = 5x — 5y — 12z (x — y) = 5(x — y) — 12z (x — y) = (x — y) (5 — 12z)

Ответ: 5x — 12z (x — y) — 5y = (x — y) (5 — 12z).

Иногда для вынесения общего многочлена нужно заменить все знаки одночленов в скобках на противоположные. Для этого за скобки выносится знак минус, а в скобках у всех одночленов меняем знаки на противоположные.

Проверим как это на следующем примере.

Пример 4. Произвести разложение многочлена на множители способом группировки: ax 2 — bx 2 + bx — ax + a — b.

1. Сгруппируем слагаемые по два и вынесем в каждой паре общий множитель за скобку:

ax 2 — bx 2 + bx — ax + a — b = (ax 2 — bx 2 ) + (bx — ax) + (a — b) = x 2 (a — b) — x(a — b) + (a — b)

Получили три слагаемых, в каждом из которых есть общий множитель (a — b).

1. Теперь вынесем за скобку (a — b), используя распределительный закон умножения:

x 2 (a — b) + x(b — a) + (a — b) = (a — b)(x 2 + x + 1)

Ответ: ax 2 — bx 2 + bx — ax + a — b = (a — b)(x 2 + x + 1)

Источник

Презентация по алгебре»способ группировки»

Выбранный для просмотра документ Приложение 1.ppt

Описание презентации по отдельным слайдам:

Учитель математики Наталья Игоревна Касьянова МБОУ гимназия №5 г. Морозовск Ростовской обл.

УСТНО Что значит разложить многочлен на множители? Какие способы разложения многочлена на множители вы знаете? Сформулируйте алгоритм разложения многочлена на множители способом вынесения общего множителя за скобки.

УСТНО Вынести за скобки общий множитель: 1) 6а+9х; 2) ay–ax; 3) a2 –a³b; 4) 16mn – 4mn3 ; 5) 12(a+b) –x(a+b).

«Вынесение общего множителя за скобки»

Вынеси общий множитель за скобки: 15х + 10y; a2 – ab; n(7-m) + k(7–m); 8m2n – 4mn3 ; a(b-c)+3(c-b). 9n + 6m; b² — ab; b(a+5) – c(a+5); 20x³y² + 4x²y³; 6(m-n)+s(n-m).

ПРОВЕРКА 5(3х +2у); a(a-b); (7-m)(n+k); 4mn(2m-n²); (b-c)(a+3). 3(3n + 2m); b(b – a); (a+5)(b-c); 4xy(5x + y); (6–s)(m-n). 5 – «5»; 4 – «4»; 3 – «3».

РЕШИТЕ УРАВНЕНИЕ 1) x (x-11) = 0; 2) 6x² – 2x = 0; 3) x2 + 3x + 6 + 2x = 0. — Есть ли общий множитель у всех слагаемых? — Значит способ разложения на множители не подходит.

x2 + 3x + 6 + 2x = 0. РЕШЕНИЕ: Пристально посмотрим на левую часть уравнения…Что-нибудь вы видите? Попробуем объединить в группы: (x2 + 3x) + (6 + 2x) = 0; Теперь у одночленов в скобках появились общие множители х(x + 3) + 2(3 + x) = 0; (х + 3)(х +2) = 0;

Способ группировки Данный способ применяют к многочленам, которые не имеют общего множителя для всех членов многочлена. Чтобы разложить многочлен на множители способом группировки, нужно: Объединить члены многочлена в такие группы, которые имеют общий множитель в виде многочлена. Вынести этот общий множитель за скобки.

ПРИМЕР Разложить на множители многочлен: xy-6+3х-2y Первый способ группировки: xy-6+3х-2y=(xy-6)+(3x-2y).(Группировка неудачна.) Второй способ группировки: xy-6+3х-2y=(xy+3x)+(-6-2y)= =x(y+3)-2(y+3)=(y+3)(x-2). Третий способ группировки: xy-6+3х-2y=(xy-2y)+(-6+3x)= =y(x-2)+3(x-2)=(x-2)(y+3). Ответ: xy-6+3х-2y=(x-2)(y+3). Как видите, не всегда с первого раза группировка оказывается удачной. Если группировка оказалась неудачной, откажитесь от нее и ищите иной способ.

РАЗЛОЖИТЕ НА МНОЖИТЕЛИ: ах + 3х + 4а + 12; аb — 8а – bх + 8х; x2m — x2n + y2m — y2n.

Дифференцированные задания по уровням А. Задания нормативного уровня. 1) 7а — 7в + аn – bn 2) xy + 2y + 2x + 4 3) y2a — y2b + x2a — x2b Б. Задания компетентного уровня 1) xy + 2y — 2x – 4 2) 2сх – су – 6х + 3у 3) х2 + xy + xy2 + y3 С. Задания творческого уровня 1) x4 + x3y — xy3 — y4 2) ху2 – ву2 – ах + ав + у2 – а 3) х2 – 5х + 6

ДОМАШНЕЕ ЗАДАНИЕ § 32 (алгоритм знать); № 32.3(а); № 32.4 (а).

ИТОГ УРОКА а) С каким новым способом разложения многочлена на множители вы познакомились сегодня? б) В чем он заключается? в) К каким многочленам обычно применяют способ группировки?

БЛАГОДАРЮ ЗА УРОК!

Выбранный для просмотра документ Статья.docx

ТЕМА: РАЗЛОЖЕНИЕ МНОГОЧЛЕНА НА МНОЖИТЕЛИ СПОСОБОМ ГРУППИРОВКИ.

Тема «Разложение многочленов на множители» имеет большое значение и занимает значительное место в курсе алгебры 7 класса.

Во-первых, учащимся учитель объясняет, как с помощью разложения многочлена на множители можно упростить запись многочлена или облегчить вычисление числового значения выражения.

Во-вторых, в дальнейшем разложение на множители будет использоваться на протяжении всего курса алгебры: при выполнении действий над алгебраическими дробями — сокращении, сложении и вычитании, умножении и делении, а также при решении уравнений и неравенств и др.

Задача о разложении многочлена на множители является достаточно сложной. Это можно объяснить отсутствием четкого алгоритма разложения многочленов на множители, часто приходится догадываться, какой из способов разложения можно применить в каждом конкретном случае. Учитывая эти факты, становится ясно, насколько серьезная задача стоит перед учителем: сформировать у всех учащихся (включая учащихся со специальными потребностями) навыки в разложении на множители сначала на простых упражнениях, а для сильных учащихся на протяжении всего года и далее до конца курса рассмотреть более сложные случаи.

Основные характеристики урока:

Урок алгебры в 7 классе.

Технологии обучения: личностно – ориентированная, информационно – коммуникационная, проблемного обучения.

Продолжительность: 45 минут.

Автор: Касьянова Наталья Игоревна, учитель математики, МБОУ гимназия №5, г. Морозовск, Ростовская область.

При изучении темы «Разложение многочлена на множители способом группировки» ставятся следующие цели:

1) выработать у учащихся умения выполнять разложение многочленов на множители способом группировки,

2) выработать у учащихся умения применять полученные знания для рационализации вычислений, решения уравнений, доказательства тождеств.

1) формирование алгоритмического мышления;

2) формирование у учащихся навыков умственного труда — планирование своей работы, поиск рациональных путей ее выполнения, критическую оценку результатов;

1) эстетическое воспитание учащихся;

2) формирование представлений о математике как части общечеловеческой культуры.

Тип урока: изучение нового материала, проблемный.

Методы обучения: проблемный, частично-поисковый.

Форма организации учебной деятельности: групповая, фронтальная, индивидуальная.

Оборудование: персональный компьютер, мультимедийный проектор, экран, Презентация Power Point (Приложение 1).

Актуализация опорных знаний: ответы на устные вопросы и устные задания по теме «Вынесение общего множителя за скобки»; математический диктант с дальнейшей проверкой (слайды № 2-6).

Мотивирование необходимости разложения многочлена на множители — решение уравнений слайда № 8 и создание проблемной ситуации (уравнение № 3 не решается известным способом «вынесения общего множителя за скобки»). Постановка учебной задачи: научиться раскладывать многочлен на множители другим способом.

Совместное решение проблемы (слайд № 9), формулирование алгоритма разложения многочлена на множители способом группировки (слайд № 10) и рассмотрение примера на применение данного алгоритма несколькими способами (слайд № 11).

Применение полученных знаний при решении упражнений – работа у доски и с места (слайд № 12).

Дифференцированные задания по уровням – учащиеся выбирают один из вариантов, который соответствует их уровню знаний (слайд № 13).

Итог урока и домашнее задание (слайды № 14-16).

Список используемой литературы:

Алгебра. 7 класс. В 2 ч. Ч. 1. Учебник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – М.: Мнемозина, 2009.

Алгебра. 7 класс. В 2 ч. Ч. 2. Задачник для учащихся общеобразовательных учреждений / А. Г. Мордкович. – М.: Мнемозина, 2009.

Алгебра. 7 класс. Самостоятельные работы для учащихся общеобразовательных учреждений / Л. А. Александрова; под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.

Алгебра. 7 класс. Контрольные работы для учащихся общеобразовательных учреждений / Л. А. Александрова; под ред. А. Г. Мордковича. – М.: Мнемозина, 2009.

Источник