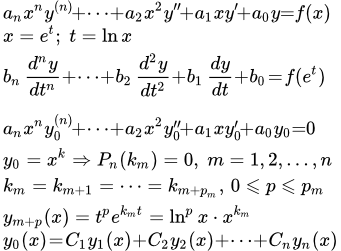Решение уравнений способом эйлера

Источник

Дифференциальное уравнение Эйлера

Напомним, что необходимым условием существования у дифференцируемой функции экстремума в некоторой точке является равенство нулю производной в этой точке: , или, что то же самое, равенство нулю дифференциала функции .

Нашей ближайшей целью будет найти аналог этого условия в вариационном исчислении и выяснить, какому необходимому требованию должна удовлетворять функция, дающая экстремум функционалу.

Мы покажем, что такая функция должна удовлетворять некоторому дифференциальному уравнению. Форма уравнения будет зависеть от вида рассматриваемого функционала. Изложение мы начнем с так называемого простейшего интеграла вариационного исчисления, под которым подразумевают функционал, имеющий следующее интегральное представление:

Функция , стоящая под знаком интеграла, зависит от трех аргументов . Будем считать ее определенной и дважды непрерывно дифференцируемой по аргументу для всех значений, по аргументам же и — в некоторой области плоскости . Ниже предполагается, что мы всегда будем находиться внутри этой области.

Под понимается некоторая функция от

непрерывно дифференцируемая на отрезке , и есть производная от нее.

Геометрически функцию можно изобразить в плоскости некоторой линией , лежащей над отрезком (рис. 3).

Интеграл (9) является обобщением интегралов (3) и (6), с которыми мы встретились в задачах о линии наискорейшего ската и поверхности вращения наименьшей площади. Значение его зависит от выбора функции или от линии , и задача о его минимуме имеет следующий смысл.

Дано некоторое множество функций (10) (линий ). Среди них нужно найти ту функцию (линию ), для которой интеграл имеет наименьшее значение.

Мы должны прежде всего точно определить множество функций, для которых мы будем рассматривать значение интеграла (9). Функции этого множества в вариационном исчислении обычно называют допустимыми к сравнению. Рассмотрим задачу с закрепленными граничными значениями. Множество допустимых функций определяется здесь двумя следующими требованиями:

1) функция непрерывно дифференцируема на отрезке ;

2) на концах отрезка функция принимает заданные наперед значения

В остальном функция может быть совершенно произвольной. Если говорить языком геометрии, мы рассматриваем всевозможные гладкие линии, лежащие над промежутком , которые проходят через две точки и и могут быть заданы уравнением (10). Функцию, доставляющую минимум интегралу, будем считать существующей и назовем ее .

Следующие простые и остроумные соображения, часто применяемые в вариационном исчислении, дают возможность весьма просто выяснить необходимое условие, которому должна удовлетворять . По сути дела они позволяют задачу о минимуме интеграла (9) привести к задаче о минимуме функции.

Рассмотрим семейство функций, зависящее от численного параметра

Чтобы функция при любом была допустимой функцией, мы должны считать непрерывно дифференцируемой и обращающейся в нуль на концах отрезка

Интеграл (9), вычисленный для , будет некоторой функцией параметра

Разность называют вариацией (изменением) функции и обозначают , а разность — полной вариацией интеграла (9). Отсюда и произошло название вариационного исчисления.

Так как функция дает минимальное значение интегралу, то функция должна иметь минимум при , и производная от нее в этой точке обязана обращаться в нуль

Последнее равенство должно выполняться при всякой непрерывно дифференцируемой функции , обращающейся в нуль на концах отрезка . Для получения вытекающего отсюда следствия удобнее второй член в условии (14) преобразовать интегрированием по частям

и придать условию (14) другую форму

Может быть доказана следующая простая лемма.

Пусть выполняются условия:

1) функция непрерывна на отрезке ;

2) функция непрерывно дифференцируема на отрезке и на концах отрезка обращается в нуль.

Если при любой такой функции интеграл равен нулю, то отсюда следует, что .

Действительно, допустим, что в некоторой точке с функция отлична от нуля, и покажем, что тогда заведомо существует такая функция , для которой , вопреки условию леммы.

Так как и непрерывна, наверное существует около точки такой промежуток , в котором будет всюду отличной от нуля и, стало быть, сохранять знак.

Всегда можно построить функцию , непрерывно дифференцируемую на , положительную на и равную нулю всюду вне (рис. 4).

Такой будет, например, , определенная равенствами

Но для такой функции

Последний же интеграл не может быть равен нулю, так как произведение внутри промежутка интегрирования отлично от нуля и сохраняет знак.

Ввиду того, что равенство (15) должно выполняться для всякой , непрерывно дифференцируемой и обращающейся в нуль на концах отрезка , мы можем, согласно лемме, утверждать, что это может быть только в том случае, когда

или после вычисления производной по переменной

Равенство это является дифференциальным уравнением 2-го порядка относительно функции . Оно называется уравнением Эйлера .

Мы можем сделать следующее заключение.

Если функция доставляет интегралу минимум, то она должна удовлетворять дифференциальному уравнению Эйлера (17). Последнее в вариационном исчислении имеет значение, вполне сходное со значением необходимого условия в теории экстремумов функций. Оно позволяет сразу отбросить все допустимые функции, которые этому условию не удовлетворяют, так как на них интеграл заведомо не может достигать минимума. Этим очень сильно сужается круг допустимых функций, подлежащих изучению. Свое внимание мы можем сосредоточить только на решениях уравнения (17).

Сами решения уравнения (17) обладают тем свойством, что производная

для них обращается в нуль при любых , и они аналогичны по своему значению стационарным точкам функции. Поэтому часто говорят, что на решениях (17) интеграл имеет стационарное значение.

В нашей задаче с закрепленными граничными значениями нужно найти далеко не все решения эйлерова уравнения, а только те из них, которые принимают предписанные значения в точках .

Обратим внимание на то, что уравнение Эйлера (17) имеет 2-й порядок. Общее его решение будет содержать две произвольные постоянные

Их нужно определить так, чтобы интегральная кривая проходила через точки и , что доставляет два уравнения для нахождения постоянных и

Во многих случаях эта система имеет только одно решение, и тогда будет существовать только одна интегральная линия, проходящая через точки и .

Разыскание функций, подозрительных на минимум интеграла, мы привели к решению следующей граничной задачи дифференциальных уравнений: на отрезке нужно найти те решения уравнения (17), которые на концах этого отрезка принимают заданные значения .

Часто эту последнюю задачу удается решить при помощи методов, известных в теории дифференциальных уравнений.

Еще раз указываем на то, что каждое решение такой граничной задачи может только подозреваться на минимум и в дальнейшем еще надлежит проверить, будет ли оно или не будет доставлять минимальное значение интегралу. Но в частных случаях, особенно часто встречающихся в приложениях, уравнение Эйлера вполне решает задачу о нахождении минимума интеграла. Пусть нам заранее будет известно, что функция, доставляющая минимум интегралу, существует, и мы допустим, кроме того, что уравнение Эйлера (17) имеет только одно решение, удовлетворяющее граничным условиям (11), и, стало быть, только одна допустимая линия может быть заподозрена на минимум. При этих условиях можно быть уверенным в том, что найденное решение уравнения (17) действительно дает минимум интегралу.

Пример . Ранее было установлено, что [url]задача о линии наискорейшего ската[/url] может быть приведена к нахождению минимума интеграла

на множестве функций, удовлетворяющих граничным условиям .

Источник