Исследовательская работа по теме: «Функционально-графический метод решения уравнений»
Понятие функциональной зависимости является одним из центральных в математике, пронизывает все ее приложения. Оно, как ни одно другое, приучает воспринимать величины в их живой изменчивости, во взаимной связи. Изучение поведения функций и построение их графиков является важным разделом школьного курса. Существуют различные способы задания функции: аналитический, табличный, графический. Иногда график является единственным возможным способом задания функции. Свободное владение техникой построения графиков часто помогает решать сложные задачи, а порой является единственным средством их решения.
Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Думаю, что знания, полученные мной в процессе работы, помогут мне при сдаче экзаменов. Мой проект поможет понять другим ученикам применение функционально-графического метода решения задач, узнать о происхождении, развитии этого метода. Материал данной работы можно рекомендовать к использованию на уроках математики или на занятиях школьного математического кружка в качестве дополнительного материала.
Скачать:
| Вложение | Размер |
|---|---|
| Презентация исследовательской работы | 341.78 КБ |
Предварительный просмотр:
Подписи к слайдам:
Подготовила: Гребеникова Софья Викторовна 10 класс Руководитель: Товменко Светлана петровна учитель математики Функционально-графический метод решения уравнений
Содержание 1.Суть функционального метода 2.Применение функционального метода при решении уравнений и неравенств 3.Решение задач из КИМ ЕГЭ по теме «Функционально-графический метод решения уравнений» 4.Заключение 5.Список литературы
Суть функционального метода В ряде случаев точное решение уравнений f (x) = g (x) по изученным правилам затруднительно и ли даже невозможно. Однако бывает достаточно обратить внимание на свойства функций f и g , как сразу решается вопрос о наличии решений уравнения или выявляется наиболее рациональный приём его решения. Основу для таких утверждений даёт нам одно из определений уравнения, как равенства двух функций. Значит , суть функционального метода: использование свойств Функций или построение графиков для решения уравнений. Выделим следующие компоненты метода:
Отыскание области определения функций Отыскание области значения функции Исследование функций на монотонность Исследование функций на чётность Соотнесение свойств функций, входящих в уравнение, с условием Построение графиков функций, входящих в уравнение Отыскание корней уравнения методом подбора Учитывая компоненты метода, выделим способы реализации: Доказательство отсутствия решения уравнения на основе использования области определения, области значения, свойств монотонности и т.д. Отыскание одного или нескольких корней уравнения с последующим доказательством Выяснение того, что область определения содержит один элемент и проверка этого значения на основании определения корня уравнения Преобразование функций, входящих в уравнение к виду, удобному для установления монотонности одной из частей уравнения (или обеих) либо оценки её множества значений Графическое решение уравнений
Применение функционального графического метода при решении уравнений Графический метод решения уравнений На практике довольно часто оказывается полезным г рафический метод решения уравнений. Он заключается В следующем: пусть нам дано уравнение вида f(x)=g(x). Мы строим два графика y=f(x) и y=g(x) на одной координатной плоскости и отмечаем точки, в которых наши графики пересекаются. Абцисса точки пересечения (координата по Х) – это и есть решение нашего уравнения.
Пример. Решить уравнение: √x+1=|x− 1| Решение. Построим графики функций, на одной координатной плоскости: y=√ x+1 и y=|x− 1| Как видно из рисунка наши графики пересекаются в двух точках с координатами: А(0;1) и B(4;3). Решением исходного уравнения будут абсциссы этих точек. Ответ: х=0 и х=4.
Функциональный метод Пример Решим уравнение х5 + 5х – 42 = 0 По виду это уравнение относится к числу тех, которые решаются методом разложения на множители. Этот метод требует значительных усилий. Представив это уравнение в виде: х5 = 42 – 5х и заметив, что функция у=х5 возрастает, а функция у=42-5х убывает, можно с делать вывод, что уравнение имеет не больше одного корня. Подбором выясняем, что этот корень х=2
Применение области определения функции Пример Решений нет Ответ
Пример Проверим, является ли корнем уравнения : ответ:х=0
Использование области значений функции Пример нет решений Ответ:
Решение уравнений и неравенств с использованием области о пределения, области значения и монотонности функции Пример Подбором находим
Решение уравнений и неравенств с использованием свойства монотонности функции Пример 1. где убывающая – убывающая, то уравнение по утверждению имеет хотя бы одно решение. Подбором выясняем
Решение задач из КИМ ЕГЭ по теме «Функционально-графический метод решения уравнений» Найти все значения p , при которых уравнение /х-2/ + /х-3/ = р имеет хотя бы один корень Решение: Построим два графика функций: у= /х-2/ + /х-3/ и у=р Для построения графика функции у= /х-2/ + /х-3/ найдем нули выражений х-2=0 и х-3=0; х1=2,х2=3. Рассмотрим, как поведёт себя функция на промежутках: 1.(- ∞; 2) 2. [2;3 3.(3 ; + ∞)
Заключение Выполнив работу, изучив теоретическую часть и изучив примеры решения уравнений, я пришла к выводу, что функциональный метод решения уравнений имеет несколько преимуществ, против других способов решения: упрощённое и ускоренное решения уравнений В современной жизни решение уравнений именно функционально-графическим методом является неотъемлемой частью выпускных и вступительных экзаменов в различные учебные заведения, поэтому очень важно понять и разобраться с этой темой ещё в школе. Для того, чтобы научиться решать уравнения функционально-графическим методом, необходимо постоянно тренироваться в их решении. В этом нелегком деле вам могут помочь различные методические пособия, задачники по элементарной математике, сборники конкурсных задач, занятия по математике в школе .
Источник
Функционально-графический метод решения уравнений
Функционально-графический метод является, пожалуй, самым красивым и наглядным из всех методов решения уравнений. Это объясняется тем, что он подразумевает использование функций, их свойств и графиков. В этой статье мы дадим краткий обзор трех основных направлений функционально-графического метода:
- Первое направление базируется на использовании графиков функций, отвечающих частям уравнения.
- Второе направление основано на использовании свойств возрастающих и убывающих функций.
- Третье направление функционально-графического метода связано с ограниченностью функций, отвечающим частям уравнения.
Материал этой статьи перекликается с информацией, приведенной в школьных учебниках, например, [1, с. 216-218]. Но здесь мы еще дополним этот материал ссылками на очень подробное описание всех направлений функционально-графического метода, включающее обоснование методов, графические иллюстрации, алгоритмы и решения характерных уравнений.
Графический метод
Решение уравнений графическим методом предполагает использование графиков функций, отвечающих частям уравнения, для определения количества корней уравнения, их приближенных, а в некоторых случаях и точных значений. Корнями уравнения являются абсциссы точек пересечения графиков соответствующих функций.
Например, графический метод позволяет определить, что уравнение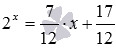 
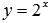
имеет два корня и указать их значения ·2 и 1 . Все это видно по чертежу, на котором в одной системе координат построены графики функций 
и 
:
С графическим методом связан ряд нюансов, касающихся сложности построения функций в общем случае, близости графиков на некоторых участках, приблизительности определяемых по графикам результатов и т.д. Все они разобраны в отдельной статье «Графический метод решения уравнений». Там же приведено обоснование метода, алгоритмы и примеры решения характерных уравнений с детальным пояснением хода решения.
Одна функция убывает, другая — возрастает
Идея этого направления функционально-графического метода решения уравнений в следующем: если на некотором числовом промежутке X одна из функций y=f(x) и y=g(x) убывает, а другая – возрастает, то на промежутке X уравнение f(x)=g(x) либо не имеет корней, либо имеет один единственный корень. Этот метод в основном применяется для обоснования вывода об отсутствии корней уравнения, который получен каким-либо методом, например, графическим, или для обоснования единственности корня, который был найден каким-либо способом, часто путем подбора.
Например, при помощи рассматриваемого метода можно решить уравнение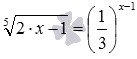 
. Его корень несложно подобрать, им является число 1 . При этом функция 
, отвечающая левой части уравнения, возрастающая, а функция 
, соответствующая правой части уравнения, убывающая. Поэтому, подобранный корень является единственным.
Решение других характерных примеров, обоснование метода, рекомендации по подбору корня и по обоснованию возрастания/убывания функций Вы найдете в этой статье.
Метод оценки
Решение уравнения методом оценки предполагает получение оценок значений выражений, отвечающих частям уравнения, с целью обосновать на их основе отсутствие корней уравнения или перейти к системе более простых уравнений.
Так метод оценки позволяет сделать вывод, что уравнение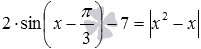 
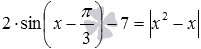
не имеет решений. Действительно, для частей этого уравнения справедливы следующие оценки 
и 
, из них следует, что равенство не достигается ни при каких значениях переменной.
А для уравнения 
можно получить такие оценки значений его частей: 
и 
. Они позволяют перейти от исходного уравнения к равносильной ему системе уравнений 
, из которой находится единственный корень уравнения 
.
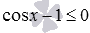
Переход, осуществленный в предыдущем примере, базируется на следующем утверждении:
Уравнение g(x)=h(x) , на ОДЗ для которого значения одного из выражений f(x) и g(x) не больше некоторого числа C , а значения другого – не меньше числа C (пусть g(x)≤C , h(x)≥C ), равносильно системе уравнений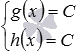 
.
Доказательство этого утверждения, а также доказательства других утверждений, на которых базируется метод оценки, вместе с рекомендациями по получению оценок и решениями характерных примеров, приведены в статье «Метод оценки».
Источник
Функционально- графический метод решения уравнений
ФУНКЦИОНАЛЬНО-ГРАФИЧЕСКИЙ МЕТОД РЕШЕНИЯ УРАВНЕНИЙ (использование свойств монотонности функций при решении уравнений.)
На доске записан эпиграф
Что есть лучшего?
Сравнив прошедшее, свести его
1 этап: актуализация прошлого опыта.
На предыдущих занятиях элективного курса мы систематизировали наши знания о решении уравнений и пришли к выводу, что уравнения любых видов можно решать общими методами. Какие общие методы решения уравнений мы выделили?
(Замена уравнения h ( f ( x ))= h ( g ( x ) уравнением f ( x )= g ( x ),
разложение на множители, введение новой переменной.)
2 этап: мотивация введения новых уравнений, решение которых связано с применением функционально-графического метода.
На этом занятии мы познакомимся еще с одним методом решения уравнений. Чтобы осознать его необходимость, выполним следующую работу.
Задание. Перед вами ряд уравнений. Сгруппируйте уравнения по методам решения. В таблицу запишите только номера уравнений. Можно поработать самостоятельно, затем сравнить ответы в парах или группах.
Учащиеся зачитывают ответы.
Среди уравнений вам встретились уравнения, которые вы не можете решить изученными методами. Многие из них решаются графическим методом. Его идея вам знакома. Напомните ее.
( 1). Преобразовать уравнение к виду f ( x )= g ( x ) так, чтобы в левой и правой части уравнения были известные нам функции. 2). В одной системе координат построить графики функций f ( x ) и g ( x ). 3). Найти абсциссы точек пересечения графиков. Это и будут приближенные корни уравнения.)
В некоторых случаях построение графиков функций можно заменить ссылкой на какое-либо свойство функций (поэтому и говорим не о графическом, а функционально-графическом методе решения уравнений).
Одно из свойств- это свойство монотонности функций. Это свойство применяется при решении уравнений вида
Актуализация опорных знаний учащихся о свойствах монотонности функций
Обращение к эпиграфу урока.
Задание. Вспомним, какие из изученных функций являются монотонными на области определения функции и назовем характер монотонности.
Источник
