Решение тригонометрических уравнений способом неравенств

Решение тригонометрических уравнений способом неравенств

Методы решения тригонометрических уравнений.

1. Алгебраический метод.

( метод замены переменной и подстановки ).

2. Разложение на множители.

П р и м е р 1. Решить уравнение: sin x + cos x = 1 .

Р е ш е н и е . Перенесём все члены уравнения влево:

sin x + cos x – 1 = 0 ,

преобразуем и разложим на множители выражение в

левой части уравнения:

П р и м е р 2. Решить уравнение: cos 2 x + sin x · cos x = 1.

Р е ш е н и е . cos 2 x + sin x · cos x – sin 2 x – cos 2 x = 0 ,

sin x · cos x – sin 2 x = 0 ,

sin x · ( cos x – sin x ) = 0 ,

П р и м е р 3. Решить уравнение: cos 2 x – cos 8 x + cos 6 x = 1.

Р е ш е н и е . cos 2 x + cos 6 x = 1 + cos 8 x ,

2 cos 4x cos 2x = 2 cos ² 4x ,

cos 4x · ( cos 2x – cos 4x ) = 0 ,

cos 4x · 2 sin 3x · sin x = 0 ,

1). cos 4x = 0 , 2). sin 3x = 0 , 3). sin x = 0 ,

3. Приведение к однородному уравнению.

а) перенести все его члены в левую часть;

б) вынести все общие множители за скобки;

в) приравнять все множители и скобки нулю;

г ) скобки, приравненные нулю, дают однородное уравнение меньшей степени, которое следует разделить на

cos ( или sin ) в старшей степени;

д) решить полученное алгебраическое уравнение относительно tan .

П р и м е р . Решить уравнение: 3 sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.

Р е ш е н и е . 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x ,

sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,

tan 2 x + 4 tan x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,

корни этого уравнения: y ₁ = — 1, y ₂ = — 3, отсюда

1) tan x = –1, 2) tan x = –3,

4. Переход к половинному углу.

П р и м е р . Решить уравнение: 3 sin x – 5 cos x = 7.

Р е ш е н и е . 6 sin ( x / 2 ) · cos ( x / 2 ) – 5 cos ² ( x / 2 ) + 5 sin ² ( x / 2 ) =

= 7 sin ² ( x / 2 ) + 7 cos ² ( x / 2 ) ,

2 sin ² ( x / 2 ) – 6 sin ( x / 2 ) · cos ( x / 2 ) + 12 cos ² ( x / 2 ) = 0 ,

tan ² ( x / 2 ) – 3 tan ( x / 2 ) + 6 = 0 ,

5. Введение вспомогательного угла.

где a , b , c – коэффициенты; x – неизвестное.

Теперь коэффициенты уравнения обладают свойствами синуса и косинуса , а именно : модуль ( абсолютное значение ) каждого из них не больше 1, а сумма их квадратов равна 1 . Тогда можно обозначить их соответственно как cos и sin ( здесь — так называемый вспомогательный угол ), и наше уравнение прини мает вид:

6. Преобразование произведения в сумму.

П р и м е р . Решить уравнение: 2 sin x · sin 3 x = cos 4 x .

Р е ш е н и е . Преобразуем левую часть в сумму:

Источник

Как научить решать тригонометрические уравнения и неравенства: методика преподавания

Курс математики корпорации «Российский учебник», авторства Георгия Муравина и Ольги Муравиной, предусматривает постепенный переход к решению тригонометрических уравнений и неравенств в 10 классе, а также продолжение их изучения в 11 классе. Представляем вашему вниманию этапы перехода к теме с выдержками из учебника «Алгебра и начало математического анализа» (углубленный уровень).

1. Синус и косинус любого угла (пропедевтика к изучению тригонометрических уравнений)

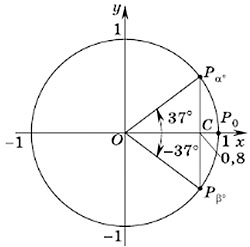
Пример задания. Найти приближенно углы, косинусы которых равны 0,8.

Решение. Косинус — это абсцисса соответствующей точки единичной окружности. Все точки с абсциссами, равными 0,8, принадлежат прямой, параллельной оси ординат и проходящей через точку C(0,8; 0). Эта прямая пересекает единичную окружность в двух точках: P_α° и P_β°, симметричных относительно оси абсцисс.

С помощью транспортира находим, что угол α° приближенно равен 37°. Значит, общий вид углов поворота с конечной точкой P_α°:

α° ≈ 37° + 360°n, где n — любое целое число.

В силу симметрии относительно оси абсцисс точка P_β° — конечная точка поворота на угол –37°. Значит, для нее общий вид углов поворота:

β° ≈ –37° + 360°n, где n — любое целое число.

Ответ: 37° + 360°n, –37° + 360°n, где n— любое целое число.

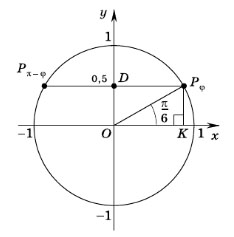
Пример задания. Найти углы, синусы которых равны 0,5.

Решение. Синус — это ордината соответствующей точки единичной окружности. Все точки с ординатами, равными 0,5, принадлежат прямой, параллельной оси абсцисс и проходящей через точку D(0; 0,5).

Эта прямая пересекает единичную окружность в двух точках: P_φ и P_π–φ, симметричных относительно оси ординат. В прямоугольном треугольнике OKP_φ катет KP_φ равен половине гипотенузы OPφ, значит,

Общий вид углов поворота с конечной точкой P_φ:

где n — любое целое число. Общий вид углов поворота с конечной точкой P_π–φ:

где n — любое целое число.

Ответ: где n — любое целое число.

2. Тангенс и котангенс любого угла (пропедевтика к изучению тригонометрических уравнений)

Пример 2. Найти общий вид углов, тангенс которых равен –1,2.

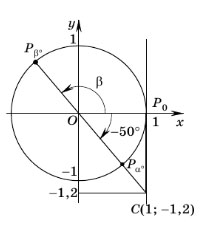
Пример задания. Найти общий вид углов, тангенс которых равен –1,2.

Решение. Отметим на оси тангенсов точку C с ординатой, равной –1,2, и проведем прямую OC. Прямая OC пересекает единичную окружность в точках P_α° и P_β° — концах одного и того же диаметра. Углы, соответствующие этим точкам, отличаются друг от друга на целое число полуоборотов, т.е. на 180°n (n — целое число). С помощью транспортира находим, что угол P_α° OP₀ равен –50°. Значит, общий вид углов, тангенс которых равен –1,2, следующий: –50° + 180°n (n — целое число)

По синусу и косинусу углов 30°, 45° и 60° легко найти их тангенсы и котангенсы. Например,

Перечисленные углы довольно часто встречаются в разных задачах, поэтому полезно запомнить значения тангенса и котангенса этих углов.

Источник

Простейшие и сложные тригонометрические неравенства

Неравенства – это соотношения вида a › b, где a и b – есть выражения, содержащие как минимум одну переменную. Неравенства могут быть строгими – ‹, › и нестрогими – ≥, ≤.

Тригонометрические неравенства представляют собой выражения вида: F(x) › a, F(x) ‹ a, F(x) ≤ a, F(x) ≥ a, в которых F(x) представлено одной или несколькими тригонометрическими функциями.

Простейшие тригонометрические неравенства

Примером простейшего тригонометрического неравенства является: sin x ‹ 1/2. Решать подобные задачи принято графически, для этого разработаны два способа.

Способ 1 – Решение неравенств с помощью построения графика функции

Чтобы найти промежуток, удовлетворяющий условиям неравенство sin x ‹ 1/2, необходимо выполнить следующие действия:

1. На координатной оси построить синусоиду y = sin x.
2. На той же оси начертить график числового аргумента неравенства, т. е. прямую, проходящую через точку ½ ординаты ОY.
3. Отметить точки пересечения двух графиков.
4. Заштриховать отрезок являющийся, решением примера.

Когда в выражении присутствуют строгие знаки, точки пересечения не являются решениями. Так как наименьший положительный период синусоиды равен 2π, то запишем ответ следующим образом:

Если знаки выражения нестрогие, то интервал решений необходимо заключить в квадратные скобки – [ ]. Ответ задачи можно также записать в виде очередного неравенства:

Способ 2 – Решение тригонометрических неравенств с помощью единичной окружности

Подобные задачи легко решаются и с помощью тригонометрического круга. Алгоритм поиска ответов очень прост:

1. Сначала стоит начертить единичную окружность.
2. Затем нужно отметить значение аркфункции аргумента правой части неравенства на дуге круга.
3. Нужно провести прямую проходящую через значение аркфункции параллельно оси абсциссы (ОХ).
4. После останется только выделить дугу окружности, являющуюся множеством решений тригонометрического неравенства.
5. Записать ответ в требуемой форме.

Разберем этапы решения на примере неравенства sin x › 1/2. На круге отмечены точки α и β – значения

Точки дуги, расположенные выше α и β, являются интервалом решения заданного неравенства.

Если нужно решить пример для cos, то дуга ответов будет располагаться симметрично оси OX, а не OY. Рассмотреть разницу между интервалами решений для sin и cos можно на схемах приведенных ниже по тексту.

Графические решения для неравенств тангенса и котангенса будут отличаться и от синуса, и от косинуса. Это обусловлено свойствами функций.

Арктангенс и арккотангенс представляют собой касательные к тригонометрической окружности, а минимальный положительный период для обеих функций равняется π. Чтобы быстро и правильно пользоваться вторым способом, нужно запомнить на какой из оси откладываются значения sin, cos, tg и ctg.

Касательная тангенс проходит параллельно оси OY. Если отложить значение arctg a на единичном круге, то вторая требуемая точка будет расположено в диагональной четверти. Углы

являются точками разрыва для функции, так как график стремится к ним, но никогда не достигает.

В случае с котангенсом касательная проходит параллельно оси OX, а функция прерывается в точках π и 2π.

Сложные тригонометрические неравенства

Если аргумент функции неравенства представлен не просто переменной, а целым выражением содержащим неизвестную, то речь уже идет о сложном неравенстве. Ход и порядок его решения несколько отличаются от способов описанных выше. Допустим необходимо найти решение следующего неравенства:

Графическое решение предусматривает построение обычной синусоиды y = sin x по произвольно выбранным значениям x. Рассчитаем таблицу с координатами для опорных точек графика:

В результате должна получиться красивая кривая.

Для простоты поиска решения заменим сложный аргумент функции

Пересечение двух графиков позволяет определить область искомых значений, при которых выполняется условие неравенства.

Найденный отрезок является решением для переменной t:

Однако, цель задания найти все возможные варианты неизвестной x:

Решить двойное неравенство достаточно просто, нужно перенести π/3 в крайние части уравнения и произвести требуемые вычисления:

Ответ на задание будет выглядеть как интервал для строгого неравенства:

Подобные задачи потребует опыта и сноровки учащихся в обращении с тригонометрическими функциями. Чем больше тренировочных заданий будет решено в процессе подготовке, тем проще и быстрее школьник найдет ответ на вопрос ЕГЭ теста.

Источник