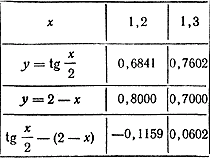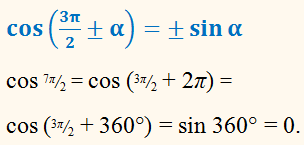Решение тригонометрических уравнений графическим способом примеры

Решение тригонометрических уравнений графически

Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.

Пусть, например, нужно решить уравнение

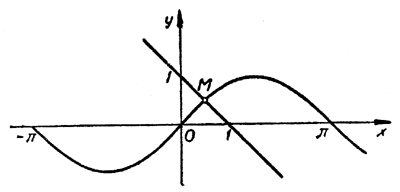
На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х

Эти графики пересекаются в одной точке М. Абсцисса этой точки и дает нам единственный корень нашего уравнения:

Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы. При х = 0,5

следовательно, sin х 1 — х. Но тогда, как легко понять из того же рисунка, искомый корень x₀ должен быть меньше, чем 0,6. Теперь уже мы знаем, что x₀ находится в интервале [0,5; 0,6]. Поэтому с точностью до 0,1

С помощью таблиц можно найти приближенное значение x₀ и с точностью до 0,01. Разделим интервал [0,5; 0,6] пополам. В средней точке (x = 0,55) этого интервала

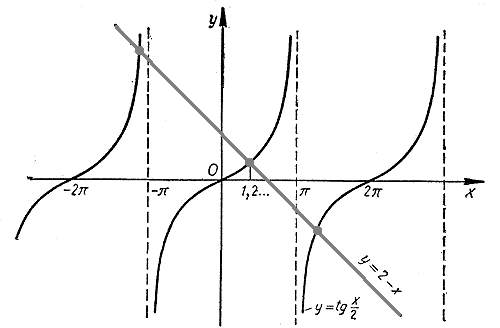
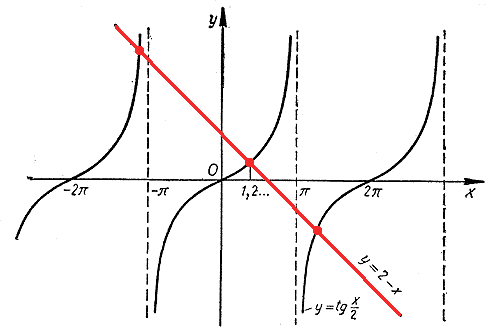
Графики функций у = tg x /₂ и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х₀. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.

Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /₂ и у = 2 — х в окрестности точки х = 1,2.

x	1,2	1,3
y=tg x/2	0,6841	0,7602
y=2-x	0,8000	0,7000
tg x/2-(2-x)	-0,1159	0,0602

Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /₂ — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х₀ ≈ 1,2 (с недостатком) или х₀ ≈ 1,3 (с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня
с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25

Источник

Решение тригонометрических уравнений графическим способом примеры

Графический способ решения тригонометрических уравнений

О графическом способе решения некоторых тригонометрических уравнений мы уже говорили в части I. Теперь, умея строить графики тригонометрических функций кратных углов, мы можем решать этим способом гораздо больше уравнений, чем прежде. Но основная идея решения, конечно, остается той же самой.

Для примера рассмотрим уравнение

Графики функций у = tg x /₂ и у = 2 — х пересекаются в бесконечном числе точек. Значит, данное уравнение имеет бесконечное множество корней. Найдем, например, наименьший положительный корень х₀. Этот корень является абсциссой точки пересечения графиков. Примерно он равен 1,2.

Чтобы найти этот корень точнее, воспользуемся таблицами тангенсов В. М. Брадиса (или рассчитаем соответствующие значения в программе «Kалькулятор» или «Excel»). Выпишем значения функций у = tg x /₂ и у = 2 — х в окрестности точки х = 1,2.

Как видно из этой таблицы, при переходе от значения х = 1,2 к значению х = 1,3 разность tg x /₂ — (2 — х) меняет свой знак на противоположный (с — на +). Значит, в нуль эта разность обращается где-то между значениями 1,2 и 1,3. Следовательно, с точностью до 0,1 х₀ ≈ 1,2 (с недостатком) или х₀ ≈ 1,3(с избытком). Используя таблицу тангенсов, можно найти и приближенное значение этого корня с точностью до 0,01. Для этого рассмотрим значение х = 1,25, являющееся средним значением чисел 1,2 и 1,3. При х = 1,25

1,26 x /₂ и 2 — х в точке х = 1,27. Предлагаем учащимся сделать это самостоятельно.

1. Найти наименьший положительный корень уравнения

Источник

Решение тригонометрических уравнений и неравенств функционально-графическим способом.

Тема: Практическое занятие по теме «Решение тригонометрических уравнений и неравенств функционально-графическим способом».

Решение тригонометрических уравнений графически

Уравнения, с которыми приходится сталкиваться при решении практических задач, как правило, значительно отличаются от тех, которые мы рассматривали. Для таких уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. Современная математика располагает эффективными методами приближенного решения уравнений. Рассмотрим графический способ решения.

ПРИМЕР1: Пусть, например, нужно решить уравнение sin х = 1 — х .

На одном и том же рисунке начертим два графика: график функции y = sin х и график функции у = 1 — х

Эти графики пересекаются в одной точке М. Абсцисса этой точки, и дает нам единственный корень нашего уравнения.

ПРИМЕР 2: Решить уравнение и неравенство графическим способом на интервале (-

На одном и том же рисунке начертим два графика: график функции и график функции у = .

У нас получилось 4 точки пересечения на интервале (-. Абсциссы этих точек и являются решением уравнения. А интервалы, на которых график находится выше прямой у = , являются решением неравенства.

Задание: Выполнить уравнения и неравенства

Решите на интервале ( : А) уравнение 0

«4» — №1, №2 №3 одну из систем

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

• Сейчас обучается 812 человек из 76 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

• Сейчас обучается 286 человек из 69 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

• Сейчас обучается 599 человек из 75 регионов

Ищем педагогов в команду «Инфоурок»

В данной работе представлен краткий материал для самостоятельного изучения студентами темы «Решение тригонометрических уравнений и неравенств функционально-графическим способом».Длярешения уравнений иногда вообще нельзя указать никакого способа, который позволял бы найти корни абсолютно точно. В таком случае приходится ограничиваться нахождением лишь приближенных значений корней. И тогда используем графический способ.

Номер материала: ДБ-1225097

Международная дистанционная олимпиада Осень 2021

Не нашли то что искали?

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Спортивные и творческие кружки должны появиться в каждой школе до 2024 года

Время чтения: 1 минута

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В России выбрали топ-10 вузов по работе со СМИ и контентом

Время чтения: 3 минуты

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Уроки математики и физики для школьников и родителей

понедельник, 23 марта 2020 г.

Урок 4. Графический метод решения тригонометрических уравнений

ВИДЕО УРОК

Чтобы графически решить уравнение

необходимо построить графики функций

и найти абсциссы точек пересечения построенных графиков.

Решить графически уравнение :

–0,5 x 2 – х + 2,625 = со s πx .

Сначала нужно определиться с методом решения уравнения. Очевидно, никакие преобразования уравнения не дают возможности перейти к каким-либо более простым уравнениям. В данном случае можно попробовать решить уравнение графическим методом. Здесь видно, что функции, отвечающие частям уравнения, довольно простые в плане построения их графиков. Поэтому построим в одной системе координат графики функций :

График квадратичной функции

это парабола. Вычислим координаты её вершины :

Нам известно поведение построенных функций. Это позволяет утверждать, что за пределами видимой области точек пересечения графиков нет. Значит, можно утверждать, что решаемое уравнение имеет два корня .

Определим абсциссы точек пересечения. По чертежу можно судить об их приближённых значениях :

Это есть приближённые значения корней решаемого уравнения.

Возможно, найденные значения являются точными значениями корней. Проверим это предположение, для чего выполним проверку подстановкой :

Сначала в уравнение

–0,5 x 2 – х + 2,625 = со s πx

Найдём значение со s 7π / ₂ , применяя следующую формулу приведения:

х ₁ = –3,5 – корень данного уравнения .

Затем в уравнение

–0,5 x 2 – х + 2,625 = со s πx

(–0,5)(1,5) 2 – 1,5 + 2,625 = со s π ∙ (1,5),

Найдём значение со s 3π / ₂ , применяя следующую формулу приведения:

х ₂ = 1,5 – тоже корень данного уравнения .

Проверка показала, что –3,5 и 1,5 – это корни уравнения :

Таким образом, графический метод позволил нам определит точные корни уравнения .

Решить графически уравнение :

На одном и том же рисунке начертим два графика :

и график функции у = 1 – x.

Для уточнения полученного результата полезно использовать тригонометрические таблицы или компьютерные программы .

Но тогда, как легко понять из рисунка, корень уравнения

Проверим значение х = 0,6 . Имеем (при х = 0,6 )

Но тогда, как легко понять из того же рисунка, искомый корень х ₀ должен быть меньше, чем 0,6 . Теперь мы знаем, что х ₀ находится в интервале

Поэтому с точностью до 0,1

С помощью таблиц можно найти приближённое значение х ₀ и с точностью до 0,01 . Разделим интервал

пополам. В средней точке (х = 0,55) этого интервала

Опять получаем, что

Проверим точку х = 0,52 (она близка к средней точке х = 0,525 интервала [0,50; 0,55] , в котором заключён корень х ₀ ).

Поэтому с точностью до 0,01

Источник