Решение тригонометрических неравенств графическим способом

О тригонометрических неравенствах: понятие, типы и особенности решения

Что такое тригонометрические неравенства

Тригонометрические неравенства — неравенства, в которых переменные находятся только под знаком тригонометрической функции.

Тригонометрические функции обозначаются как:

При доказательстве тригонометрических неравенств применяют общие приемы доказательства алгебраических неравенств.

Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.

При этом в тригонометрии спектр применяемых математических методов богаче.

К ним относятся:

• метод от обратного;
• аналитико-синтетический метод;
• методы математического анализа;
• метод математической индукции;
• элементы геометрии;
• векторная алгебра;
• графический метод.

Виды тригонометрических неравенств

Неравенства в тригонометрии подразделяются на два вида:

По однородности они делятся на два типа:

В однородных неравенствах у всех слагаемых степень одинакова по сумме.

Примеры таких неравенств:

В неоднородных — степени слагаемых будут отличаться друг от друга.

Простейшие

Простейшие тригонометрические неравенства имеют вид:

sin х m, cos x m, tg x m, ctg >m; ctg Пример

\(sin 3x — sin x > 0; \)

\(cos x — 5x + 2 > 0.\)

Методы решения тригонометрических неравенств

Общие сведения по решению тригонометрических неравенств

При решении тригонометрических неравенств используют свойство монотонности тригонометрических функций и промежутки их знакопостоянства.

Монотонность характерна как для убывающих, так и для возрастающих функций. Она означает, что в определенном промежутке большему по значению аргумента будет соответствовать большее или меньшее значение функции в зависимости от возрастания или убывания функции, соответственно.

О промежутках знакопостоянства говорят, когда множеству значений аргумента соответствуют только положительные или только отрицательные значения функции.

Чтобы решить простейшее тригонометрическое неравенство, необходимо найти множество всех значений аргумента, которые обращают данное неравенство в верное числовое неравенство.

Важные моменты в решении простейших тригонометрических неравенств:

sin x = 0, если \(\mathrm x=\mathrm<πR>, \ R\in Z;\)

sin x = -1, если \(x=-\frac\pi R+2\pi R\,, \ R\in Z;\)

sin x = 1, если \(x=\frac\pi2+2\pi R, \ R\in Z;\)

sin x > 0, если \(2\pi R

для cos x:

cos x = 0, если \(x=\frac\pi2+\pi R,\ R\in Z;\)

cos x = -1, если \ \(x=\pi+2\pi R, \ R\in Z;\)

cos x = 1, если \(x=2\pi R, \ R\in Z;\)

cos x > 0, если \(2\pi R-\frac\pi2

cos x \(2\pi R+\frac\pi2

tg x > 0, если \(\pi R

tg x \(\pi R-\frac\pi2

тангенс не существует, если \(x=\frac\pi2+\pi R, \ R\in Z.\)

Нестандартные способы решения тригонометрических неравенств включают в себя несколько методик:

1. Графический метод.
2. Метод постановки.
3. Метод интервалов.
4. Метод секторов.
5. Метод концентрических окружностей для систем тригонометрических неравенств.

Для решения простейших тригонометрических неравенств применяют графический способ решения и решение с помощью числовой окружности.

Решение тригонометрических неравенств с помощью единичной окружности

Решите неравенство: sin x > ½.

Построим единичную окружность. Построим на ней дуги AC и \(AC_1\) . Их синус должен быть равен ½.

Из окружности видно, что все дуги, начинающиеся в точке А и заканчивающиеся в любой внутренней точке дуги \(CBC_1\) , удовлетворяют данному неравенству.

Чтобы получить все решения данного неравенства, прибавим к концам этого промежутка 2πR.

Ответ: \(\frac\pi6+2\pi R

Решите неравенство: cos 3x > ½.

Обозначим 3х через α.

Неравенство примет вид:

Этому неравенству удовлетворяют все точки \[P_\alpha\] единичной окружности, абсциссы которых больше или равны -1/2.

На окружности видно, что эти точки дуги лежат на прямой \(х=-1/2\) или правее ее.

Выделенная на рисунке дуга представляет собой множество всех точек, удовлетворяющих данному неравенству. Концы этой дуги входят в искомое множество. Их абсциссы равны -1/2, значит, удовлетворяют неравенству.

Учитывая периодичность косинуса, запишем решения для неравенства

\(-\frac<2\pi>3+2\pi R\leq\alpha\leq\frac<2\pi>3+2\pi R, \ R\in Z.\)

Вернемся снова к переменной х, получим искомый ответ:

Решите неравенство: tg 2x > 1.

Обозначим 2х через α.

Неравенство примет вид:

Построим окружность и проведем касательную к окружности в точке (1; 0). Эта линия является тангенсом.

Так как α является решением неравенства tg α ≥ 1, то ордината точки \(T_\alpha\) линии тангенсов tg α должна быть равна или больше 1. Луч АТ имеет все эти точки.

Точки \(P_\alpha\) окружности, соответствующие точкам \( P_\alpha\) , образуют дугу.

Для ее точек выполняется неравенство \(\frac\pi4\leq\alpha

Прибавим к этому промежутку период тангенса и получим решение неравенства \(T_\alpha\geq1:\)

Так как \(α=2х\) , получим ответ:

Графическое решение тригонометрических неравенств

Для решения простейших тригонометрических неравенств с помощью графического метода решения строят график тригонометрической функции (sin x, cos x и т. д.) и прямую у=а. Затем выделяют промежутки с помощью построенных графиков. Эти промежутки являются решением неравенства.

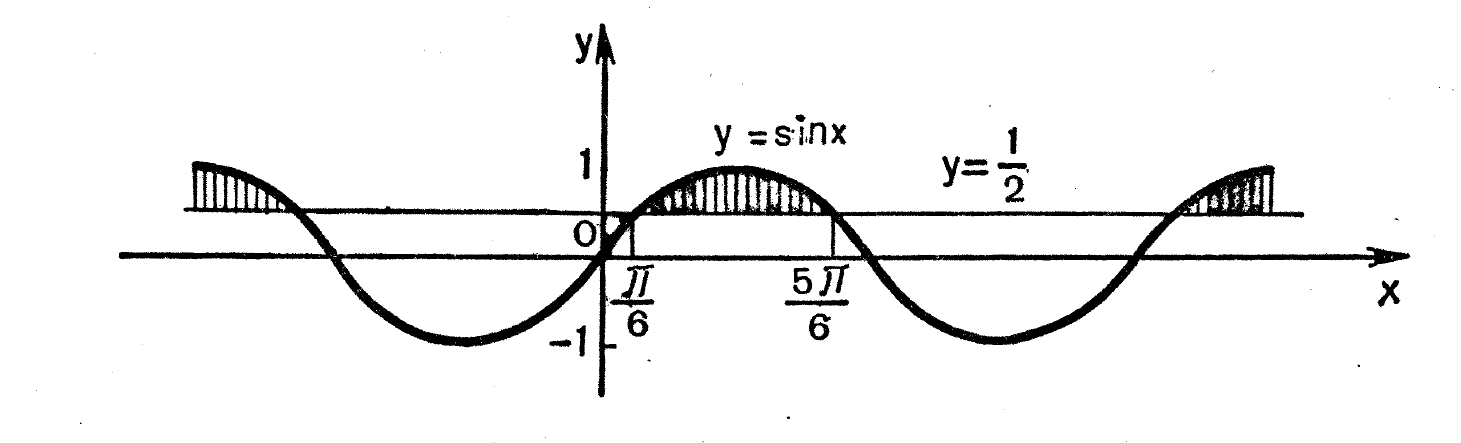
Решите неравенство: sin x > ½.

Построим графики функций \(y=sin\) \(x\) и \(y=1/2.\)

Из графика видно, что прямая у=1/2 пресекает синусоиду в бесконечном числе точек.

На нем выделены несколько значений аргументов, которые удовлетворяют данному неравенству: \(\frac\pi6, \frac<5\pi>6.\)

Учитывая периодичность синуса, запишем окончательный ответ:

\(\frac\pi6+2\pi R \(R\in Z.\)

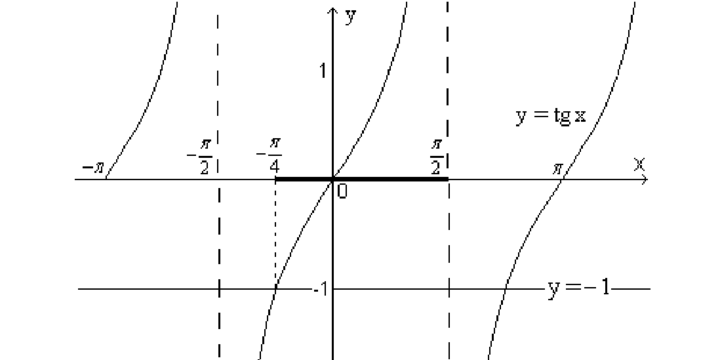
Решите неравенство: tg x ≥ -1.

Построим графики функций \(y = tg\) \(x \) и \(y = -1.\)

Из графика видно, что одним из промежутков, который удовлетворяет неравенств, является:

Учтем периодичность тангенса и получим:

Решение тригонометрических неравенств методом интервалов

Решите неравенство: \(6\sin^2\left(x\right)-5\sin\left(x\right)+1\geq0.\)

Введем новую переменную:

Тогда данное неравенство можно записать в другом виде:

Это неравенство представляет собой квадратное уравнение с корнями:

\(y_1=\frac12 \ и \ y_2=\frac13.\)

Получим из данного трехчлена линейные множители, используя формулу:

Используем метод интервалов для его решения.

Объединим промежутки \(y\geq\frac12\) и \(y\leq\frac13.\)

Тогда получим, что

\(\sin\left(x\right)\leq\frac13\) и \(\sin\left(x\right)\geqslant\frac12.\) (2)

Теперь для решения полученных неравенств применим алгоритм решения по методу единичной окружности.

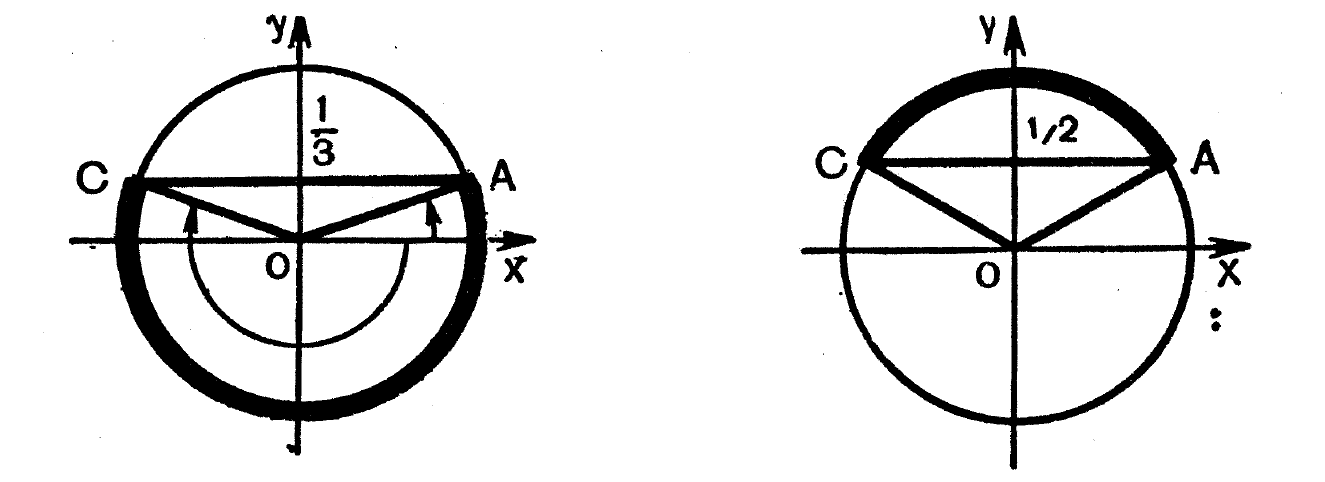
Решая неравенство (1), на построенной слева окружности видим, что ему удовлетворяют такие значения х:

\(-\pi-arc\sin\frac13\leq x\leq arc\sin\frac13\) . (3)

Для получения всех решений неравенства к полученному промежутку добавим \(2\pi R.\)

\(-\pi-arc\sin\;\frac13+2\pi R\leq x\leq arc\sin\;\frac13+2\pi R,\;R\in Z\) . (4)

Для решения неравенства (2) так же построим окружность и увидим, что ему удовлетворяют значения х:

\(\frac\pi6+2\pi R\leq x\leq\frac<5\pi>6+2\pi R,\;R\in Z.\) (5)

Значения х, удовлетворяющие неравенствам (4) и (5) являются решением данного неравенства.

Задача 2

Решите неравенство: \(\frac <15>

Введем новую переменную: \(у = cos x.\)

Неравенство примет вид:

После преобразований получим:

Используем метод интервалов.

Неравенство \(\cos\;x решения не имеет.

Так как \(-1\leqslant\cos\;x\leqslant\) , то неравенство \(\frac12 надо заменить другим неравенством:

Источник

Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом. 10-й класс

Класс: 10

Презентация к уроку

Оборудование: ПК, проектор, экран, аудиторная доска.

Тип занятия: изучение нового материала.

Образовательная цель:	сформировать навык решения тригонометрических неравенств, используя графический метод решения неравенств; отработать навыки построения графиков тригонометрических функций; познакомить учащихся с основоположниками тригонометрии и историей ее развития.
Развивающая цель:	обеспечить условия для развития умений анализировать, выделять главное, устанавливать единые общие признаки и свойства; научить применять знания на практике; научить критически оценивать свои знания.
Воспитательная цель:	воспитывать положительное отношение к знаниям; воспитывать дисциплинированность и добросовестность при выполнении заданий; воспитывать умение работать в парах (чувствовать индивидуальную ответственность за достижение результата).

Задачи:

• повторить следующие темы по математике: решение квадратных неравенств графическим способом, преобразование графиков тригонометрических функций, понятие arcsin, arccos, arctg и arcctg числа, решение тригонометрических уравнений;
• научить применять графический метод для решения тригонометрических неравенств;
• отработать навыки построения графиков тригонометрических функций;
• расширить кругозор учащихся об истории развития Тригонометрии;
• для активизации познавательной деятельности учащихся применять различные формы и методы работы на уроке: фронтальная, индивидуальная и групповая (работа в парах) формы работы, использование игровых технологий.

Структура занятия:

1. Организационный момент, проверка домашнего задания (3 мин.);
2. Актуализация опорных знаний и фиксация затруднений в деятельности (5 мин.);
3. Объяснение нового материала (10 мин.);
4. Экспертная работа (5 мин.);
5. Самостоятельная работа в парах (10 мин.);
6. Домашнее задание (2 мин.);
7. Игра “Поле чудес” (6 мин.);
8. Рефлексия деятельности (итог урока) (4 мин.).

Пояснение к уроку: во время урока учащиеся выставляют баллы в “Рабочую карту урока” согласно правилам, описанным в данной карте. В конце урока подводится итог работы учащихся по количеству набранных баллов.

1. Организационный момент, проверка домашнего задания

Французский писатель Анатоль Франс однажды заметил: “Учиться можно только весело… Чтобы переваривать знания, надо поглощать их с аппетитом.”.

Давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием.

Прежде чем приступить к изучению нового материала, проверим домашнее задание на сегодня.

Проверка домашнего задания:

№ 11.27 (а, б), № 11.29 (б, е), № 11.30 (б)

Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.

За каждое правильно выполненное задание – 1 балл в рабочую карту занятия в колонку “Домашняя работа”.

2. Актуализация опорных знаний и фиксация затруднений в деятельности

Тема нашего урока – Тригонометрические неравенства. Решение тригонометрических неравенств графическим способом.

Давайте запишем дату и тему урока в тетрадь.

Перед Вами на сегодня стоит задача – научиться применять графический метод для решения тригонометрических неравенств.

Поработаем сначала устно, чтобы вспомнить те понятия и приемы, которые нам понадобятся для изучения новой темы.

За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.

Инструкция по работе с презентацией: при подведении курсора к ответу и нажатии левой кнопки мыши: неверные ответы исчезают, а в области верного ответа всплывает окно со словом “Верно”.

3. Объяснение нового материала

Если вспомнить определение тригонометрического уравнения – это уравнение, содержащее переменную под знаком тригонометрической функции, тогда легко можно дать определение тригонометрического неравенства – это неравенство, содержащие переменную под знаком тригонометрической функции.

Для решения тригонометрических неравенств мы будем использовать графический метод.

Рассмотрим решение неравенства

Построим график функции: и проведём прямую .

Определим точки пересечения данных графиков:

Заштрихуем область, при которой значения функции больше

, если, например,

Так как функция периодическая (Т=), значит, ,

Ответ: ,

Рассмотрим решение неравенства

Пусть . Получим неравенство

Рассмотрим графики функций и Множество решений неравенства составляют абсциссы точек графика расположенных выше точек графика

Получим неравенство

Следовательно,

Ответ: , [2].

4. Экспертная работа

К доске приглашаются двое учащихся, хорошо разобравшихся в материале и желающих ответить у доски, они будут выступать в роли экспертов, остальные учащиеся могут поправлять их решение по мере надобности с места.

1. Ответ: ,

2. Ответ: ,

За работу у доски учащиеся получают 1-3 балла, за работу с места 1 балл.

5. Самостоятельная работа в парах

Прежде чем перейти к выполнению самостоятельной работы, необходимо заметить, что при решении более сложных тригонометрических неравенств, их с помощью преобразований сводят к простейшим тригонометрическим неравенствам, используя при этом те же приёмы, что и при решении тригонометрических уравнений.

Учащиеся выполняют задание, обмениваются тетрадями и проверяют работу соседа по парте, выставляя соответствующие баллы, ответы представлены на экране, подробное решение неравенств под номером 3 необходимо заранее подготовить на аудиторной доске.

Для решения тригонометрических неравенств графическим методом можно использовать Приложение № 2 к данному уроку.

Вариант № 1 Решить неравенства	Вариант № 2 Решить неравенства
1.	1.
2.	2.

За каждое верное задание № 1,2-1 балл, № 3 – 3 балла.

Подведение итогов изучения новой темы. Учащимся необходимо ответить на вопросы учителя.

Вопросы:

• Какой метод мы использовали для решения тригонометрических неравенств?
• Что необходимо предпринять, чтобы решить тригонометрическое неравенство графическим способом?
• Как влияет периодичность тригонометрических функций на ответ при решении тригонометрических неравенств?

За каждый правильный ответ учащиеся получают 1 балл в рабочую карту занятия в колонку “Устная работа”.

6. Домашнее задание

Никольский С. М. Алгебра и начала математического анализа. 10 класс – М.: Просвещение, 2013.

п. 11.5, 11.6, № 11.34 (б), 11.36 (в), 11.37 (в), 11.38 (б), 11.41 (б)

Дополнительное задание (по желанию):

Решить неравенство

7. Игра “Поле чудес”

Игра построена по принципу одноименной телевизионной игры. Учитель читает задание, учащиеся могут открыть любую букву, если выполнят скрытое в данной ячейке задание.

За каждую угаданную букву (решенное задание) учащиеся получают 1 балл, за отгаданное слово – 5 баллов.

Инструкция по работе с презентацией: при подведении курсора к ячейке, за которой скрывается буква, и нажатии левой кнопки мыши: появляется задание, которое необходимо выполнить, при повторном нажатии левой кнопки мыши в данную область появляется скрытая там буква.

Древнегреческий астроном, географ и математик II века до н.э., часто называемый величайшим астрономом античности. Главной заслугой его считается то, что он привнёс в греческие геометрические модели движения небесных тел предсказательную точность астрономии Древнего Вавилона.

При разработке теорий Луны и Солнца он использовал античный вариант тригонометрии. Возможно, он первым составил таблицу хорд, аналог современных таблиц тригонометрических функций.

Швейцарский, немецкий и российский математик, внёсший значительный вклад в развитие математики, а также механики, физики, астрономии и ряда прикладных наук.

Автор более чем 800 работ по математическому анализу, дифференциальной геометрии, теории чисел, приближённым вычислениям, небесной механике, математической физике, оптике, баллистике, кораблестроению, теории музыки и др.

Почти полжизни провёл в России, где внёс существенный вклад в становление российской науки. С 1731 по 1741, а также с 1766 года был академиком Петербургской Академии Наук (в 1741—1766 годах работал в Берлине, оставаясь одновременно почётным членом Петербургской Академии). Хорошо знал русский язык и часть своих сочинений (особенно учебники) публиковал на русском. Первые русские академики-математики (С.К. Котельников) и астрономы (С.Я. Румовский) были его учениками.

Аналитическая теория тригонометрических функций в основном была создана этим выдающимся математиком XVIII века. Именно он первым ввел известные определения тригонометрических функций, стал рассматривать функции произвольного угла, получил формулы приведения.

Ответ: Леонард Эйлер

Наука об измерении треугольников. Данный термин впервые появился в 1595 г. как название книги немецкого математика Бартоломеуса Питискуса, а сама наука ещё в глубокой древности использовалась для расчётов в астрономии, геодезии и архитектуре..

Раздел математики, в котором изучаются тригонометрические функции и их приложения к геометрии.

Рефлексия деятельности (итог урока)

Рабочая карта занятия Учащегося ________________________ ____ “ ” класса

о/т — оценка товарища, о/у- оценка учителя, с/о – самооценка, о/г-оценка группы Домашняя работа
с/о

Общее количество баллов, по 1 за каждое правильно выполненное задание. Устная работа
о/у

Общее количество баллов, по 1 за каждый правильный ответ. Экспертная работа (работа у доски)
о/г

1-3 балла за работу у доски,

1 балл за работу с места. Самостоятельная работа в парах
о/т

За каждое верное задание

№ 3 – 3 балла. Игра “Поле чудес”
о/у

Общее количество баллов, по 1 за каждый правильный ответ, за отгаданное слово – 5 баллов. Итог: _____ Итог: _____ Итог: _____ Итог: _____ Итог: _____ Итог: общее кол-во баллов ___/ Оценка ___

• 16 и более баллов – оценка “5”
• 11 — 15 баллов – оценка “4”
• 6 — 10 баллов – оценка “3”

Литература:

1. Никольский, С.М. Алгебра и начала математического анализа. 10 класс: учеб. для общеобразоват. учреждений: базовый и профил. уровни/ С. М. Никольский, М.К. Потапов, Н.Н. Решетников, А.В. Шевкин. – М.: Просвещение, 2013.
2. Чулков, П.В. Материалы курса “Уравнения и неравенства в школьном курсе математики”: Лекции 5-8./ П.В. Чулков. – М.: Педагогический университет “Первое сентября”, 2010.
3. Егерев, В.К. Сборник задач по математике для поступающих во втузы: учеб. пособие/ В.К. Егерев, Б.А. Кордемский, В.В. Зайцев и др.; Под ред. М.И. Сканави. – М.: “Столетие”, 1997.

Источник