Решение теоремы пифагора разными способами

Разные способы доказательства теоремы Пифагора: примеры, описание и отзывы

В одном можно быть уверенным на все сто процентов, что на вопрос, чему равен квадрат гипотенузы, любой взрослый человек смело ответит: «Сумме квадратов катетов». Эта теорема прочно засела в сознании каждого образованного человека, но достаточно лишь попросить кого-либо ее доказать, и тут могут возникнуть сложности. Поэтому давайте вспомним и рассмотрим разные способы доказательства теоремы Пифагора.

Краткий обзор биографии

Теорема Пифагора знакома практически каждому, но почему-то биография человека, который произвел ее на свет, не так популярна. Это поправимо. Поэтому прежде чем изучить разные способы доказательства теоремы Пифагора, нужно кратко познакомиться с его личностью.

Пифагор – философ, математик, мыслитель родом из Древней Греции. Сегодня очень сложно отличить его биографию от легенд, которые сложились в память об этом великом человеке. Но как следует из трудов его последователей, Пифагор Самосский родился на острове Самос. Его отец был обычный камнерез, а вот мать происходила из знатного рода.

Судя по легенде, появление на свет Пифагора предсказала женщина по имени Пифия, в чью честь и назвали мальчика. По ее предсказанию рожденный мальчик должен был принести много пользы и добра человечеству. Что вообще-то он и сделал.

Рождение теоремы

В юности Пифагор переехал с острова Самос в Египет, чтобы встретиться там с известными египетскими мудрецами. После встречи с ними он был допущен к обучению, где и познал все великие достижения египетской философии, математики и медицины.

Вероятно, именно в Египте Пифагор вдохновился величеством и красотой пирамид и создал свою великую теорию. Это может шокировать читателей, но современные историки считают, что Пифагор не доказывал свою теорию. А лишь передал свое знание последователям, которые позже и завершили все необходимые математические вычисления.

Как бы там ни было, сегодня известна не одна методика доказательства данной теоремы, а сразу несколько. Сегодня остается лишь гадать, как именно древние греки производили свои вычисления, поэтому здесь рассмотрим разные способы доказательства теоремы Пифагора.

Теорема Пифагора

Прежде чем начинать какие-либо вычисления, нужно выяснить, какую теорию предстоит доказать. Теорема Пифагора звучит так: «В треугольнике, у которого один из углов равен 90 о , сумма квадратов катетов равна квадрату гипотенузы».

Всего существует 15 разных способов доказательства теоремы Пифагора. Это достаточно большая цифра, поэтому уделим внимание самым популярным из них.

Способ первый

Сначала обозначим, что нам дано. Эти данные будут распространяться и на другие способы доказательств теоремы Пифагора, поэтому стоит сразу запомнить все имеющееся обозначения.

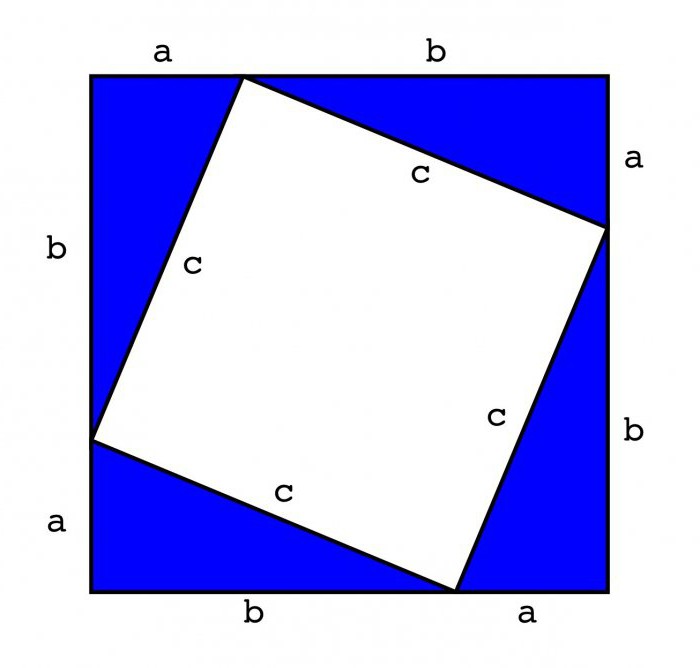
Допустим, дан прямоугольный треугольник, с катетами а, в и гипотенузой, равной с. Первый способ доказательства основывается на том, что из прямоугольного треугольника нужно дорисовать квадрат.

Чтобы это сделать, нужно к катету длиной а дорисовать отрезок равный катету в, и наоборот. Так должно получиться две равные стороны квадрата. Остается только нарисовать две параллельные прямые, и квадрат готов.

Внутри получившейся фигуры нужно начертить еще один квадрат со стороной равной гипотенузе исходного треугольника. Для этого от вершин ас и св нужно нарисовать два параллельных отрезка равных с. Таким образом, получиться три стороны квадрата, одна из которых и есть гипотенуза исходного прямоугольного треугольники. Остается лишь дочертить четвертый отрезок.

На основании получившегося рисунка можно сделать вывод, что площадь внешнего квадрата равна (а+в) 2 . Если заглянуть внутрь фигуры, можно увидеть, что помимо внутреннего квадрата в ней имеется четыре прямоугольных треугольника. Площадь каждого равна 0,5ав.

Поэтому площадь равна: 4*0,5ав+с 2 =2ав+с 2

Отсюда (а+в) 2 =2ав+с 2

И, следовательно, с 2 =а 2 +в 2

Способ два: подобные треугольники

Данная формула доказательства теоремы Пифагора была выведена на основании утверждения из раздела геометрии о подобных треугольниках. Оно гласит, что катет прямоугольного треугольника – среднее пропорциональное для его гипотенузы и отрезка гипотенузы, исходящего из вершины угла 90 о .

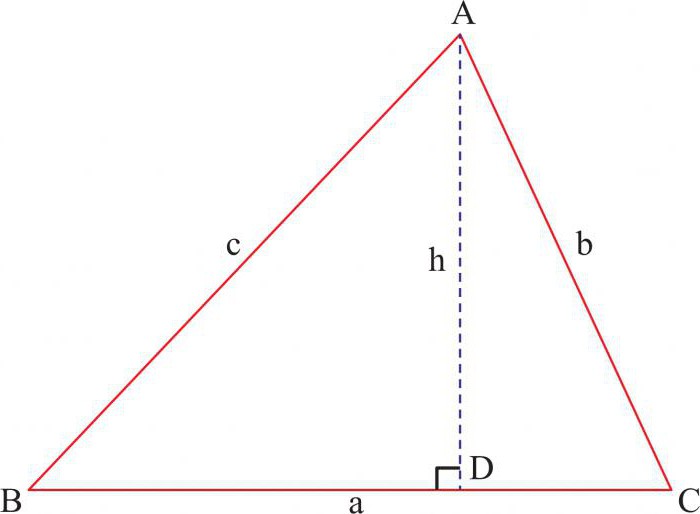
Исходные данные остаются те же, поэтому начнем сразу с доказательства. Проведем перпендикулярный стороне АВ отрезок СД. Основываясь на вышеописанном утверждении катеты треугольников равны:

Чтобы ответить на вопрос, как доказать теорему Пифагора, доказательство нужно проложить возведением в квадрат обоих неравенств.

АС 2 =АВ*АД и СВ 2 =АВ*ДВ

Теперь нужно сложить получившиеся неравенства.

АС 2 + СВ 2 =АВ*(АД*ДВ), где АД+ДВ=АВ

АС 2 + СВ 2 =АВ*АВ

АС 2 + СВ 2 =АВ 2

Доказательство теоремы Пифагора и различные способы ее решения нуждаются в разностороннем подходе к данной задаче. Однако этот вариант является одним из простейших.

Еще одна методика расчетов

Описание разных способов доказательства теоремы Пифагора могут ни о чем не сказать, до тех самых пор пока самостоятельно не приступишь к практике. Многие методики предусматривают не только математические расчеты, но и построение из исходного треугольника новых фигур.

В данном случае необходимо от катета ВС достроить еще один прямоугольный треугольник ВСД. Таким образом, теперь имеется два треугольника с общим катетом ВС.

Зная, что площади подобных фигур имеют соотношение как квадраты их сходных линейных размеров, то:

Поскольку из разных способов доказательств теоремы Пифагора для 8 класса этот вариант едва ли подойдет, можно воспользоваться следующей методикой.

Самый простой способ доказать теорему Пифагора. Отзывы

Как полагают историки, этот способ был впервые использован для доказательства теоремы еще в древней Греции. Он является самым простым, так как не требует абсолютно никаких расчетов. Если правильно начертить рисунок, то доказательство утверждения, что а 2 +в 2 =с 2 , будет видно наглядно.

Условия для данного способа будет немного отличаться от предыдущего. Чтобы доказать теорему, предположим, что прямоугольный треугольник АВС – равнобедренный.

Гипотенузу АС принимаем за сторону квадрата и дочерчиваем три его стороны. Кроме этого необходимо провести две диагональные прямые в получившемся квадрате. Таким образом, чтобы внутри него получилось четыре равнобедренных треугольника.

К катетам АВ и СВ так же нужно дочертить по квадрату и провести по одной диагональной прямой в каждом из них. Первую прямую чертим из вершины А, вторую – из С.

Теперь нужно внимательно всмотреться в получившийся рисунок. Поскольку на гипотенузе АС лежит четыре треугольника, равные исходному, а на катетах по два, это говорит о правдивости данной теоремы.

Кстати, благодаря данной методике доказательства теоремы Пифагора и появилась на свет знаменитая фраза: «Пифагоровы штаны во все стороны равны».

Доказательство Дж. Гарфилда

Джеймс Гарфилд – двадцатый президент Соединенных Штатов Америки. Кроме того, что он оставил свой след в истории как правитель США, он был еще и одаренным самоучкой.

В начале своей карьеры он был обычным преподавателем в народной школе, но вскоре стал директором одного из высших учебных заведений. Стремление к саморазвитию и позволило ему предложить новую теорию доказательства теоремы Пифагора. Теорема и пример ее решения выглядит следующим образом.

Сначала нужно начертить на листе бумаги два прямоугольных треугольника таким образом, чтобы катет одного из них был продолжением второго. Вершины этих треугольников нужно соединить, чтобы в конечном итоге получилась трапеция.

Как известно, площадь трапеции равна произведению полусуммы ее оснований на высоту.

Если рассмотреть получившуюся трапецию, как фигуру, состоящую из трех треугольников, то ее площадь можно найти так:

Теперь необходимо уравнять два исходных выражения

О теореме Пифагора и способах ее доказательства можно написать не один том учебного пособия. Но есть ли в нем смысл, когда эти знания нельзя применить на практике?

Практическое применение теоремы Пифагора

К сожалению, в современных школьных программах предусмотрено использование данной теоремы только в геометрических задачах. Выпускники скоро покинут школьные стены, так и не узнав, а как они могут применить свои знания и умения на практике.

На самом же деле использовать теорему Пифагора в своей повседневной жизни может каждый. Причем не только в профессиональной деятельности, но и в обычных домашних делах. Рассмотрим несколько случаев, когда теорема Пифагора и способы ее доказательства могут оказаться крайне необходимыми.

Связь теоремы и астрономии

Казалось бы, как могут быть связаны звезды и треугольники на бумаге. На самом же деле астрономия – это научная сфера, в которой широко используется теорема Пифагора.

Например, рассмотрим движение светового луча в космосе. Известно, что свет движется в обе стороны с одинаковой скоростью. Траекторию АВ, которой движется луч света назовем l. А половину времени, которое необходимо свету, чтобы попасть из точки А в точку Б, назовем t. И скорость луча – c. Получается, что: c*t=l

Если посмотреть на этот самый луч из другой плоскости, например, из космического лайнера, который движется со скоростью v, то при таком наблюдении тел их скорость изменится. При этом даже неподвижные элементы станут двигаться со скоростью v в обратном направлении.

Допустим, комический лайнер плывет вправо. Тогда точки А и В, между которыми мечется луч, станут двигаться влево. Причем, когда луч движется от точки А в точку В, точка А успевает переместиться и, соответственно, свет уже прибудет в новую точку С. Чтобы найти половину расстояния, на которое сместилась точка А, нужно скорость лайнера умножить на половину времени путешествия луча (t’).

А чтобы найти, какое расстояние за это время смог пройти луч света, нужно обозначить половину пути новой буковой s и получить следующее выражение:

Если представить, что точки света С и В, а также космический лайнер – это вершины равнобедренного треугольника, то отрезок от точки А до лайнера разделит его на два прямоугольных треугольника. Поэтому благодаря теореме Пифагора можно найти расстояние, которое смог пройти луч света.

Этот пример, конечно, не самый удачный, так как только единицам может посчастливиться опробовать его на практике. Поэтому рассмотрим более приземленные варианты применения этой теоремы.

Радиус передачи мобильного сигнала

Современную жизнь уже невозможно представить без существования смартфонов. Но много ли было бы от них прока, если бы они не могли соединять абонентов посредством мобильной связи?!

Качество мобильной связи напрямую зависит от того, на какой высоте находиться антенна мобильного оператора. Для того чтобы вычислить, каком расстоянии от мобильной вышки телефон может принимать сигнал, можно применить теорему Пифагора.

Допустим, нужно найти приблизительную высоту стационарной вышки, чтобы она могла распространять сигнал в радиусе 200 километров.

АВ (высота вышки) = х;

ВС (радиус передачи сигнала) = 200 км;

ОС (радиус земного шара) = 6380 км;

Применив теорему Пифагора, выясним, что минимальная высота вышки должна составить 2,3 километра.

Теорема Пифагора в быту

Как ни странно, теорема Пифагора может оказаться полезной даже в бытовых делах, таких как определение высоты шкафа-купе, например. На первый взгляд, нет необходимости использовать такие сложные вычисления, ведь можно просто снять мерки с помощью рулетки. Но многие удивляются, почему в процессе сборки возникают определенные проблемы, если все мерки были сняты более чем точно.

Дело в том, что шкаф-купе собирается в горизонтальном положении и только потом поднимается и устанавливается к стене. Поэтому боковина шкафа в процессе подъема конструкции должна свободно проходить и по высоте, и по диагонали помещения.

Предположим, имеется шкаф-купе глубиной 800 мм. Расстояние от пола до потолка – 2600 мм. Опытный мебельщик скажет, что высота шкафа должна быть на 126 мм меньше, чем высота помещения. Но почему именно на 126 мм? Рассмотрим на примере.

При идеальных габаритах шкафа проверим действие теоремы Пифагора:

АС=√2474 2 +800 2 =2600 мм – все сходится.

Допустим, высота шкафа равна не 2474 мм, а 2505 мм. Тогда:

АС=√2505 2 +√800 2 =2629 мм.

Следовательно, этот шкаф не подойдет для установки в данном помещении. Так как при поднятии его в вертикальное положение можно нанести ущерб его корпусу.

Пожалуй, рассмотрев разные способы доказательства теоремы Пифагора разными учеными, можно сделать вывод, что она более чем правдива. Теперь можно использовать полученную информацию в своей повседневной жизни и быть полностью уверенным, что все расчеты будут не только полезны, но и верны.

Источник

Теорема Пифагора

Содержание:

Доказательства теоремы пифагора методом разложения

Начертим квадрат со стороной длины 7 см (на рис. 10 уменьшен).

Отложим от его вершины на сторонах отрезки и через полученные точки проведем прямые, параллельные сторонам квадрата. Обозначим точку пересечения одной из них со стороной через точку пересечения второй с через и, наконец, точку пересечения прямых и через

Теперь исходный квадрат со стороною 7 см распался на следующие четыре части: квадрат со стороной 3 см, квадрат со стороной 4 см и два равных прямоугольника, смежные стороны которых равны 3 и 4 см. Чтобы найти площадь квадрата в квадратных сантиметрах, нужно, как известно, умножить число, выражающее длину стороны в сантиметрах, само на себя.

• Площадь прямоугольника равна произведению чисел, выражающих длины двух смежных сторон. Рассматривая описанную выше фигуру, мы можем считать ее геометрическим изображением соотношения или (если число 7 заменить суммой 3+4) соотношения Действительно, в результате вычислений в обеих частях равенств получаем 49.

В нашем примере мы брали числа 3, 4, 7, однако этот выбор был совершенно случайным. Мы получили бы тот же самый результат, взяв какие угодно числа и их сумму Наше рассуждение представляет собой не что иное, как геометрическое доказательство хорошо известной формулы

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Геометрическая фигура, которой мы здесь воспользовались для изображения формулы была известна еще Евклиду, а также индусам до начала нашей эры. «Общее правило для увеличения заданного квадрата» выражалось ими не совсем ясно в следующих словах: «Прибавь к двум сторонам то, что охватывается при каждом удлинении, а у вершины — квадрат, который производится соответствующим удлинением».

Начертим еще раз квадрат со стороной 7 см, но теперь разобьем его иначе. Отложим от вершины квадрата на каждой стороне но 3 см в таком порядке, как показано на рис. 11.

Полученные точки соединим последовательно друг с другом. При этом получится четырехугольник и четыре прямоугольных треугольника, вершины прямых углов которых совпадают с вершинами исходного квадрата. Эти треугольники равны по двум сторонам и углу, заключенному между ними (первый признак равенства треугольников).

Возможно вам будут полезны данные страницы:

Таким образом, гипотенузы всех этих треугольников равны, и четырехугольник — ромб. Читатель, вероятно, уже заметил, что на самом деле этот четырехугольник не только ромб, но и квадрат. Действительно, обозначим угол тогда угол оказывается равным (в силу теоремы, утверждающей, что сумма углов треуг

ольника равна ). Вследствие равенства всех четырех треугольников угол равен углу а тогда угол должен быть равен так как три угла с общей вершиной образуют развернутый угол, равный Такое же рассуждение можно было бы провести и для остальных углов ромба, но и приведенного доказательства уже вполне достаточно, так как равносторонний четырехугольник (ромб), имеющий один прямой угол, должен иметь только прямые углы.

Возьмем теперь, вместо частных значений 3 и 4, какие угодно числа а гипотенузу полученного прямоугольного треугольника обозначим через Тогда разбиение квадрата, представленное на рис. 11, выражается следующей формулой: В самом деле, площадь внутреннего квадрата со стороной а площадь каждого из четырех прямоугольных треугольников равна . Последнее равенство можно переписать так:

Пользуясь этим соотношением, можно вычислить гипотенузу с прямоугольного треугольника, зная численные значения его катетов.

Пусть, например, как выше, тогда из последнего равенства имеем: откуда

Свяжем воедино то, что мы узнали в двух последних пунктах. Ограничимся сначала арифметической стороной дела. мы получили формулу (1) а в п. 2 — (2)

Отсюда следует равенство опуская в обеих его частях слагаемое получим (3) В последнем равенстве суть длины катетов, а —длина гипотенузы прямоугольного треугольника, т. е. это не что иное, как теорема Пифагора. К этому «арифметическому» выводу равенства (3) присоединим еще следующее замечание. Формулу (1) знает каждый учащийся, так как это одно из первых равенств, с которыми он встречается в алгебре. Равенство (1) является тождеством, т. е. имеет место при люб ы х значениях Равенство (2), напротив, не является тождеством, так как оно не будет справедливым при произвольных значениях оно представляет собою соотношение, позволяющее, скажем, вычислить с по известным значениям как это было сделано нами выше.

Многим математикам может не понравиться данный нами в п. 3 вывод теоремы Пифагора, поскольку часто избегают смешения геометрических и арифметических методов в одном и том же доказательстве, и теоремы явно геометрического характера стремятся доказывать чисто геометрическим путем*). В элементарной математике это стремление особенно явственно сказывается как раз в учении о площадях.

Площадь рассматривается здесь чисто геометрически, в отрыве от конкретных численных данных. Доказывается, например, что: Два параллелограмма с равными основаниями и равными высотами равновелики; Два треугольника с равными основаниями и равными высотами равновелики. Подобному «геометрическом» подходу к теории измерения площадей, при котором в основу кладется сравнение площадей двух фигур, противостоит «арифметический» подход, при котором измерение площади рассматривается, ио сути дела, как вычислительная операция.

Указанным выше двум предложениям здесь будут соответствовать родственные им «арифметические» теоремы: Площадь параллелограмма равна произведению его основания на высоту; Площадь треугольника равна половине произведения его основания на высоту. Теорему Пифагора также можно сформулировать двояко.

«Геометрически» ее можно выразить так: Квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик сумме квадратов, построенных на его катетах. «Арифметически» она гласит: Если суть числа, выражающие длины катетов, измеренные в одних и тех же единицах длины, а — число, выражающее длину гипотенузы, измеренной в тех же единицах, то числа связаны соотношением

Наряду с «арифметизованным» доказательством теоремы Пифагора, составляющим содержание п. 3, нетрудно дать и «чисто геометрическое» доказательство ее, также 1 г * / / / 3 // Рис. 12. Рис. 13. опирающееся на построения пп. 1 и 2. Если в обоих прямоугольниках рис. 10 провести по одной диагонали, то мы получим фигуру, изображенную на рис. 12.

Вследствие равенства треугольников, фигурирующих на рис. 12 и 13,

сумма площадей квадратов I и II должна быть равна площади квадрата III. Это и есть теорема Пифагора.

Существует целый ряд доказательств теоремы Пифагора, в которых квадраты, построенные на катетах и на гипотенузе, разрезаются так, что каждой части квадрата, построенного на гипотенузе, соответствует часть одного из двух квадратов, построенных на катетах.

Во всех этих случаях для понимания доказательства достаточно одного взгляда на чертеж; рассуждение здесь может быть ограничено единственным словом: «смотри!», как это делалось в сочинениях древних индусских математиков. Следует, однако, заметить, что на самом деле доказательство нельзя считать полным, пока мы не доказали равенства всех соответствующих друг другу частей.

Это почти всегда довольно нетрудно сделать, однако может (особенно при большом числе частей) потребовать довольно продолжительной работы. Мы начнем со сравнительно нового доказательства Энштейна; его преимуществом является то, что здесь в качестве составных частей разложения фигурируют исключительно треугольники. Чтобы разобраться в чертеже (рис. 14),

заметим, что прямая проведена перпендикулярно прямой 6. В учебниках нередко встречается разложение, указанное на рис. 18).

Через центр квадрата, построенного на большем катете, проводим прямые, параллельную и и перпендикулярную гипотенузе. Соответствие частей фигуры хорошо видно из чертежа. Рис. 18 обладает любопытным свойством: здесь соответствующие друг другу части фигуры не только равны, но и «параллельно расположены», т. е. получаются одна из другой при помощи параллельного перенесения. Возможность такого разложения является счастливой случайностью.

В последнее время было, однако, доказано (швейцарскими геометрами Хадвигером и Глюром), что каждые два равновеликих многоугольника можно разбить на части так, чтобы отвечающие друг другу (треугольные или многоугольные!) части в разбиении обеих фигур были равны, и их соответствующие стороны были параллельны. Заметим, что линии, разбивающие квадрат, построенный на большем катете, совсем не обязательно проводить так, чтобы точкой их пересечения являлся центр квадрата.

Проведем через вершины квадрата прямые, параллельные и перпендикулярные гипотенузе, как показано пунктиром на рис. 18; при этом внутри образуется меньший квадрат, любую точку которого (включая точки, лежащие на его сторонах) можно принять за точку . Далее доказательство идет точно так же, как и ранее. Конечно, построенные теперь четырехугольники не будут равны между собой, как это было в том случае, когда точкой пересечения вспомогательных линий служил центр квадрата.

Рассмотрим еще один способ разложения, в котором, как и раньше, удается ограничиться всего 5 частями. Он встречается уже в арабском комментарии к Евклиду, составленном Аннаирици около 900 г. и. э. В немного измененном виде это доказательство снова появляется у Гёпеля в 1824 г. Способ разбиения квадратов, построенных на катетах, ясен из рис. 19,

в котором учтено предложение II и л ь с е н а, касающееся этого доказательства. Что касается разбиения квадрата, построенного на гипотенузе, то нужно лишь иметь в виду, что часть 3 получается следующим образом: на стороне квадрата, построенного на гипотенузе, откладывается гипотенуза прямоугольного треугольника 3, фигурирующего в разбиении квадрата, построенного на большом катете.

Можно вместо этого отложить катет треугольника 3 на продолжении стороны квадрата, построенного на большем катете. Естественность такого разложения очевидна, если сравнить рис. 19 с рис. 7, на котором квадрат, построенный на большем катете, повернут на вокруг этого катета.

Изображенное на рис.20

разложение принадлежит Гутхейлю; для него характерно наглядное расположение отдельных частей, что позволяет сразу видеть, какие упрощения повлечет за собой случай равнобедренного прямоугольного треугольника.

Помимо четырех указанных нами способов разложения существует еще много других (см., например, рис. 21 и 22).

Мы ограничимся лишь перечисленными доказательствами. Остановимся теперь на вопросе о том, какое из всех возможных доказательств с помощью разложения является простейшим. Если при этом не руководствоваться исключительно личным вкусом, то необходимо дать математическое определение понятия «простоты» доказательства; более того, так как мы собираемся эту простоту оценивать, то необходимо будет условиться о «мере» простоты. При этом надо иметь в виду, что и выбор подобной «меры» опять-таки будет субъективен.

«Мерой простоты» может служить, например, число использованных при доказательстве вспомогательных линий, или число частей разбиения, или оба эти числа одновременно. Можно условиться «мерой простоты» доказательства считать число применений теоремы о равенстве треугольников, предполагая при этом, что доказательство проведено полностью, без всяких ссылок на очевидность.

С этой последней точки зрения вопрос по предложению Бернштейна был изучен Брандесом. Найти простейшее доказательство в смысле этого последнего определения означает установить наименьшее число треугольников, на которые можно разложить квадрат, построенный на гипотенузе, так, чтобы каждому из них соответствовал равный ему треугольник в разбиении квадратов, построенных на катетах. В доказательстве Эпштейна, например, таких треугольников 8; в доказательстве, изложенном в п. 6, 5 четырехугольников, следовательно, 10 треугольников; в доказательстве Аннаирици мерой простоты нужно считать число 7. Каково же наименьшее число треугольников, получающихся при таких разложениях?

Возможны ли разложения, в которых оно меньше семи? Брандес доказал, что число 7 в самом деле есть наименьшее, поэтому доказательство Аннаирици следует считать простейшим из всех, выполненных методом разложения. Более сложными являются доказательства Эпштейна и Гутхейля; еще более сложно доказательство.

Теорема Пифагора в системе Евклида

То доказательство теоремы Пифагора, без которого не обходится ни один учебник элементарной геометрии, было приведено Евклидом в его «Началах»; по свидетельству Прокла (Византия), оно придумано самим Евклидом.

Опустим из соединим точки Очевидно, отсюда следует, что треугольники (заштрихованные на рис. 39) равны между собой (по двум сторонам и углу, заключенному между ними). Сравним далее треугольник и прямоугольник они имеют общее основание и равные > высоты, опущенные на это основание (ибо ), следовательно Точно так же квадрат и треугольник имеют общее основание и равные высоты, опущенные на это основание (так как ) значит,

Отсюда и из равенства треугольников вытекает равновеликость прямоугольника и квадрата аналогично доказывается и равновеликость прямоугольника и квадрата А отсюда, наконец, следует, что квадрат равновелик сумме квадратов т. е. теорема Пифагора.)

Теорема Пифагора и учение о подобии

В прямоугольном треугольнике проведем из вершины прямого угла высоту тогда треугольник разобьется на два треугольника, также являющихся прямоугольными (рис. 44).

Полученные треугольники будут подобны друг другу и исходному треугольнику. Это легко доказать, пользуясь первым признаком подобия: Если два угла одного треугольника соответственно равны двум углам дру- Рис. 44. гого, то такие треугольники подобны. В самом деле, сразу видно, что, кроме прямого угла, треугольники имеют общий угол а, а треугольники —общий угол . То, что малые треугольники также подобны друг другу, следует из того, что каждый из них подобен большому треугольнику. Впрочем, это можно установить и непосредственно. Так как в подобных треугольниках соответственные стороны пропорциональны, то из подобия исходного треугольника и треугольника следует или, что то же, Пользуясь терминами теории пропорций, это можно выразить так:

В прямоугольном треугольнике каждый катет есть средняя пропорциональная между гипотенузой и прилежащим к этому катету отрезком гипотенузы.

В терминах теории площадей это равенство выражает факт, который используется в евклидовом доказательстве, а именно: Квадрат, построенный на катете прямоугольного треугольника, равновелик прямоугольнику, стороны которого равны гипотенузе треугольника и отрезку гипотенузы, прилежащему к рассматриваемому катету. Аналогичное равенство, относящееся к другому катету, имеет вид

• Сложив оба равенства, получим Так мы пришли к совсем простому доказательству теоремы Пифагора, основанному на теории подобия. Оно встречается у индуса Басхара (род. в 1114 г. н. э.) и затем у Леонарда Пизанского (в Practica geometriae, 1220 г.); позднее оно вновь было независимо найдено английским математиком Валлисом (1616— 1703, Оксфорд); ныне оно также включается почти во все учебники элементарной геометрии.

Вычисления с помощью пифагорова равенства

При вычислении одних геометрических величин с помощью других на основании равенства Пифагора мы сразу же сталкиваемся с квадратными радикалами. Начнем с одного важного замечания, относящегося к этим радикалам.

Ясно, что такие выражения, как или не могут быть целыми числами. Но не будут ли они дробными? Чтобы сразу же исключить подобное предположение, рассмотрим, например,

Предположим, что где дробь несократима. Возведя обе части равенства в квадрат и освобождаясь от знаменателя, получим откуда следует, что — четное число. Но тогда делится на 4. Сократив обе части на 2, замечаем, что а следовательно, и также четны. Но это противоречит предположению, что дробь несократима.

Присылайте задания в любое время дня и ночи в ➔

Официальный сайт Брильёновой Натальи Валерьевны преподавателя кафедры информатики и электроники Екатеринбургского государственного института.

Все авторские права на размещённые материалы сохранены за правообладателями этих материалов. Любое коммерческое и/или иное использование кроме предварительного ознакомления материалов сайта natalibrilenova.ru запрещено. Публикация и распространение размещённых материалов не преследует за собой коммерческой и/или любой другой выгоды.

Сайт предназначен для облегчения образовательного путешествия студентам очникам и заочникам по вопросам обучения . Наталья Брильёнова не предлагает и не оказывает товары и услуги.

Источник