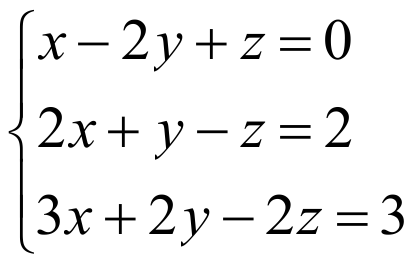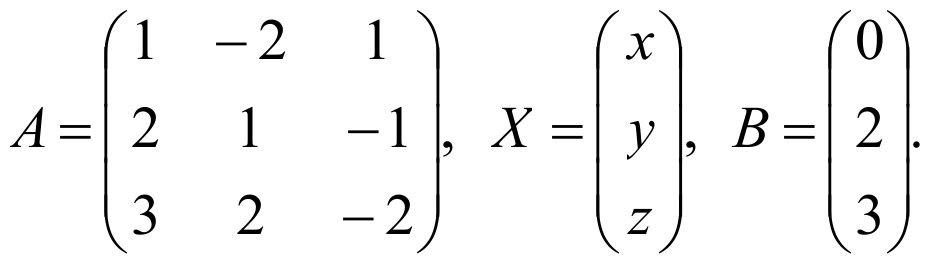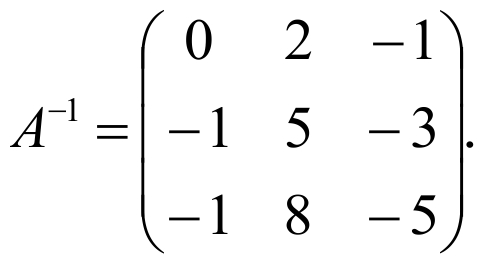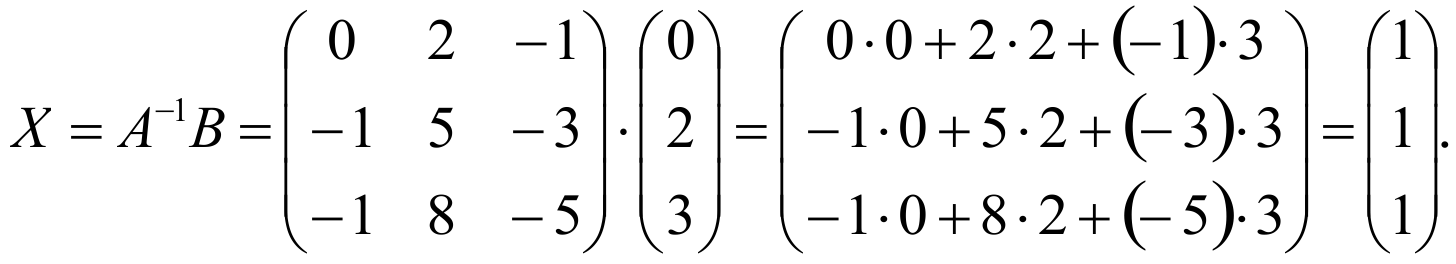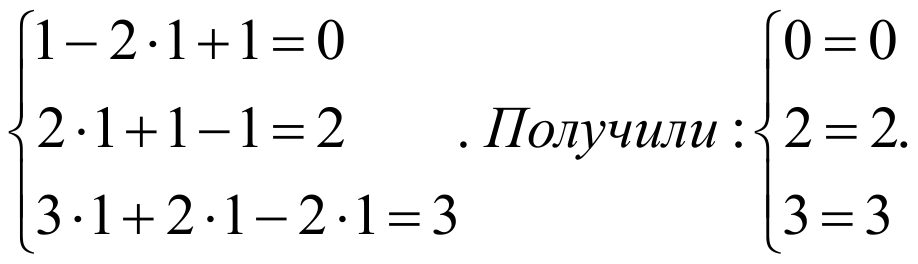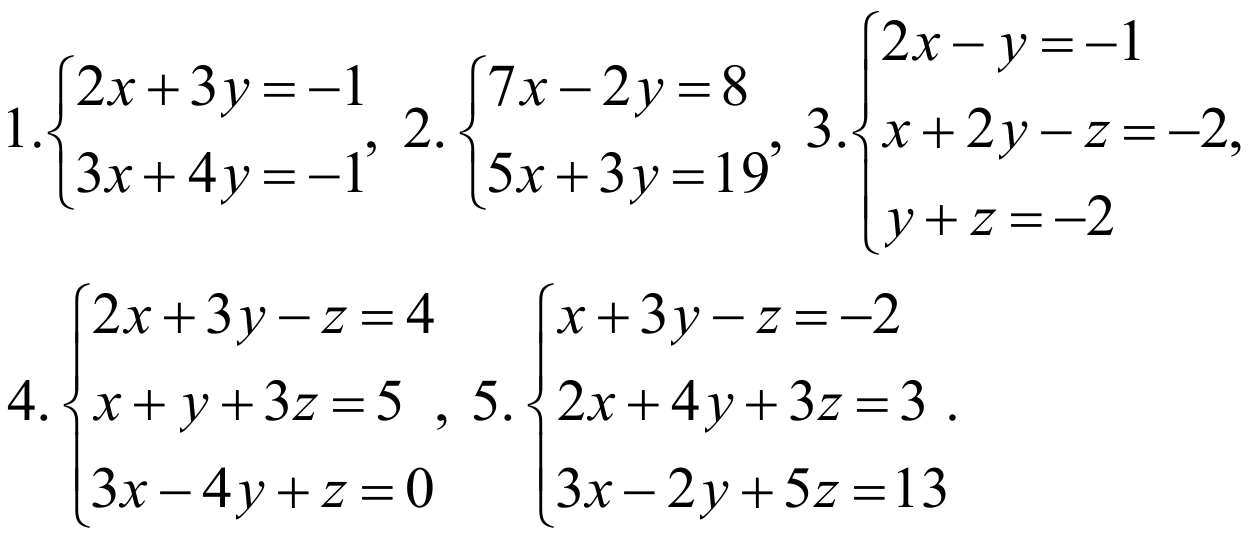Решение слу матричными способами

Матричный метод онлайн

Данный онлайн калькулятор решает систему линейных уравнений матричным методом. Дается очень подробное решение. Для решения системы линейных уравнений выберите количество переменных. Выбирайте метод вычисления обратной матрицы. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить».

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Матричный метод решения систем линейных уравнений

Рассмотрим следующую систему линейных уравнений:

(1)

Для решения системы линейных уравнений (1) матричным методом запишем ее матричном виде:

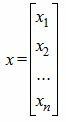(3)

Мы будем предполагать, что матрица A имеет обратное, т.е. определитель матрицы A не равен нулю.

Умножим матричное уравнение (2) на обратную матрицу A −1 . Тогда

A −1 Ax=A −1 b.

(4)

Учитывая определение обратной матрицы, имеем A −1 A=E, где E— единичная матрица. Следовательно (4) можно записать так:

Ex=A −1 b.

(4)

или, учитывая, что Ex=x:

x=A −1 b.

(5)

Таким образом, для решения системы линейных уравнений (1) (или (2)), достаточно умножить обратную к A матрицу на вектор ограничений b.

Примеры решения системы линейных уравнений матричным методом

Пример 1. Решить следующую систему линейных уравнений матричным методом:

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом Жордана-Гаусса. С правой стороны матрицы A запишем единичную матрицу:

.

Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого заменяем местами строки 1 и 2:

.

Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/3,-1/3 соответственно:

.

Выбираем самый большой по модулю ведущий элемент столбца 2. Для этого заменяем местами строки 2 и 3:

.

Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -24/51:

.

Исключим элементы 3-го столбца матрицы выше главной диагонали. Для этого сложим строки 1, 2 со строкой 3, умноженной на 17/53, 85/159 соответственно:

.

Исключим элементы 2-го столбца матрицы выше главной диагонали. Для этого сложим строку 1 со строкой 2, умноженной на -3/17:

.

Делим каждую строку матрицы на ведущий элемент соответствующей строки:

.

Отделяем правую часть матрицы. Полученная матрица является обратной матрицей к A :

.

Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A−1b. Тогда

.

Пример 2. Решить следующую систему линейных уравнений матричным методом:

.

Матричный вид записи системы линейных уравнений: Ax=b, где

.

Найдем обратную к матрице A методом алгебраических дополнений. Вычислим определитель матрицы A :

.

Вычислим все алгебраические дополнения матрицы A:

,

,

,

,

,

,

,

,

.

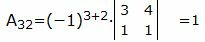Обратная матрица вычисляется из следующего выражения:

где A_ij − алгебраическое дополнение элемента матрицы A, находящиеся на пересечении i-ой строки и j-ого столбца, а Δ − определитель матрицы A.

Используя формулу обратной матрицы, получим:

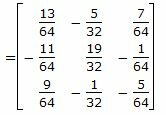Обратная матрица найдена. Решение системы линейных уравнений имеет вид x=A −1 b. Тогда

Источник

ЕГЭ2022 (математика профиль) в ВК

Скоро вебинар
«ПРЯМАЯ НА ПЛОСКОСТИ»
(Аналитическая геометрия). Жми подробнее.

Матричный способ решения СЛУ

«Если Вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.»
Д. Пойа (1887-1985 г.)

(Математик. Внёс большой вклад в популяризацию математики. Написал несколько книг о том, как решают задачи и как надо учить решать задачи.)

Одним из способов решения СЛУ является матричный способ. Этот способ решения СЛУ применим только при выполнении двух условий:

• Число уравнений равно числу неизвестных;
• Определитель матрицы коэффициентов при неизвестных отличен от нуля.

Теорема (матричный способ решения) Пусть дана система n линейных уравнений с n неизвестными, определитель матрицы коэффициентов А которой отличен от нуля. Тогда решение этой системы может быть получено в виде Х=А -1 В, где В – матрица свободных членов, Х— матрица неизвестных.

Запишем матрицу коэффициентов А, матрицу-столбец Х (матрица-столбец неизвестных) и матрицу-столбец В (матрица-столбец свободных членов):

Теперь данную систему можно записать в таком виде АХ=В. Решим это матричное уравнение: Х=А -1 В.

Как найдена матрица А -1 можно посмотреть здесь.

Таким образом, x=1, y=1, z=1.

Подставим в систему вместо x единицу, y единицу и z единицу.

Верно. Записываем ответ.

В открывшемся окне:

• поставить галочку возле «Добавить сообщение получателю»
• в появившемся поле оставить сообщение «в дар» или «подарок».

ИЛИ

оставить комментарий ниже.

Упражнения к уроку:

Решите следующие системы матричным способом:

1. (1;-1); 2. (2,3); 3. (-1,-1,-1); 4. (1,1,1); 5. (2,-1,1).

Автор: Аникина Анна

Комментарии к этой заметке:

Добавить Ваш комментарий

Хотите внести свою лепту в его развитие!? Тогда Вам сюда!

Источник

Онлайн калькулятор. Решение систем линейных уравнений. Матричный метод. Метод обратной матрицы.

Используя этот онлайн калькулятор для решения систем линейных уравнений (СЛУ) матричным методом (методом обратной матрицы), вы сможете очень просто и быстро найти решение системы.

Воспользовавшись онлайн калькулятором для решения систем линейных уравнений матричным методом (методом обратной матрицы), вы получите детальное решение вашей задачи, которое позволит понять алгоритм решения задач на решения систем линейных уравнений, а также закрепить пройденный материал.

Решить систему линейных уравнений матричным методом

Изменить названия переменных в системе

Заполните систему линейных уравнений:

Ввод данных в калькулятор для решения систем линейных уравнений матричным методом

• В онлайн калькулятор вводить можно числа или дроби. Более подробно читайте в правилах ввода чисел.
• Для изменения в уравнении знаков с «+» на «-» вводите отрицательные числа.
• Если в уравнение отсутствует какая-то переменная, то в соответствующем поле ввода калькулятора введите ноль.
• Если в уравнение перед переменной отсутствуют числа, то в соответствующем поле ввода калькулятора введите единицу.

Например, линейное уравнение x ₁ — 7 x ₂ — x ₄ = 2

будет вводится в калькулятор следующим образом:

Дополнительные возможности калькулятора для решения систем линейных уравнений матричным методом

• Между полями для ввода можно перемещаться нажимая клавиши «влево», «вправо», «вверх» и «вниз» на клавиатуре.
• Вместо x ₁, x ₂, . вы можете ввести свои названия переменных.

Вводить можно числа или дроби (-2.4, 5/7, . ). Более подробно читайте в правилах ввода чисел.

Источник

Матричный метод решения СЛАУ: пример решения с помощью обратной матрицы

В данной статье мы расскажем о матричном методе решения системы линейных алгебраических уравнений, найдем его определение и приведем примеры решения.

Метод обратной матрицы — это метод, использующийся при решении СЛАУ в том случае, если число неизвестных равняется числу уравнений.

Найти решение системы n линейных уравнений с n неизвестными:

a 11 x 1 + a 12 x 2 + . . . + a 1 n x n = b 1 a n 1 x 1 + a n 2 x 2 + . . . + a n n x n = b n

Матричный вид записи: А × X = B

где А = а 11 а 12 ⋯ а 1 n а 21 а 22 ⋯ а 2 n ⋯ ⋯ ⋯ ⋯ а n 1 а n 2 ⋯ а n n — матрица системы.

X = x 1 x 2 ⋮ x n — столбец неизвестных,

B = b 1 b 2 ⋮ b n — столбец свободных коэффициентов.

Из уравнения, которое мы получили, необходимо выразить X . Для этого нужно умножить обе части матричного уравнения слева на A — 1 :

A — 1 × A × X = A — 1 × B .

Так как А — 1 × А = Е , то Е × X = А — 1 × В или X = А — 1 × В .

Обратная матрица к матрице А имеет право на существование только, если выполняется условие d e t A н е р а в е н н у л ю . Поэтому при решении СЛАУ методом обратной матрицы, в первую очередь находится d e t А .

В том случае, если d e t A н е р а в е н н у л ю , у системы имеется только один вариант решения: при помощи метода обратной матрицы. Если d e t А = 0 , то систему нельзя решить данным методом.

Пример решения системы линейных уравнений с помощью метода обратной матрицы

Решаем СЛАУ методом обратной матрицы:

2 x 1 — 4 x 2 + 3 x 3 = 1 x 1 — 2 x 2 + 4 x 3 = 3 3 x 1 — x 2 + 5 x 3 = 2

• Записываем систему в виде матричного уравнения А X = B , где

А = 2 — 4 3 1 — 2 4 3 — 1 5 , X = x 1 x 2 x 3 , B = 1 3 2 .

• Выражаем из этого уравнения X :

• Находим определитель матрицы А :

d e t A = 2 — 4 3 1 — 2 4 3 — 1 5 = 2 × ( — 2 ) × 5 + 3 × ( — 4 ) × 4 + 3 × ( — 1 ) × 1 — 3 × ( — 2 ) × 3 — — 1 × ( — 4 ) × 5 — 2 × 4 — ( — 1 ) = — 20 — 48 — 3 + 18 + 20 + 8 = — 25

d e t А не равняется 0, следовательно, для этой системы подходит метод решения обратной матрицей.

• Находим обратную матрицу А — 1 при помощи союзной матрицы. Вычисляем алгебраические дополнения А i j к соответствующим элементам матрицы А :

А 11 = ( — 1 ) ( 1 + 1 ) — 2 4 — 1 5 = — 10 + 4 = — 6 ,

А 12 = ( — 1 ) 1 + 2 1 4 3 5 = — ( 5 — 12 ) = 7 ,

А 13 = ( — 1 ) 1 + 3 1 — 2 3 — 1 = — 1 + 6 = 5 ,

А 21 = ( — 1 ) 2 + 1 — 4 3 — 1 5 = — ( — 20 + 3 ) = 17 ,

А 22 = ( — 1 ) 2 + 2 2 3 3 5 — 10 — 9 = 1 ,

А 23 = ( — 1 ) 2 + 3 2 — 4 3 — 1 = — ( — 2 + 12 ) = — 10 ,

А 31 = ( — 1 ) 3 + 1 — 4 3 — 2 4 = — 16 + 6 = — 10 ,

А 32 = ( — 1 ) 3 + 2 2 3 1 4 = — ( 8 — 3 ) = — 5 ,

А 33 = ( — 1 ) 3 + 3 2 — 4 1 — 2 = — 4 + 4 = 0 .

• Записываем союзную матрицу А * , которая составлена из алгебраических дополнений матрицы А :

А * = — 6 7 5 17 1 — 10 — 10 — 5 0

• Записываем обратную матрицу согласно формуле:

A — 1 = 1 d e t A ( A * ) T : А — 1 = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 ,

• Умножаем обратную матрицу А — 1 на столбец свободных членов В и получаем решение системы:

X = A — 1 × B = — 1 25 — 6 17 — 10 7 1 — 5 5 — 10 0 1 3 2 = — 1 25 — 6 + 51 — 20 7 + 3 — 10 5 — 30 + 0 = — 1 0 1

Ответ: x 1 = — 1 ; x 2 = 0 ; x 3 = 1

Источник