Решение системы при различных способах выбора базиса

Метод Жордана-Гаусса онлайн

Данный онлайн калькулятор находит общее решение системы линейных уравнений методом Жордана-Гаусса. Дается подробное решение. Для вычисления выбирайте количество уравнений и количество переменных. Затем введите данные в ячейки и нажимайте на кнопку «Вычислить.» Теоретическую часть нахождения решения системы линейных уравнений методом Жордана-Гаусса смотрите ниже.

Предупреждение

Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b (b>0) целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.

Метод Жордана-Гаусса

Метод Жордана-Гаусса − это метод для решения систем линейных уравнений а также метод нахождения обратной матрицы. Данный метод является модификацией метода Гаусса.

Первый этап метода Жордана-Гаусса аналогична методу Гаусса (прямой ход Гаусса), который подробно можно посмотреть на странице «Метод Гаусса онлайн». Второй этап (обратный ход) метода Жордана-Гаусса заключается в обнулении всех элементов матрицы коэффициентов системы линейных уравнений, выше ведущих элементов. Отметим, что мы здесь рассматриваем произвольную систему линейных уравнений, где число переменных может быть не равным числу ограничений.

Рассмотрим следующую систему линейных уравнений:

(1)

Запишем систему (1) в матричном виде:

(3)

A-называется матрица коэффициентов системы, b − правая часть ограничений, x− вектор переменных, которую нужно найти. Пусть rang(A)=p.

Построим расшренную матрицу системы:

(4)

После прямого хода Гаусса (подробнее о прямом ходе Гаусса посмотрите на странице «Метод Гаусса онлайн») получим следующую расширенную матрицу:

(5)

Если . равны нулю, то система линейных уравнений имеет решение, если же хотя бы один из этих чисел отлично от нуля, то система несовместна. Иными словами, система (2) совместна тогда и только тогда, когда ранг матрицы A навен рангу расширенной матрицы (A|b).

Пусть . Тогда в обратном порядке, начиная с ведущего элемента применяем обратный ход Гаусса. Суть обратного хода заключается в обнулении всех элементов расширенной матрицы, стоящих выше ведущих элементов.

Итак, обнуляем все элементы, стоящие в столбце p, выше элемента . Так как ≠0, то сложим строки 1,2. p−1 со строкой p, умноженной на соответственно.

Расширенная матрица примет следующий вид:

Аналогичным методом обнуляем элементы столбцов p−1, p−2, . 2 выше ведущих элементов .

Расширенная матрица примет следующий вид:

Делим каждую строку на соответствующий ведущий элемент (если ведущий элемент существует):

Тогда решение можно записать так:

где − произвольные вещественные числа.

Отметим, что при m=n и rangA=n система линейных уравнений (2) имеет единственное решение.

Рассмотрим численные примеры.

Примеры решения системы линейных уравнений методом Жордана-Гаусса

Пример 1. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где

.

Для решения системы, построим расширенную матрицу:

.

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на 1/2,-3/2 соответственно:

.

Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на 1/5:

.

Второй этап. Обратный ход Гаусса

Исключим элементы 3-го столбца матрицы выше элемента a₃₃. Для этого сложим строки 1, 2 со строкой 3, умноженной на -3/2, -5/4 соответственно:

.

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на -2/5:

.

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

.

.

Векторный вариант решения:

.

Пример 2. Найти решение системы линейных уравнений методом Жордана-Гаусса:

Матричный вид записи: Ax=b, где

Для решения системы, построим расширенную матрицу:

Обозначим через a_ij элементы i-ой строки и j-ого столбца.

Первый этап. Прямой ход Гаусса.

Исключим элементы 1-го столбца матрицы ниже элемента a₁₁. Для этого сложим строки 2,3 со строкой 1, умноженной на 4/3, 5/3 соответственно:

Исключим элементы 2-го столбца матрицы ниже элемента a2 2. Для этого сложим строку 3 со строкой 2, умноженной на -2:

Второй этап. Обратный ход Гаусса

Исключим элементы 2-го столбца матрицы выше элемента a₂₂. Для этого сложим строку 1 со строкой 2, умноженной на -3/10:

Делим каждую строку матрицы на соответствующий ведущий элемент (если ведущий элемент существует):

Выразим переменные x₁, x₂ относительно остальных переменных.

x₃− произвольное действительное число.

Векторный вариант решения:

Запишем вышеизложенное решение, представив свободные переменные в виде тождеств:

Тогда векторное решение можно представить так:

,

x₃− произвольное действительное число.

Источник

Решение системы при различных способах выбора базиса

Решение произвольных систем

Пусть дана система m линейных уравнений с n неизвестными:

(1)

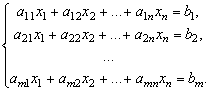
В матричной форме система (1) имеет вид

где А = — матрица коэффициентов системы;

Х = — матрица-столбец переменных;

В = — матрица-столбец свободных членов.

Решением системы (1) называется всякий вектор 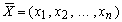, координаты которого обращают каждое уравнение системы в верное равенство.

Система уравнений, имеющая хотя бы одно решение, называется совместной. Система уравнений называется несовместной, если она не имеет ни одного решения.

Система уравнений называется определенной, если она имеет единственное решение, и неопределенной, если она имеет более одного решения.

Две системы называются эквивалентными, если множества их решений совпадают.

Теорема 1. (теорема Кронекера — Капелли ). Система (1) совместна тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы системы:

.

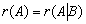
Теорема 2 . Если ранг матрицы совместной системы равен числу неизвестных, то система имеет единственное решение. Если ранг матрицы совместной системы меньше числа неизвестных, то система имеет бесконечно много решений.

Пусть ранг матрицы r ( A )= r n . Переменные называются базисными (основными), если определитель матрицы коэффициентов при них (базисный минор) отличен от нуля. Количество базисных переменных равно r . Другие n — r переменных называются свободными ( неосновными ). Выражение базисных переменных через свободные называется общим решением системы. Из него можно получить бесконечное множество частных решений, придавая свободным переменным произвольные значения.

Решение системы (1), в котором свободные переменные имеют нулевые значения, называется базисным решением. Число различных базисных решений не превосходит .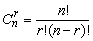

Метод последовательного исключения неизвестных

Метод Гаусса — это универсальный метод исследования и решения произвольных систем линейных уравнений. Он состоит в приведении системы к диагональному виду путем последовательного исключения неизвестных с помощью элементарных преобразований, не нарушающих эквивалентности систем. Переменная считается исключенной, если она содержится только в одном уравнении системы с коэффициентом 1.

Элементарными преобразованиями системы являются:

— умножение уравнения на число, отличное от нуля;

— сложение уравнения, умноженного на любое число, с другим уравнением;

— отбрасывание уравнения 0 = 0.

Если при выполнении элементарных преобразований получено уравнение вида 0 = k (где k 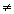0), то система несовместна.

Перейдем теперь к решению систем с различным количеством неизвестных и уравнений. Пусть дана система m линейных уравнений с n неизвестными. Если такая система совместна, то при r n она имеет бесконечное множество решений, каждое из которых может быть получено из общего решения системы.

Для нахождения общего решения нам необходимо выбрать, какие неизвестные мы будем считать основными (базисными). Это могут быть любые r переменных, коэффициенты при которых составляют определитель, отличный от нуля. Затем выбранные основные переменные нужно выразить через свободные. Для этого с помощью элементарных преобразований необходимо расширенную матрицу системы привести к такому виду, чтобы коэффициенты при базисных переменных образовали так называемые базисные столбцы — столбцы, состоящие из нулей и одной единицы.

Решение систем линейных уравнений методом последовательного исключения неизвестных можно оформлять в виде таблицы.

Левый столбец таблицы содержит информацию об исключенных (базисных) переменных. Остальные столбцы содержат коэффициенты при неизвестных и свободные члены уравнений.

В исходную таблицу записывают расширенную матрицу системы. Далее приступают к выполнению очередной итерации:

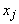
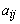
1. Выбирают переменную , которая войдет в число базисных , и уравнение, в котором эта переменная останется. Соответствующие столбец и строку таблицы называют ключевыми. Коэффициент , стоящий на пересечении ключевой строки и ключевого столбца, называют ключевым.

2. Элементы ключевой строки делят на ключевой элемент.

3. Ключевой столбец заполняют нулями.

4. Остальные элементы вычисляют по правилу прямоугольника: составляют прямоугольник, в противоположных вершинах которого находятся ключевой элемент и пересчитываемый элемент; из произведения элементов, стоящих на диагонали прямоугольника с ключевым элементом, вычитают произведение элементов другой диагонали и полученную разность делят на ключевой элемент.

Переход к другому базису

Перейти от одного базиса системы к другому позволяет преобразование однократного замещения: вместо одной из основных переменных в базис вводят одну из свободных переменных. Для этого в столбце свободной переменной выбирают ключевой элемент и выполняют преобразования по указанному выше алгоритму, начиная с п. 2.

Нахождение опорных решений

Опорным решением системы линейных уравнений называется базисное решение, не содержащее отрицательных компонент.

Опорные решения системы находят методом Гаусса при выполнении следующих условий.

1. В исходной системе все свободные члены должны быть неотрицательны: .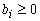

2. В число базисных может быть введена только та переменная, в столбце коэффициентов при которой есть хотя бы один положительный элемент.

3. Если при переменной, вводимой в базис, имеются положительные коэффициенты в нескольких уравнениях, то переменная вводится в базис в то уравнение, которому соответствует наименьшее в столбце отношение свободных членов к этим положительным коэффициентам.

Замечание 1 . Если в процессе исключения неизвестных появится уравнение, в котором все коэффициенты неположительны , а свободный член 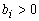, то система не имеет неотрицательных решений.

Замечание 2 . Если в столбцах коэффициентов при свободных переменных нет ни одного положительного элемента, то переход к новому опорному решению невозможен.

Источник