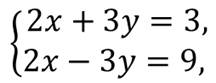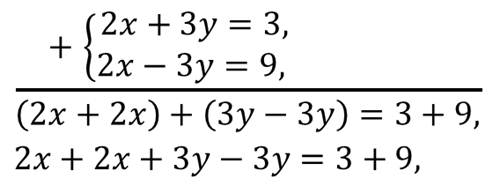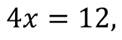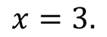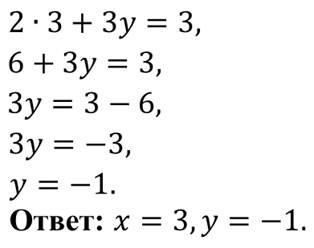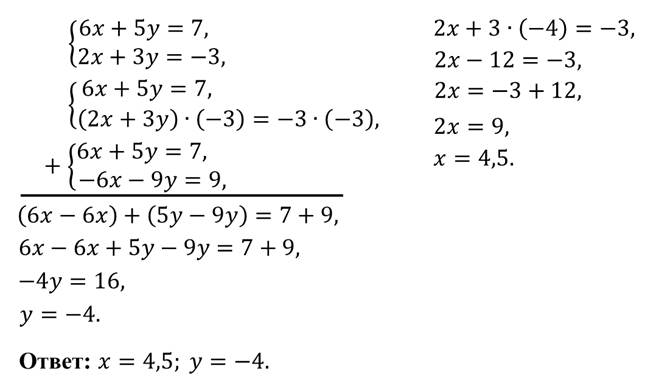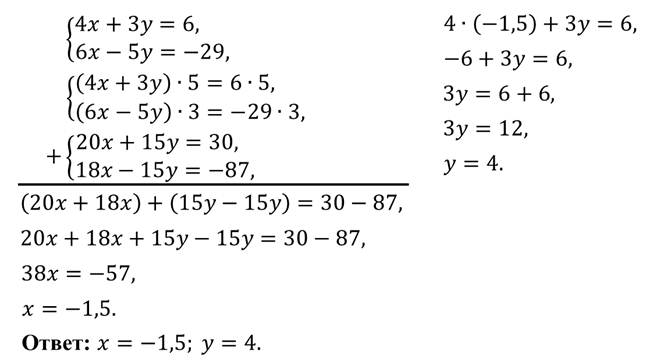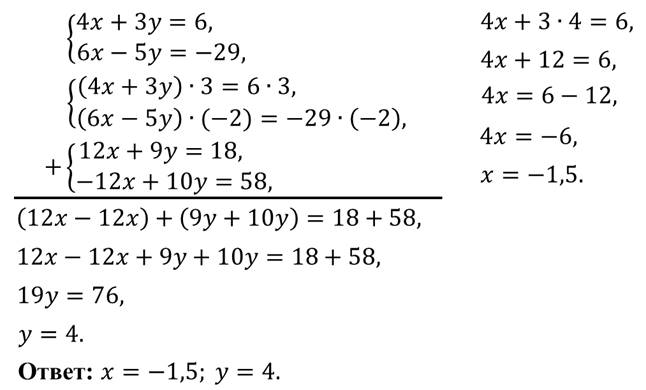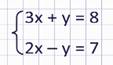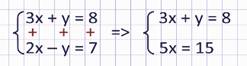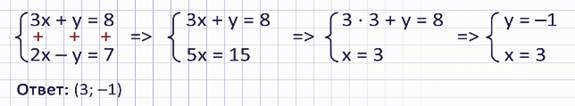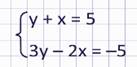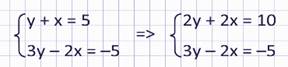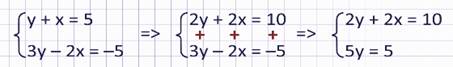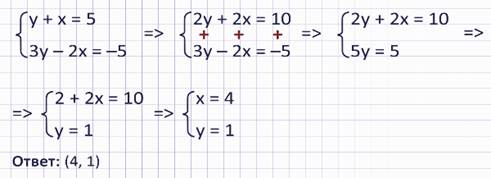Решение систем способом сложения видеоурок

Решение систем линейных уравнений способом сложения

Урок 43. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом сложения»

· показать еще один способ решения систем линейных уравнений – способ сложения.

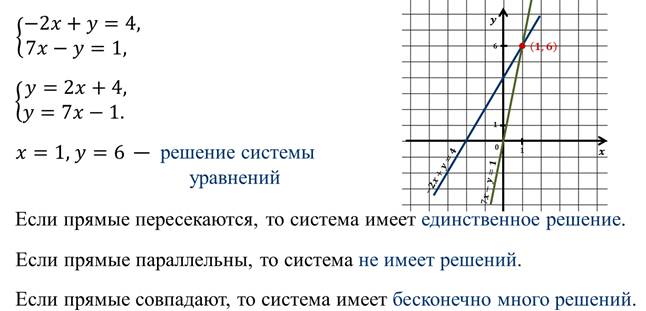
Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.

На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.

Рассмотрим следующую систему

Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений

Приведём подобные слагаемые в обеих частях получившегося уравнения

Видим, что получили уравнение с одной переменной.

Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.

Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.

Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:

1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений системы;

3) решить получившееся уравнение с одной переменной;

4) найти соответствующее значение второй переменной.

При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.

Источник

Решение систем способом сложения видеоурок

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

• Главная
• 7-Класс
• Алгебра
• Видеоурок «Метод алгебраического сложения»

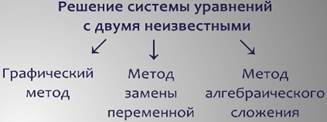
Решить систему уравнений с двумя неизвестными можно различными способами – графическим методом или методом замены переменной.

В этом уроке познакомимся с ещё одним способом решения систем, который Вам наверняка понравится – это способ алгебраического сложения.

А откуда вообще взялась идея – что-то складывать в системах? При решении систем главной проблемой является наличие двух переменных, ведь решать уравнения с двумя переменными мы не умеем. Значит, надо каким-либо законным способом исключить одну из них. И такими законными способами являются математические правила и свойства.

Одно из таких свойств звучит так: сумма противоположных чисел равна нулю. Значит, если при одной из переменных будут противоположные коэффициенты, то их сумма будет равна нулю и нам удастся исключить эту переменную из уравнения. Понятно, что складывать только слагаемые с нужной нам переменной мы не имеем право. Складывать надо уравнения целиком, т.е. по отдельности складывают подобные слагаемые в левой части, затем в правой. В результате мы получим новое уравнение, содержащее только одну переменную. Давайте рассмотрим сказанное на конкретных примерах.

Решить методом алгебраического сложения систему уравнений

Мы видим, что в первом уравнении есть переменная у, а во втором противоположное число –у. Значит, это уравнение можно решить методом сложения.

Одно из уравнений оставляют в том виде, каком оно есть. Любое, какое Вам больше нравится.

А вот второе уравнение будет получено сложением этих двух уравнений почленно. Т.е. 3х сложим с 2х, у сложим с –у, 8 сложим с 7.

Получим систему уравнений

Второе уравнение этой системы представляет собой простое уравнение с одной переменной. Из него находим х = 3. Подставив найденное значение в первое уравнение, находим у = –1.

Решить методом алгебраического сложения систему уравнений

В данной системе нет переменных с противоположными коэффициентами. Но мы знаем, что обе части уравнения можно умножать на одно и то же число. Давайте умножим первое уравнение системы на 2.

Тогда первое уравнение примет вид:

Теперь видим, что при переменной х есть противоположные коэффициенты. Значит, поступим так же, как и в первом примере: одно из уравнений оставим в неизменном виде. Например, 2у + 2х = 10. А второе получим сложением.

Теперь у нас система уравнений:

Легко находим из второго уравнения у = 1, а затем из первого уравнения х = 4.

Давайте подведём итоги:

Мы научились решать системы двух линейных уравнений с двумя неизвестными методом алгебраического сложения. Таким образом, нам теперь известны три основных метода решения таких систем: графический, метод замены переменной и метод сложения. Практически любую систему можно решить с помощью этих способов. В более сложных случаях применяют комбинацию этих приёмов.

Источник

Решение систем линейных уравнений способом сложения

Урок 43. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом сложения»

· показать еще один способ решения систем линейных уравнений – способ сложения.

Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.

На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.

Рассмотрим следующую систему

Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений

Приведём подобные слагаемые в обеих частях получившегося уравнения

Видим, что получили уравнение с одной переменной.

Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.

Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.

Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:

1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений системы;

3) решить получившееся уравнение с одной переменной;

4) найти соответствующее значение второй переменной.

При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.

Источник

Решение систем линейных уравнений способом сложения

Урок 43. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом сложения»

· показать еще один способ решения систем линейных уравнений – способ сложения.

Мы с вами уже познакомились с двумя способами решения систем линейных уравнений с двумя переменными, а именно, с графическим способом и способом подстановки.

На этом уроке мы познакомимся с ещё одним способом решения систем линейных уравнений, который называют способом сложения.

Рассмотрим следующую систему

Обратите внимание, что в уравнениях системы коэффициенты при переменной игрек – противоположные числа. Сложим почленно левые и правые части уравнений

Приведём подобные слагаемые в обеих частях получившегося уравнения

Видим, что получили уравнение с одной переменной.

Затем, чтобы найти значение переменной игрек, мы подставим х = 3 в любое уравнение системы, например, в первое. Снова получили уравнение с одной переменной у. Решим его.

Убедиться в этом вы можете, подставив эти значения в каждое уравнение системы.

Можем сделать вывод: чтобы решить систему линейных уравнений способом сложения, надо:

1) умножить почленно уравнения системы, подбирая множители так, чтобы коэффициенты при одной из переменных стали противоположными числами;

2) сложить почленно левые и правые части уравнений системы;

3) решить получившееся уравнение с одной переменной;

4) найти соответствующее значение второй переменной.

При этом следует помнить, что если коэффициенты при одной из переменных являются противоположными числами, то решение системы сразу начинают с почленного сложения уравнений.

Источник