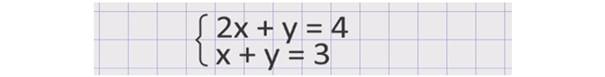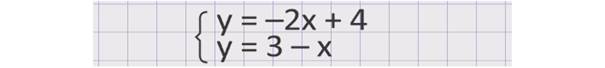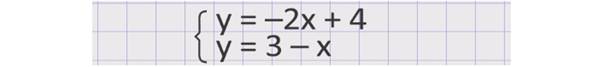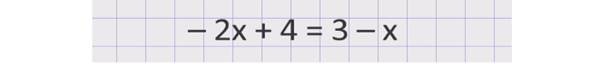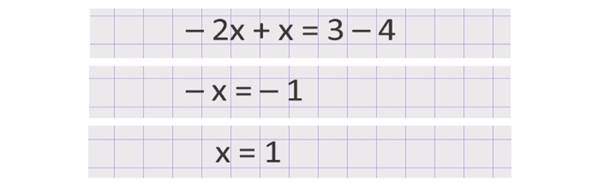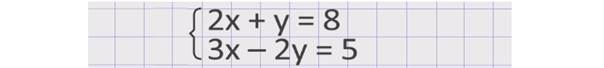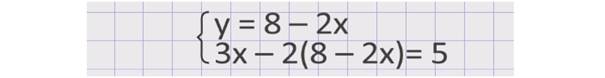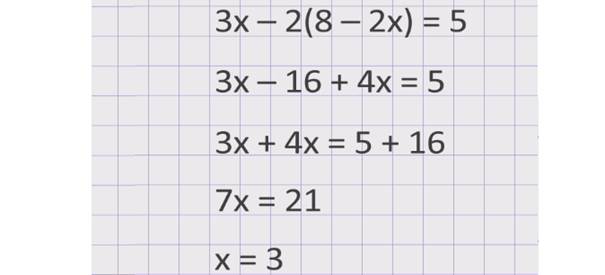Решение систем рациональных уравнений способом подстановки 8 класс никольский видеоурок

Письмо с инструкцией по восстановлению пароля
будет отправлено на вашу почту

Главная
7-Класс
Алгебра
Видеоурок «Решение систем уравнений методом подстановки»

Вспомним, что такое система уравнений.

Система двух уравнений с двумя переменными – это записанные друг под другом два уравнения, объединённые фигурной скобкой. Решить систему – это значит найти такую пару чисел, которая будет являться решением и первого, и второго уравнения одновременно.

В этом уроке познакомимся с таким способом решения систем, как способподстановки.

Давайте рассмотрим систему уравнений:

Можно решить эту систему графически. Для этого нам надо будет построить в одной системе координат графики каждого из уравнений, преобразовав их к виду:

Затем найти координаты точки пересечения графиков, которые и будут являться решением системы. Но графический способ далеко не всегда удобен, т.к. отличается малой точностью, а то и вовсе недоступностью. Попробуем рассмотреть нашу систему повнимательнее. Теперь она имеет вид:

Можно заметить, что левые части уравнений равны, а значит, должны быть равны и правые. Тогда мы получим уравнение:

Это знакомое нам уравнение с одной переменной, которое мы решать умеем. Перенесём неизвестные слагаемые в левую часть, а известные – в правую, не забыв поменять знаки +,– при переносе. Получим:

Теперь подставим найденное значение х в любое уравнение системы и найдём значение у. В нашей системе удобнее использовать второе уравнение у = 3 – х, после подстановки получим у = 2. А теперь проанализируем выполненную работу. Сначала мы в первом уравнении выразили переменную у через переменную х. Затем полученное выражение – 2х + 4 подставили во второе уравнение вместо переменной у. Потом решили полученное уравнение с одной переменной х и нашли ее значение. И в заключении использовали найденное значение х для нахождения другой переменной у. Тут возникает вопрос: а обязательно ли было выражать переменную у из обоих уравнений сразу? Конечно нет. Мы могли выразить одну переменную через другую только в одном уравнении системы и использовать его вместо соответствующей переменной во втором. Причём выразить можно любую переменную из любого уравнения. Здесь выбор зависит исключительно из удобства счёта. Подобный порядок действий математики назвали алгоритмом решения систем двух уравнений с двумя переменными методом подстановки.Вот как он выглядит.

1.Выразить одну из переменных через другую в одном из уравнений системы.

2.Подставить полученное выражение вместо соответствующей переменной в другое уравнение системы.

3.Решить полученное уравнение с одной переменной.

4.Найденное значение переменной подставить в выражение, полученное в пункте первом, и найти значение другой переменной.

5.Записать ответ в виде пары чисел, которые были найдены на третьем и четвертом шаге.

Давайте рассмотрим ещё один пример. Решить систему уравнений:

Здесь удобнее выразить переменную у из первого уравнения. Получим у = 8 – 2х. Полученное выражение надо подставить вместо у во второе уравнение. Получим:

Выпишем это уравнение отдельно и решим его. Сначала раскроем скобки. Получим уравнение 3х – 16 + 4х = 5. Соберём неизвестные слагаемые в левой части уравнения, а известные — в правой и приведём подобные слагаемые. Получим уравнение 7х = 21, отсюда х = 3.

Теперь, используя найденное значение х, можно найти:

Ответ: пара чисел (3; 2).

Таким образом, на этом уроке мы научились решать системы уравнений с двумя неизвестными аналитическим, точным способом, не прибегая к сомнительному графическому.

Источник

Решение систем рациональных уравнений способом подстановки 8 класс никольский видеоурок

Если Вы не нашли темы для своего учебника, то можете добавить оглавление учебника и получить благодарность от проекта «Инфоурок».

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

В Минпросвещения предложили организовать телемосты для школьников России и Узбекистана

Время чтения: 1 минута

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Российские школьники завоевали пять медалей на олимпиаде по физике

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

Шойгу предложил включить географию в число вступительных экзаменов в вузы

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Источник

Решение систем рациональных уравнений способом подстановки 8 класс никольский видеоурок

Безлимитный доступ к занятиям с онлайн-репетиторами

Выгоднее, чем оплачивать каждое занятие отдельно

Вопрос о QR-кодах для сотрудников школ пока не обсуждается

Время чтения: 2 минуты

Минпросвещения разрабатывает образовательный минимум для подготовки педагогов

Время чтения: 2 минуты

Минпросвещения будет стремиться к унификации школьных учебников в России

Время чтения: 1 минута

Студентам вузов могут разрешить проходить практику у ИП

Время чтения: 1 минута

Рособрнадзор откажется от ОС Windows при проведении ЕГЭ до конца 2024 года

Время чтения: 1 минута

В Осетии студенты проведут уроки вместо учителей старше 60 лет

Время чтения: 1 минута

Подарочные сертификаты

Источник

План-конспект урока по алгебре 8 класс по теме:» Решение систем уравнения способом подстановки.»

Образовательное учреждение: МБОУ СОШ №2 г. Батайск Ростовской обл.

Учитель: Васенина Татьяна Викторовна, учитель математики высшей квалификационной категории.

УМК : «Алгебра. 8 класс».

Авторы УМК: Георгий Константинович Муравин – кандидат педагогических наук, Ольга Викторовна Муравина – кандидат педагогических наук, доцент.

Научное консультирование: Зевина Л. В. – научный руководитель областных экспериментальных и пилотных площадок по апробации данных УМК в школах Ростовской области, кандидат педагогических наук, доцент, Master of education , заведующий кафедрой математики и естественных дисциплин РО РИПК и ППРО.

Тема урока : Решение системы уравнений способом подстановки.

Тип урока: урок «открытия» знания.

Оборудование: УМК «Алгебра. 8 класс» авторов Муравина Г.К. и Муравиной О.В., сигнальные карточки, мультимедиа-проектор.

Цель урока : организация продуктивной деятельности школьников, направленной на достижение ими следующих результатов:

способности иметь собственное мнение;

умения учиться самостоятельно;

умения хорошо говорить и легко выражать свои мысли;

опыта применения своих знаний и умений к решению новых проблем;

умения уверенно и легко выполнять математические операции;

способности преодолевать интеллектуальные трудности, решать принципиально новые задачи, проявлять уважение к интеллектуальному труду и его результатам;

позитивных эмоций от математической деятельности, в том числе от нахождения ошибки в своих построениях, как источника улучшения и нового понимания.

освоение способов деятельности:

комбинирование известных алгоритмов деятельности в ситуациях, не предполагающих стандартное применение одного из них;

определение адекватных способов решения учебной задачи на основании заданных алгоритмов;

сравнение, сопоставление, классификация, ранжирование объектов по одному или нескольким признакам;

умение разделять процессы на этапы, звенья;

-способность к логическому рассуждению и коммуникации, ее использование и понимание ее ценности;

умение вступать в речевое общение, участвовать в диалоге;

составление плана, тезиса, конспекта;

развитие умений анализировать, аргументировать сделанный выбор;

приведение примеров, подбор аргументов, формулирование выводов;

отражение в устной и письменной форме результатов своей деятельности.

поиск и устранение причин возникших трудностей;

оценивание своих учебных достижений;

работать в группах и индивидуально;

умение ставить личностные цели и оценивать степень их достижения;

— понимание смысла понятия «системы двух уравнений с двумя переменными», «решение системы двух уравнений с двумя переменными»;

— умение правильно употреблять термины «система»; «решение системы»; понимать их в тексте, в речи учителя и одноклассника, понимать формулировку задания: «решить систему»;

-понимание сути способов подстановки и сложения для решения систем уравнений с двумя переменными;

— осознанное употребление нового математического понятия «подстановка» в устной и письменной речи;

-приобретение опыта использования имеющихся знаний и опыта математической деятельности (например, решение системы; способ сложения для решения линейных систем с двумя переменными; равносильные преобразования систем; решение квадратных и линейных уравнений различными способами);

-умение «открывать» новое знание: новый способ решения систем уравнений — способ подстановки;

— умение делать проверку и оценивать полученные результаты решения задач;

-умение оценивать результаты своей деятельности в соответствии с поставленными целями;

— умение решать системы уравнений с двумя переменными, в которых одно уравнение второй степени.

Организационно — мотивационный этап (3 мин)

Здравствуйте ребята! Я рада видеть вас!

За окном весна! Красиво, светит солнышко. Тепло и уютно! Думаю, что сегодня и на уроке будет всем комфортно, отношения будут теплые и доверительные. Не бойтесь сделать ошибку! Ведь ошибка — источник опыта! Все будет хорошо. На сегодняшнем уроке у нас присутствуют гости.

Договоримся о правилах работы на уроке.

Обратная связь на уроке осуществляется при помощи сигнальных карточек красного и зеленого цветов. Напомню, зеленый цвет означает «У меня такое же мнение (или ответ)», а красный – «иное мнение (или иной ответ)». В случае расхождения мнений идет обсуждение, выявляется причина разногласия. Приготовьте свои сигнальные карточки.

Этап постановки личностных целей (2 мин.)

Ребята, а задумывался ли каждый из вас над тем, с какой целью он сегодня пришел в школу? Какая цель есть у каждого из вас?

Я вам постараюсь помочь вам найти свою цель.

На экране вы видите список личностных целей ( Слайд № 1)

В список личностных целей, который почти повторяет перечень личностных результатов, прописанных в цели, есть смысл добавить последнюю (№8), чтобы проверить, сколько детей выберут только эту цель. Диагностика ценностных ориентиров учащихся с помощью выбора целей поможет организовать работу по проблеме формирования мотивационной сферы и ценностных ориентиров восьмиклассников, чтобы оказывать влияние на формирующиеся приоритеты, ценностные установки и мотивы подростков.

Учитель предлагает одному из учеников класса прочитать все цели вслух.

— Выберите из этого списка для себя одну или несколько формулировок целей и запишите их номер на полях. Постарайтесь поработать на эту цель в течение всего урока. В конце урока проанализируем, были ли они вами достигнуты.

На экране записано квадратное уравнение 15х 2 + 4х + 2015 = 0 (Слайд № 2)

Ребята дайте название объекта, записанного на доске.

Возможные ответы : многочлен, равный нулю; уравнение; квадратный трехчлен, равный нулю; квадратное уравнение. Старший коэффициент равен 15, второй коэффициент 4 и свободный член 2015. Может в записи квадратного уравнения есть нужная нам информация? Учитель последовательно записывает ответы детей на доске.

Учащиеся могут догадаться, что коэффициенты квадратного уравнения подсказывают дату проведения урока (Слайд № 3,4)

— Запишите в тетрадях дату: 15 . 04.2015 и слова: «Классная работа».

— Выдающийся французский математик, физик Рене Декарт утверждал: «Для того чтобы усовершенствовать ум, надо больше размышлять, чем заучивать». Сегодня предлагаю вам попытаться прочувствовать, что переживали великие, открывая новые знания. Сегодняшний урок – урок «открытия» нового знания. Верю, что у вас все получится! (Слайд № 5)

3.Этап актуализации знаний (5 мин)

3.1. Фронтальная работа

Приём 1. «Урок без темы» (впервые на областном мастер-классе этот прием использовала учитель математики МБУ Вильямсская СОШ №3 Кагальницкого района Татьяна Николаевна Тарасова)

Описание приема: универсальный приём ТРИЗ направлен на создание внешней мотивации изучения темы урока. Данный прием позволяет привлечь интерес учащихся к изучению новой темы, не блокируя восприятия непонятными терминами.

Учитель записывает на доске слово «Тема», выдерживает паузу до тех пор, пока все

дети не обратят внимание на руку учителя.

Учитель: Ребята, извините, но моя рука «отказывается» писать тему урока. Как вы думаете, почему рука «отказалась» записать тему урока? (Ученики высказывают свои предположения, например, такие: напишем ее позже; должны ее угадать; должны сформулировать её самостоятельно).

Учитель: Да, ребята, я предлагаю вам попробовать самостоятельно сформулировать тему и цели сегодняшнего урока. А для этого вам необходимо стать исследователями, «открывающими» новое знание.

На доске демонстрируются математические объекты . (Слайд № 6)

Учитель: Как можно одним словом или словосочетанием назвать объекты, которые вы видите на экране?

Возможные ответы: алгебра; алгебраические объекты; уравнения и системы уравнений.

При этом учащиеся аргументируют свой ответ.

Можно было бы в качестве объектов предложить детям только системы различного вида. Но есть смысл добавить несколько различных квадратных и линейных уравнений (тогда образуется группа «Уравнения», а в ней можно будет провести классификацию), чтобы это понятие «уравнение» стало рабочим инструментом и далее использовалось бы в процессе постановки цели урока и «открытия» нового знания.

Приём 2. «Логические поисковые задания: группировка »

Учитель: Разбейте эти математические объекты на группы как можно большим количеством способов. При этом постарайтесь аргументировать свои действия.

Дети предлагают свои способы разбиения (учитель записывает номера объектов по группам) , всякий раз указывая признак, использованный при выполнении этого задания.

Предполагаемые ответы учеников:

Можно разбить на две группы: (Слайд № 7)

— 1 группа – уравнения (3,4.7,5,8,11,12), потому что уравнением называется равенство, содержащее переменную, обозначенную буквой.

— 2 группа – системы уравнений (1,2,6,9,10), потому что уравнения объединены фигурной скобкой и эти уравнения рассматривают совместно.

Кроме того, каждую группу можно разбить еще на две.

Группу «Уравнения» можно разбить на две подгруппы: линейные уравнения (4; 7; 11) и квадратные уравнения: (3; 5; 8; 12).

Группу «Системы» тоже на две: линейные системы уравнений (1; 2; 9) и системы, состоящие из линейного уравнения и квадратного (или другого уравнения): (6; 10).

— Предлагаю поработать с каждой группой: расскажите об объектах группы все, что можете.

— в группе «уравнения»:

– 2х — 1 = 4 – это линейное уравнение с одним неизвестным. Дети аргументируют ответ, формулируя алгоритм его решения.

— приведенное квадратное уравнение: x 2 + 2х – 8 = 0, которое можно решить по общей формуле корней квадратного уравнения, по формуле с четным коэффициентом при х или используя теорему, обратную теореме Виета.

— в группе «системы» две подгруппы:

1-ая – системы, которые знаем и можем решить;

2-ая — системы, которые не знаем, как решать.

Что такое решение системы? ( все пары значений переменных, которые одновременно обращают уравнения системы в верные числовые равенства).

А вот убедите всех, что вы можете решить системы первой группы!

и — это линейные системы уравнений, которые можем решить способом алгебраического «сложения», потому что в первом и во втором уравнениях этих систем коэффициентами при одинаковых переменных являются либо одинаковые, либо противоположные числа.

Учитель: В чем заключается суть способа сложения?

Дети: С помощью умножения правой и левой части уравнений системы на одно и то же число нужно уравнять коэффициенты при одной из переменных, а затем заменить одно из уравнений системы его суммой или разностью с другим уравнением. При этом исключается эта переменная и получается уравнение с одной переменной. Затем находят решения системы.

Как видите, учитель предлагает детям выполнить действия с математическими объектами с аргументацией, когда они самостоятельно обращаются к теории курса математики и в качестве аргументов сами формулируют определения, свойства объектов и ставят перед собой задачи. Так происходит активное включение учащихся в процесс познания. А это и есть цель учителя.

По уже сложившейся традиции на уроке учитель обычно сам задает детям задания и наводящие вопросы. Например, такие: «Из каких видов уравнений составлены системы? Каким способом можно решить систему? Какие системы называются равносильными?» ( система, имеющая те же самые решения, что и исходная, является равносильной данной) И контролирует ответы учащихся, добиваясь верного ответа. В таком случае цель – верный ответ…

3.2. Фронтальная работа (Слайд № 8)

Учащиеся решают самостоятельно на месте. Два ученика работают за крыльями доски. Учащиеся объясняют, каким способом они решают систему. (Работают сигнальные карточки.)

4. Постановка темы урока и цели урока.

Учитель: Что общего в каждом способе решения этих систем? Что их объединяет?

— эти системы можно решить способом «алгебраического» сложения.

Возможно, что вторую систему дети смогут решить двумя (или даже тремя) путями:

— способом алгебраического « сложения»;

— подставив вместо 2х в первое уравнение 10 (новый способ);

— найти из второго уравнения х, а затем подставить его значение 5 в первое уравнение (новый способ).

Возможно, дети не назовут идею (исключение одной из переменных), объединяющую все эти способы, тогда это следует сформулировать как учебную задачу и постараться найти ответ на неё до конца урока.

— Обобщите результаты своей деятельности с математическими объектами и предположите, как будет звучать тема сегодняшнего урока?

Ответы возможны разные. Из версий учащихся выбираем более правдоподобные и записываем на доске в качестве «рабочей» формулировки темы.

1. Системы квадратных и линейных уравнений.

2. Системы нелинейных и линейных уравнений.

3. Решение системы уравнений разными способами.

Маловероятно, что версия формулировки темы «Решение системы уравнений способом подстановки» появится у детей на этом этапе . Позже на этапе «открытия» ее можно будет уточнить.

4. Этап «открытия» нового знания.

4. 1. Работа в парах.

Предлагаю поработать в парах с системами, которые не похожи на те, которые вы знаете, как решать.

Посмотрите внимательно на эти две системы уравнений. Подумайте, обсудите в парах, а затем перед всем классом расскажите о них все, что сможете.

Если дети будут затрудняться, то учитель может задать конкретный вопрос:

— Чем системы похожи и чем они отличаются?

-похожи тем, что имеют две переменные; в каждой системе есть линейное уравнение;

-отличаются тем, что в первой системе второе уравнение квадратное, а во второй нет;

-первую можно решить способом «сложения», а другую – нет.

Учитель: Предлагаю поработать сначала с первой системой, а затем – со второй.

Первая система:

Учитель: Предложите, пожалуйста, способ решения этой системы.

1) попробовать решить так, как мы знаем, то есть способом сложения.

2) поискать новый способ.

— Ребята, какой путь вы изберете: первый или второй? Ведь у нас урок «открытия»!

Учитель: Подумайте, поработав в парах, над новым способом решения.

Учащиеся высказывают предложения:

— выделить «у» из первого уравнения (у = 5х + 3) и подставить во второе уравнение системы и решить как квадратное уравнение.

здесь предложена все та же идея — идея исключения одной переменной или неизвестной.

Заметьте, что дети в процессе размышления предлагают идеи, мысли, а учитель в это время записывает на доске то, что говорят дети, чтобы перед глазами детей был образец письменной речи.

Учитель предложения учеников сам записывает на доске:

2х 2 — 15х + 7 = 0.

Учитель : Ребята, вы получили квадратное уравнение, которое умеете решать, и поэтому остановимся на этом этапе.

Учитель: Какой прием вы использовали?

Дети: Прием подстановки.

— «Открытие» состоялось! Вы «открыли» способ подстановки! Я вас всех с этим поздравляю!

— Составьте и запишите план решения системы.

Учитель: Ребята, я предлагаю вам открыть учебник на стр.150 и посмотреть на систему уравнений примера 2:

Учитель: Посмотрите на этапы решения этой системы в учебнике. Какой вывод можно сделать?

— В нашем плане пять пунктов, в учебнике их три.

— На первом этапе авторы учебника объединили два преобразования: выразить переменную из одного уравнения и подставить полученное выражение во второе уравнение, на последнем — нашли значение второй переменной и записали ответ.

Учитель: Сделайте вывод: по смыслу эти планы одинаковы?

Учитель: Сделайте ещё вывод: для чего вы составили план решения системы уравнений?

Дети: Чтобы применять его для решения системы уравнений способом подстановки.

Учитель : Попробуйте решить вторую систему новым способом по составленному плану.

Вторая система: ( Слайд №12, повт. слайда № 9)

Учитель: Подумайте и скажите, из какого уравнения проще выразить переменную?

— из первого уравнения выразить х и подставить во второе уравнение.

— из первого уравнения выразить у и подставить во второе уравнение.

Учитель: Хорошо, первый вариант выделит х, а второй – у, и подставят полученные выражения во второе уравнение. Два ученика работают на крыльях доски.

Примечание для учителей:

— здесь предложена все та же идея — идея исключения одной переменной или неизвестной.

Учитель : Проверим, какое уравнение получилось?

I вариант: х = -5 — у, II вариант: у = — 5 – х,

( — 5 – у )у = 4, х( — 5 – х ) = 4,

— 5у – у 2 = 4, — 5х – х 2 = 4,

у 2 + 5у + 4 = 0. х 2 + 5х + 4 = 0.

(Работают сигнальные карточки.)

— Зависит ли решение системы уравнений от того, какую переменную вы выразили?

-не зависит, мы получили два одинаковых по смыслу уравнения.

— Ребята, дайте название действиям, которые вы выполняли, работая с этими системами.

(выполняли преобразования, в результате которых была получена равносильная система)

— выражали переменную из одного уравнения системы и подставляли полученное выражение в другое.

А какой прием или идею вы использовали?

— идею исключения переменной или неизвестной.

-Ребята, вы почувствовали себя исследователями? Как можно назвать ваши действия?

— «Открытие» новых знаний.

— Ребята, так что же объединяет два способа решения систем уравнений: алгебраического сложения и нового?

Возможный ответ: оба способа направлены на достижение одной цели — исключить одну из переменных и получить уравнение с одним неизвестным.

— Итак, какие «старую» идею и новый способ вы использовали для решения систем уравнений?

Дети: Идею исключения переменной и способ подстановки.

— Системы, с которыми мы сегодня работали, не являются линейными, а метод, который вы «открыли» самостоятельно, в математике получил название – способ подстановки.

— Так как же более точно звучит тема сегодняшнего урока?

— «Решение системы уравнений способом подстановки».

— Верно! А теперь запишем тему урока: «Решение системы уравнений способом подстановки». Вы все хорошо справились с «открытием» новых знаний. Поздравляю!

Ребята, все что вы «открыли» сегодня, будете использовать для следующего «открытия» на уроке завтра.

Данный урок является уроком «открытия» нового знания (главное — это самостоятельное «открытие» нового знания). Применением же этих знаний учащиеся будут заниматься на следующем уроке, чтобы еще более осознать смысл «открытого» ими знания.

Если «открытие» школьниками новых знаний пройдет быстро и останется время (что маловероятно: материал сложный), то можно будет провести этап применения новых знаний (см. ниже). Поэтому этап 5 – это вариативный этап урока, который состоится только при наличии свободного времени. Подчеркиваем, что нецелесообразно обязательно стараться успеть провести этот этап, заставляя детей спешить в момент «открытия» и планировать, таким образом, информационную перегрузку детей, которая мешает интеллектуальной осмысленной деятельности школьников с содержанием математики.

5. Первичный опыт использования новых знаний (вариативный этап)

А сейчас попробуйте применить «открытие» к решению задач, которые вам предлагают авторы учебника.

5.1. Работа с учебником и печатной тетрадью. ( Два ученика работают у доски на крыльях или переносных досках, остальные – в тетрадях ).

В учебнике № 378(1а)

1(а)

Учащиеся, подумав, рассуждают примерно так: выразим из первого уравнения у = 2х+1 и подставим во второе уравнение это выражение, получим: х(2х+1) = 15, раскроем скобки и решим квадратное уравнение 2х 2 + х – 15 = 0 по общей формуле. Найдем

D = в 2 — 4ас = 121, х ₁ = 2,5; х ₂ = — 3.

Проверяем (работают сигнальные карточки).

За крылом доски ученик решает № 218 (из печатной тетради, а остальные в печатной тетради самостоятельно). Обсуждаем решение: обозначим буквой х одно число, а буквой у — второе число. Составим разность чисел: х — у = 7, получим первое уравнение. Составим произведение этих чисел: ху. Зная, что произведение этих чисел больше их утроенной суммы на 21, составим второе уравнение системы: ху-3(х+у) = 21.

Составим систему уравнений: Решим систему уравнений и найдем эти числа.

Ответ: 0 и -7 или 13 и 6.

Проверяем (работают сигнальные карточки).

Итак, какой новый способ вы использовали для решения системы уравнений?

Ответ: Способ подстановки.

Сделаем вывод: какие способы решения систем уравнений вы теперь знаете?

— Способ сложения и способ подстановки .

Что же их объединяет? – Идея исключения переменной.

6. Этап «Решение задачи на смекалку с авторского сайта Муравиных» http://muravin2007.narod.ru/p0078.htm

7. Домашнее задание (1 мин.) (Слайд №15)

8. Подведение итога урока. Рефлексия (10 мин.)

8.1 Достижение предметных и метапредметных результатов.

Вопросы к учащимся:

Что нового вы узнали сегодня на уроке?

Предполагаемые ответы : о существовании способа подстановки; о решении системы уравнений способом подстановки.

Чему научились на уроке?

(В помощь детям учитель открывает слайды 16-18 с предметными и метапредметными результатами. Опираясь на них, дети отвечают на вопросы).

3) Опыт использования каких «старых» знаний и умений вам сегодня пригодился?

Предполагаемые ответы: знание способа сложения для решения системы уравнений; свойств уравнений; умение решать квадратные и линейные уравнения; выполнение действий над числами.

4) Что вызвало у вас затруднение и почему?

5) Что вызвало у вас удивление на уроке? (Например, что можно решить системы уравнений новым способом.)

6) Какой вид деятельности понравился вам больше всего и почему?

Достижение личностных результатов

— Ребята, в начале урока вы поставили личностную цель. (Слайд №19,

Покажите зеленую карточку, если вы ее достигли, и красную, если нет. Кто хочет поделиться своими выводами вслух? (Если желающих не будет, то это нормально.)

Учитель: Ребята, сегодня первый урок изучения новой темы, поэтому в журнал я выставлю только отличные и хорошие отметки. На следующем уроке мы продолжим работу. На этом наш урок окончен.

Мы не прощаемся с вами. Сегодня вы будете общаться по скайпу с авторами наших учебников: Муравиными Георгием Константиновичем и Ольгой Викторовной, и сможете задать им свои вопросы.

Источник