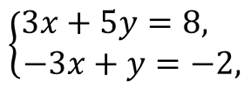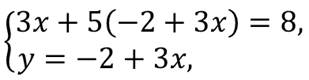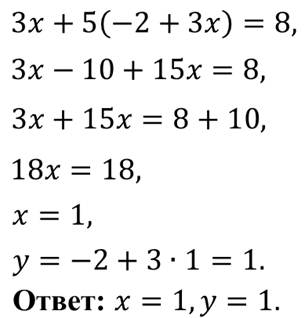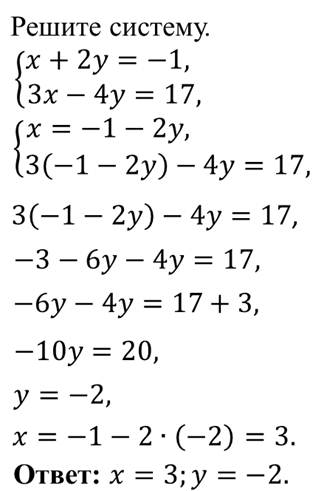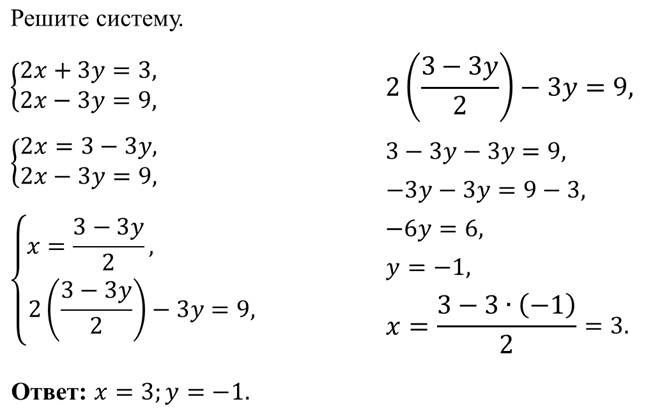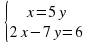Решение систем линейных уравнений способом подстановки конспект

Конспект урока 7 класс » «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ»
методическая разработка по алгебре (7 класс) на тему

Представлен конспект урока изучения нового материала по теме «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ».

Скачать:

Вложение	Размер
7_klass_moy_otkr_urok_plan-konspekt11_2016g.doc	362.5 КБ

Предварительный просмотр:

УРОК «РЕШЕНИЕ СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ С ДВУМЯ НЕИЗВЕСТНЫМИ МЕТОДОМ ПОДСТАНОВКИ»

Три пути ведут к знанию: путь размышления – это путь самый благородный, путь подражания – это путь самый легкий и путь опыта- это путь самый горький.

«Деятельность – единственный путь к знанию»

Цели урока: создать условия для формирования умения учащихся использовать способ подстановки для решения систем уравнений, воспитывать умение контролировать внимание на всех этапах урока.

Ожидаемые учебные результаты:

• подвести их к составлению алгоритма решения системы двух линейных уравнений методом подстановки;
• сформировать умение учащихся решать системы уравнений методом подстановки;
• продолжить формирование умений упрощать выражения, решать линейные уравнения с одной переменной.

Личностные: умение вести диалог на основе равноправных отношений и взаимного уважения и принятия; умение конструктивно разрешать конфликты;

• целеполагание, включая постановку новых целей, преобразование практической задачи в познавательную;
• умение самостоятельно контролировать своё время и управлять им;
• адекватно самостоятельно оценивать правильность выполнения действия и вносить необходимые коррективы в исполнение, как в конце действия, так и по ходу его реализации;
• умение прогнозировать развитие процесса.

Коммуникативные универсальные учебные действия

• формулировать и аргументировать собственное мнение и позицию
• устанавливать и сравнивать разные точки зрения, прежде чем принимать решения и делать выбор;
• аргументировать свою точку зрения, спорить и отстаивать свою позицию не враждебным для оппонентов образом;
• адекватно использовать речевые средства для решения различных коммуникативных задач; владеть устной и письменной речью;
• организовывать и планировать учебное сотрудничество с учителем и сверстниками, определять цели и функции участников, способы взаимодействия; планировать общие способы работы;
• осуществлять контроль, коррекцию, оценку действий партнёра, уметь убеждать;

Познавательные универсальные учебные действия

• создавать и преобразовывать модели и схемы для решения задач;
• осуществлять выбор наиболее эффективных способов решения задач в зависимости от конкретных условий;
• устанавливать причинно-следственные связи;
• строить логическое рассуждение, включающее установление причинно-следственных связей

Длительность урока: 1 академический час (45 мин)

Место проведения урока: кабинет математики

Оснащение урока : презентация и информационно-технологические материалы; учебник математики, ПК.

Тип и вид урока: Урок изучения нового материала.

① Мотивация учебной деятельности . Постановка учащимися целей и задач урока .

Прочитайте слова , которые выбраны девизом урока.

Как вы их понимаете.

Почему именно их я выбрала в качестве девиза? Нам предстоит разобраться

Каким путём пойти и какой для каждого более удобен

Источник

Решение систем линейных уравнений способом подстановки

Урок 42. Алгебра 7 класс

В данный момент вы не можете посмотреть или раздать видеоурок ученикам

Чтобы получить доступ к этому и другим видеоурокам комплекта, вам нужно добавить его в личный кабинет, приобрев в каталоге.

Получите невероятные возможности

Конспект урока «Решение систем линейных уравнений способом подстановки»

· показать еще один способ решения систем линейных уравнений – способ подстановки.

На прошлом уроке мы с вами говорили о системе линейных уравнений с двумя переменными.

Нам уже знаком графический способ решения систем линейных уравнений.

Мы также отмечали, что графический способ чаще всего позволяет находить решения лишь приближённо.

Сегодня на уроке мы познакомимся с ещё одним способом решения систем линейных уравнений с двумя переменными, который называют способом подстановки.

Итак, рассмотрим следующую систему

Заметим, что во втором уравнении системы коэффициент при у равен 1, поэтому мы легко можем выразить переменную у через переменную х.

Далее мы подставим вместо у в первое уравнение системы это выражение и получим уравнение с одной переменной х.

Решим это уравнение.

Вот так мы с вами решили систему уравнений способом подстановки.

Таким образом, чтобы решить систему уравнений способом подстановки, надо:

1. выразить из какого-нибудь уравнения системы одну переменную через другую;

2. подставить вместо этой переменной полученное выражение в другое уравнение системы;

3. решить получившееся уравнение с одной переменной;

4. найти соответствующее значение второй переменной.

Ранее мы с вами говорили о равносильных уравнениях, то есть уравнениях, которые имеют одни и те же корни.

То же самое можно сказать и о системах уравнений.

Системы уравнений с двумя переменными, имеющие одни и те же решения, называются равносильными.

Системы, которые не имеют решений, также являются равносильными.

Ну а теперь давайте решим несколько систем рассмотренным выше способом.

На этом уроке мы рассмотрели алгоритм решения систем линейных уравнений способом подстановки и научились решать системы этим способом.

Источник

План – конспект урока по алгебре в 7-м классе на тему: «Решение систем линейных уравнений методом подстановки»

План – конспект урока по алгебре в 7-м классе на тему:

« Решение систем линейных уравнений методом подстановки »

Образовательные: – разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки.

Воспитательные: – воспитание познавательной активности, чувства ответственности, культуры общения, культуры диалога.

Развивающие: — развитие зрительной памяти, математически грамотной речи, логического мышления, сознательного восприятия учебного материала.

1. Предметные: разобрать, в чем состоит метод подстановки решения систем линейных уравнений; вывести алгоритм применения этого метода; сформировать умение решать системы уравнений методом подстановки продолжить формирование мотивации обучающихся к изучению предмета.

2. Метапредметные: развивать операционный стиль мышления, способствовать приобретению учащимися навыков общения при совместной работе, активизировать их творческое мышление; продолжить формирование определенных компетенций обучающихся, которые будут способствовать их эффективной социализации, навыков самообразования и самовоспитания

3. Личностные: воспитывать культуру, способствовать формированию личностных качеств, направленных на доброжелательное, толерантное отношение к людям, жизни; воспитывать инициативу и самостоятельность в деятельности; подвести к пониманию необходимости изучаемой темы для успешной подготовки к государственной итоговой аттестации.

Тип урока: урок изучения новой темы.

Вид урока: комбинированный.

Оборудование: мультимедийный проектор, компьютер.

Запись даты и темы урока.

Напомнить учащимся, что на предыдущих уроках мы учились решать системы линейных уравнений.

Что такое система двух линейных уравнений с двумя переменными? (Математическая модель, состоящая из двух линейных уравнений с двумя переменными)

Что мы называем решением системы уравнений? (Пара чисел (х;у), которая одновременно является решением первого и второго уравнений системы)

Какими способами мы умеем решать системы уравнений? (Метод подбора и графический метод)

Проверка домашнего задания (работа в парах)

Для повторения предлагаю вам выполнить следующие задания:

1. Раскрыть скобки (устно с повторением правил раскрытия скобок)

2. Выразить из уравнения одну переменную через другую. (задание выполняется на доске с комментариями)

Вопрос: Какую переменную легче выразить через другую в каждом из уравнений и почему?

3. Является ли пара чисел (2;3) решением системы уравнений:

4. Сколько решений имеет система уравнений:

Изучение нового материала.

Системы уравнений с двумя переменными, которые имеют одни и те же решения или не имеют решений, называются равносильными.

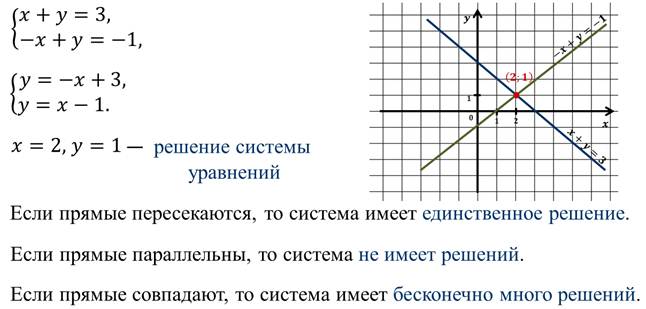
Эти системы равносильны, т. к. имеют одно и то же решение (2;1). (проверить устно, подставив в каждую из систем)

Эти системы равносильны, т. к. каждая из них не имеет решений. (проверить устно)

При решении системы уравнений с помощью преобразований ее заменяют более простой равносильной системой. Одним из способов решения системы является способ методом подстановки. Давайте решим систему уравнений, составляя таблицу.

Решим методом подстановки

1. Выражаем. Из любого уравнения выражаем одну переменную.

Видно, что во втором уравнении имеется переменная x с коэффициентом 1, отсюда получается, что легче всего выразить переменную x из второго уравнения.

2. Подставляем. Подставляем в другое уравнение вместо выраженной переменной, полученное значение.

2. После того как выразили х через у, подставляем в первое уравнение «3+10 y » вместо переменной « x ».

3. Решаем полученное уравнение с одной переменной.

4. Находим вторую переменную.

3. Решаем полученное уравнение.

2(3+10 y ) +5 y =1 ( раскрываем скобки)

Подставить найденное значение у в выражение х через у.

Точки принято записывать на первом месте пишем переменную x, а на втором переменную y.

Ответ: (1; -0,2) или х=1 и у=-0,2

Необходимо обратить внимание учащихся, что выражать следует ту переменную, при которой стоит более « удобный » коэффициент (в частности + — 1).

Мы составили алгоритм решения системы методом подстановки.

Формирование умений и навыков.

Желательно, чтобы в течение урока учащиеся запомнили алгоритм решения систем уравнений методом подстановки и могли его применять, не обращаясь к записям в тетрадях и разобранным примерам.

Задание на уроке: № 12.5( аб), № 12.2( а), № 12.8( аб)

Для решения каждой системы следует вызывать к доске по одному учащемуся. Необходимо требовать, чтобы они вслух комментировали все свои шаги.

– Какие вы знаете способы решения систем уравнений?

– Сформулируйте алгоритм решения систем уравнений способом подстановки

– Из какого уравнения системы лучше выражать переменную?

Источник

Конспект урока «Решение систем уравнений способом подстановки»

Разработка урока по системе «перевёрнутый урок»

Просмотр содержимого документа
«Конспект урока «Решение систем уравнений способом подстановки»»

Решение систем линейных уравнений способом подстановки

Лось Татьяна Николаевна

ГУО «Гимназия г. Иваново»

Изучение нового материала в рамках системы «Перевернутый урок»

Дидактическая цель урока

Предполагается, что к концу урока учащиеся:

будут знать способ подстановки.

будут уметь пользоваться способом подстановки при решении систем линейных уравнений;

смогут выполнить задания выходного контроля.

Задачи личностного развития

Создание условий для развития способности к саморегуляции, самоорганизации посредством использования методики “Перевернутый урок” (формирование учебно-познавательной компетенции и компетенции самоопределения)

Создание условий для развития приемов мыслительной деятельности (анализа, синтеза, аналогии) через использование эвристических приемов обучения.

Подготовительная работа учителя

Слово учителя в конце предыдущего урока:

Вы можете использовать и другие источники, которые найдёте сами. Так как тема новая, у вас могут возникнуть вопросы, ответы на которые мы найдём на следующем уроке.

После разбора задания вам предстоит выполнить несколько заданий и составить алгоритм решения систем линейных уравнений способом подстановки. Кроме этого постарайтесь определить, что было самым сложным в восприятии материала. Надеюсь, эта тема вызовет у вас истинный интерес.

Используемые педагогические технологии, методы, приемы

Образовательная стратегия «Перевернутый урок»

Дидактическое обеспечение урока

Раздаточный материал: задания для самостоятельного выполнения

Список учебной и дополнительной литературы;

Учебное пособие по алгебре для 9 класса (Л.Б.Шнепермана)

Как вам кажется, есть ли польза от стойки на голове? Если да, то в чем?

(улучшается кровоснабжение головы и обогащение питательными веществами и кислородом – улучшается цвет лица, состояние волос; обращение потока крови дает сердцу возможность отдохнуть; улучшается пищеварение; укрепляются мышцы спины и плеч)

Легко ли выполнить эту стойку? Конечно, нет!

Вот и мы сегодня работаем с новым материалом, используя непростой подход в обучении – «превернутый урок».

Формулировка темы урока, принятие дидактической цели урока

С новым материалом вы познакомились дома. А, значит, сами можете назвать тему урока: «Решение систем линейных уравнений способом подстановки»

Число, классная работа

Как вам кажется, какие цели мы поставим перед этим уроком? (Систематизируем информацию, полученную дома самостоятельно, научимся ее применять)

Активизация мыслительной деятельности

1. Из предложенных уравнений выберите те, которые являются линейными уравнениями с двумя переменными:

а) 3х + 3у – 1 = 0 г) 1/х +1/у = 3

б) 3х 2 + у = 5 д) х + у = 3

в) 5х + 5 = 6х е) 1/2х + у – 5/6 = 0

Что такое система линейных уравнений с двумя переменными?

Что значит решить систему линейных уравнений?

Что называется решением системы линейных уравнений?

Выразите х из уравнения: 5х-10у=20; 12х + 3у= 1,2

Выразите у из уравнения: у+5х=0; 4х- 3у=5

Назовите алгоритм, который вы составили.

Проверка понимания изученного

№ 3.21 (1, 3) на доске с комментарием

Работа в парах по вариантах

Решите систему уравнений методом подстановки:

а)

б)

в)

Решите систему уравнений методом подстановки:

а)

б)

в)

5. Психологическая пауза

Проверим реакцию. Предлагается притча: однажды индийский раджа устроил для своих подданных соревнование: кто пробежит по стене, неся на голове кувшин с водой, не разлив ни капли. Под стеной стояла масса народу, каждый из которых кричал, дудел в трубы, бил в барабаны. Лишь одному человеку удалось донести кувшин, не разлив воду. Когда раджа спросил, как ему это удалось, он ответил, что ничего не слышал, т.к. нес воду. Учитель называет слова (каникулы, экзамен, решение, рождество, система, Астана, подстановка, метель, Минск, уравнение, праздник, Москва. стол, Киев, Париж), учащиеся должны расслышать: 1) математические термины, 2) столицы государств.

6.Проверка усвоения материала

Займите свои места за компьютером. Выполните тест.

7.Рефлексия и подведение итогов

Какую цель мы ставили на урок? Достигли ли её? Продолжите фразу

На уроке я научился….

Мне было трудно…

Самым интересным было…

Самым трудным было…

Дома вам предстоит решить из учебника № 3.22 (неч.)

Источник