Решение систем линейных неравенств с двумя переменными графическим способом

Решение систем линейных неравенств графически

Система ограничений такой задачи состоит из неравенств от двух переменных:
и целевая функция имеет вид F = C ₁ x + C₂y, которую необходимо максимизировать.

Ответим на вопрос: какие пары чисел ( x; y ) являются решениями системы неравенств, т. е. удовлетворяют каждому из неравенств одновременно? Другими словами, что значит решить систему графически?
Предварительно необходимо понять, что является решением одного линейного неравенства с двумя неизвестными.
Решить линейное неравенство с двумя неизвестными – это значит определить все пары значений неизвестных, при которых неравенство выполняется.
Например, неравенству 3x – 5 y ≥ 42 удовлетворяют пары (x , y) : (100, 2); (3, –10) и т. д. Задача состоит в нахождении всех таких пар.
Рассмотрим два неравенства: ax + by≤ c, ax + by≥ c. Прямая ax + by = c делит плоскость на две полуплоскости так, что координаты точек одной из них удовлетворяют неравенству ax + by >c , а другой неравенству ax + +by

Пусть для определенности a&lt 0, b>0, c >0. Все точки с абсциссой x₀, лежащие выше P (например, точка М), имеют y_M>y₀, а все точки, лежащие ниже точки P, с абсциссой x₀, имеют y_N c, образующие полуплоскость, а с другой стороны – точки, для которых ax + by

Знак неравенства в полуплоскости зависит от чисел a, b , c.
Отсюда вытекает следующий способ графического решения систем линейных неравенств от двух переменных. Для решения системы необходимо:

1. Для каждого неравенства выписать уравнение, соответствующее данному неравенству.
2. Построить прямые, являющиеся графиками функций, задаваемых уравнениями.
3. Для каждой прямой определить полуплоскость, которая задается неравенством. Для этого взять произвольную точку, не лежащую на прямой, подставить ее координаты в неравенство. если неравенство верное, то полуплоскость, содержащая выбранную точку, и является решением исходного неравенства. Если неравенство неверное, то полуплоскость по другую сторону прямой является множеством решений данного неравенства.
4. Чтобы решить систему неравенств, необходимо найти область пересечения всех полуплоскостей, являющихся решением каждого неравенства системы.

Эта область может оказаться пустой, тогда система неравенств не имеет решений, несовместна. В противном случае говорят, что система совместна.
Решений может быть конечное число и бесконечное множество. Область может представлять собой замкнутый многоугольник или же быть неограниченной.

Рассмотрим три соответствующих примера.

Пример 1. Решить графически систему:
x + y – 1 ≤ 0;
–2 x – 2y + 5 ≤ 0.

Решение:

• рассмотрим уравнения x+y–1=0 и –2x–2y+5=0 , соответствующие неравенствам;
• построим прямые, задающиеся этими уравнениями.

Рисунок 2

Определим полуплоскости, задаваемые неравенствами. Возьмем произвольную точку, пусть (0; 0). Рассмотрим x+ y– 1 0, подставим точку (0; 0): 0 + 0 – 1 ≤ 0. значит, в той полуплоскости, где лежит точка (0; 0), x + y – 1 ≤ 0, т.е. полуплоскость, лежащая ниже прямой, является решением первого неравенства. Подставив эту точку (0; 0), во второе, получим: –2 ∙ 0 – 2 ∙ 0 + 5 ≤ 0, т.е. в полуплоскости, где лежит точка (0; 0), –2x – 2y + 5≥ 0, а нас спрашивали, где –2x – 2y + 5 ≤ 0, следовательно, в другой полуплоскости – в той, что выше прямой.
Найдем пересечение этих двух полуплоскостей. Прямые параллельны, поэтому плоскости нигде не пересекаются, значит система данных неравенств решений не имеет, несовместна.

Пример 2. Найти графически решения системы неравенств:

Рисунок 3
1. Выпишем уравнения, соответствующие неравенствам, и построим прямые.
x + 2y– 2 = 0

x	2	0
y	0	1

y – x – 1 = 0

x	0	2
y	1	3

y + 2 = 0;
y = –2.
2. Выбрав точку (0; 0), определим знаки неравенств в полуплоскостях:
0 + 2 ∙ 0 – 2 ≤ 0, т.е. x + 2y– 2 ≤ 0 в полуплоскости ниже прямой;
0 – 0 – 1 ≤ 0, т.е. y –x– 1 ≤ 0 в полуплоскости ниже прямой;
0 + 2 =2 ≥ 0, т.е. y + 2 ≥ 0 в полуплоскости выше прямой.
3. Пересечением этих трех полуплоскостей будет являться область, являющаяся треугольником. Нетрудно найти вершины области, как точки пересечения соответствующих прямых

Рассмотрим еще один пример, в котором получившаяся область решения системы не ограничена.

Пример 3 . Решить графически систему
Выпишем уравнения, соответствующие неравенствам, и построим прямые.
Рисунок 4
x + y – 1 = 0

x	0	1
y	1	0

y – x – 1 = 0

x	0	–1
y	1	0

Определим знаки в полуплоскостях. Выберем точку (0; 0):
0 – 0 – 1 ≤ 0, т.е. y – x – 1 ≤ 0 ниже прямой;
0 + 0 – 1 ≤ 0, т.е. x + y – 1 ≤ 0 ниже прямой.
Пересечением двух полуплоскостей является угол с вершиной в точке А(0;1). Эта неограниченная область является решением исходной системы неравенств.

• Решение онлайн
• Видеоинструкция

Источник

Линейные неравенства с двумя переменными и их системы

Линейное неравенство с двумя переменными и его решение

Неравенство вида ax+by $ \begin \lt \\ \gt \\ \le \\ \ge \end $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.

Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac<1> <2>x-8y \gt 7$

Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.

Например: для неравенства $2x+5y \lt 6$

пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина

пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь

Графическое представление линейного неравенства с двумя переменными

Графическим представлением линейного неравенства с двумя переменными вида ax+by$ \begin \lt \\ \gt \\ \le \\ \ge \end $ c является полуплоскость с границей ax+by = c .

Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.

Графическое решение системы линейных неравенств с двумя переменными

Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.

Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.

Пересечение обозначают знаком $\cap$.

Найдём графическое решение системы линейных неравенств:

Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).

Примеры

Пример 1. Найдите графическое представление линейного неравенства:

Представление – полуплоскость под границей, сама граница не входит

Представление – полуплоскость под границей, сама граница входит

Представление – полуплоскость справа от границы, сама граница входит

Представление – полуплоскость под границей, сама граница не входит

Пример 2*. Найдите графическое решение системы линейных неравенств:

Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)

Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.

Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.

Подберите состав грузовиков для выполнения заказа.

Пусть x — количество грузовиков по 3т, y – по 5т.

По условию задачи:

$$ <\left\< \begin 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end \right.> $$

Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.

Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна

Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит

Ответ: 2 грузовика по 3т и 5 грузовиков по 5т

Источник

Графическое решение систем неравенств с двумя переменными

В презентации на конкретных примерах представлен способ решения систем неравенств с двумя переменными на координатной плоскости. Материал предназначен для объяснения темы «Системы неравенств с двумя переменными».в 9 классе (Алгебра, 9 класс, автор Макарычев Ю.Н.)

Просмотр содержимого документа
«Графическое решение систем неравенств с двумя переменными»

с двумя переменными

К учебнику Ю.Н.Макарычева

Алгебра, 9 класс, Глава III §

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Решение системы неравенств

с двумя переменными

Решением системы неравенств с двумя переменными называется пара значений этих переменных, являющаяся как решением первого неравенства, так и второго неравенства системы.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

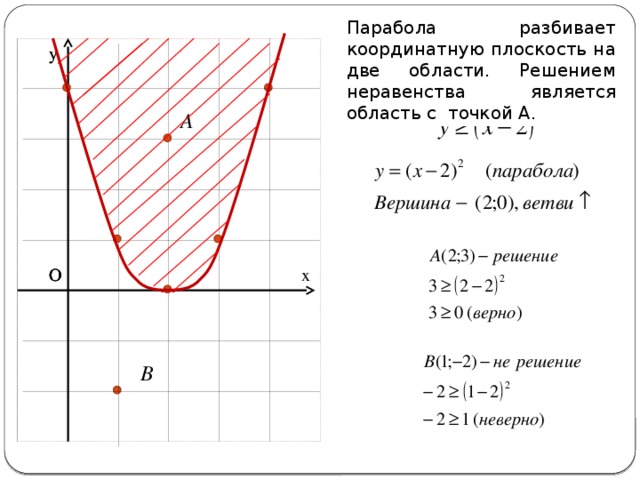
Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

Изображение множества решений системы неравенств с двумя переменными на координатной плоскости

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

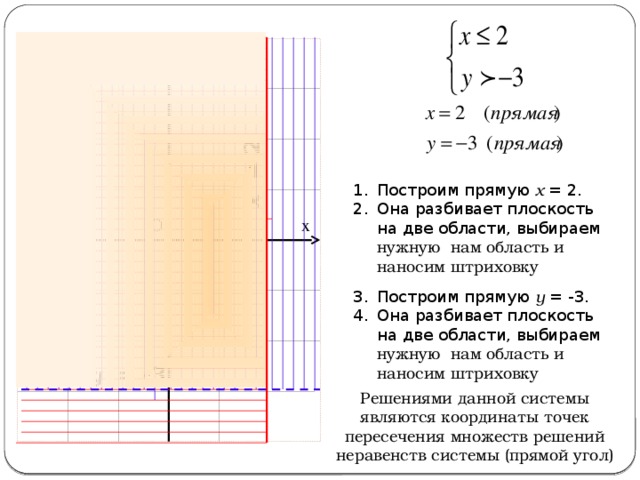
• Построим прямую х = 2.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = -3.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (прямой угол)

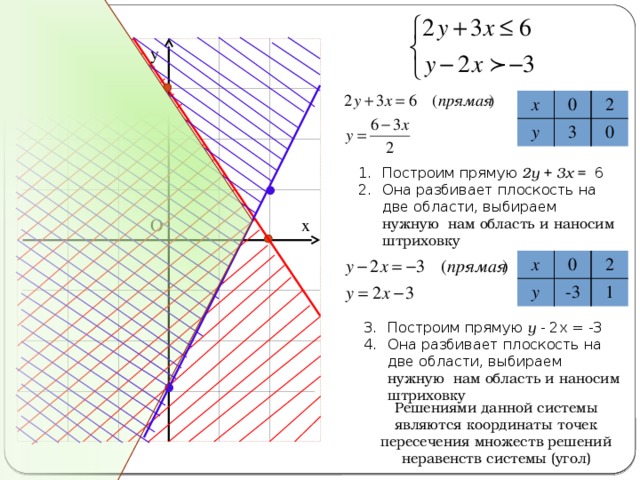
• Построим прямую 2у + 3х = 6
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у — 2х = -3
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (угол)

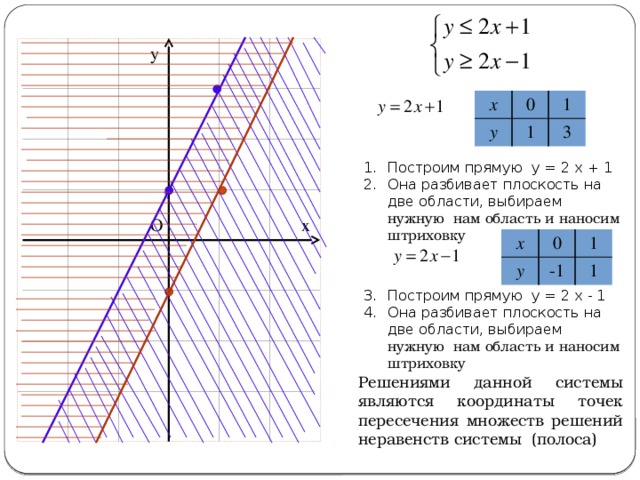
• Построим прямую у = 2 х + 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = 2 х — 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (полоса)

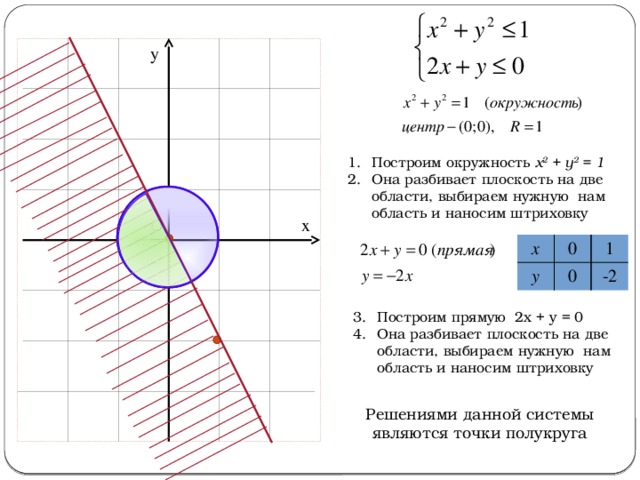
• Построим окружность х2+ у2= 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую 2х + у = 0
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки полукруга

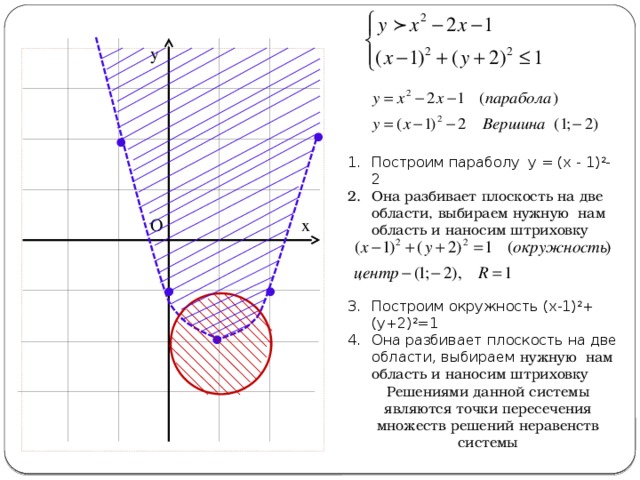
• Построим параболу у = (х — 1) 2 -2
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим окружность (х-1) 2 +(у+2) 2 =1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки пересечения множеств решений неравенств системы

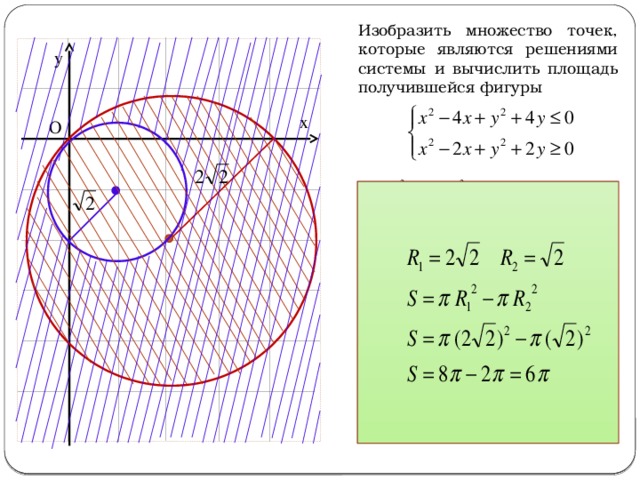
Изобразить множество точек, которые являются решениями системы и вычислить площадь получившейся фигуры

Источник