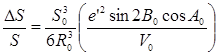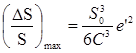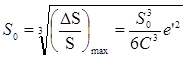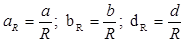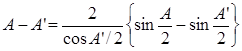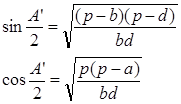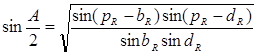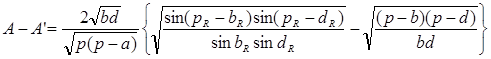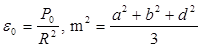Решение сферического треугольника по теореме лежандра и способу аддитаментов
РЕШЕНИЕ СФЕРИЧЕСКОГО ТРЕУГОЛЬНИКА ПО ТЕОРЕМЕ
ЛЕЖАНДРА И СПОСОБУ АДДИТАМЕНТОВ
Треугольник триангуляции 1-го класса
Определить координаты точки С.
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ:
При помощи программы Prima решаем обратную геодезическую задачу и определяем длину стороны с:
Таблица 1
Решение обратной геодезической задачи
2. Теорема Лежандра утверждает: если стороны плоского и сферического треугольника соответственно равны, то углы плоского треугольника равны углам сферического, уменьшенным на одну треть сферического избытка.
Если обозначить А, В, С углы сферического треугольника, полученные из измерений, а 







то А / , В / , С / есть углы плоского треугольника, стороны которого равны соответственно сторонам сферического треугольника.
Вычисление сферического избытка выполняется в таблице 2.
Таблица 2
Вычисление сферического избытка
3. Решение треугольника триангуляции по теореме Лежандра выполняется в таблице 3.
Стороны плоского треугольника вычисляем по теореме синусов, используя уравненные углы плоского треугольника и известную сторону.
4.Решим сферический треугольник по способу аддитаментов, принимая следующее утверждение:
если углы плоского треугольника равны соответствующим углам сферического, то стороны плоского треугольника меньше соответствующих сторон сферического на величину аддитамента.
Для сторон треугольников меньше 100 км аддитаменты вычисляются по формулам:
K =1/6 R 2 (значение длин сторон берется в км, аддитаменты получаем в м).
Вычисления производим в таблице 4.
По известной стороне сферического треугольника находим аддитамент и сторону плоского треугольника: S плоского= S сферического-А.
Применяя теорему синусов, по известной стороне плоского треугольника и по углам находим значения недостающих сторон плоского треугольника. Вычисляем аддитаменты найденных сторон и определяем стороны сферического треугольника по формулам: S сферического=Sплоского+А.
5. Вычисляем азимуты направлений АС и ВС, используя уравненные углы сферического треугольника и азимут направления АВ.
6. Используя программу Prima решаем прямую геодезическую задачу и вычисляем широту и долготу точки С от двух исходных точек (А и В).
Решение треугольника триангуляции по теореме Лежандра
Источник
2.2. Решение треугольников по способу аддитаментов.
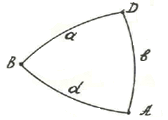
Сохраняя прежние обозначения для сферического треугольника ABC имеем:
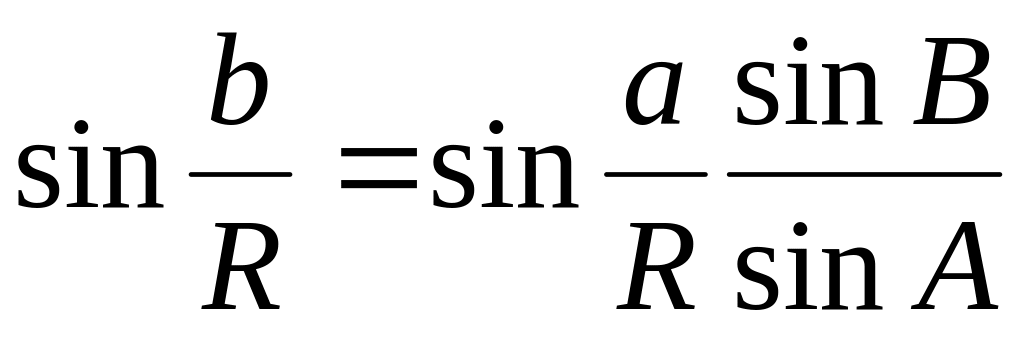
Раскладывая 
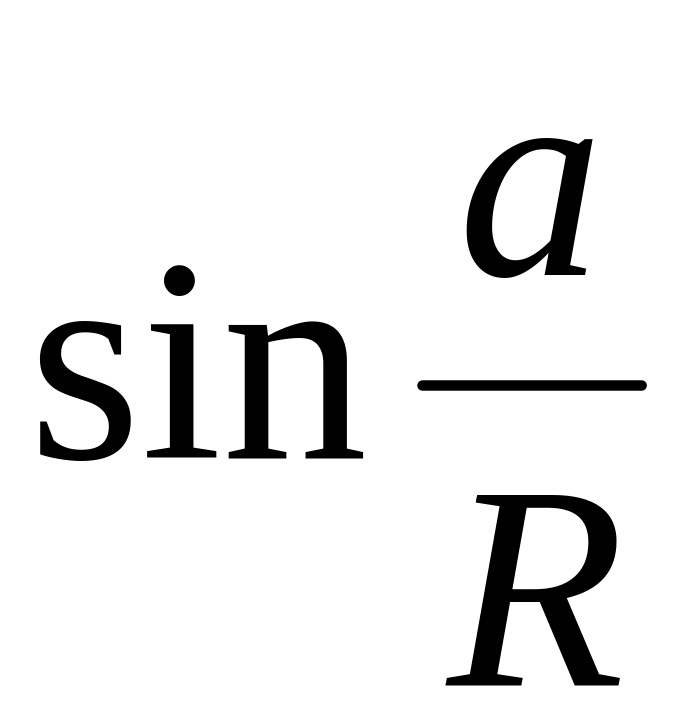
или в логарифмическом виде:
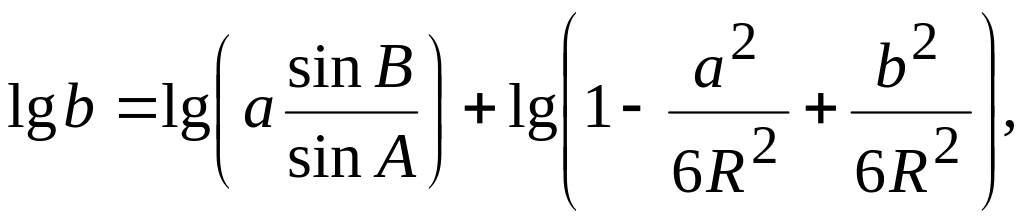
lg(1 + x) = μ x — 
где μ – переходный модуль от натуральных к десятичным логарифмам.

Величины 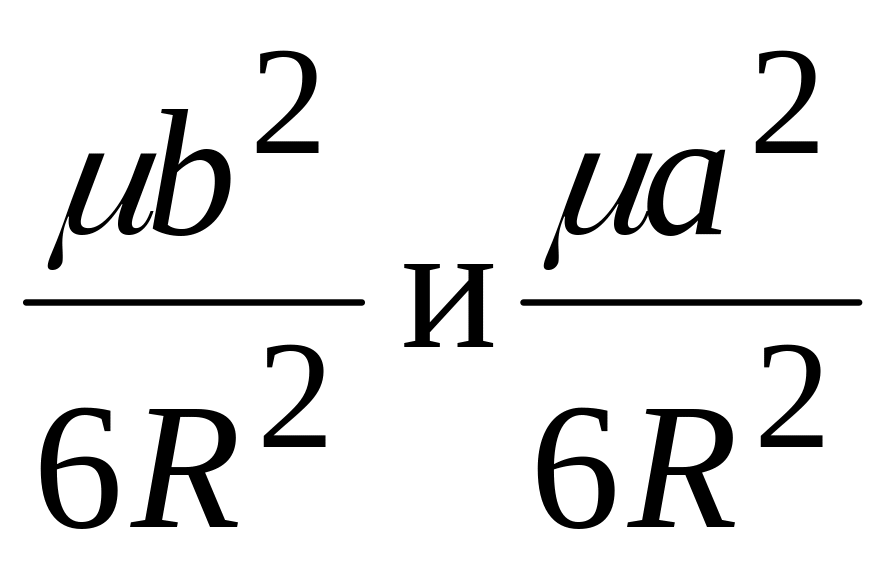
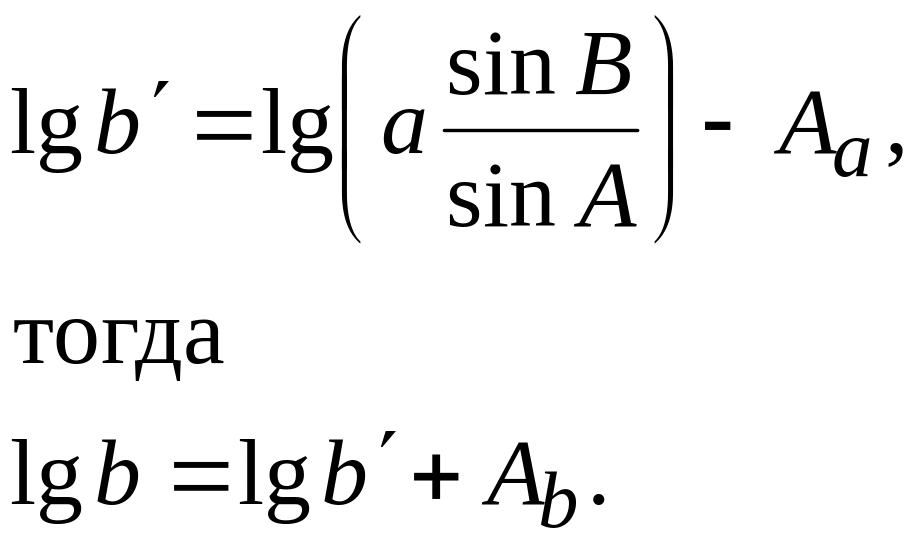
Пусть имеем цепь треугольников рис. 2.3, тогда

Если в логарифм исходной стороны a ввести поправку — Aa, т.е. вычислить lg a΄=lg a — Aa и с этим новым значением a΄ исходной стороны вычислить стороны треугольников, рассматривая их сферические углы как углы плоских треугольников, то получим:

Отсюда вытекает следующий порядок вычислений сторон сферических треугольников по способу аддитаментов:
1) из логарифма исходной стороны вычитается ее аддитамент и таким образом вычисляется 1ga‘,
2) с исправленным значением логарифма исходной стороны решаются треугольники как плоские без изменений сферических углов, т. е. определяются lg b‘, lg c‘, lg d‘;
3) вычисленные значения lg b‘, lg c‘, lg d‘ исправляют соответственными аддитаментами по формулам (2.9) и получают искомые значения сторон треугольников триангуляции.
Радиус шара, необходимый для вычисления аддитаментов, теоретически должен иметь свое, значение для каждого треугольника, а именно: он должен быть равен среднему радиусу кривизны для средней широты треугольника. Однако практически при вычислении треугольников по способу аддитаментов достаточно получить радиус для некоторой средней точки триангуляции, расстояние которой от крайних треугольников не должно превышать некоторого предела, зависящего от точности вычислений. Найдем это расстояние.
Определим изменение аддитамента в зависимости от изменения R:
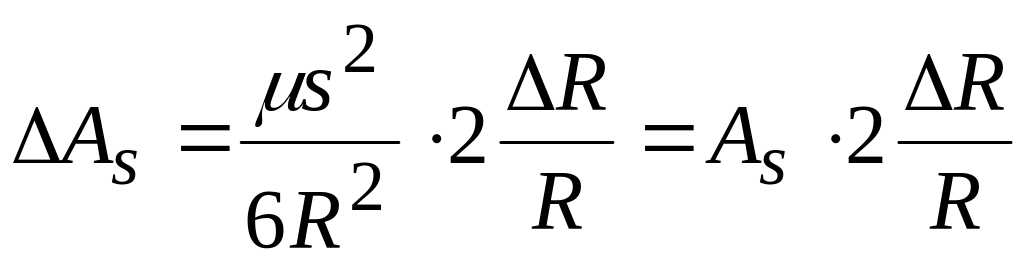
Поставив условие, чтобы ошибка в аддитаменте, обусловленная неточностью принятой широты, не превышала 0,5 единицы 8 знака логарифма (т.е. 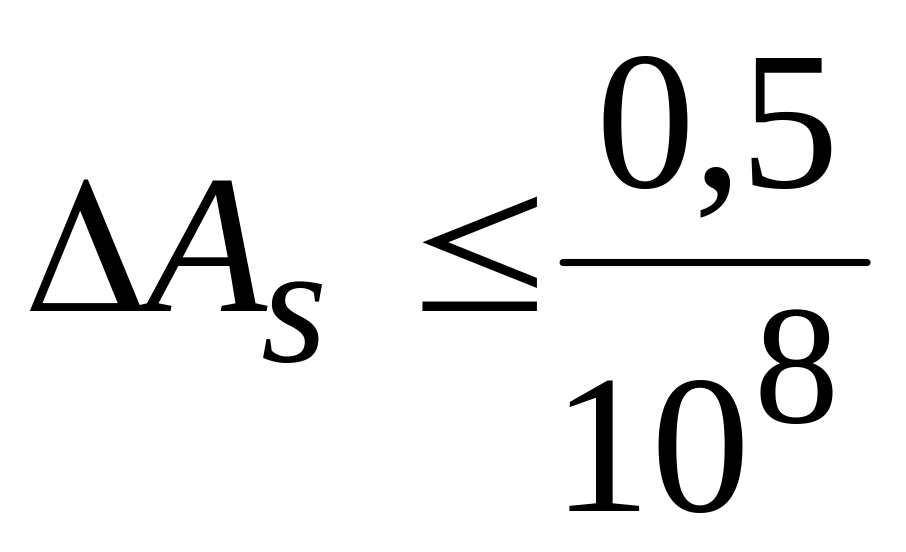
Следовательно, составив таблицу аддитаментов для какой-либо широты, средней для данной триангуляции, мы можем пользоваться этой таблицей для решения треугольников, отстоящих на 5° по широте к северу и югу от точки с данной широтой. Другими словами, в пределах пояса, ограниченного параллелями, шириной в 1000 км, мы можем не считаться с изменением R1, если только аддитаменты вычислены для средней широты взятого пояса.

В семизначных логарифмических таблицах на каждой странице внизу приводятся величины:
где Аx — аддитамент аргумента х, выраженного в секундах, следовательно,

Таким образом, если стороны треугольников выразить в угловой мере, то аддитаменты можно вычислять, пользуясь указанными логарифмическими таблицами.
Рассмотрим пример решения треугольника по способу аддитаментов.
Источник
Лабораторная работа: Решение сфероидических треугольников
| Название: Решение сфероидических треугольников Раздел: Рефераты по математике Тип: лабораторная работа Добавлен 17:37:25 08 июня 2011 Похожие работы Просмотров: 788 Комментариев: 19 Оценило: 2 человек Средний балл: 5 Оценка: неизвестно Скачать |
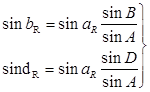 |
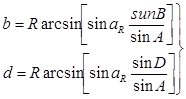
Если в треугольнике известны все стороны, то на основании теоремы косинуса стороны, будем иметь:
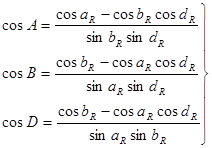

Совершенно очевидно, приведенные алгоритмы — это не единственный путь решения сферических треугольников. Возможно использование и других формул сферической тригонометрии при решении тех же треугольников и с теми же самыми исходными данными.
На практике решение треугольников непосредственно по формулам сферической тригонометрии удобно и оправдано в том случае, если это решение выполняется на ЭВМ. Если же оно ведется в ручную — не по программе на ЭВМ, а с использованием настольных средств вычислительной техники, то решение, непосредственно, по формулам сферической тригонометрии становится практически громоздким. Действительно, в этом случае приходится с большой степенью точности вычислять ряд вспомогательных величин (R, a/R, sin (a/R), sin (b/R)), которые в конечном итоге не нужны.
Для решения малых сферических треугольников с использованием настольной вычислительной техники разработаны два способа: способ аддитаментов и способ решения сферических треугольников c применением теоремы Лежандра.
Суть способа заключается в замене решения сферического треугольника решением плоского с углами, равными углам сферического треугольника, и измененной (на аддитамент) исходной стороной с последующим введением в полученные из решения плоского треугольника стороны поправок (аддитаментов).
Рассмотрим теоретические основы этого способа.
Полагая, что стороны сферического треугольника — малые величины (S 1/2 углы сферического и плоского треугольников будут отличаться на небольшие величины. Исходя из этого примем с ошибкой на величины второго порядка малости (если за первый порядок принять А — А’):
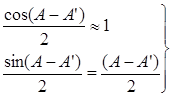
И тогда из (19) с учетом (20), находим
Заменяя синусы и косинусы углов известными соотношениями:
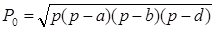
После разложения квадратов разностей и дальнейших простых преобразований, окончательно получаем:
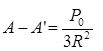
Можно по аналогии написать формулы для разностей (В — В’) и (D— D’):
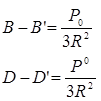
Суммируя левые и правые части выражений (21) и (22), находим для треугольника:
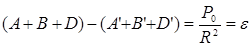
С учетом равенства (23), формулы (21) и (22) можно представить в следующем виде:
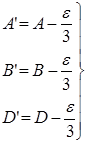
которые и выражают теорему Лежандра.
Если при разложении синусов в ряд удерживались бы члены пятого порядка малости, то в результате были бы получены более точные формулы:
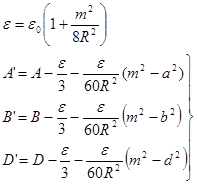
Где
Источник



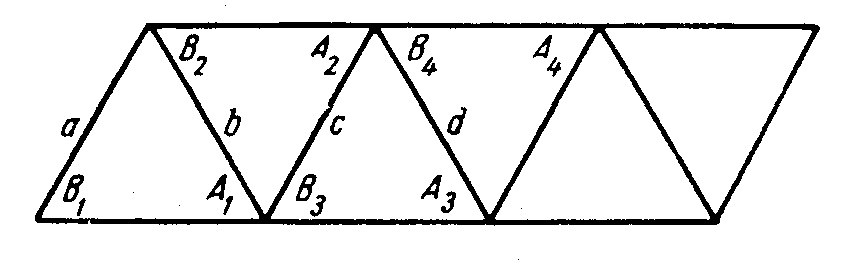
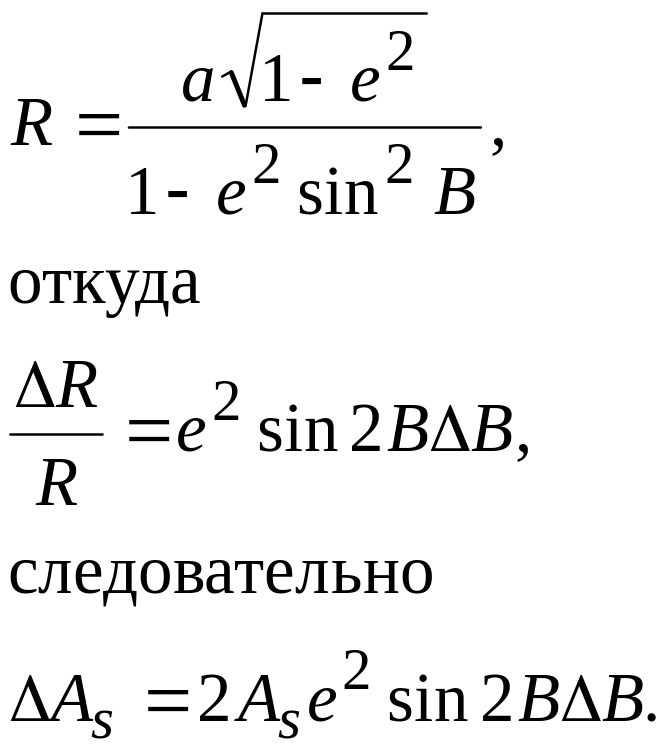

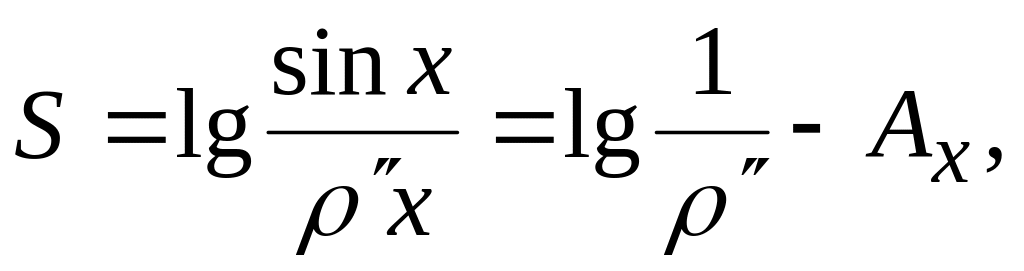
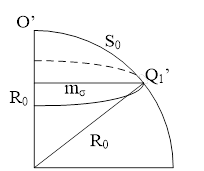
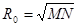 в некоторой точке О (рис. 1),
в некоторой точке О (рис. 1),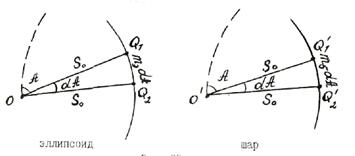
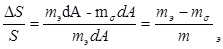 (1)
(1)
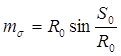 (2)
(2)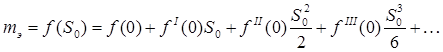
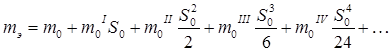 (3)
(3)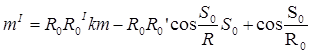
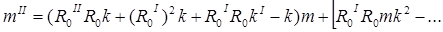
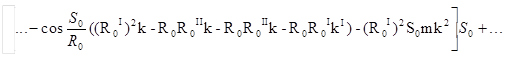
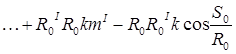
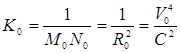 (4)
(4)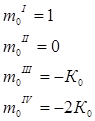
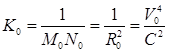 (5)
(5)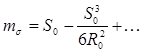 (6)
(6)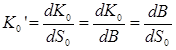
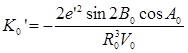
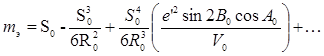 (7)
(7)