Решение примеров удобным способом правило

При этом саму запись (9 — 4) тоже можно назвать разностью.

1. Свойство нуля при вычитании
   Если из числа вычесть нуль, получится само число.
   a — 0 = a
   Если из числа вычесть само число, то получится нуль.
   a — a = 0
2. Свойство вычитания суммы из числа
   Чтобы вычесть сумму из числа, можно вычесть из этого числа одно слагаемое, из полученной разности — второе слагаемое.
   a — (b + c) = a — b — c
3. Свойство вычитания числа из суммы
   Чтобы вычесть число из суммы, можно вычесть его из одного слагаемого, а к результату прибавить оставшееся слагаемое.
   (a + b) — c = (a — c) + b (если a > c или а = с)
   (a + b) — c = (b — c) + a (если b > c или b = с)

Примеры использования свойств сложения и вычитания

Мы узнали основные свойства сложения и вычитания — осталось попрактиковаться. Чтобы ничего не забыть, используйте эту шпаргалку:

Пример 1

Вычислить сумму слагаемых с использованием разных свойств:

а) 4 + 3 + 8 = (4 + 3) + 8 = 7 + 8 = 15

б) 9 + 11 + 2 = (9 + 2) + 11 = 11 + 11 = 22

в) 30 + 0 + 13 = 30 + 13 = 43

Пример 2

Применить разные свойства при вычислении разности:

а) 25 — 0 — 2 = 25 — 2 = 23

б) 18 — (1 + 4) = 18 — 1 — 4 = 17 — 4 = 13

Пример 3

Найти значение выражения удобным способом:

а) 11 + 10 + 3 + 9 = (11 + 10) + (3 + 9) = 21 + 11 = 32

б) 16 — (4 + 3) + 7 = 16 — 4 — 3 + 7 = (16 — 4) — 3 + 7 = 12 — 3 + 7 = 9 + 7 = 16

Источник

Порядок выполнения действий, правила, примеры

Когда мы работаем с различными выражениями, включающими в себя цифры, буквы и переменные, нам приходится выполнять большое количество арифметических действий. Когда мы делаем преобразование или вычисляем значение, очень важно соблюдать правильную очередность этих действий. Иначе говоря, арифметические действия имеют свой особый порядок выполнения.

В этой статье мы расскажем, какие действия надо делать в первую очередь, а какие после. Для начала разберем несколько простых выражений, в которых есть только переменные или числовые значения, а также знаки деления, умножения, вычитания и сложения. Потом возьмем примеры со скобками и рассмотрим, в каком порядке следует вычислять их. В третьей части мы приведем нужный порядок преобразований и вычислений в тех примерах, которые включают в себя знаки корней, степеней и других функций.

Порядок вычисления простых выражений

В случае выражений без скобок порядок действий определяется однозначно:

1. Все действия выполняются слева направо.
2. В первую очередь мы выполняем деление и умножение, во вторую – вычитание и сложение.

Смысл этих правил легко уяснить. Традиционный порядок записи слева направо определяет основную последовательность вычислений, а необходимость сначала умножить или разделить объясняется самой сутью этих операций.

Возьмем для наглядности несколько задач. Мы использовали только самые простые числовые выражения, чтобы все вычисления можно было провести в уме. Так можно быстрее запомнить нужный порядок и быстро проверить результаты.

Условие: вычислите, сколько будет 7 − 3 + 6 .

Решение

В нашем выражении скобок нет, умножение и деление также отсутствуют, поэтому выполняем все действия в указанном порядке. Сначала вычитаем три из семи, затем прибавляем к остатку шесть и в итоге получаем десять. Вот запись всего решения:

7 − 3 + 6 = 4 + 6 = 10

Ответ: 7 − 3 + 6 = 10 .

Условие: в каком порядке нужно выполнять вычисления в выражении 6 : 2 · 8 : 3 ?

Решение

Чтобы дать ответ на этот вопрос, перечитаем правило для выражений без скобок, сформулированное нами до этого. У нас здесь есть только умножение и деление, значит, мы сохраняем записанный порядок вычислений и считаем последовательно слева направо.

Ответ: сначала выполняем деление шести на два, результат умножаем на восемь и получившееся в итоге число делим на три.

Условие: подсчитайте, сколько будет 17 − 5 · 6 : 3 − 2 + 4 : 2 .

Решение

Сначала определим верный порядок действий, поскольку у нас здесь есть все основные виды арифметических операций – сложение, вычитание, умножение, деление. Первым делом нам надо разделить и умножить. Эти действия не имеют приоритета друг перед другом, поэтому выполняем их в написанном порядке справа налево. То есть 5 надо умножить на 6 и получить 30 , потом 30 разделить на 3 и получить 10 . После этого делим 4 на 2 , это 2 . Подставим найденные значения в исходное выражение:

17 − 5 · 6 : 3 − 2 + 4 : 2 = 17 − 10 − 2 + 2

Здесь уже нет ни деления, ни умножения, поэтому делаем оставшиеся вычисления по порядку и получаем ответ:

17 − 10 − 2 + 2 = 7 − 2 + 2 = 5 + 2 = 7

Ответ: 17 − 5 · 6 : 3 − 2 + 4 : 2 = 7 .

Пока порядок выполнения действий не заучен твердо, можно ставить над знаками арифметических действий цифры, означающие порядок вычисления. Например, для задачи выше мы могли бы записать так:

.

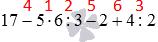
Если у нас есть буквенные выражения, то с ними мы поступаем точно так же: сначала умножаем и делим, затем складываем и вычитаем.

Что такое действия первой и второй ступени

Иногда в справочниках все арифметические действия делят на действия первой и второй ступени. Сформулируем нужное определение.

К действиям первой ступени относятся вычитание и сложение, второй – умножение и деление.

Зная эти названия, мы можем записать данное ранее правило относительно порядка действий так:

В выражении, в котором нет скобок, сначала надо выполнить действия второй ступени в направлении слева направо, затем действия первой ступени (в том же направлении).

Порядок вычислений в выражениях со скобками

Скобки сами по себе являются знаком, который сообщает нам нужный порядок выполнения действий. В таком случае нужное правило можно записать так:

Если в выражении есть скобки, то первым делом выполняется действие в них, после чего мы умножаем и делим, а затем складываем и вычитаем по направлению слева направо.

Что касается самого выражения в скобках, его можно рассматривать в качестве составной части основного выражения. При подсчете значения выражения в скобках мы сохраняем все тот же известный нам порядок действий. Проиллюстрируем нашу мысль примером.

Условие: вычислите, сколько будет 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 .

Решение

В данном выражении есть скобки, поэтому начнем с них. Первым делом вычислим, сколько будет 7 − 2 · 3 . Здесь нам надо умножить 2 на 3 и вычесть результат из 7 :

7 − 2 · 3 = 7 − 6 = 1

Считаем результат во вторых скобках. Там у нас всего одно действие: 6 − 4 = 2 .

Теперь нам нужно подставить получившиеся значения в первоначальное выражение:

5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 5 + 1 · 2 : 2

Начнем с умножения и деления, потом выполним вычитание и получим:

5 + 1 · 2 : 2 = 5 + 2 : 2 = 5 + 1 = 6

На этом вычисления можно закончить.

Ответ: 5 + ( 7 − 2 · 3 ) · ( 6 − 4 ) : 2 = 6 .

Не пугайтесь, если в условии у нас содержится выражение, в котором одни скобки заключают в себе другие. Нам надо только применять правило выше последовательно по отношению ко всем выражениям в скобках. Возьмем такую задачу.

Условие: вычислите, сколько будет 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) .

Решение

У нас есть скобки в скобках. Начинаем с 3 + 1 + 4 · ( 2 + 3 ) , а именно с 2 + 3 . Это будет 5 . Значение надо будет подставить в выражение и подсчитать, что 3 + 1 + 4 · 5 . Мы помним, что сначала надо умножить, а потом сложить: 3 + 1 + 4 · 5 = 3 + 1 + 20 = 24 . Подставив найденные значения в исходное выражение, вычислим ответ: 4 + 24 = 28 .

Ответ: 4 + ( 3 + 1 + 4 · ( 2 + 3 ) ) = 28 .

Иначе говоря, при вычислении значения выражения, включающего скобки в скобках, мы начинаем с внутренних скобок и продвигаемся к внешним.

Допустим, нам надо найти, сколько будет ( 4 + ( 4 + ( 4 − 6 : 2 ) ) − 1 ) − 1 . Начинаем с выражения во внутренних скобках. Поскольку 4 − 6 : 2 = 4 − 3 = 1 , исходное выражение можно записать как ( 4 + ( 4 + 1 ) − 1 ) − 1 . Снова обращаемся к внутренним скобкам: 4 + 1 = 5 . Мы пришли к выражению ( 4 + 5 − 1 ) − 1 . Считаем 4 + 5 − 1 = 8 и в итоге получаем разность 8 — 1 , результатом которой будет 7 .

Порядок вычисления в выражениях со степенями, корнями, логарифмами и иными функциями

Если у нас в условии стоит выражение со степенью, корнем, логарифмом или тригонометрической функцией (синусом, косинусом, тангенсом и котангенсом) или иными функциями, то первым делом мы вычисляем значение функции. После этого мы действуем по правилам, указанным в предыдущих пунктах. Иначе говоря, функции по степени важности приравниваются к выражению, заключенному в скобки.

Разберем пример такого вычисления.

Условие: найдите, сколько будет ( 3 + 1 ) · 2 + 6 2 : 3 − 7 .

Решение

У нас есть выражение со степенью, значение которого надо найти в первую очередь. Считаем: 6 2 = 36 . Теперь подставим результат в выражение, после чего оно примет вид ( 3 + 1 ) · 2 + 36 : 3 − 7 .

Дальше действуем по знакомому алгоритму: считаем, сколько у нас получится в скобках, потом в оставшемся выражении выполняем умножение и деление, а следом – сложение и вычитание.

( 3 + 1 ) · 2 + 36 : 3 − 7 = 4 · 2 + 36 : 3 − 7 = 8 + 12 − 7 = 13

Ответ: ( 3 + 1 ) · 2 + 6 2 : 3 − 7 = 13 .

В отдельной статье, посвященной вычислению значений выражений, мы приводим и другие, более сложные примеры подсчетов в случае выражений с корнями, степенью и др. Рекомендуем вам с ней ознакомиться.

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 57. Разные способы вычислений.

Перечень вопросов, рассматриваемых в теме:

Как выполнять устно вычисления в случаях, сводимых к действиям в пределах 1000, используя различные приёмы устных вычислений?

Как выбирать удобный способ?

Как выполнять проверку вычислений?

Глоссарий по теме:

Круглым называется число, которое делится на 10, 100, 1000 и так далее, без остатка.

Каждая цифра в записи многозначного числа занимает определённое место – позицию. Место (позицию) в записи числа, на котором стоит цифра, называют разрядом.

Единицы, десятки, сотни, тысячи и т. д. иначе ещё называют разрядными единицами:
единицы называют единицами 1-го разряда
десятки называют единицами 2-го разряда
сотни называют единицами 3-го разряда и т. д.

Сложение – арифметическое действие в математике, в результате которого два или более чисел объединяется в единое целое, оно обозначается знаком «+». Слагаемое, слагаемое, сумма – главные составляющие математического действия сложения.

Вычитание – арифметическое действие, обратное сложению и обозначается оно знаком «-». Уменьшаемое, вычитаемое, разность- главные составляющие математического действия вычитания.

Основная и дополнительная литература по теме урока:

Моро М.И. Учебник для 3 класса четырехлетней начальной школы. М. «Просвещение» — 2017. С. 68-69

Волкова С.И. математика. Проверочные работы. 3 кл. — М.: Просвещение, 2018.С. 72-73

Рудницкая В.Н. Математика. Дидактические материалы. Ч.1. 3 кл. – М. «Вентана- Граф», 2016, с. 9-12

Теоретический материал для самостоятельного изучения

Вам уже знакомы приёмы устных вычислений в пределах 1000.

Но наша цель не просто узнать о них, а уверенно ими пользоваться.

Часто ученики допускают ошибки при решении примеров.

Сегодня мы более подробно остановимся на таких случаях и разберемся, как их избежать

Надеюсь, что после урока вы даже сможете посоревноваться с друзьями в устном счёте.

Вспомним приёмы устных вычислений, с которыми познакомились на прошлом уроке.

работаем с разрядными слагаемыми

работаем с общим количеством десятков.

Чтобы быстро и правильно решать такие примеры надо уметь выбирать более удобный способ.

А как выбрать удобный способ?

Выберем из этих примеров те, которые удобнее решать, работая с разрядными слагаемыми.

Согласитесь, что эти примеры будет легко решить, представив одно из слагаемых в виде суммы разрядных слагаемых.

Например: 420 + 50, десятки сложим с десятками и прибавим сотни, а при решении примера 320 + 500 сложим сотни и прибавим десятки.

Что же не так с остальными примерами?

Внимательно посмотри на числа. При выполнении действий с десятками происходит переход через разряд. Это вызывает затруднения.

Именно поэтому здесь удобнее воспользоваться вторым способом – работать с общим количеством десятков.

Рассмотрим первый пример: 150 — 90

Пользуясь первым способом, нам пришлось бы из 50 вычитать 90, а это невозможно.

Приходит на помощь второй способ:

15 дес. — 9 дес. это 6 дес. или 60. Никаких проблем.

Тоже самое с остальными примерами.

Но есть ещё одна опасность при решении подобных примеров на вычитание.

Рассмотрим два примера:

560 — 300 и 600 — 240.

Обрати внимание, в первом примере десятки в уменьшаемом, а во втором — в вычитаемом.

На это очень важно обращать внимание!

Понаблюдаем за решением.

560 — 300 = (500 — 300) + 60 = 260

600 — 240 = (600 — 200) — 40 = 360

В первом случае десятки прибавляем, а во втором вычитаем. Так как в первом случае вычитаем только сотни – 300, а во втором – сотни и десятки — 240

Если же ты сомневаешься в результате или просто хочешь убедиться в правильности, можно выполнить проверку.

Проверка выполняется обратным действием. Сложение проверяем вычитанием и наоборот.

Проверка: 260 + 300 = 560

Проверка: 360 + 240 = 600

Сегодня мы раскрыли вам секреты приёмов устного сложения и вычитания.

Пользуйтесь ими и удачи!

Задания тренировочного модуля:

1. Распределите карточки с примерами на две группы по более удобному способу решения.

1. Поставьте в ячейке напротив «+», если согласны с решением, и «-», если не согласны.

1. Ученик решил примеры. Выберите отметку, которую он получил за работу.

Источник