- Определитель матрицы онлайн
- Предупреждение
- Примеры вычисления определителя матрицы
- Методы вычисления определителей
- Вычисления определителей второго порядка
- Методы вычисления определителей третьего порядка
- Правило треугольника
- Правило Саррюса
- Разложение определителя по строке или столбцу
- Разложение определителя по элементам строки или столбца
- Приведение определителя к треугольному виду
- Теорема Лапласа
- Определители четвертого порядка
Определитель матрицы онлайн
Данный онлайн калькулятор вычисляет определитель матрицы. Дается подробное решение. Для вычисления определителя матрицы выбирайте порядок (размер) квадратной матрицы. Введите данные в ячейки. Выберите метод решения и нажмите на кнопку «Вычислить». Теоретическую часть смотрите на странице определитель матрицы.
Предупреждение
Инструкция ввода данных. Числа вводятся в виде целых чисел (примеры: 487, 5, -7623 и т.д.), десятичных чисел (напр. 67., 102.54 и т.д.) или дробей. Дробь нужно набирать в виде a/b, где a и b целые или десятичные числа. Примеры 45/5, 6.6/76.4, -7/6.7 и т.д.
Примеры вычисления определителя матрицы
Пример 1. Найти определитель матрицы
 . |
Для вычисления определителя матрицы, приведем матрицу к верхнему треугольному виду.
Выбираем самый большой по модулю ведущий элемент столбца 1. Для этого меняем местами строки 1 и 2. При этом меняется знак определителя на «−»:
 . |
Исключим элементы 1-го столбца матрицы ниже главной диагонали. Для этого сложим строки 2,3 со строкой 1, умноженной на -1/78,-2/78 соответственно:
 . |
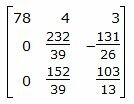Исключим элементы 2-го столбца матрицы ниже главной диагонали. Для этого сложим строку 3 со строкой 2, умноженной на -5928/9048:
 . |
Мы привели матрицу к верхнему треугольному виду. Определитель матрицы равен произведению всех элементов главной диагонали (учитывая знак определителя):
 . |
Пример 2. Найти определитель матрицы A, разложением определителя по первой строке:
| . |
Для вычисления определителя матрицы методом разложения по первой строке, вычисляем произведение каждого элемента первой строки на соответствующее алгебраическое дополнение и суммируем полученные результаты:
Источник
Методы вычисления определителей
В общем случае правило вычисления определителей $n$-го порядка является довольно громоздким. Для определителей второго и третьего порядка существуют рациональные способы их вычислений.
Вычисления определителей второго порядка
Чтобы вычислить определитель матрицы 
второго порядка, надо от произведения элементов главной диагонали отнять произведение элементов побочной диагонали:
Задание. Вычислить определитель второго порядка $\left| \begin
Решение. $\left| \begin
Методы вычисления определителей третьего порядка
Для вычисления определителей третьего порядка существует такие правила.
Правило треугольника
Схематически это правило можно изобразить следующим образом:
Произведение элементов в первом определителе, которые соединены прямыми, берется со знаком «плюс»; аналогично, для второго определителя — соответствующие произведения берутся со знаком «минус», т.е.
Методы вычисления определителей не по зубам? Тебе ответит эксперт через 10 минут!
Задание. Вычислить определитель $\left| \begin
Решение. $\left| \begin
$$+3 \cdot 3 \cdot 1-(-1) \cdot 1 \cdot 1-3 \cdot(-2) \cdot 3-4 \cdot 3 \cdot(-2)=54$$
Правило Саррюса
Справа от определителя дописывают первых два столбца и произведения элементов на главной диагонали и на диагоналях, ей параллельных, берут со знаком «плюс»; а произведения элементов побочной диагонали и диагоналей, ей параллельных, со знаком «минус»:
Задание. Вычислить определитель $\left| \begin
Решение. 
$$+(-1) \cdot 4 \cdot(-2)-(-1) \cdot 1 \cdot 1-3 \cdot 3 \cdot(-2)-3 \cdot 4 \cdot(-2)=54$$
Разложение определителя по строке или столбцу
Определитель равен сумме произведений элементов строки определителя на их алгебраические дополнения. Обычно выбирают ту строку/столбец, в которой/ом есть нули. Строку или столбец, по которой/ому ведется разложение, будет обозначать стрелкой.
Задание. Разложив по первой строке, вычислить определитель $\left| \begin
Решение. $\left| \begin
Этот метод позволяет вычисление определителя свести к вычислению определителя более низкого порядка.
Задание. Вычислить определитель $\left| \begin
Решение. Выполним следующие преобразования над строками определителя: из второй строки отнимем четыре первых, а из третьей первую строку, умноженную на семь, в результате, согласно свойствам определителя, получим определитель, равный данному.
Определитель равен нулю, так как вторая и третья строки являются пропорциональными.
Для вычисления определителей четвертого порядка и выше применяется либо разложение по строке/столбцу, либо приведение к треугольному виду, либо с помощью теоремы Лапласа.
Разложение определителя по элементам строки или столбца
Задание. Вычислить определитель $\left| \begin
Решение. Предварительно выполним элементарные преобразования над строками определителя, сделав как можно больше нулей либо в строке, либо в столбце. Для этого вначале от первой строки отнимем девять третьих, от второй — пять третьих и от четвертой — три третьих строки, получаем:
Полученный определитель разложим по элементам первого столбца:
Полученный определитель третьего порядка также разложим по элементам строки и столбца, предварительно получив нули, например, в первом столбце. Для этого от первой строки отнимаем две вторые строки, а от третьей — вторую:
$$=4 \cdot(2 \cdot 8-4 \cdot 4)=0$$
Последний и предпоследний определители можно было бы и не вычислять, а сразу сделать вывод о том, что они равны нулю, так как содержат пропорциональные строки.
Приведение определителя к треугольному виду
С помощью элементарных преобразований над строками или столбцами определитель приводится к треугольному виду и тогда его значение, согласно свойствам определителя, равно произведению элементов стоящих на главной диагонали.
Задание. Вычислить определитель $\Delta=\left| \begin
Решение. Сначала делаем нули в первом столбце под главной диагональю. Все преобразования будет выполнять проще, если элемент $a_<11>$ будет равен 1. Для этого мы поменяем местами первый и второй столбцы определителя, что, согласно свойствам определителя, приведет к тому, что он сменит знак на противоположный:
Далее получим нули в первом столбце, кроме элемента $a_<11>$ , для этого из третьей строки вычтем две первых, а к четвертой строке прибавим первую, будем иметь:
Далее получаем нули во втором столбце на месте элементов, стоящих под главной диагональю. И снова, если диагональный элемент будет равен $\pm 1$ , то вычисления будут более простыми. Для этого меняем местами вторую и третью строки (и при этом меняется на противоположный знак определителя):
Далее делаем нули во втором столбце под главной диагональю, для этого поступаем следующим образом: к третьей строке прибавляем три вторых, а к четвертой — две вторых строки, получаем:
Далее из третьей строки выносим (-10) за определитель и делаем нули в третьем столбце под главной диагональю, а для этого к последней строке прибавляем третью:
Ответ. $\Delta=-80$
Теорема Лапласа
Пусть $\Delta$ — определитель $n$-го порядка. Выберем в нем произвольные $k$ строк (или столбцов), причем $k \leq n-1$ . Тогда сумма произведений всех миноров $k$-го порядка, которые содержатся в выбранных $k$ строках (столбцах), на их алгебраические дополнения равна определителю.
Задание. Используя теорему Лапласа, вычислить определитель $\left| \begin
Решение. Выберем в данном определителе пятого порядка две строки — вторую и третью, тогда получаем (слагаемые, которые равны нулю, опускаем):
Источник
Определители четвертого порядка
Методы их вычисления
Определение. Выражение
называется определителем четвертого порядка. Этот определитель можно записать в виде:
, (6)
где 
— минор элемента, стоящего на пересечении i-ой строки и j-го столбца, 
-алгебраическое дополнение этого элемента.
Формулу (6) можно записать с помощью значка суммирования 
:
, (7)
Формула (7) называется разложением определителя по элементам
i-ой строки. Можно записать и разложение определителя по элементам j-го столбца:
(8)
Метод понижения порядка определителя основан на обращении всех, кроме одного, элементов строки или столбца определителя в нуль с помощью свойств определителей.
Пример 11.Вычислить определитель
.
Решение. Прибавим элементы первой строки к элементам второй строки:
.
Элементы первой строки умножим на (-2) и прибавим к элементам третьей строки:
.
Элементы первой строки умножим на (-1) и прибавим к элементам четвертой строки:
.
Разложим полученный определитель по элементам первого столбца
Переставим первые две строки, при этом знак определителя изменится на противоположный, одновременно вынесем общий множитель 3 элементов третьего столбца за знак определителя:
.
Умножим элементы первой строки на (-2) и прибавим к элементам второй строки:
.
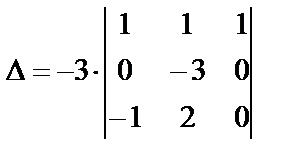
Полученный определитель разложим по элементам второй строки
Пример 12. Вычислить определитель 
.
Внимание. ошибка после 2 действия: при умножении 1 строки на (-2) и прибавлении к 4 строке получается 0 1 -3 2.
Решение. Поменяем местами первую и вторую строки, при этом по свойству 2 знак определителя изменится на противоположный:
.
Сначала элементы первой строки умножим на (-2) и прибавим к элементам второй и четвертой строк, а затем элементы первой строки умножим на (-3) и прибавим к элементам третьей строки, получим:
.
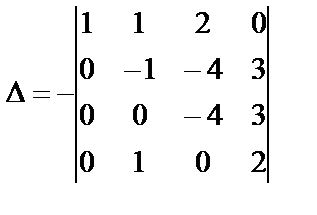
Элементы второй строки прибавим к элементам четвертой строки:
.
Элементы третьей строки умножим на (-1) и прибавим к элементам четвертой строки:
.
Получим определитель треугольного вида, значение которого равно произведению элементов главной диагонали 
.
Пример 13. Вычислить определитель
.
Решение.Разложим определитель по элементам третьей строки
Полученные определители третьего порядка вычислим по правилу треугольника
Задания для самостоятельного решения.
2. Решить уравнения:
3. Решить неравенства:
4. Вычислить определители:
Ответы: 1. а)7; б)26; в)0; г)0; д)30. 2. а)5; б)2; в)2;
г) 
3. а) 
б) 
в) 
г)[-1;7]. 4. а)-24; б)-40; в)-9; г)57; д)-5; е)1; ж)1; з)55; и)30; к)48; л)0; м)-1004; н)150.
Матрицы
Основные понятия
Определение. Матрицей называется прямоугольная таблица чисел, содержащая m строк одинаковой длины и n столбцов одинаковой длины, которая записывается в виде
(9)
или, сокращенно, 
, где 
, (т.е. 
) – номер строки, 
(т.е. 
) – номер столбца, числа 
называются элементами матрицы. Матрицу 
называют матрицей размера 
и пишут 
. Например. 
, 
.
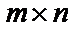
Определение. Две матрицы и 
равны между собой, если их размеры совпадают, а их соответствующие элементы равны, т.е. 
, если 
, где 
.
Например. 
Так как размеры матриц совпадают 
и соответствующие элементы равны, поэтому матрицы 
и 
равны, т.е.
Определение. Матрица, у которой число строк равно числу столбцов, называется квадратной. Квадратную матрицу размера 
называют матрицей n-го порядка.
Например. 
т.е. дана матрица второго порядка.
Определение. Квадратная матрица, у которой все элементы, кроме элементов главной диагонали, равны нулю, называются диагональной.
Матрица 
— диагональная.
Определение. Диагональная матрица, у которой каждый элемент главной диагонали равен единице, называется единичной. Обозначается буквой 
.
или 
.
Определение. Квадратная матрица называется треугольной, если все элементы, расположенные над главной диагональю (или под главной диагональю), равны нулю.
или 
— треугольные матрицы.
Важной характеристикой квадратной матрицы порядка n является ее определитель (или детерминант), который обозначается 
или 
. 
.
Определение. Квадратная матрица, у которой определитель отличен от нуля, т.е. 
, называется невырожденной. В противном случае матрица называется вырожденной.
Например, 
Матрица А – вырожденная.
Матрица В – невырожденная.
Определение. Матрица, все элементы которой равны нулю, называется нулевой и обозначается буквой О.
В матричном исчисление матрицы О и Е играют роль чисел 0 и 1 в арифметике.
Определение. Матрица, содержащая одну строку, называется матрицей-строкой
Матрица, содержащая один столбец, называется матрицей-столбцом
Матрица размера 
, состоящая из одного числа, отождествляется с этим числом, т.е. 
есть 3.
Определение. Матрица, полученная из данной заменой каждой ее строки столбцом с тем же номером, называется матрицей транспонированной к данной. Обозначается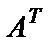 
.
Если 
, то 
, если 
, то 
.
Транспонированная матрица обладает следующим свойством: 
.
Источник
