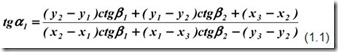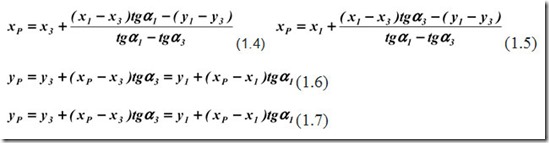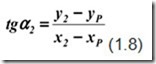Решение обратной геодезической засечки способом деламбра

Обратная угловая засечка в геодезии

Доброго времени суток, уважаемые читатели моего блога!

Определение положения точки посредством измерения углов (направлений) на определяемой точке, на три и более пункта с известными координатами в геодезии – это и есть обратная угловая засечка. Если исходных пунктов три – это однократная угловая засечка, если больше – многократная угловая засечка.

Французский математик Л.Потенот в 1692 году предложил математическое решение задачи по определению координат искомой точки по известным координатам трёх других точек. Сейчас решений этой задачи существует более ста. Один из видов решения – использование формул Жана Деламбра, французского геодезиста, астронома, метролога. Обратная засечка по Деламбру определяется через нумерацию исходных точек и углов по часовой стрелке с выбранным начальным направлением.

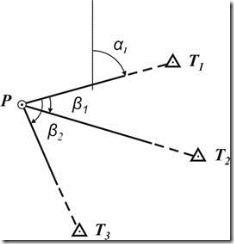
На рисунке 1 начерчена схема обратной засечки в соответствии с формулами Деламбра. Пункты триангуляции Т1, Т2, Т3 – исходные, точка (пункт) Р – определяемая, выбрано начальное направление – РТ1, на пункте Р измерены углы β1, β2 в направлении пунктов Т2, Т3.

Рис. 1. Обратная однократная угловая засечка (схема).

Сначала нужно определить дирекционный угол начального направления РТ1:

Итог: прямая угловая засечка с известными углами направлений с точки Р на исходные пункты. Известный способ определения координат Хр, Ур точки Р – это необходимое и достаточное применение формул Гаусса, которые выражаются через координаты исходных точек, вернее, их приращения:

Вычисления координат пункта Р происходит дважды; процесс вычисления, таким образом контролируется. Угол α2 высчитывается так:

Необходимо понимать, что значения α2, которое произведено по формуле 1.8, может не соответствовать значению, вычисленному по формуле 1.2 – на 180 градусов. Это связано с тем, что знаки числителя, знаменателя (формула 5.1) не могут определить приращения координат ∆х, ∆у. Контролируемое значение α2 требует определения знаков и четверти на карте проекта, где отмечены вставки точек методом обратной засечки.

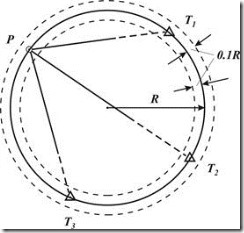
Аксиомой является то, что у обратной угловой засечки с тремя исходными пунктами нет решения, если пункт, который определяется, расположен на одной и той же окружности, что и исходные точки. Такая окружность называется «опасной». Удаление от неё определяемой точки на 0,1 х R (радиус окружности), обеспечит точность местоположения пункта, который является искомым.

Рис. 2. «Опасная» зона в обратной угловой засечке.

Если при схематичном составлении на карте (плане) обратной угловой засечки, пункт, который вычисляется, расположен в границах треугольника с вершинами – исходными пунктами (точками), можно констатировать, что «опасной окружности» здесь нет. В иных случаях, сообразно геометрическим законам, на карте (плане) строится окружность, которая проходит через 3 исходных пункта, после чего визуально определяется «опасная» зона для вычисляемого пункта.

Для работы по формулам обратной угловой засечки существует программа вычислений в режиме он-лайн, которая базируется на сайте map-info.ru. Ещё один способ определения необходимого пункта – это обратная линейно – угловая засечка. О ней поговорим в следующий раз.

На этом все друзья. Спасибо за внимание. Отличного Вам дня и хорошего настроения. Пока!!

Источник

Обратная однократная засечка. Формулы обратной однократной засечки

1. Обратная однократная засечка.

Обратной угловой засечкой называется определение положения пункта путем измерения углов или направлений на определяемом пункте не менее чем на три пункта, координаты которых известны.

В том случае, когда исходных пунктов всего лишь три, обратная угловая засечка называется однократной. В том случае, когда исходных пунктов более трех – обратная угловая засечка называется многократной.

Задача определения положения точки на плоскости по трем данным точкам обратной засечкой известна под названием задачи Потенота (Л.Потенот – французский математик; годы жизни 1660-1732 гг; в 1692 году предложил наиболее удачное аналитическое решение определения координат точки по трем известным точкам). Существует очень большое количество решений (более ста) этой задачи.

Из всех существующих способов решения рассмотрим решение по формулам Деламбра.

( Деламбр (Delambre) Жан Батист Жозеф (19.09.1749, Амьен, — 19.08.1822, Париж), французский астроном, геодезист и метролог. С 1792 член и с 1803 секретарь отделения математических наук Парижской АН. Совместно с П. Мешеном принимал (1792—97) участие в градусном измерении дуги меридиана от Дюнкерка до Барселоны, послужившем основанием для установления метрической системы мер . Д. вычислил таблицы видимых движений Солнца, больших планет и спутников Юпитера. Усовершенствовал методы астрономических вычислений. Написал 6-томную историю астрономии)

При решении засечки по формулам Деламбра нумерация исходных пунктов, а также углов должна производиться по часовой стрелке, при этом для нумерации углов должно быть выбрано начальное направление.

На рис. 5.1 показана схема обратной однократной засечки применительно к формулам Деламбра. В качестве исходных здесь используются три пункта триангуляции , и . Пункт – определяемый. Направление выбрано за начальное и от этого направления на пункте измерены углы и до направлений на пункты и .

Рисунок 5.1 – Схема обратной однократной угловой засечки

Для решения задачи первоначально по формуле Деламбра (формула дается без вывода) определяют дирекционный угол начального направления , принятого за начальное:

(5.1)

После определения дирекционного угла направления вычисляют дирекционные углы направлений и по формулам:

(5.2)

(5.3)

В итоге получим прямую угловую засечку с известными дирекционными углами направлений с определяемого пункта на исходные. В этом случае для определения координат , пункта достаточно использовать формулы Гаусса, выраженные через приращения координат исходных пунктов, а именно:

(5.4)

(5.5)

_(5.6)

(5.7)

Координаты определяемого пункта вычисляют дважды, что позволяет контролировать процесс вычисления. Кроме того, повторно вычисляют дирекционный угол по формуле:

(5.8)

Следует иметь в виду, что вычисленное по формуле (5.8) значение может отличаться от значения угла , вычисленного по формуле (5.2), на , так как знаки числителя и знаменателя в формуле (5.1) не определяют знаки приращений координат и . Для контроля вычисленного значения следует определить знаки и четверти по карте, на которой составлен проект вставки пунктов обратными засечками.

Следует также иметь в виду, что обратная угловая засечка по трем исходным пунктам не имеет решения, если определяемый пункт располагается на одной с исходными пунктами окружности, которую в этом случае называют «опасной» (рис.5.2). Доказано, что удаление определяемого пункта от «опасной» окружности на , обеспечивает надежное определение планового положения искомого пункта, где – радиус окружности.

При составлении на карте или плане схемы обратной засечки вставляемого пункта, очевидно, что если определяемый пункт находится внутри треугольника, в вершинах которого расположены исходные пункты, речи об «опасной» окружности быть не может.

В остальных случаях следует на карте или плане по правилам геометрии построить окружность, проходящую через три пункта, принимаемых за исходные. Тогда легко визуально определить область попадания определяемого пункта в «опасную» полосу.

Рисунок 5.2 – Схема «опасной» полосы в обратной засечке

Источник

Обратная угловая засечка в геодезических измерениях

Засечкой называют относительно простой метод вычисления координат некоторой точки посредством измерения на ней углов и расстояний по направлению на уже закрепленные на местности контуры.

К ней достаточно часто прибегают в различных геологических, строительных и инженерных работах за счет ее простоты и экономичности. На практике обратная засечка чаще всего используются для вычисления координат пунктов геодезической сети, выноса в натуру проектных точек и т.д.

Опытный геодезист сможет без труда провести нужные измерения при помощи теодолита, тахеометра или любого другого прибора всего за пару минут.

Виды засечек

В зависимости от местности и способов построения сетей сгущения в геодезии существует два основных вида привязки к опорным пунктам:

1. Непосредственная. Подразумевает привязку теодолитного или полигонометрического хода к триангуляционным пунктам высшего класса с возможностью выполнить измерения примычных углов. Используется в тех случаях, когда на опорных точках можно выполнить те же измерения, что и на соседних.
2. Косвенная. Проводится только при отсутствии возможности провести непосредственные измерения примычных длин и углов. К этому виду привязки и относится засечка.

По способу же построения геодезическая засечка бывает:

• линейной (полярные и биполярные по числу пунктов);
• угловой (прямая и обратная);
• комбинированной (положение точки определяют по известным углам и линейным расстояниям).

В геодезии чаще всего прибегают к комбинированию прямой и обратной засечек. Кроме того, чтобы полученные результаты были наиболее достоверными, измеряют больше величин, чем нужно, а само местоположение искомых пунктов получают посредством уравнивания.

Однократная и многократная засечка

Если для определения координат берется только один исходный пункт, то такая засечка будет называться однократной, а если более трех – многократной.

В основе обратной однократной угловой засечки лежит так называемая задача Потенота, которая была названа в честь французского математика Лорана Потенота, удачно решившего ее еще в 1692 году. Ученый предложил по известным значениям трех близлежащих точек вычислять координаты искомой.

На сегодняшний день существует уже более ста вариаций ее решения, которые были предложены многими именитыми учеными, но в геодезической практике наибольшую популярность получили формулы Жана Деламбра, Кнейссля и Гаусса.

Рисунок 1. Обратная многократная засечка

Важно отметить, что достоверные данные удается получить только в тех случаях, когда искомая точка находится в пределах треугольника, который образовали исходные пункты или же вне его, но напротив одной из его вершин.

Если же искомая точка попадает в пределы окружности, проходящей через эти точки, она становится неопределяемой. Этот ключевой недостаток в задаче Потенота, именуемый опасным кругом, приводит к необходимости определения дополнительной точки.

Обратная многократная угловая засечка как раз и подразумевает определение местоположения пункта через измерения на этом самом пункте углов или направлений как минимум на четыре твердых пункта, чьи координаты установлены. Этот метод более трудоемкий, но гарантирует надежный контроль результатов измерений. При обработке данных используют метод Гаусса-Ньютона, который в геодезии также называют параметрическим.

Способ Деламбра

Решение обратной засечки при помощи этого способа выполняется в такой последовательности:

Вычисляется дирекционный угол исходного направления с отметки 1 на точку «0» по формуле обратной геодезической засечки:

Значения дирекционных углов с исходных отметок Т2, Т3, Т4 получают из формул:

Находят координаты точки Р с помощью формул тангенсов или котангенсов дирекционных углов направлений.

Способ Кнейссля

Аналогично способу Деламбра последовательность формул при решении задачи обратной геодезической засечки по Кнейсслю будет иметь следующий вид:

Определяются вспомогательные коэффициенты:

Вычисляется котангенс дирекционного угла исходного направления на заданный пункт:

Приращения координаты точки Р относительно исходного пункта 1 находят при помощи нижеприведенных формул:

\(\Delta x_<1-p>=c\cdot \Delta y_<1-p>\)

Определяются координаты точки Р:

\(y_

=y_<1>+\Delta y_<1-p>\)

Средняя квадратическая погрешность вычисления местоположения пункта Р по трем направлениям вычисляется при помощи выражения:

Оценивается точность обратной угловой засечки по способу Кнейссля с определением погрешности:

Допустимость в расхождениях полученных значений двух вариантов решений выполняется по формуле:

Если данное условие соблюдено, то итоговое значение координат берется как среднее арифметическое значение из результатов двух решений.

Уравнивание при помощи параметрического способа

Под определение обратной многократной угловой засечки попадает как совокупность простых однократных измерений, так и просто большое количество избыточных. Однако в обоих случаях необходимо уравнивание, которое выполняется по измеренным углам и направлениям.

К примеру, неизвестные \(x_

\) и \(y_

\) – координаты точки Р, которые в данном способе будут представлены в качестве параметров. Для этого их представляют в виде приближенных значений \(x_<0>\), \(y_<0>\) и поправок к ним \(δх\) и \(δу\).

В приведенном уравнении \(x_<0>\) и \(y_<0>\) – результаты обработки однократных засечек, а \(δх\) и \(δу\) получают через уравнивание методом наименьших квадратов параметрическим способом с применением дифференциальных формул.

Этот метод подразумевает применение не только параметрического, но и коррелатного способа. Они дают одинаковые результаты, но отличаются по объему вычислений.

Однако в геодезической практике целесообразнее применять параметрический способ, поскольку при любом количестве избыточных измерений число нормальных уравнений будет аналогично числу неизвестных. При этом каждое неизвестное будет представлено в виде суммы приближенного значения и его поправки.

Сферы применения

Обратная угловая засечка нашла широкое применение в строительстве высотных зданий и сооружений, вроде опорных конструкций для мостов и дымовых труб. Кроем того, она позволяет быстро построить строительную сетку или определить местоположение точки в пространстве. В геодезии ее нередко используют в трилатерации и триангуляции.

Нельзя также не упомянуть ее огромного практического значения в навигации и военном деле. В частности, засечка по обратным дирекционным углам используется для топографогеодезической подготовки командно-наблюдательного пункта и позиции ведения огня.

Источник