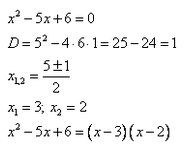- Метод интервалов, решение неравенств
- Определение квадратного неравенства
- Решение неравенства графическим методом
- Решение неравенства методом интервалов
- Плюс или минус: как определить знаки
- Решение квадратных неравенств графически
- Суть графического метода
- Решение с двумя корнями у квадратного трехчлена
- Решение с одним корнем у квадратного трехчлена
- Решение квадратного трехчлена, не имеющего корней
- Алгоритм решения неравенств с использованием графического способа
Метод интервалов, решение неравенств
О чем эта статья:
Определение квадратного неравенства
Неравенство — алгебраическое выражение, в котором используются знаки ≠, , ≤, ≥.
Числовое неравенство — это такое неравенство, в записи которого по обе стороны от знака находятся числа или числовые выражения.
Решение — значение переменной, при котором неравенство становится верным.
Решить неравенство значит найти множество, для которых оно выполняется.
Квадратное неравенство выглядит так:
 |
где x — переменная,
Квадратное неравенство можно решить двумя способами:
- графический метод;
- метод интервалов.
Решение неравенства графическим методом
При решении квадратного неравенства необходимо найти корни соответствующего квадратного уравнения ax^2 + bx + c = 0. Чтобы найти корни, нужно найти дискриминант данного уравнения.
Как дискриминант влияет на корни уравнения:
- D = 0. Если дискриминант равен нулю, тогда у квадратного уравнения есть один корень;
- D > 0. Если дискриминант больше нуля, тогда у квадратного уравнения есть два корня;
- D
Решение неравенства методом интервалов
Метод интервалов — это специальный алгоритм, который предназначен для решения рациональных неравенств.
Рациональное неравенство имеет вид f(x) ≤ 0, где f(x) — рациональная функция. При этом знак может быть любым: >, или ≥ — наносим штриховку над промежутками со знаками +.
Если неравенство со знаком
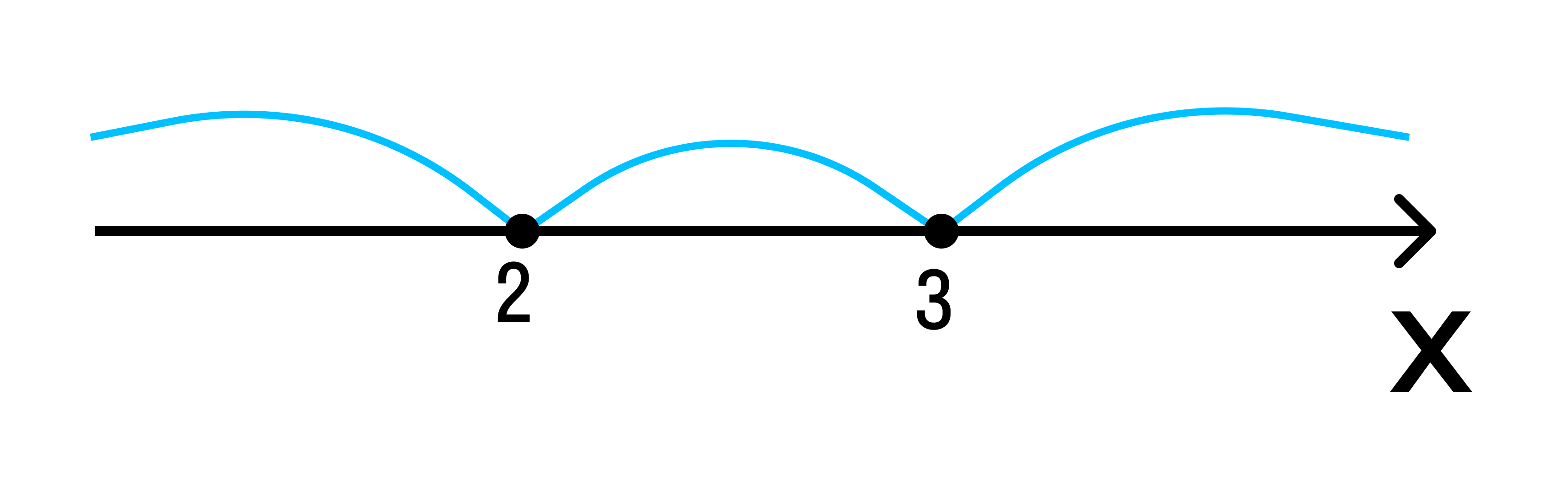
Отобразим эти данные на чертеже:
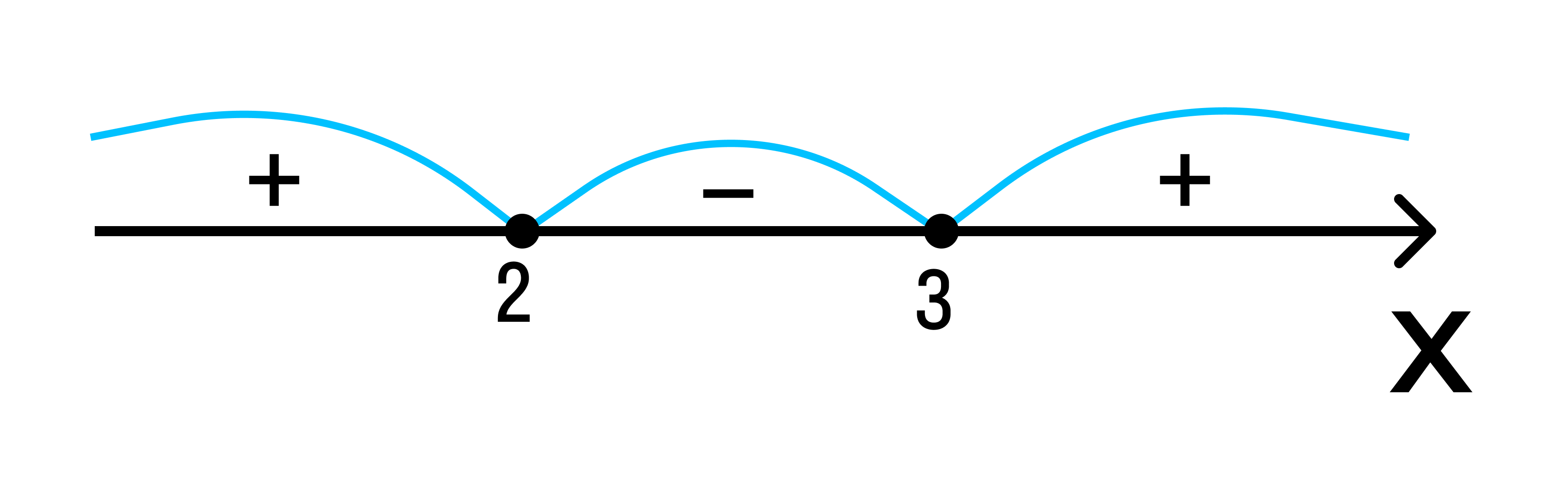
2 3 — на этом интервале ситуация не изменяется. Значит нужно взять любое значение из этого интервала и подставить его в произведение. Например: х = 25.
- (25 — 3) (25 — 2) = 22*23 = 506 > 0
Вывод: при х > 3 верно неравенство (х — 3) * (х — 2) > 0. Внесем эти данные в чертеж.
Исходное неравенство: (х — 3) * (х — 2) ≥ 0.
Если (х — 3) * (х — 2) > 0:
Если (х — 3) (х — 2) = 0 — при х1 = 3, х2 = 2.
Удовлетворяющие неравенству точки закрасим, а не удовлетворяющие — оставим пустыми.

Ответ: х ≤ 0, х ≥ 3.
Пример 2. Применить метод интервалов для решения неравенства х2+4х+3
Источник
Решение квадратных неравенств графически
Графический метод является одним из основных методов решения квадратных неравенств. В статье мы приведем алгоритм применения графического метода, а затем рассмотрим частные случаи на примерах.
Суть графического метода
Метод применим для решения любых неравенств, не только квадратных. Суть его вот в чем: правую и левую части неравенства рассматривают как две отдельные функции y = f ( x ) и y = g ( x ) , их графики строят в прямоугольной системе координат и смотрят, какой из графиков располагается выше другого, и на каких промежутках. Оцениваются промежутки следующим образом:
- решениями неравенства f ( x ) > g ( x ) являются интервалы, где график функции f выше графика функции g ;
- решениями неравенства f ( x ) ≥ g ( x ) являются интервалы, где график функции f не ниже графика функции g ;
- решениями неравенства f ( x ) g ( x ) являются интервалы, где график функции f ниже графика функции g ;
- решениями неравенства f ( x ) ≤ g ( x ) являются интервалы, где график функции f не выше графика функции g ;
- абсциссы точек пересечения графиков функций f и g являются решениями уравнения f ( x ) = g ( x ) .
Рассмотрим приведенный выше алгоритм на примере. Для этого возьмем квадратное неравенство a · x 2 + b · x + c 0 ( ≤ , > , ≥ ) и выведем из него две функции. Левая часть неравенства будет отвечать y = a · x 2 + b · x + c (при этом f ( x ) = a · x 2 + b · x + c ) , а правая y = 0 (при этом g ( x ) = 0 ).
Графиком первой функции является парабола, второй прямая линия, которая совпадает с осью абсцисс О х . Проанализируем положение параболы относительно оси О х . Для этого выполним схематический рисунок.
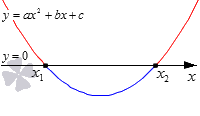
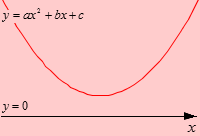
Решение с двумя корнями у квадратного трехчлена
Ветви параболы направлены вверх. Она пересекает ось О х в точках x 1 и x 2 . Коэффициент а в данном случае положительный, так как именно он отвечает за направление ветвей параболы. Дискриминант положителен, что указывает на наличие двух корней у квадратного трехчлена a · x 2 + b · x + c . Корни трехчлена мы обозначили как x 1 и x 2 , причем приняли, что x 1 x 2 , так как на оси О х изобразили точку с абсциссой x 1 левее точки с абсциссой x 2 .
Части параболы, расположенные выше оси О х обозначим красным, ниже – синим. Это позволит нам сделать рисунок более наглядным.
Выделим промежутки, которые соответствуют этим частям и отметим их на рисунке полями определенного цвета.
Красным мы отметили промежутки ( − ∞ , x 1 ) и ( x 2 , + ∞ ) , на них парабола выше оси О х . Они являются решением квадратного неравенства a · x 2 + b · x + c > 0 . Синим мы отметили промежуток ( x 1 , x 2 ) , который является решением неравенства a · x 2 + b · x + c 0 . Числа x 1 и x 2 будут отвечать равенству a · x 2 + b · x + c = 0 .
Сделаем краткую запись решения. При a > 0 и D = b 2 − 4 · a · c > 0 (или D ‘ = D 4 > 0 при четном коэффициенте b ) мы получаем:
- решением квадратного неравенства a · x 2 + b · x + c > 0 является ( − ∞ , x 1 ) ∪ ( x 2 , + ∞ ) или в другой записи x x 1 , x > x 2 ;
- решением квадратного неравенства a · x 2 + b · x + c ≥ 0 является ( − ∞ , x 1 ] ∪ [ x 2 , + ∞ ) или в другой записи x ≤ x 1 , x ≥ x 2 ;
- решением квадратного неравенства a · x 2 + b · x + c 0 является ( x 1 , x 2 ) или в другой записи x 1 x x 2 ;
- решением квадратного неравенства a · x 2 + b · x + c ≤ 0 является [ x 1 , x 2 ] или в другой записи x 1 ≤ x ≤ x 2 ,
где x 1 и x 2 – корни квадратного трехчлена a · x 2 + b · x + c , причем x 1 x 2 .
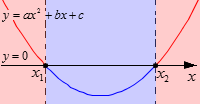
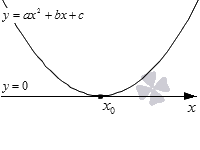
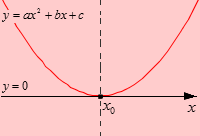
Решение с одним корнем у квадратного трехчлена
На данном рисунке парабола касается оси O х только в одной точке, которая обозначена как x 0 . Ветви параболы направлены вверх, что означает, что a > 0 . D = 0 , следовательно, квадратный трехчлен имеет один корень x 0 .
Парабола расположена выше оси O х полностью, за исключением точки касания координатной оси. Обозначим цветом промежутки ( − ∞ , x 0 ) , ( x 0 , ∞ ) .
Запишем результаты. При a > 0 и D = 0 :
- решением квадратного неравенства a · x 2 + b · x + c > 0 является ( − ∞ , x 0 ) ∪ ( x 0 , + ∞ ) или в другой записи x ≠ x 0 ;
- решением квадратного неравенства a · x 2 + b · x + c ≥ 0 является ( − ∞ , + ∞ ) или в другой записи x ∈ R ;
- квадратное неравенство a · x 2 + b · x + c 0 не имеет решений (нет интервалов, на которых парабола расположена ниже оси O x );
- квадратное неравенство a · x 2 + b · x + c ≤ 0 имеет единственное решение x = x 0 (его дает точка касания),
где x 0 — корень квадратного трехчлена a · x 2 + b · x + c .
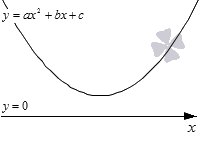
Решение квадратного трехчлена, не имеющего корней
Рассмотрим третий случай, когда ветви параболы направлены вверх и не касаются оси O x . Ветви параболы направлены вверх, что означает, что a > 0 . Квадратный трехчлен не имеет действительных корней, так как D 0 .
На графике нет интервалов, на которых парабола была бы ниже оси абсцисс. Это мы будем учитывать при выборе цвета для нашего рисунка.
Получается, что при a > 0 и D 0 решением квадратных неравенств a · x 2 + b · x + c > 0 и a · x 2 + b · x + c ≥ 0 является множество всех действительных чисел, а неравенства a · x 2 + b · x + c 0 и a · x 2 + b · x + c ≤ 0 не имеют решений.
Нам осталось рассмотреть три варианта, когда ветви параболы направлены вниз. На этих трех вариантах можно не останавливаться подробно, так как при умножении обеих частей неравенства на − 1 мы получаем равносильное неравенство с положительным коэффициентом при х 2 .
Алгоритм решения неравенств с использованием графического способа
Рассмотрение предыдущего раздела статьи подготовило нас к восприятию алгоритма решения неравенств с использованием графического способа. Для проведения вычислений нам необходимо будет каждый раз использовать чертеж, на котором будет изображена координатная прямая O х и парабола, которая отвечает квадратичной функции y = a · x 2 + b · x + c . Ось O у мы в большинстве случаев изображать не будем, так как для вычислений она не нужна и будет лишь перегружать чертеж.
Для построения параболы нам необходимо будет знать две вещи:
- направление ветвей, которое определяется значением коэффициента a ;
- наличие точек пересечения параболы и оси абсцисс, которые определяются значением дискриминанта квадратного трехчлена a · x 2 + b · x + c .
Точки пересечения и касания мы будет обозначать обычным способом при решении нестрогих неравенств и пустыми при решении строгих.
Наличие готового чертежа позволяет перейти к следующему шагу решения. Он предполагает определение промежутков, на которых парабола располагается выше или ниже оси O х . Промежутки и точки пересечения и являются решением квадратного неравенства. Если точек пересечения или касания нет и нет интервалов, то считается, что заданное в условиях задачи неравенство не имеет решений.
Теперь решим несколько квадратных неравенств, используя приведенный выше алгоритм.
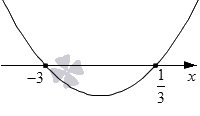
Необходимо решить неравенство 2 · x 2 + 5 1 3 · x — 2 графическим способом.
Решение
Нарисуем график квадратичной функции y = 2 · x 2 + 5 1 3 · x — 2 . Коэффициент при x 2 положительный, так как равен 2 . Это значит, что ветви параболы будут направлены вверх.
Вычислим дискриминант квадратного трехчлена 2 · x 2 + 5 1 3 · x — 2 для того, чтобы выяснить, имеет ли парабола с осью абсцисс общие точки. Получаем:
D = 5 1 3 2 — 4 · 2 · ( — 2 ) = 400 9
Как видим, D больше нуля, следовательно, у нас есть две точки пересечения: x 1 = — 5 1 3 — 400 9 2 · 2 и x 2 = — 5 1 3 + 400 9 2 · 2 , то есть, x 1 = − 3 и x 2 = 1 3 .
Мы решаем нестрогое неравенство, следовательно проставляем на графике обычные точки. Рисуем параболу. Как видите, рисунок имеет такой же вид как и в первом рассмотренном нами шаблоне.
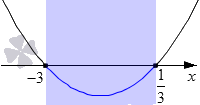
Наше неравенство имеет знак ≤ . Следовательно, нам нужно выделить промежутки на графике, на которых парабола расположена ниже оси O x и добавить к ним точки пересечения.
Нужный нам интервал − 3 , 1 3 . Добавляем к нему точки пересечения и получаем числовой отрезок − 3 , 1 3 . Это и есть решение нашей задачи. Записать ответ можно в виде двойного неравенства: − 3 ≤ x ≤ 1 3 .
Ответ: − 3 , 1 3 или − 3 ≤ x ≤ 1 3 .
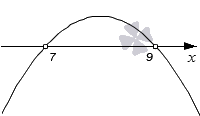
Решите квадратное неравенство − x 2 + 16 · x − 63 0 графическим методом.
Решение
Квадрат переменной имеет отрицательный числовой коэффициент, поэтому ветви параболы будут направлены вниз. Вычислим четвертую часть дискриминанта D ‘ = 8 2 − ( − 1 ) · ( − 63 ) = 64 − 63 = 1 . Такой результат подсказывает нам, что точек пересечения будет две.
Вычислим корни квадратного трехчлена: x 1 = — 8 + 1 — 1 и x 2 = — 8 — 1 — 1 , x 1 = 7 и x 2 = 9 .
Получается, что парабола пересекает ось абсцисс в точках 7 и 9 . Отметим эти точки на графике пустыми, так как мы работаем со строгим неравенством. После этого нарисуем параболу, которая пересекает ось O х в отмеченных точках.
Нас будут интересовать промежутки, на которых парабола располагается ниже оси O х . Отметим эти интервалы синим цветом.
Получаем ответ: решением неравенства являются промежутки ( − ∞ , 7 ) , ( 9 , + ∞ ) .
Ответ: ( − ∞ , 7 ) ∪ ( 9 , + ∞ ) или в другой записи x 7 , x > 9 .
В тех случаях, когда дискриминант квадратного трехчлена равен нулю, необходимо внимательно подходить к вопросу о том, стоит ли включать в ответ абсциссы точки касания. Для того, чтобы принять правильное решение, необходимо учитывать знак неравенства. В строгих неравенствах точка касания оси абсцисс не является решением неравенства, в нестрогих является.
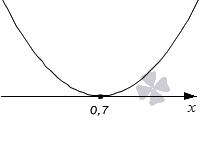
Решите квадратное неравенство 10 · x 2 − 14 · x + 4 , 9 ≤ 0 графическим методом.
Решение
Ветви параболы в данном случае будут направлены вверх. Она будет касаться оси O х в точке 0 , 7 , так как
Построим график функции y = 10 · x 2 − 14 · x + 4 , 9 . Ее ветви направлены вверх, так как коэффициент при x 2 положительный, и она касается оси абсцисс в точке с абсциссой 0 , 7 , так как D ‘ = ( − 7 ) 2 − 10 · 4 , 9 = 0 , откуда x 0 = 7 10 или 0 , 7 .
Поставим точку и нарисуем параболу.
Мы решаем нестрогое неравенство со знаком ≤ . Следовательно. Нас будут интересовать промежутки, на которых парабола располагается ниже оси абсцисс и точка касания. На рисунке нет интервалов, которые удовлетворяли бы нашим условиям. Есть лишь точка касания 0 , 7 . Это и есть искомое решение.
Ответ: Неравенство имеет только одно решение 0 , 7 .
Решите квадратное неравенство – x 2 + 8 · x − 16 0 .
Решение
Ветви параболы направлены вниз. Дискриминант равен нулю. Точка пересечения x 0 = 4 .
Отмечаем точку касания на оси абсцисс и рисуем параболу.
Мы имеем дело со строгим неравенством. Следовательно, нас интересуют интервалы, на которых парабола расположена ниже оси O х . Отметим их синим.
Точка с абсциссой 4 не является решением, так как в ней парабола не расположена ниже оси O x . Следовательно, мы получаем два интервала ( − ∞ , 4 ) , ( 4 , + ∞ ) .
Ответ: ( − ∞ , 4 ) ∪ ( 4 , + ∞ ) или в другой записи x ≠ 4 .
Не всегда при отрицательном значении дискриминанта неравенство не будет иметь решений. Есть случаи, когда решением будет являться множество всех действительных чисел.
Решите квадратное неравенство 3 · x 2 + 1 > 0 графическим способом.
Решение
Коэффициент а положительный. Дискриминант отрицательный. Ветви параболы будут направлены вверх. Точек пересечения параболы с осью O х нет. Обратимся к рисунку.
Мы работаем со строгим неравенством, которое имеет знак > . Это значит, что нас интересуют промежутки, на которых парабола располагается выше оси абсцисс. Это как раз тот случай, когда ответом является множество всех действительный чисел.
Ответ: ( − ∞ , + ∞ ) или так x ∈ R .
Необходимо найти решение неравенства − 2 · x 2 − 7 · x − 12 ≥ 0 графическим способом.
Решение
Ветви параболы направлены вниз. Дискриминант отрицательный, следовательно, общих точек параболы и оси абсцисс нет. Обратимся к рисунку.
Мы работаем с нестрогим неравенством со знаком ≥ , следовательно, интерес для нас представляют промежутки, на которых парабола располагается выше оси абсцисс. Судя по графику, таких промежутков нет. Это значит, что данное у условии задачи неравенство не имеет решений.
Источник