Решение неравенств с двумя переменными графическим способом 9 класс

Неравенство с двумя переменными и его решение: значение, список примеров

Содержание:

Линейное неравенство, имеющее две переменных; его функция имеет общий вид ах + bу + с меньше нулевого значения или больше 0. В качестве переменных выступают у, х. Для обозначения некоторых чисел используются буквы а, b, с. Решение неравенств с двумя переменными графическим способом предполагает использование плоскости координат. Задача – найти пару чисел, которая сделает пример верным равенством.

Неравенство с двумя неизвестными – сложный линейный пример, требующий построения графика. В большинстве случаев имеет множество вариантов решения. Например, заданы числа 2 и 1, необходимо решить выражение 5х + 2у > 4. Для этого следует подставить данные коэффициенты в пример. В итоге получается: 5*2 + 2*1 > 4, 10 + 2 больше 4. Решение допустимое.

Более легкий способ решить уравнение – построить графическую координатную плоскость. Внешний вид решения имеет определенную фигуру.

График неравенства с двумя переменными – решение

Функция имеет следующее определение: 3х — 2у + 6 > 0. Нужно определить точки на плоскости, которые подойдут для решения примера. Если 3х -2у + 6 > 0 приравнять к нулю, получится 3х — 2у + 6 = 0. Это стандартное обозначение прямой, проходящей через две области: -2,0 и 0,-3. Относим коэффициенты к области М1(Х1,У1). Эта зона заштриховывается на плоскости, она находится под 3х — 2у + 6 = 0 – прямой.

Коэффициенты М2(Х₂,У₂) попадают на прямую. Отсюда следует: 2у₂ — 3х₁ — 6 = 0, 2у₁ — 3х₁ — 6 0. Изначально строится прямая. В качестве решения выступает набор точек, расположенных над или под прямой. Чтобы понять, какая плоскость является ответом, необходимо выполнить подстановку значений в уравнение.

Графическое решение неравенств с двумя переменными – пример

Большинство неравенств с двумя неизвестными решаются графически. Необходимо выбрать, какой метод для поиска решения лучше применить. Координатная плоскость позволяет сделать рисунок, наглядно увидеть ответ. Задача – поиск двух коэффициентов, удовлетворяющих требованиям примера. Рассмотрим выражение 2у + 3х

Источник

Графическое решение неравенств с двумя переменными
презентация к уроку по алгебре (9 класс) на тему

Урок-объяснение нового материала- «Графическое решение неравенств, систем неравенств с двумя переменными.», в 9 классе, с углубленным изучением математики.

Скачать:

Вложение	Размер
neravenstva.rar	217.38 КБ

Предварительный просмотр:

Урок алгебры в 9 классе

Графическое решение неравенств, систем неравенств с двумя переменными.

Учитель математики Прокофьева И.Л.

МБОУ лицей №8 г. Ставрополь

Цели и задачи урока:

1. Ввести понятие системы неравенств с двумя переменными.

Составить алгоритм решения систем неравенств

Формировать навыки решения систем неравенств

2. Развивать « критическое» мышление и интерес к предмету у учащихся в процессе решения проблемных ситуаций и заданий творческого характера.

Оборудование: Ноутбук , мультимедийный проектор,

• Организация начала занятия.
• Проверка выполнения домашнего задания.
• Подготовка к усвоению новых знаний.
• Изучение нового материала.
• Первичная проверка знаний.
• Закрепление знаний.
• Подведение итогов занятий.
• Домашнее задание.

Ход урока. 1. Организационный момент.

На предыдущих уроках мы решали системы уравнений графическим способом. Сегодня мы переходим к изучению новой темы «Графическое решение неравенств, систем неравенств с двумя переменными». Повторим материал прошлого урока.

1. Устная работа учащихся с использованием проектора.

Из данных 6 функций выберите те, которые будут изображаться на экране.

Даны функции (записаны на доске)

• 

3 .Изучение новой темы .

Неравенство с двумя неизвестными можно представить так: f(x;y) > , где f(x;y), – многочлен двух переменных х и у . Его можно записать в виде .

Неравенства содержащие неизвестные могут быть вида

F(x,y) 0, F(x,y) 0, F(x,y) 0.

• Решением неравенства называется упорядоченная пара действительных чисел , обращающая это неравенство в верное числовое неравенство.
• Графически это соответствует заданию точки координатной плоскости.
• Решить неравенство — значит найти множество его решений

Если одно из неравенств системы представлено в виде нестрогого неравенства, то график изображается сплошной линией, если строгое, то пунктирной.

Если одно из неравенств системы представлено в виде у ≥f(x). То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если одно из неравенств системы представлено в виде у ≤f(x). То это неравенство задает на плоскости область, которая лежит не ниже графика.

Если линия f(x.у)- замкнутая, например окружность, или замкнутая ломанная , то неравенство f(x.у≥0, задает область лежащую внутри замкнутой линии., а неравенство f(x.у)≤0 — область лежащую вне.

И наиболее универсальное, полезное для проверки правило- Правило пробной точки

• Построить F(x;y)=0
• Взяв из какой — либо области пробную точку установить, являются ли ее координаты решением неравенства
• Сделать вывод о решении неравенства

Рассмотрим многочлен F(x;y)=y+x-1, тогда

В следующем примере дано уравнение окружности.

Необходимо расставить знаки неравенств >, ,используя правило пробной точки О(0,0).

1. Решить неравенство:│х-0,5│-1,5≤0
2. Решить неравенство:
3. Решить неравенство:

Системой неравенств с двумя переменными является система вида.

Алгоритм решения систем неравенств.

• Построить F(x;y)=0 и G(x;y)=0
• Взяв из каждой области пробную точку установить, являются ли ее координаты решением системы

Объединение полученных областей- решение системы неравенств

• Решаем вместе .

1. Решить систему неравенств:

2. Решить систему неравенств:

3 Решить графически неравенство:

Подведение итогов урока. Домашнее задание.

1. Ю.Н.МакарычевН.Г.Миндюк, К.Н.Нешков Алгебра. 9кл. учебник для класса с углубленным изучением математики Изд. Мнемозина, 2004-2006
2. Мордкович А.Г. . Алгебра, 9 кл. Учебник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
3. Мордкович А.Г. . Алгебра, 9 кл. Задачник для классов с углубленным изучением математики. Изд. Мнемозина, 2004-2006
4. А. Корянов Неравенства с двумя переменными: графическое и аналитическое решения Библиотека «Первого сентября, серия «Математика», выпуск 22,Москва, Чистые пруды,2008

По теме: методические разработки, презентации и конспекты

Презентация по теме «Решение неравенств с двумя переменными»

Данная презентация наглядно показывает графический способ решения неравенств с двумя переменными.

«Графическое решение уравнений с двумя переменными»

Урок по теме «Графическое решение уравнений с двумя переменными» разработан для учащихся 7 классов по программе учебника «Алгебра 7» Ю.Н. Макарычев, Н.Г. Миндюк и др. под ред. С.А. Теляковского.

Графическое решение неравенств c одной переменной. Графический способ решения систем уравнений.

Алгебра. Повторение. Подготовка к ГИА. 9 класс.

Решение неравенств и систем неравенств с двумя переменными

Алгебра.Повторение. Подготовка к ГИА. 9 класс.

Уравнения и неравенства с двумя переменными и их геометрическое решение

Разработка комплекса уроков содержит задания, аналитическое и графическое решения.Предназначена для подготовки к ЕГЭ.

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем

Метод интервалов. Изображение на координатной плоскости множества решений уравнений и неравенств с двумя переменными и их систем.

Графическое решение неравенств с двумя переменными

Графическое решение неравенств с двумя переменными.

Источник

Линейные неравенства с двумя переменными и их системы

Линейное неравенство с двумя переменными и его решение

Неравенство вида ax+by $ \begin \lt \\ \gt \\ \le \\ \ge \end $ c , где a, b, c — данные числа, называется линейным неравенством с двумя переменными x и y.

Например: $2x+5y \lt 6; -x+1, 5y \ge 0; \frac<1> <2>x-8y \gt 7$

Решением неравенства с двумя переменными называется упорядоченная пара значений переменных (x,y), обращающая это неравенство в истинное выражение.

Например: для неравенства $2x+5y \lt 6$

пара (-1;-2) является решением, т.к. $2\cdot(-1)+5 \cdot (-2) = -12 \lt 6$ – истина

пара (1;2) не является решением, т.к. $2\cdot1+5\cdot2=12 \not\lt 6$ – ложь

Графическое представление линейного неравенства с двумя переменными

Графическим представлением линейного неравенства с двумя переменными вида ax+by$ \begin \lt \\ \gt \\ \le \\ \ge \end $ c является полуплоскость с границей ax+by = c .

Для строгого неравенства граница не входит в представление, для нестрогого неравенства – входит.

Графическое решение системы линейных неравенств с двумя переменными

Графическим решением системы линейных неравенств с двумя переменными является пересечение их графических представлений на плоскости.

Пересечение двух множеств – это множество, которому принадлежат только те элементы, которые одновременно входят в оба множества.

Пересечение обозначают знаком $\cap$.

Найдём графическое решение системы линейных неравенств:

Решением является треугольник ABC, где A(-1;2), B(0;4), C(2;0).

Примеры

Пример 1. Найдите графическое представление линейного неравенства:

Представление – полуплоскость под границей, сама граница не входит

Представление – полуплоскость под границей, сама граница входит

Представление – полуплоскость справа от границы, сама граница входит

Представление – полуплоскость под границей, сама граница не входит

Пример 2*. Найдите графическое решение системы линейных неравенств:

Решением является квадрат ABCD, где A(-3;-1), B(0;2), C(3;1), D(0;-4)

Пример 3*. Автоперевозчику поступил заказ на перевозку 30 т груза. У него есть 5 машин грузоподъёмностью 3 т и 5 машин грузоподъёмностью 5 т.

Расход топлива для каждого типа грузовиков соответственно 20 и 24 л, общий расход не должен превышать 170 л.

Подберите состав грузовиков для выполнения заказа.

Пусть x — количество грузовиков по 3т, y – по 5т.

По условию задачи:

$$ <\left\< \begin 3x+5y \ge 30 \\ 20x+24y \le 170 \\ x \le 5 \\ y \le 5 \end \right.> $$

Решением системы неравенств является заштрихованный треугольник. Единственным целочисленным решением является точка A(2;5) Таким образом, для выполнения заказа нужно 2 грузовика по 3т и 5 грузовиков по 5т.

Их суммарная грузоподъёмность: $3 \cdot 2+5 \cdot 5 = 31 \gt 30$ достаточна

Суммарный расход топлива: $ 20 \cdot 2+24 \cdot 5 = 160 \lt 170 $ не превышает лимит

Ответ: 2 грузовика по 3т и 5 грузовиков по 5т

Источник

Графическое решение систем неравенств с двумя переменными

В презентации на конкретных примерах представлен способ решения систем неравенств с двумя переменными на координатной плоскости. Материал предназначен для объяснения темы «Системы неравенств с двумя переменными».в 9 классе (Алгебра, 9 класс, автор Макарычев Ю.Н.)

Просмотр содержимого документа
«Графическое решение систем неравенств с двумя переменными»

с двумя переменными

К учебнику Ю.Н.Макарычева

Алгебра, 9 класс, Глава III §

Автор: Софронова Наталия Андреевна,

учитель математики высшей категории

МОУ «Упшинская основная общеобразовательная школа»

Оршанского района Республики Марий Эл

Решение системы неравенств

с двумя переменными

Решением системы неравенств с двумя переменными называется пара значений этих переменных, являющаяся как решением первого неравенства, так и второго неравенства системы.

Изображение множества решений неравенства с двумя переменными на координатной плоскости

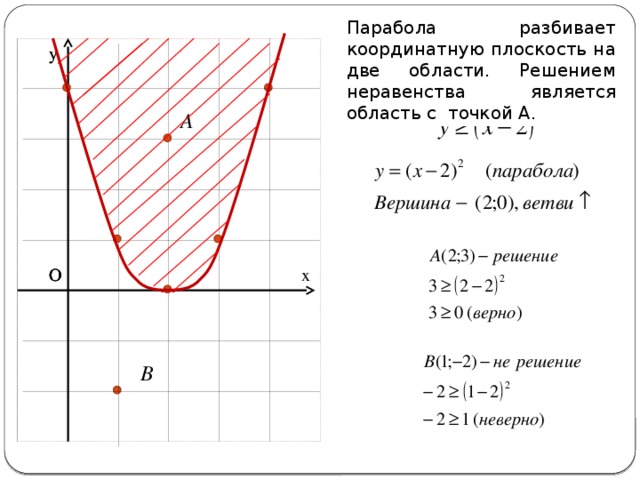
Парабола разбивает координатную плоскость на две области. Решением неравенства является область с точкой А.

Изображение множества решений системы неравенств с двумя переменными на координатной плоскости

Множеством решений системы неравенств с двумя переменными является пересечение множеств решений неравенств, входящих в систему. На координатной плоскости множество решений системы неравенств изображается множеством точек, являющихся общей частью множеств, представляющих собой решения каждого неравенства системы.

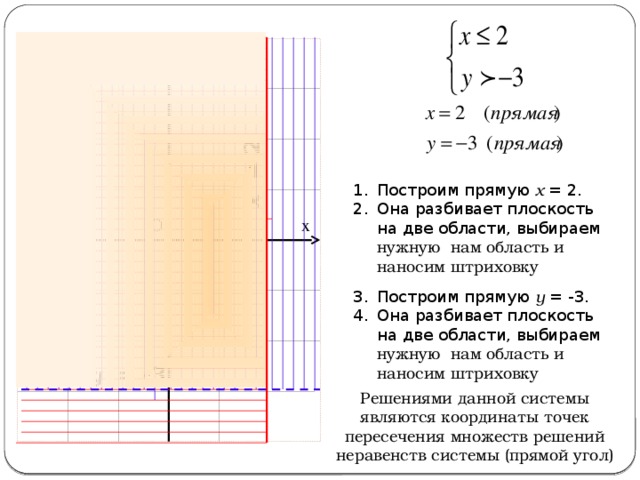
• Построим прямую х = 2.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = -3.
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (прямой угол)

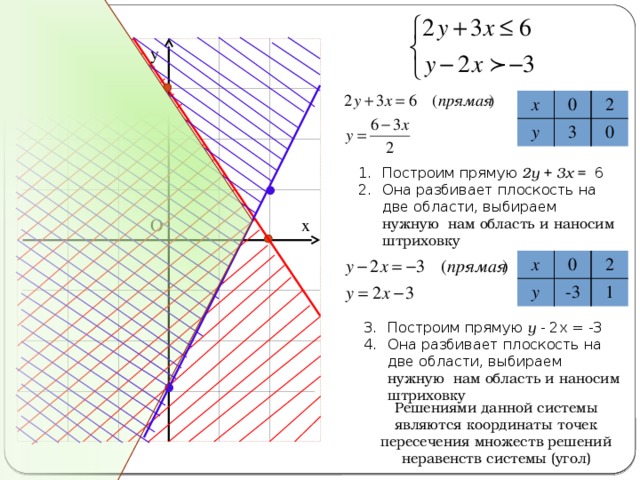
• Построим прямую 2у + 3х = 6
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у — 2х = -3
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (угол)

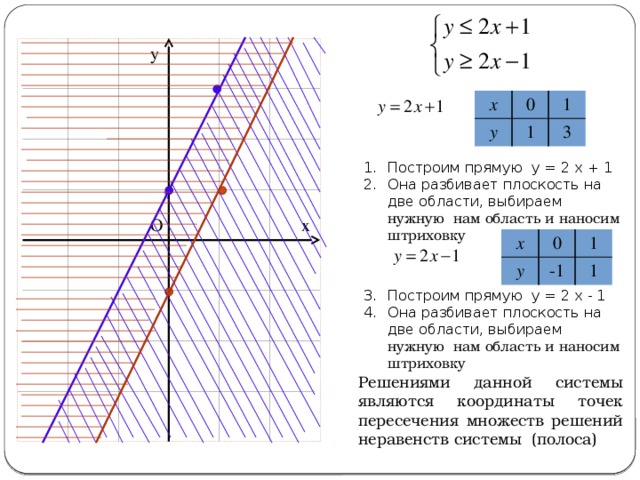
• Построим прямую у = 2 х + 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую у = 2 х — 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются координаты точек пересечения множеств решений неравенств системы (полоса)

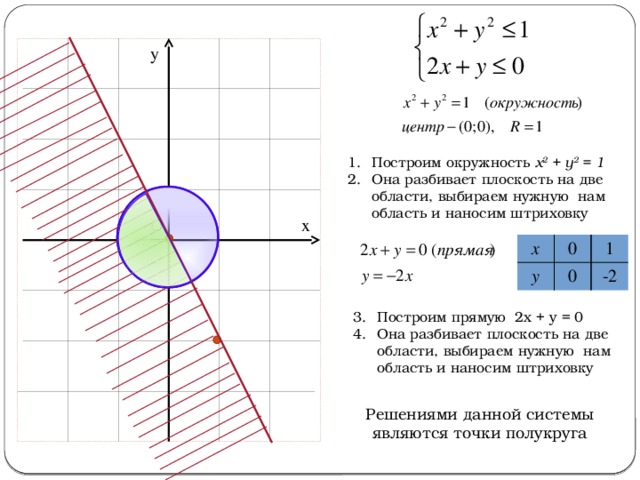
• Построим окружность х2+ у2= 1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим прямую 2х + у = 0
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки полукруга

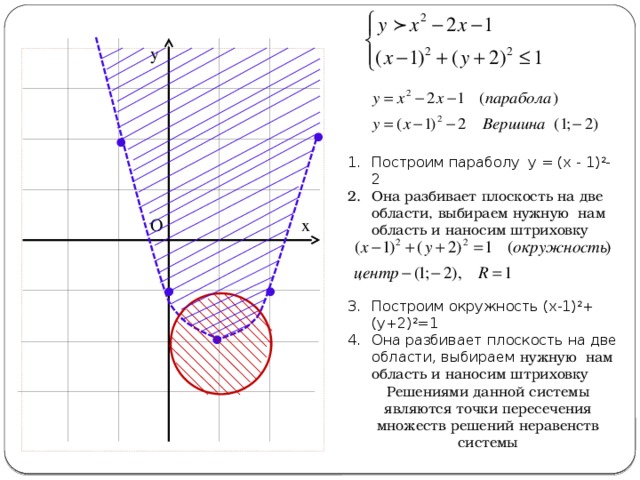
• Построим параболу у = (х — 1) 2 -2
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

• Построим окружность (х-1) 2 +(у+2) 2 =1
• Она разбивает плоскость на две области, выбираем нужную нам область и наносим штриховку

Решениями данной системы являются точки пересечения множеств решений неравенств системы

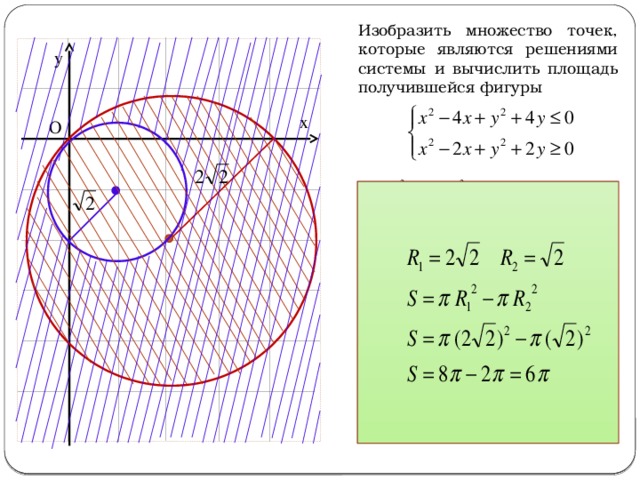
Изобразить множество точек, которые являются решениями системы и вычислить площадь получившейся фигуры

Источник