Проектная работа по математике НЕКОТОРЫЕ СПОСОБЫ РЕШЕНИЯ КВАДРАТНЫХ УРАВНЕНИЙ
Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Изучив решение квадратных уравнений, нам захотелось узнать, можно ли еще другими способами решить уравнение и в дальнейшем использовать различные способы при решении уравнений. Мы считаем эту тему актуальной, т. к. она может пригодиться нам не только во время обучения в школе, а впоследствии и в ВУЗе, и на протяжении всей жизни.
Скачать:
| Вложение | Размер |
|---|---|
| proekt8klass.doc | 709.5 КБ |
| kv._korni_prezentatsiya.pptx | 608.96 КБ |
Предварительный просмотр:
Муниципальное бюджетное общеобразовательное учреждение
«Серго-Ивановская основная школа»
Проектная работа по математике
НЕКОТОРЫЕ СПОСОБЫ РЕШЕНИЯ
Выполнили : Моисеева Юлия,
обучающиеся 8 класса
История развития теории и практики решения квадратных уравнений
Решение уравнений через дискриминант
По формуле с четным коэффициентом
Выделение полного квадрата двучлена.
Разложение на множители
Некоторые способы решения квадратных уравнений
Моисеева Юлия, Николаева Анна
Изучение различных способов решения квадратных уравнений
— изучить историю развития квадратных уравнений;
— рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
— выявить наиболее удобные способы решения квадратных уравнений;
— научиться решать квадратные уравнения различными способами.
Федорова Ирина Михайловна
Способы решения квадратного уравнения
Учебная тема (к которому ваш проект имеет отношение)
Тип проекта по предметно-содержательной характеристике:
При решении сформулированных задач была изучена специальная литература, собрана информация статистических данных для последующего использования в работе, проведено исследование по решению квадратного уравнения учащимися 8 классов с целью выявления различных способов решения квадратного уравнения.
Используемые информационные технологии: powerpoint, Microsoft Word;
Краткая аннотация проекта.
Большинство жизненных задач сводится к решению различных видов уравнений, и чаще это уравнения квадратного вида.
Изучив решение квадратных уравнений, нам захотелось узнать, можно ли еще другими способами решить уравнение и в дальнейшем использовать различные способы при решении уравнений. Мы считаем эту тему актуальной, т. к. она может пригодиться нам не только во время обучения в школе, а впоследствии и в ВУЗе, и на протяжении всей жизни.
Сроки реализации проекта
После завершения проекта мы будем:
· решать квадратные уравнения;
·выбирать наиболее рациональный способ решения квадратного уравнения;
· находить ошибки в решенных уравнениях и исправлять их;
·ориентироваться в информационной среде.
Практически все, что окружает современного человека — это все так или иначе связано с математикой. А последние достижения в физике, технике и информационных технологиях не оставляют никакого сомнения, что и в будущем положение вещей останется прежним. Поэтому решение многих практических задач сводится к решению различных видов уравнений, которые достаточно часто сводятся к уравнениям второй степени (квадратным).
В учебнике алгебры для 8 класса мы знакомимся с несколькими видами квадратных уравнений, и отрабатываем их решение по формулам. У меня возник вопрос «Существуют ли другие методы решения квадратных уравнений? Насколько сложны данные методы и можно ли ими пользоваться на практике?» Поэтому в этом учебном году я выбрал тему исследования связанную с квадратными уравнениями, в ходе работы она получила название «Некоторые способы решения квадратных уравнений».
Актуальность этой темы заключается в том, что на уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может мне пригодится при решении более сложных задач, в том числе и в 9 классе при сдаче экзаменов.
На уроках алгебры, геометрии, физики мы очень часто встречаемся с решением квадратных уравнений. Поэтому каждый ученик должен уметь верно и рационально решать квадратные уравнения, это также может пригодиться при решении более сложных задач, в том числе и при сдаче экзаменов.
Цель работы: Изучение различных способов решения квадратных уравнений
— изучить историю развития квадратных уравнений;
— рассмотреть стандартные и нестандартные методы решения квадратных уравнений;
— выявить наиболее удобные способы решения квадратных уравнений;
— научиться решать квадратные уравнения различными способами.
Гипотеза: любое квадратное уравнение можно решить всеми существующими способами.
Объект исследования: квадратные уравнения .
Предмет исследования: способы решения уравнений второй степени .
Уравнения — это наиболее объёмная тема всего курса математики.
Данная работа является попыткой обобщить и систематизировать изученный материал по выше указанной теме. В него вошли как известные нами из школьного курса алгебры способы решения квадратных уравнений, так и дополнительный материал.
История развития теории и практики решения квадратных уравнений
Необходимость решать уравнения не только первой, но и второй степени еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики.
В те далекие времена, когда мудрецы впервые стали задумываться о равенствах содержащих неизвестные величины, наверное, еще не было ни монет, ни кошельков. Но зато были кучи, а также горшки, корзины, которые прекрасно подходили на роль тайников-хранилищ, вмещающих неизвестное количество предметов. В древних математических задачах Междуречья, Индии, Китая, Греции неизвестные величины выражали число павлинов в саду, количество быков в стаде, совокупность вещей, учитываемых при разделе имущества. Хорошо обученные науке счета писцы, чиновники и посвященные в тайные знания жрецы довольно успешно справлялись с такими задачами.
Дошедшие до нас источники свидетельствуют, что древние ученые владели какими-то общими приемами решения задач с неизвестными величинами. Однако ни в одном папирусе, ни в одной глиняной табличке не дано описания этих приемов. Исключением является «Арифметика» греческого математика Диофанта Александрийского (III в.) — собрание задач на составление уравнений с систематическим изложением их решений.
Квадратные уравнения решали и в Индии. Древнеиндийский математик Баудхаяма впервые использовал квадратные уравнения в форме ax 2 = c и ax 2 + bx = c и привел методы их решения.
Уравнения второй степени умели решать еще в древнем Вавилоне. Математики Древней Греции решали квадратные уравнения геометрически; например, Евклид — при помощи деления отрезка в среднем и крайнем отношениях. Задачи, приводящие к квадратным уравнениям, рассматриваются во многих древних математических рукописях и трактах.
Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. в «Книге абака» итальянским математиком Леонардом Фибоначчи. Вывод формулы решения квадратного уравнения в общем виде имеется у Виета. Итальянские математики Тарталья, Кардано, Бомбелли среди первых в XVI в. учитывают, помимо положительных и отрицательные корни. Лишь в XVII в. благодаря трудам Жирара, Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный вид.
- Решение квадратных уравнений через дискриминант.
Корни уравнения ах 2 + bх + с = 0, а ≠ 0 можно найти по формуле
, где выражение b 2 — 4ac= D называется дискриминантом.
1. В случае положительного дискриминанта, т.е. при b 2 — 4ac>0, уравнение ах 2 + bх + с = 0 имеет два различных корня.
2. Если дискриминант равен нулю, т.е. b 2 — 4ac = 0 , то уравнение имеет один корень x= .
3. Если дискриминант отрицателен, т.е. b 2 — 4ac , квадратное уравнение ах 2 + bх + с = 0 не имеет корней.
Данная формула корней квадратного уравнения ах 2 + bх + с = 0 позволяет найти корни любого квадратного уравнения (если они есть), в том числе приведенного и неполного.
D= 4 2 — 4∙3∙ (-7) = 16 + 84 = 100,
- Решение квадратных уравнений по формуле с четным коэффициентом.
Если второй коэффициент уравнения b = 2k – четное число, то формулу корней можно записать в виде
Приведенное уравнение х 2 + рх + q= 0 совпадает с уравнением общего вида, в котором а = 1 , b = р и с = q . Поэтому для приведенного квадратного уравнения формула корней принимает вид
Формулу удобно использовать, когда р — четное число.
Источник
Исследовательская работа «Различные способы решения квадратных уравнений»
В школьном курсе математики изучаются формулы корней квадратных уравнений, с помощью которых можно решать любые квадратные уравнения.
Однако имеются и другие способы решения уравнений, которые позволяют очень быстро и рационально решать многие из них, что поможет мне при написании ОГЭ по математике где есть задания, связанные с темой «Квадратные уравнения».
По этому тему «Различные способы решения квадратных уравнений считаю актуальной.
Объект исследования: квадратные уравнения.
Предмет исследования: различные способы решения квадратных уравнений.
Содержимое разработки
МКОУ Тогучинского района «Дергоусовская средняя школа» Научно-практическая работа по математике по теме : «Различные способы решения квадратных уравнений»
Выполнила: ученица 8 класса Галузинская Анастасия
Руководитель: учитель математики Овчиникова Лариса Юрьевна
«Обезьянок резвых стая
Всласть поевши, развлекалась.
Их в квадрате часть восьмая
На поляне забавлялась.
А двенадцать по лианам…
Стали прыгать, повисая…
Сколько ж было обезьянок,
Ты скажи мне, в этой стае?»
Индийский математик XII в. Бхаскары
В основном государственном экзамене по математике есть задания, связанные с темой «Квадратные уравнения».
Объект исследования: квадратное уравнение.
различные способы решения
- Найти и изучить различные способы решения квадратных уравнений.
- Провести сравнительный анализ решения квадратных уравнений различными способами.
- Собрать информацию о различных способах решения квадратных уравнений;
- Освоить найденные способы решения;
- провести занятие «Быстрые способы решения квадратных уравнений» с учащимися 8 и 9 классов.
К вадратное уравнение можно решить разными способом.
называется уравнение вида
где х — переменная , а,b и с -некоторые числа, причем, а ≠0.
Если а=1 , — приведённое уравнение.
Если b=0 или с=0: =0 неполные
Методы решения квадратных уравнений излагались в вавилонских рукописях царя Хаммурапи XX в. до н. э.,
В древних китайских и японских
трактатах, в трудах древнегреческого
математика Евклида в III в. до н.э.
В III в. н. э. квадратное уравнение без обращения к геометрии решил великий древнегреческий математик Диофант .
Внесли большой вклад в решение квадратных уравнений великие математики
1. Разложение левой части на множители;
2. Метод выделения полного квадрата;
3. Применение формул корней квадратного уравнения;
4. С применением теоремы Виета;
5. Способом «переброски» коэффициентов;
6. Свойство делителя свободного члена;
7. Свойство коэффициентов квадратного уравнения;
8.Способ решения квадратных уравнений
по теореме Безу;
9. Графический способ;
10. С помощью циркуля и линейки;
11. Геометрический способ;
12. С помощью номограмм;
13. Решения квадратного уравнения с
1. Разложение левой части на множители
Решим уравнение : х 2 + 2х – 3 = 0.
Разложим левую часть уравнения на множители применяя способ группировки:
х 2 + 2х – 3 = х 2 + 3х – х – 3 = х (х + 3) – 1 (х +3) = (х + 3)(х – 1). Следовательно, уравнение можно переписать так:
Левая часть уравнения обращается в нуль при
х = -3, а также при х = 1.
2. Метод выделения полного квадрата
Решим уравнение х 2 + 2х – 3 = 0
Выделим в левой части полный квадрат.
х 2 + 2х – 3 = х 2 + 2· х ·1 + 1 2 – 1 2 – 3 = (х + 1) 2 – 1 – 3 =
Таким образом, данное уравнение можно записать так: (х + 1) 2 –4 = 0, т.е. (х + 1) 2 = 4.
Следовательно, х +1 = 2, х 1 = 1,
или х +1 = — 2 , х 2 = – 3.
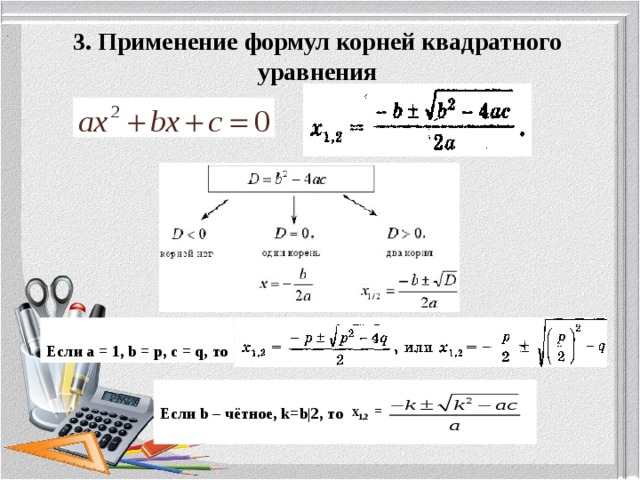
3. Применение формул корней квадратного уравнения
Если а = 1, b = p, c = q, то
Если b – чётное, k=b|2, то
4. С применением теоремы Виета
Теорема Виета для квадратного уравнения а х 2 + в х + с = 0, где х 1 и х 2 – корни уравнения, имеет вид:
Теорема Виета выполняется и для приведенного квадратного уравнения
х 2 + px + q = 0 и имеет вид:
х 2 – 3х + 2 = 0; p=-3, q = 2
Попробуем найти два числа х 1 и х 2 , такие, что
не трудно догадаться, что это числа х 1 = 2 и х 2 = 1
5. Способ «переброски» коэффициентов
Умножая обе части квадратного уравнения ах 2 + bх + с = 0 на а,
получаем уравнение а 2 х 2 + да а bх + ас = 0.
Обозначим ах через у, х =
, тогда приходим к уравнению у 2 + by + ас = 0
Его корни у 1 и у 2 найдем с помощью теоремы Виета.
Решим уравнение: 2х 2 – 11х + 15 = 0.
«Перебросим» коэффициент 2 к свободному члену, в результате
получим уравнение у 2 – 11 y + 30 = 0.
С помощью Теоремы Виета легко найти его корни
6. Свойство делителя свободного члена
Корень уравнения, если он есть целое число, является делителем свободного члена.
Рассмотрим на примере уравнения х 2 + 5х — 14 = 0.
Находим делители числа -14 начиная с меньших чисел, это
1, 2, 7, 14. Подставляя делители в уравнение получаем верное
равенство при делители равном 2, значит 2 – первый
По теореме Виета х 1* х 2 =с, значит, х 2 = -14/2 = -7.
7. Свойство коэффициентов квадратного уравнения
7. Если а + в = с, то корней нет
Решим уравнение: 2017х 2 – 2018х +1 = 0.
Так как 2017+ (-2018)+ 1= 0, то по свойству 1
8. Способ решения квадратных уравнений по теореме Безу
Если число n является корнем многочлена P(x), то этот многочлен делится на х — n без остатка.
Число n находим методом подбора делителя свободного члена и выполняя деление многочлена х — n на многочлен P(x) , получаем: (х – n)(х – m) = 0, где n и m -корни уравнения.
Решим уравнение: х 2 + 2х – 3 = 0,
Меньший делитель свободного члена 1 является корнем уравнения.
Разделим многочлен х 2 + 2х – 3 на двучлен х – 1:
_ х 2 + 2х – 3 х – 1
Уравнение принимает вид: (х – 1)( х +3) = 0
Левая часть уравнения обращается в нуль при х = -3,
а также при х = 1, это означает, что числа -3 и 1
являются корнями данного уравнения.
9. Графический способ
Если в уравнении x 2 + px + q = 0 перенести второй и третий члены в правую часть, то получим x 2 = – px – q.
Построим графики зависимостей у = х 2 и у = – px – q .
1. Если прямая и парабола пересекаются в двух точках – 2 решения;
2. Если прямая и парабола касаются — 1решение;
3. Если прямая и парабола не имеют общих точек – корней нет.
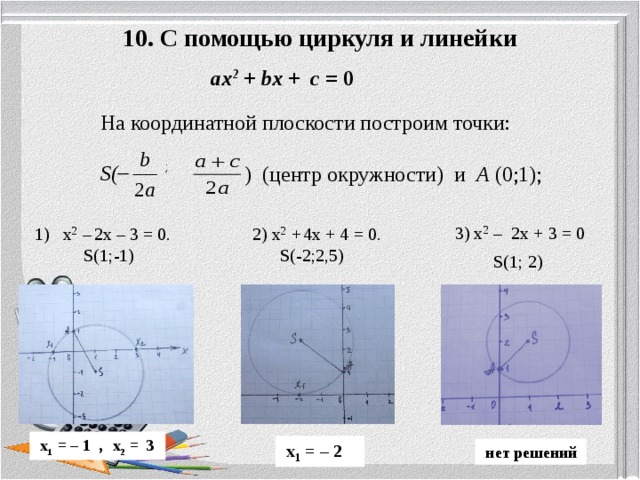
10. С помощью циркуля и линейки
На координатной плоскости построим точки:
) (центр окружности) и А (0;1);
3) х 2 – 2х + 3 = 0
1) х 2 – 2х – 3 = 0.
2) х 2 + 4х + 4 = 0.
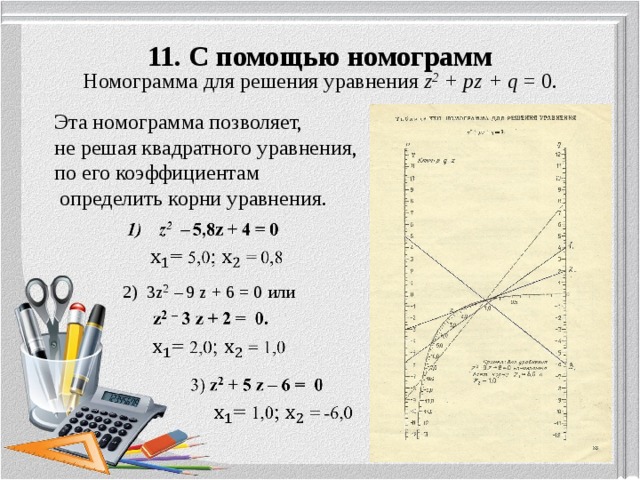
11. С помощью номограмм
Номограмма для решения уравнения z 2 + pz + q = 0.
Эта номограмма позволяет,
не решая квадратного уравнения,
по его коэффициентам
определить корни уравнения.
2) 3z 2 – 9 z + 6 = 0 или
12. Геометрический способ
Решим геометрически уравнения х 2 + 2х – 3 = 0.
Преобразуя уравнение, получаем х 2 + 2х = 3.
На рисунке находим «изображения» выражения х 2 + 2х,
т.е. к площади квадрата со стороной х два раза прибавляем
площади прямоугольников со сторонами, равными 1 и х.
К выражению х 2 + 2х добавился квадрат площадью 1.
х 2 + 2х + 1 = 3 + 1.
х + 1 = 2 и х + 1 = -2,
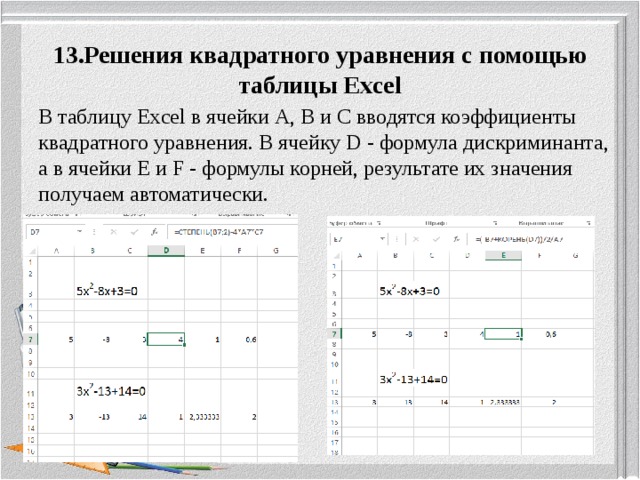
13.Решения квадратного уравнения с помощью таблицы Excel
В таблицу Excel в ячейки А, В и С вводятся коэффициенты квадратного уравнения. В ячейку D — формула дискриминанта, а в ячейки Е и F — формулы корней, результате их значения получаем автоматически.
Сравнение разных способов решения квадратных уравнений
1. Разложение левой части уравнения на множители
Можно решить, не зная формул
2. Метод выделения полного квадрата
Подходит не ко всем уравнениям
быстрее находятся корни
3. Формула корней квадратного уравнения
4. С использованием теоремы Виета
Для всех квадратных уравнений
Быстрота решения, экономия времени
5. Способ «переброски»
Дробные коэффициенты уравнения
Быстрота решения, если корни целые
6. Свойство делителя свободного члена
Дробные коэффициенты уравнения
Быстрота решения и экономия времени
7. Свойства коэффициентов
8. Следствие теоремы Безу
Подходит не ко всем уравнениям, дробные коэффициенты уравнения
Подходит только для некоторых уравнений
9. Графический способ
Подходит не ко всем уравнениям.
10. С помощью циркуля и линейки
11. С помощью номограммы
12. Геометрический способ
13. С помощью таблицы Excel
Подходит не ко всем уравнениям.
Умение решать квадратные уравнения разными способами позволяет:
- экономить время, применяя быстрый способ решения;
- решать уравнения с большими коэффициентами;
- выполнять автоматические расчёты;
- наглядно представлять решение уравнения;
- решить любое квадратное уравнение по формуле. .
«Быстрые способы решения квадратных уравнений»
- Глейзер Г. И. История математики в школе. – М.: просвещение, 1982 Брадис В. М. Четырехзначные математические таблицы для среденй школы. – м., просвещение, 1990 Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение, 2015 М., Математика (приложение к газете «Первое сентября»), №№ 21/96, 10/97, 24/97, 40/2000. Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. М., Квант, №4/72. С.34.
- Глейзер Г. И. История математики в школе. – М.: просвещение, 1982
- Брадис В. М. Четырехзначные математические таблицы для среденй школы. – м., просвещение, 1990
- Макарычев Ю.Н., Миндюк Н.Г. Алгебра. Учебник для 8 класса. М., Просвещение, 2015
- М., Математика (приложение к газете «Первое сентября»), №№ 21/96, 10/97, 24/97, 40/2000.
- Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. М., Квант, №4/72. С.34.
6.Стратилатов П.В. «Повышение вычислительной культуры учащихся средней
- 6.Стратилатов П.В. «Повышение вычислительной культуры учащихся средней
школы». М., «Просвещение», 1965.
7. Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005.
8. Энциклопедический словарь юного математика. – М.: Педагогика, 1985.
- школы». М., «Просвещение», 1965. 7. Штейнгауз В.Г. Математический калейдоскоп. – М.: Бюро «Квантум», 2005. 8. Энциклопедический словарь юного математика. – М.: Педагогика, 1985. 9. https://ru.wikipedia.org/wiki 10. http://science-start.ru/ru/article/view?id=15
Источник