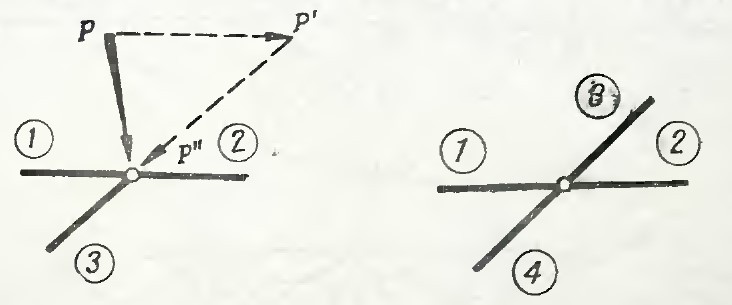Решение фермы графическим способом

Основы расчёта ферм: ручной и машинный счёт

Фермами называют плоские и пространственные стержневые конструкции с шарнирными соединениями элементов, загружаемые исключительно в узлах. Шарнир допускает вращение, поэтому считается, что стержни под нагрузкой работают только на центральное растяжение-сжатие. Фермы позволяют значительно сэкономить материал при перекрытии больших пролётов.

• по очертанию внешнего контура;
• по виду решётки;
• по способу опирания;
• по назначению;
• по уровню проезда транспорта.

Также выделяют простейшие и сложные фермы. Простейшими называют фермы, образованные последовательным присоединением шарнирного треугольника. Такие конструкции отличаются геометрической неизменяемостью, статической определимостью. Фермы со сложной структурой, как правило, статически неопределимы.

Для успешного расчёта необходимо знать виды связей и уметь определять реакции опор. Эти задачи подробно рассматриваются в курсе теоретической механики. Разницу между нагрузкой и внутренним усилием, а также первичные навыки определения последних дают в курсе сопротивления материалов.

Рассмотрим основные методы расчёта статически определимых плоских ферм.

Способ проекций

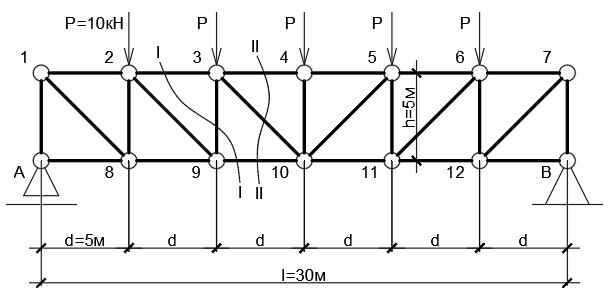
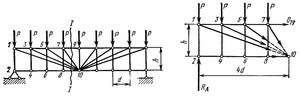
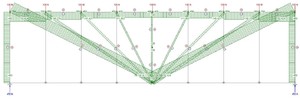
На рис. 2 симметричная шарнирно-опёртая раскосная ферма пролётом L = 30 м, состоящая из шести панелей 5 на 5 метров. К верхнему поясу приложены единичные нагрузки P = 10 кН. Определим продольные усилия в стержнях фермы. Собственным весом элементов пренебрегаем.

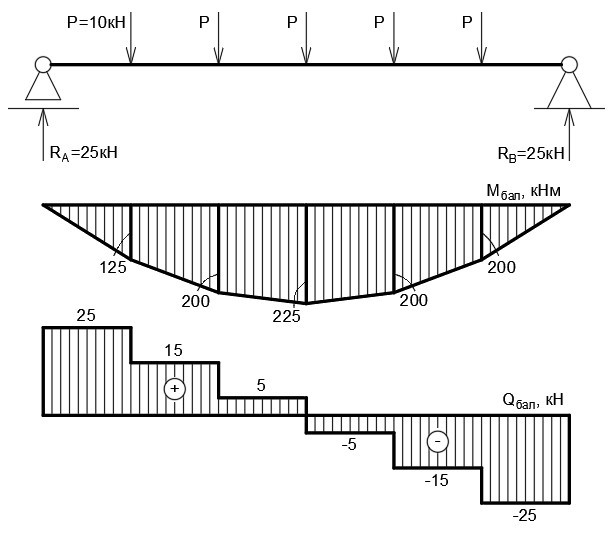
Опорные реакции определяются путём приведения фермы к балке на двух шарнирных опорах. Величина реакций составит R (A) = R (B) = ∑P/2 = 25 кН. Строим балочную эпюру моментов, а на её основе — балочную эпюру поперечных усилий (она понадобится для проверки). За положительное направление принимаем то, что будет закручивать среднюю линию балки по часовой стрелке.

Метод вырезания узла

Метод вырезания узла заключается в отсечении отдельно взятого узла конструкции с обязательной заменой разрезаемых стержней внутренними усилиями с последующим составлением уравнений равновесия. Суммы проекций сил на оси координат должны равняться нулю. Прикладываемые усилия изначально предполагаются растягивающими, то есть направленными от узла. Истинное направление внутренних усилий определится в ходе расчёта и обозначится его знаком.

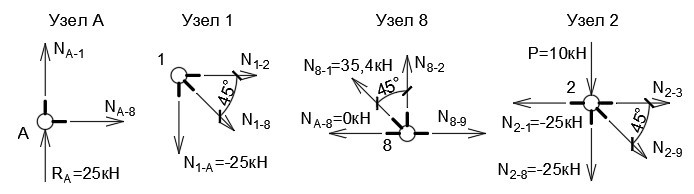
Рационально начинать с узла, в котором сходится не более двух стержней. Составим уравнения равновесия для опоры, А (рис. 4).

Очевидно, что N (A-1) = -25кН. Знак «минус» означает сжатие, усилие направлено в узел (мы отразим это на финальной эпюре).

Условие равновесия для узла 1:

Из первого выражения получаем N (1−8) = —N (A-1)/cos45° = 25кН/0,707 = 35,4 кН. Значение положительное, раскос испытывает растяжение. N (1−2) = -25 кН, верхний пояс сжимается. По этому принципу можно рассчитать всю конструкцию (рис. 4).

Метод сечений

Ферму мысленно разделяют сечением, проходящим как минимум по трём стержням, два из которых параллельны друг другу. Затем рассматривают равновесие одной из частей конструкции. Сечение подбирают таким образом, чтобы сумма проекций сил содержала одну неизвестную величину.

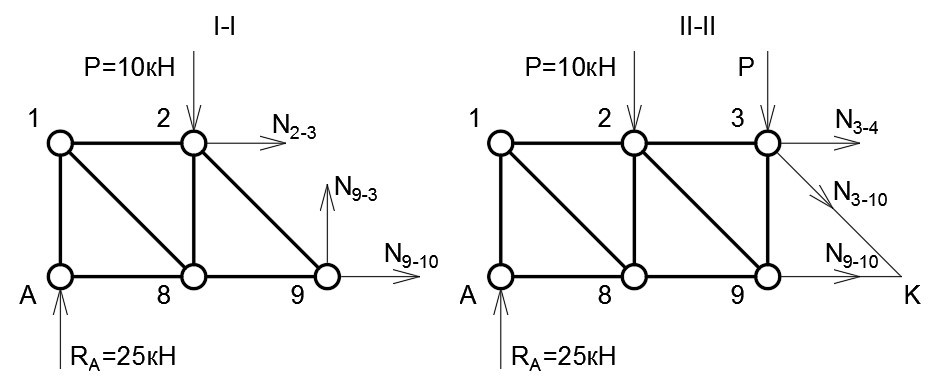
Проведём сечение I-I (рис. 5) и отбросим правую часть. Заменим стержни растягивающими усилиями. Просуммируем силы по осям:

N(9−3) = P — R(A) = 10 кН — 25 кН = -15 кН

Стойка 9−3 сжимается.

Способ проекций удобно применять в расчётах ферм с параллельными поясами, загруженными вертикальной нагрузкой. В этом случае не придётся вычислять углы наклона усилий к ортогональным осям координат. Последовательно вырезая узлы и проводя сечения, мы получим значения усилий во всех частях конструкции. Недостатком способа проекций является то, что ошибочный результат на ранних этапах расчёта повлечёт за собой ошибки во всех дальнейших вычислениях.

Способ моментной точки

Способ моментной точки требует составлять уравнение моментов относительно точки пересечения двух неизвестных сил. Как и в методе сечений, три стержня (один из которых не пересекается с остальными) разрезаются и заменяются растягивающими усилиями.

Рассмотрим сечение II-II (рис. 5). Стержни 3−4 и 3−10 пересекаются в узле 3, стержни 3−10 и 9−10 пересекаются в узле 10 (точка K). Составим уравнения моментов. Суммы моментов относительно точек пересечения будут равняться нулю. Положительным принимаем момент, вращающий конструкцию по часовой стрелке.

Из уравнений выражаем неизвестные:

N(9−10) = (2d∙R(A) — d∙P)/h = (2∙5м∙25кН — 5м∙10кН)/5м = 40 кН (растяжение)

N(3−4) = (-3d∙R(A) + 2d∙P + d∙P)/h = (-3∙5м∙25кН + 2∙5м∙10кН + 5м∙10кН)/5м = -45 кН (сжатие)

Способ моментной точки позволяет определить внутренние усилия независимо друг от друга, поэтому влияние одного ошибочного результата на качество последующих вычислений исключено. Данным способом можно воспользоваться в расчёте некоторых сложных статически определимых ферм (рис. 6).

Требуется определить усилие в верхнем поясе 7−9. Известны размеры d и h, нагрузка P. Реакции опор R(A) = R(B) = 4,5P. Проведём сечение I-I и просуммируем моменты относительно точки 10. Усилия от раскосов и нижнего пояса не попадут в уравнение равновесия, так как сходятся в точке 10. Так мы избавляемся от пяти из шести неизвестных:

Аналогично можно рассчитать остальные стержни верхнего пояса.

Признаки нулевого стержня

Нулевым называют стержень, в котором усилие равно нулю. Выделяют ряд частных случаев, в которых гарантированно встречается нулевой стержень.

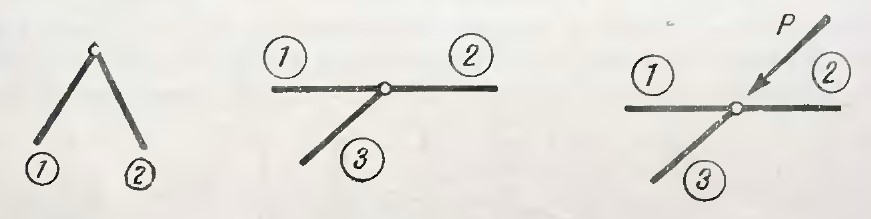
• Равновесие ненагруженного узла, состоящего из двух стержней, возможно только в том случае, если оба стержня нулевые.
• В ненагруженном узле из трёх стержней одиночный (не лежащий на одной прямой с остальными двумя) стержень будет нулевым.

• В трехстержневом узле без нагрузки усилие в одиночном стержне будет равно по модулю и обратно по направлению приложенной нагрузке. При этом усилия в стержнях, лежащих на одной прямой, будут равны друг другу, и определятся расчётом N(3) = -P, N(1) = N(2).
• Трехстержневой узел с одиночным стержнем и нагрузкой, приложенной в произвольном направлении. Нагрузка P раскладывается на составляющие P’ и P» по правилу треугольника параллельно осям элементов. Тогда N(1) = N(2) + P’, N(3) = -P».

• В ненагруженном узле из четырёх стержней, оси которых направлены по двум прямым, усилия будут попарно равны N(1) = N(2), N(3) = N(4).

Пользуясь методом вырезания узлов и зная правила нулевого стержня, можно проводить проверку расчётов, проведённых другими методами.

Расчёт ферм на персональном компьютере

Современные вычислительные комплексы основаны на методе конечного элемента. С их помощью осуществляют расчёты ферм любого очертания и геометрической сложности. Профессиональные программные пакеты Stark ES, SCAD Office, ПК Лира обладают широким функционалом и, к сожалению, высокой стоимостью, а также требуют глубокого понимания теории упругости и строительной механики. Для учебных целей и подойдут бесплатные аналоги, например Полюс 2.1.1.

В Полюсе можно рассчитывать плоские статически определимые и неопределимые стержневые конструкции (балки, фермы, рамы) на силовое воздействие, определять перемещения и температурное воздействие. Перед нами эпюра продольных усилий для фермы, изображённой на рис. 2. Ординаты графика совпадают с полученными вручную результатами.

Порядок работы в программе Полюс

• На панели инструментов (слева) выбираем элемент «опора». Размещаем помещаем элементы на свободное поле кликом левой кнопки мыши. Чтобы указать точные координаты опор, переходим в режим редактирования, нажав на значок курсора на панели инструментов.
• Двойной клик по опоре. Во всплывающем окне «свойства узла» задаём точные координаты в метрах. Положительное направление осей координат — вправо и вверх соответственно. Если узел не будет использоваться в качестве опоры, установите флажок «не связан с землёй». Здесь же можно задать приходящие в опору нагрузки в виде точечной силы или момента, а также перемещения. Правило знаков такое же. Удобно разместить крайнюю левую опору в начале координат (точка 0, 0).
• Далее размещаем узлы фермы. Выбираем элемент «свободный узел», кликаем по свободному полю, точные координаты прописываем для каждого узла в отдельности.
• На панели инструментов выбираем «стержень». Кликаем на начальном узле, отпускаем кнопку мышки. Затем кликаем на конечном узле. По умолчанию стержень имеет шарниры на двух концах и единичную жёсткость. Переходим в режим редактирования, двойным кликом по стержню открываем всплывающее окно, при необходимости изменяем граничные условия стержня (жёсткая связь, шарнир, подвижный шарнир для опорного конца) и его характеристики.
• Для загружения ферм используем инструмент «сила», нагрузка прикладывается в узлах. Для сил, прикладываемых не строго вертикально или горизонтально, устанавливаем параметр «под углом», после чего вводим угол наклона к горизонтали. Альтернативно можно сразу ввести значение проекций силы на ортогональные оси.
• Программа считает результат автоматически. На панели задач (вверху) можно переключать режимы отображения внутренних усилий (M, Q, N), а также опорных реакций (R). Результатом будет эпюра внутренних усилий в заданной конструкции.

В качестве примера рассчитаем сложную раскосную ферму, рассмотренную в методе моментной точки (рис. 6). Примем размеры и нагрузки: d = 3м, h = 6м, P = 100Н. По выведенной ранее формуле значение усилия в верхнем поясе фермы будет равно:

O(7−9) = -8d∙P/h = -8∙3м∙100Н/6м = -400 Н (сжатие)

Эпюра продольных усилий, полученная в Полюсе:

Значения совпадают, конструкция смоделирована верно.

1. Дарков А. В., Шапошников Н. Н. — Строительная механика: учебник для строительных специализированных вузов — М.: Высшая школа, 1986.
2. Рабинович И. М. — Основы строительной механики стержневых систем — М.: 1960.

Источник

Графическая статистика и методы расчета ферм

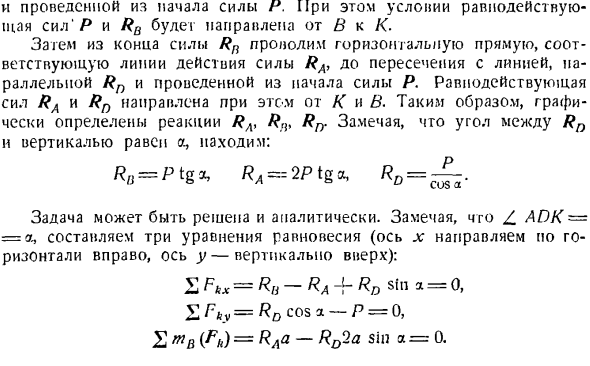
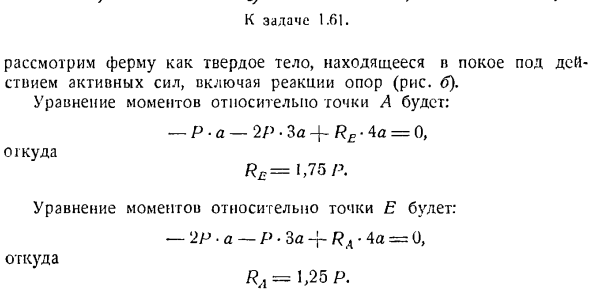
Графическая статистика и методы расчета ферм

• Графическая статистика и методы расчета фермы 1°.Равновесие системы произвольных сил. Путь последователя и отличное дополнение. Если твердое тело под действием системы любой плоской силы также находится в равновесии, то такие силы можно определить из состояния равновесия путем последовательного сложения графически неизвестных values.

In кроме того, в системе сил, приложенных к 1 твердому телу, число неизвестных не должно превышать 3.В противном случае задача не определяется статически. По сравнению с аналитическим методом решения задачи равновесия системы плоских сил этот графический метод более очевиден, но его применение при большом количестве сил очень трудоемко.

Этот графический метод решения задачи рекомендуется применять, если общее число сил, действующих на твердое тело, невелико. Людмила Фирмаль

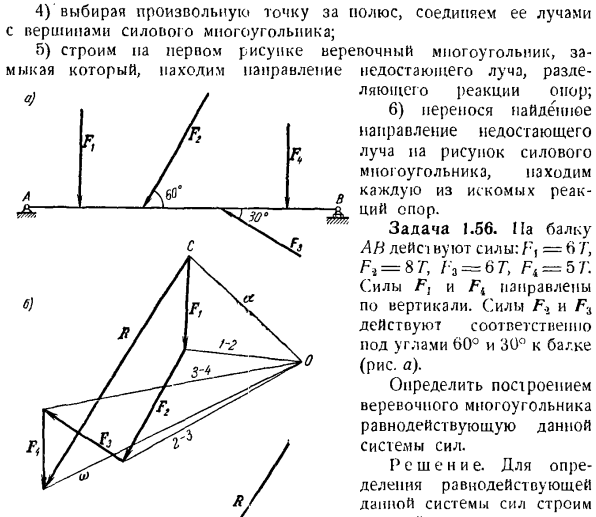
Метод добавления силы в ряд может быть применен к 2 версиям. Если под действием плоской системы заданной силы и 3 реакций твердое тело находится в равновесии, а его линии действия известны(/ j, / о,/ 3), то рекомендуется такая серия действий (1-й вариант): все известные силы получаются последовательно графически, и результат получается. 4) выделите любую точку полюсом и соедините ее с Лучом вершиной силового многоугольника. 5) на первом рисунке создайте веревочный многоугольник и закройте его.

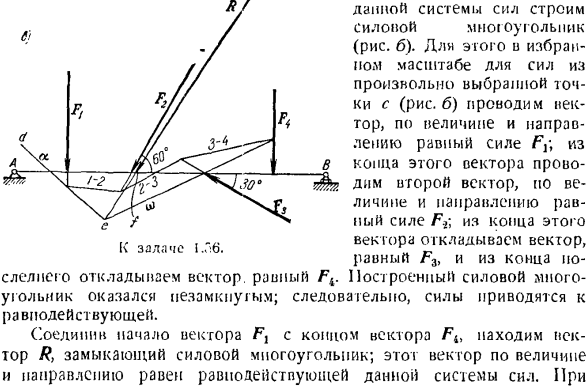
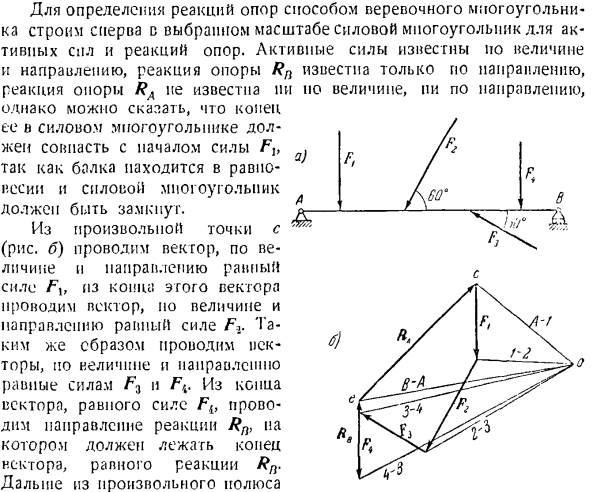
Используйте это, чтобы найти направление недостающего луча и разделить его. Опора стержня, вызывающего реакцию; 6) Если вы перенесете направление найденного недостающего луча на форму силового многоугольника, то соответственно найдете нужную реакцию опоры. Задача 1.56. Луч ПА в ЛЕ с! Сила недействительна: F,= 6’/’, F%= ST,/ * s = 67, F4 = 5T. силы F и F <направлены вертикально. Сила F и Fs действуют под углом 00°и 30° с

• Соответственно по отношению к балке (рисунок а). Создайте веревочные полигоны, чтобы определить исход этой системы сил. R s и я e. To определите последствия действия этой системы сил、 Постройте энергетический полигон этой энергосистемы (рисунок b).Для этого и выбранного масштаба силы из любой выбранной точки c (рисунок B) нарисуйте Тор, величина и направление которого равны силе F из кучи этого вектора.

Создайте канатный полигон, чтобы найти полученный объект point. Людмила Фирмаль

To сделайте это, нарисуйте Луч из произвольно выбранной точки O (рисунок B). в начале вектора Fh лучи 1-2 находятся в начале вектора Fb, лучи 2-3 находятся в начале вектора F2, лучи 3-4 находятся в начале вектора FK. Мы рисуем луч ω в конце вектора ФК.

Из любой точки d вблизи силы Fx (рисунок C) проведите прямую линию, параллельную Лучу a, проведите прямую линию, параллельную Лучу 7-2 от точки пересечения силы Fv, а из точки пересечения луча силы Z7 проведите линию, параллельную лучу силы F3 до точки пересечения нарисуйте прямую линию, параллельную лучам солнца.

Проведите прямую линию параллельную Лучу от точки пересечения луча 3-4 и линии действия силы Fi Продолжите линию, параллельную Лучу a, и проведите линию через точку e, параллельную вектору R, пока она не пересечется в точке e. точка пересечения между этой линией и Лучом выражается как a/.Это точка приложения Объединенных сил, приданных балке AB.

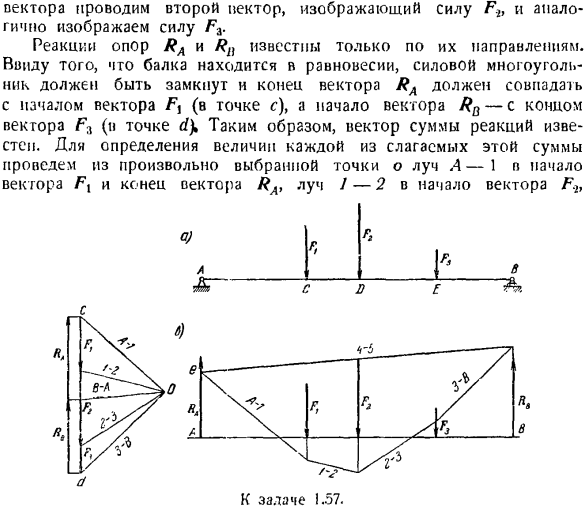
Используя выбранный масштаб путем измерения длины вектора R, найдите размер результата. 17.4 эквивалент к т. масштаб 1мм до 1/3 Т принят. Задача 1.57.Балка АВ длиной 12 м (рис. а) закреплена шариковым Кнупом с концом а, а конец В находится на опоре, прикрепленной к ролику. На балку были приложены следующие силы: Fi = 2 7, F. 2 = 3 7″, F $ = \T. расстояние: AC = 4 My CD = 2 Mt DE = 3m.

Создать веревочный многоугольник для определения реакции опоры A и B. Решение. Рассмотрим равновесие балки АВ. Активная сила действует на балку: Fu Fb F9.Применяя закон освобождения или связи, мысленно отбросьте опоры А и В и замените их действия реакциями. Реакция опоры B, которая прикреплена к ролику, направлена перпендикулярно плоскости, в которой расположен ролик, то есть вертикально вверх.

Вообще говоря, направление реакции шарнира а неизвестно, но ясно, что реакция шарнира а должна быть перпендикулярной, так как все силы, действующие на балку, направлены вертикально. Если эта реакция не вертикальная, то ее горизонтальная составляющая никак не сбалансирована, и равновесие луча невозможно.

Из вектора сила F. нарисуйте 2-й вектор, представляющий lt, и аналогично представьте силу Fz. Реакция поддержки RA и Rn известна только в ее направлении. Поскольку пучок находится в равновесии, необходимо замкнуть силовой многоугольник и сопоставить конечную точку вектора RA с начальной точкой вектора fi (точка c) и начальную точку вектора RD с конечной точкой вектора f3 (точка tf).

Известно reaction. To определите значение каждого из членов этой суммы, от произвольно выбранной точки Луча A-1 до начала вектора Fj и до конца вектора RA, от Луча 1-2 до вектора F. проведите его до начала. л. о.） Так… Д. И Е. Один. И д. К выпуску 1.57. е. \ От Луча 2-3 до начала вектора F3) от Луча 3-B до начала вектора RB(совпадает с концом вектора в точке d).Направление пучка B — / 1 неизвестно, поскольку неизвестны размеры реакций RA и RB.

Далее приступаем к постройке канатного полигона. Для этого из точки е на линии действия реакции RA (рисунок C) проведите прямую линию, параллельную Лучу A -/, из точки пересечения к точке пересечения с действием силы Fu, к точке пересечения с Лучом/-2, проведите прямую линию, параллельную лучу действия/ 7.; Аналогично проведите прямую линию, параллельную Лучу 2-3u 3-B, пока он не пересечется с рабочими линиями силы F3 и реактивной силы RB.

Поскольку система сил находится в состоянии равновесия, необходимо замкнуть многоугольник каната. Таким образом, линия между линиями действия реакции RA и RB должна проходить через точку e. он делит отрезок dc на отрезки, равные реакции Ra и Rb(для наглядности на рис.6 реакции RA и RB немного перемешаны слева).Если вы измерите значения реакции, найденные на принятой шкале, вы найдете эти значения: RAz = 3,\ T, RB = 2.9 7 *.

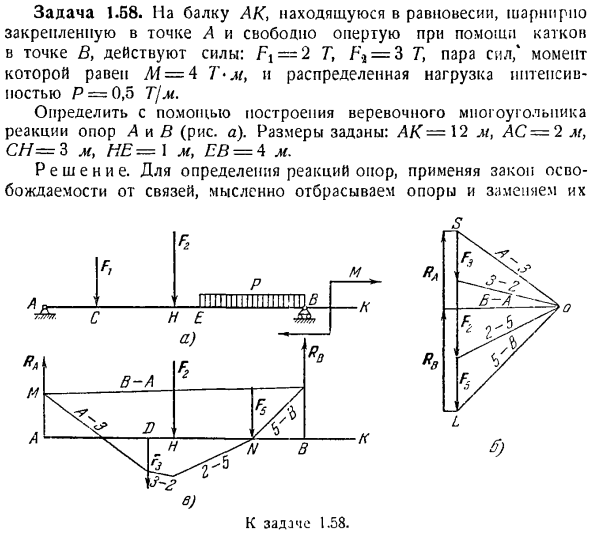
Задача 1.58.In в случае балок АК, находящихся в равновесии, закрепленных в точке А и свободно поддерживаемых роликом в точке Б, действует сила: F -2 T, t \ = 3 T, пара / момент силы составляет M = 4, распределение веса нагруженного нитепсиса.- Кость Р = 0,5 т / л *. Используя конструкцию канатного полигона, определите реакцию опор а и в(рисунок а).Размеры следующие: АК-12 М, АС-2 м, СИ = 3 г, Не-И Л/, и£= 4 г. The solution. To определите реакцию поддержки, примените законы, которые™освободил от связи, и мысленно отбросьте и обменяйте поддержку

К выпуску 1.58. ф Воздействие на луч осуществляется реакцией поддержки ядерного оружия и РБ(рисунок в).Поскольку все активные силы направлены вертикально вниз, а сумма проекций сил попарно для любой оси равна нулю, обе реакции направлены вертикально вверх. Действие пары сил не изменяется, поэтому она переносится в любое место на плоскости, не меняя момента пары, заменяя пару силой Fi и F, а абсолютное значение составляет 2 т, соответственно, на расстоянии 2 м. приложите к точкам

C и A равное 2 т и приложите к точке это уравновешенно и не будет рассматриваться в дальнейшем. Для решения задачи с использованием канатного полигона необходимо заменить распределенную нагрузку концентрацией F. модуль этой мощности Fs = P * EB = 0.5 * 4 = 2 G, приложенный к средней точке L / сегмента EB. Приступайте к построению сил polygons. To сделайте это, отложив вектор на выбранном масштабе от любой точки 6 «(рисунок Б), но модуль и направление будут равны

силе F3. ФЗ. Поскольку пучок находится в равновесии, силовой полигон должен быть замкнут, поэтому начало вектора, соответствующего реакции Rf <), должно совпадать с концом вектора, соответствующего силе Fr, и началом вектора, соответствующего силе реакции: RA>точка I-это точка I. Для наглядности нарисуйте Rls и RA (рисунок b) немного левее. Затем нарисуйте луч A-3 из любой точки o в начало вектора F3 и Луч 3-2 в начало вектора Fb 2 — Рэй 3-4 1 к началу вектора, Луча, 4-Б в начало ве

ктора R/?Луч B-A не может быть нарисован в начале вектора RA, потому что размер реакции Rn неизвестен. Чтобы определить величину реакции Rl>, приступаем к построению каната Polygon. To для этого проведите прямую линию, параллельную Лучу A-I через точку A (рисунок 0) (так как это единственная известная точка на линии действия реакции RA), пока она не пересечет линию действия силы Z7.Через эту точку пересечения проведите прямую линию, параллельную Лучу/-2, пока она не пересечет линию действия силы/ \ 2.Через эту точку пересечения пр

оведите прямую линию, параллельную лучам 2-3, пока они не пересекут линию действия силы F2.Аналогично проведите прямые линии, параллельные лучам 3-4 и 4-Б, пока они не пересекутся с линиями действия сил F4 и Ru. Прямая линия, параллельная лучу 4-B, является точкой (I. В связи с тем, что канатный полигон должен быть закрыт, когда система находится в равновесии, точка d соединяется с точкой A, где начинается

построение канатного полигона. Теперь можно провести луч B-A через полюс o параллельно прямой dA (рисунок B).Лучи B-A пересекают направление реакции Rn в точке e, определяющей конечную точку вектора RB. Если соединить конец вектора RB с началом вектора Ft, то можно найти размер и направление реакции RA. By измерение сегментов, которые нарисовали реакцию

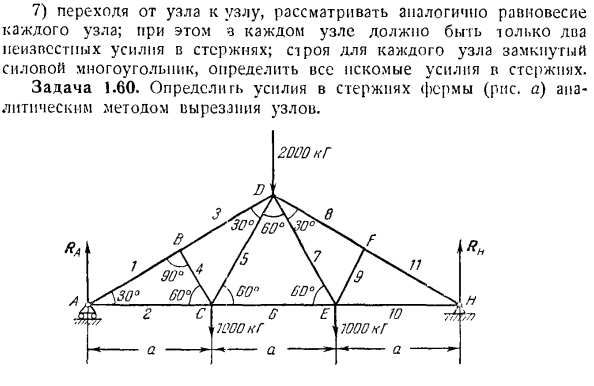
И. Я. И. м — ’2Н-3. Количество стержней: то есть, если вы удовлетворяете этому уравнению, можно рассмотреть 2 случая. 2/7 −3.、 В этом случае ферма статически неопределима. Т СЖ. С AL * b Ву-г-г К задаче 1.60. The solution. To определив силу тяги, необходимо сначала найти с

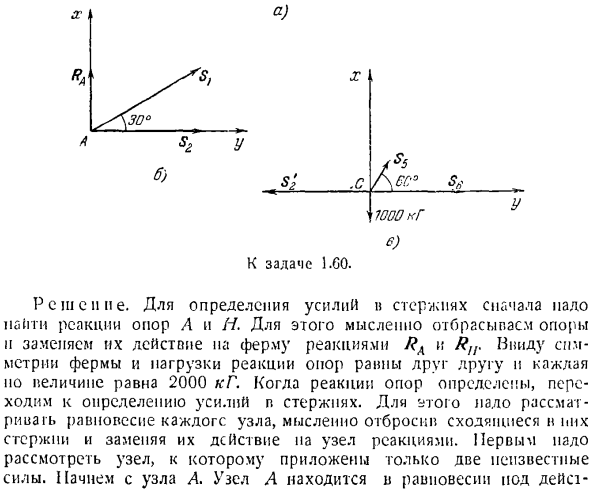
илы реакции опоры А и Н. для этого мысленно выберите опору опоры, а действие в трузиону? Когда противодействие опоры определено, приступают к определению силы в стержне. По этой причине мы рассматривали равновесие каждого узла, мысленно отбрасывая сходящиеся на них стержни и заменяя действие на узле реакцией. Первое, что нужно рассмотреть, — это узел, в котором применяются только 2 неизвестные силы. Начнем с узла А. узел а、 е.） Известными реакциями РА и неизвестных реакций стержней Г и 2.Обозначим реакцию стержней (соответственно, на рисунке Б) и выведем их из узлов. Поэтому будем считать, чт

о стержень растянут. Затем проведите ось l *через точку A и составьте систему уравнений равновесия узла A. сумма проекций всех сил на эти оси равна нулю. Проекционные уравнения для осей jc и y выглядят следующим образом: + cos 30°= 0, Ra + Sx cos 60°= 0 Я найду тебя отсюда.： = −4000 кг,= 3404 кг. Отрицательное значение реакции S1 фактически направлено в противоположную сторону, и стержень Y не растягивается, как ожидалось, что указывает на то, что еж r растянут. Теперь вернемся к изучению равновесия узлов B. In узел B, 3 стержня сходятся, из кото

рых 3 стержня / и 3 соединены вдоль 1 Прямой линии, а 4 стержня наклонены против them. No активная сила приложена к узлу B. As в результате эструс В находится в равновесии с йодом за счет действия 3 стержневых реакций. Э / о возможен только в том случае, если сила тяги 4 равна силе пули. Это объясняется тем, что он проецируется только в направлении, перпендикулярном стержню 4.

Возврат в узел С. узел С находится в равновесии под действием 2 неизвестных реакций, причем известная реакция S’ir равна по величине активной силе Sc, G до 1000, а реакция S, приложенная к узлу а, направлена в противоположную сторону(рис. с).Нарисуйте координатные оси через точку C и добавьте уравнения равновесия узла C. уравнения проекции на оси jc и y выглядят следующим образом: — SH — ^ cos 60° — pbe = 0, Si cos 30°-1000 = 0 Я найду тебя отсюда.： = 1155 кгр ^ = 2886,5 кг.

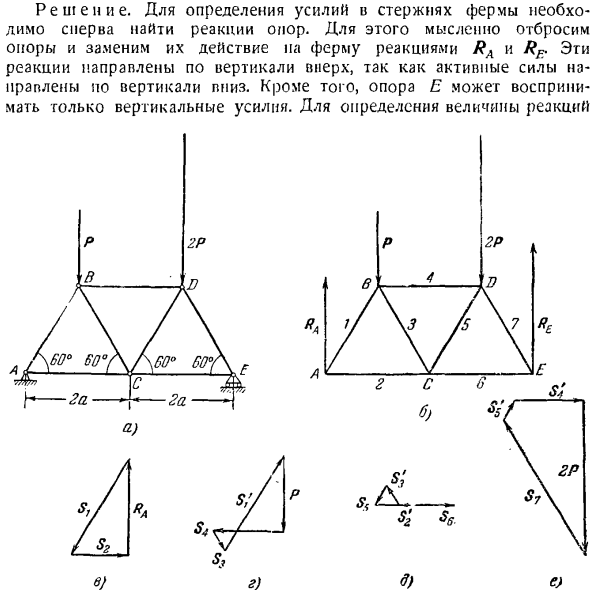
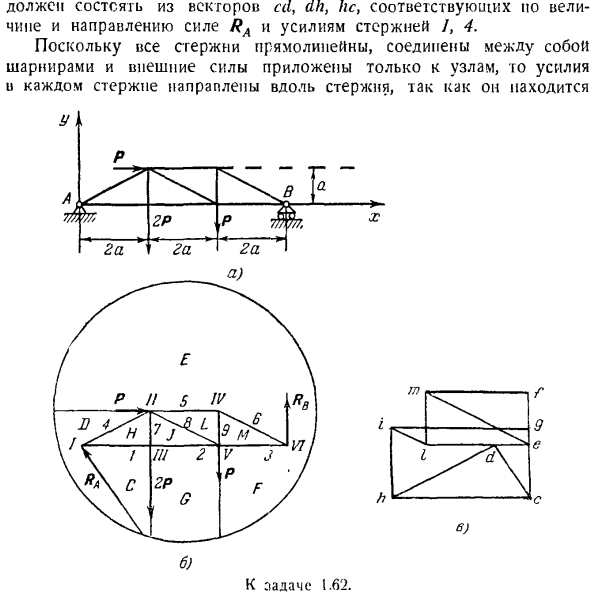
В результате стержни 5 и 6 находятся в заточении, как и ожидалось. Полная симметрия (достаточно определить мощность стержня в левой половине фермы с точки зрения вяза и / или применяемого в узлах оборудования); например, силы стержней 1 и Y, 2 и 10 равны по симметрии. Задача 1.61.Вырежьте узлы и графически определите работу пермской фермы (рисунок а) на ферме. E с PE в neck. To определить реакцию в точках A, B, D, рассмотреть равновесие стержня CD. На стержень па действует 1 активная сила-сила тяжести Р, направленная вдоль стержня.

Стержень находится в равновесии под действием 4 сил: веса P, реакции наклонной плоскости и цилиндрических соединений A и B. используя закон освобождения от связи, мысленно отбросьте связь и замените действие на стержень реакцией(рисунок B). Реакция гладкой наклонной плоскости R приложена в точке D и направлена перпендикулярно наклонной плоскости. Поскольку такой шарнир не препятствует движению вдоль оси, противодействие цилиндрического шарнира направлено

перпендикулярно оси шарнира. Эти реакции называются RA и RB (рисунок B).Таким образом, стержень CD находится в равновесии как свободное твердое тело с 4 действующими силами: P, RA, Rfi, Rfy Продлите линии действия реакций RA и Rn до тех пор, пока они не пересекутся в точке K(рисунок B).Пройдите через линию действия 2 сил с равными эффектами! Проходя через пятно

ферму как покоящееся твердое тело под действием комбинации активных сил, включая реакцию опоры (рисунок б).Уравнение момента для точки A имеет вид: -П•а-2Р * б + р£ * 4а = 0、 Откуда? Я£= 1.75 Р. Уравнение момента для точки E имеет вид: −2Р•а-Р-За+ Ра•4а=О、 Откуда? Ял = 1,25 П. После определения реакции опоры, затем найти силу стержня. Стержень обозначается цифрами 7, 2, 5, 7. Сначала вырезают узел, в котором действуют только 2 неизвестные силы, например, узел L. 3 силы прикладываются к узлу A. RA опорная реакция, s-резка по реакции, стержень 7

.Его размер неизвестен. Напомним, что если оба конца прямого стержня закреплены шарнирами, а все силы приложены только к узлам, то совпадение направления стержня и реакции наблюдается всегда. Чтобы определить величину реакции стержней, постройте треугольник сил и отложите их в сторону в том порядке, в котором они возникают при повороте узлов по часовой стрелке. Первое место в шкале занимает известное значение RA (рисунок O).Начиная с его конца, проведите прямую линию, параллельную стержням 7 и 2, пока они не пересекутся на стержнях 7 и 2

.Стороны полученного треугольника реагируют S и S. 2. определите, чтобы найти их направление, переместите вокруг треугольника силы в направлении, указанном известной силой RA. Когда узел находится в сбалансированном состоянии, стрелки замкнутого силового полигона перемещаются в одном направлении. Если переместить реакцию Si на стержень 7, то можно увидеть, что стержень 7 сжат, потому что он направлен к участку. Реакция S. Если переместить 2 на стержень 2, то можно увидеть, что это реакция из узла A. Таким образом, стержень 2 растягивается. З

атем отключите узел I. 4 прилагаются усилия.2 неизвестные реакции » стержень-3 и-4, 53 и-S4, стержень — / известные реакции. Активная сила R. вы создаете полигоны для этих сил. Сначала поместите силу Sj на шкале (рисунок D), добавьте активную силу P к ее концу, а затем проведите прямую линию, параллельную стержню 4 через конец силы P, и прямую линию, параллельную стержню 3 через начало силы S. Стороны полученного прямоугольника определяют реакцию Sz. To найдя их направление, мы движе

мся по квадрату в направлении, указанном известными силами. Если мы передадим ответ 5H на стержень 3, мы увидим, что он ориентирован от узла B, и в результате стержень 3 растягивается. Перенаправление реакции Sk от стержня 4 направляется к узлу B, поэтому стержень 4 сжимается. Затем разрезают узел C. 4 прилагаются усилия.2 неизвестные реакции и 56 стержней 5 и B, и 2 известные реакционные стержни 2 и 3, равные реакциям 53 и Sb

Пока они не пересеклись. Если мы переместим многоугольник полученной силы в направлении, указанном известными силами, мы увидим направление реакции S и S. Если вы переместите реакцию 53 на стержень 3 и реакция стержня S8) находится в равновесном состоянии при SJ0.To найдите размер этих реакций, создайте уравнения равновесия на левой стороне фермы. Это сделает сумму моментов всех сил равной нулю по отношению к точкам/и L, где пересекаются линии действия 2 неизвестных и неизвестных сил. По этой причине уравнение момента содержит только 1 неизвестный. Следовательно, уравнение момента для точки / равно: Ра. 2а-Р•2А-2

Р•а-F СГ•а = О.、 Откуда? $ п= — № Отрицательное значение величины реакции, по сути, указывает на то, что стержень 8 сжат, так как эта реакция направлена в направлении, противоположном принятому, то есть к узлу E. уравнение момента для точки L имеет вид: −2Р-а-2Р-2а-Р-За•Ф — РА•3а-Sl0•а=О、 Откуда? = ОПЕРАЦИЯ. Как и ожидалось, ядро JO было расширено. Так как силы SH и S, rt параллельны, то на их пересечении отсутствует эструс. Таким образом, вместо уравнения момента мы строим уравнение проекции для всех сил на вертикальную ось, перпендикулярную стержням 8 и JO-для определения силы. РА-Р-2л-2П

в COS 45°= О、 Откуда? Отрицательное значение реакции серы, по сути, направление, противоположное направлению, в котором используется реакция, т. е. направлено к узловой точке l, указывая на то, что стержень ９が圧 圧縮されること 。す。Аналогично, сила может быть определена методом поперечного сечения стержня этой фермы. Чтобы овладеть навыками решения задач, необходимо знать, как решать задачи с помощью И. В. Мещерского из сборника задач теоретической механики издания с 1950 года рекомендует решать следующие задачи：199、202、204、205、206、207 。 При этом условии равнодействующая сил Р и RB направлены от B до K. Затем от конца силы Rn проведите го

ризонтальную линию, соответствующую линии действия силы Ra, пересекая линию, параллельную силе R, и от начала силы P до чертежа. Результирующие мощности Ra и Rn направлены от K и B. l, Rn. Заметив, что угол между Rn и вертикальной линией равен a, мы видим, что: Р, = р ТГО, Ра-ИС ТГА, РД =〜 Задача может быть решена аналитически. Заметим, что Z AIC = = a, составляют 3 уравнения равновесий(ось l; горизонтально вправо, ось y-вертикально вверх）： 2Fk * = ра-ра + РД грех = о、 В Fby = РД, потому что а-Х = 0,£ТВ(FН)= Раа-RD2a грех = 0 Для овладения на

выками решения задач с равновесием в организме методом непрерывного сложения сил рекомендуется графически решать следующие задачи из «сборника теорий». Механиксвилл. В. М Е- 1ч / Терский, издание sJoj 1950 и др. 2°.Применение канатного полигонального метода для силовых плоских систем. Использование метода канатных полигонов для сложения

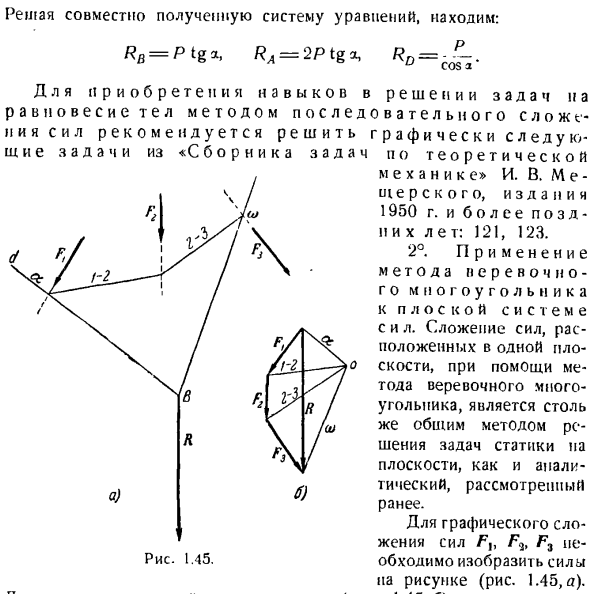
сил, расположенных в одной плоскости, является распространенным способом решения статических задач на плоскости, как и в случае ранее рассмотренных аналитических задач. Сила F. Для добавления J графики, F3 составляет 1.45.Кинематографические способности Рисунок (рисунок 1.45, a). Если решить систему уравнений, полученных совместно, то получим RB = P tgo, Ra =2Ptg a,=.

Далее построим силовой полигон (рис. 1.45.6), и первая сила Fl, за исключением любой точки? Вы также можете использовать его головы отсвоего вектора FT и ее главный вектор КТ от вектора Ф3.Начало Первой силы связано конем и вектором I последней силы. Вектор R определяет величину и направление результата. Чтобы найти линию действия, возникающую из нее, Выберите любую точку O позади полюса и соедините начал

о и конец каждой силы с прямой линией, называемой полюсом и Лучом. Первый луч обозначается а, а Луч обозначается w от конца первой силы до начала Второй, до последнего луча, например, 1-2. Далее (Рис.1.45, а) проведите прямую линию от любой точки d, параллельной Лучу i, до пересечен

ия с линией действия силы Flt; от этой точки проведите прямую линию, параллельную Лучу 1-2, до пересечения силы Ft с линией действия; от этой точки проведите прямую линию. Прежде чем пересечь линию действия последней силы Fv, проведите прямую линию, параллельную Лучу 2-6 от этой точки, параллельную Лучу w. затем продолжайте полученные лучи a и w до пересечения в точке B, что составляет 1 точку на линии действия результата. Перемещая найденный вектор из многоугольни

ка сил в точку B, можно считать задачу нахождения результирующей системы сил решаемой-Flt Fit F3. 1. 45 построенная поверх рисунка пунктирная линия называется канатным многоугольником. Это решение может быть применено к любому количеству сил в одной плоскости. Если система сил находится в равновесии, то силовые полигоны и канатные полигоны должны быть closed. So, рис. 1.45, конец последней силы должен сов

падать с началом Первой силы. Рис. 1.45, а лучи a и w должны быть направлены по прямой линии. Если силовой полигон замкнут, а канатный полигон не замкнут, то силовая система сводится к паре forces. In в этом случае в силовом полигоне лучи a и w сливаются в 1 прямую линию, а в канатном полигоне лучи a и w параллельны друг другу. Для решения задачи определения составной плоской системы сил методом канатного полигона рекомендуется следующая последовательность действий: 1) Нарисуйте твердое тело с приложенной силой, в выбранно

м масштабе рисунка. 2) Создайте силовые полигоны по отдельности и найдите их замыкание R\ 3) выделите любую точку полюсами и соедините ее с вершиной силового многоугольника прямой линией-лучами, обозначенными а, 1-2, 2-3. 4) Создайте первую фигуру. Это показывает твердый, веревочный многоугольник с prg-силой. 5) веревкой переходим к пересечению лучей a и w многоугольника и находим точку на линии действия результата. 6) нарисуйте результат через полученную точку, параллельную основному вектору силового многоугольника. При реш

ении задачи определения реакции твердой опоры в состоянии равновесия под действием»системы плоских сил» необходимо придерживаться следующей последовательности действий: 1) Нарисуйте твердое тело с активной силой на выбранном масштабе; 2) мысленно отбросьте опору и замените опору на нужную реакцию. 3) Создайте силовой полигон, где сумма требуемых реакций определяется на отдельном рисунке.

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

© Фирмаль Людмила Анатольевна — официальный сайт преподавателя математического факультета Дальневосточного государственного физико-технического института

Источник