Решение алгоритмов табличным способом

Средства представления алгоритмов

Процесс составления алгоритмов называют алгоритмизацией. Алгоритм можно представить различными способами: с помощью графического или текстового описания, в виде таблицы значений.

Графический способ представления алгоритмов имеет ряд преимуществ благодаря визуальности процесса решения задачи. Алгоритмы, представленные графическими средствами, получили название визуальные алгоритмы или блок – схемы .

Текстовое описание алгоритма является достаточно компактным и может быть реализовано на абстрактном или реальном языке программирования в виде программы для ЭВМ. Таблицы значений представляют алгоритм неявно, как некоторое преобразование конкретных исходных данных в выходные.

Табличный способ описания алгоритмов. Применяют для проверки правильности функционирования алгоритма на конкретных тестовых наборах входных данных, которые вместе с результатами выполнения алгоритма фиксируются в «таблицах трассировки».

Все три способа представления алгоритмов являются взаимодополняющими. На этапе проектирования наилучшим является графическое представление, на этапе проверки алгоритма — табличное описание, на этапе применения — текстовая запись в виде программы.

Визуальное представление алгоритмов

При проектировании визуальных алгоритмов используют специальные графические элементы, называемые графическими блоками, которые представ-лены в таблице. Существует Государственный стандарт (ГОСТ 19.002-80 и ГОСТ 19.003-80), определяющий правила выполнения схем и обозначения для отдельных операций.

Правила проектирования визуальных алгоритмов:
• В начале алгоритма должны быть блоки ввода значений входных данных.
• После ввода значений входных данных следуют блоки обработки и блоки условия.
• В конце алгоритма должны располагаться блоки вывода значений выходных данных.
• В алгоритме должен быть только один блок начала и один блок окончания.
• Связи между блоками указываются направленными или ненаправленными линиями.
• Данные, вычислительные формулы, логические выражения располагают внутри соответствующих блоков.
• Блоки могут сопровождаться комментариями в виде выносок.

Графическое представление алгоритмов имеет практическое значение не только для программистов. Те же информационные схемы (инфографика) используются журналистами для визуализации данных. Структурные схемы последовательности монтажа полезны для сборщиков мебели, например. Та же визуализация алгоритма трассировки (алгоритм Ли) может быть полезна для конструирования печатных плат, особенно когда требуется срочное изготовление таких плат по требованиям заказчика.

Источник

3.2. Формы представления алгоритмов

Алгоритмы имеют несколько форм представления: словесную, формульно-словесную, табличную, в виде блок-схем.

Словесная форма является самой простой и доступной. Содержание последовательных предписаний — вычислений задается в произвольной краткой форме на естественном языке, не допускающем повторений, неоднозначного понимания выражений, лишних слов. Недостаток словесной формы — отсутствие более или менее строгой формализации и наглядности вычислительного процесса. Она не подходит для задач со сложной логикой и вычислительным процессом и применима для простых алгоритмов, отличающихся однократной последовательностью выполнения предписаний.

Пример: Записать алгоритм вычисления y по формуле:

1) умножить x на3;

2) к результату первого действия прибавить 1;

3) из результата второго действия извлечь корень;

4) умножить x на x;

5) из результата четвертого действия вычесть 3;

6) результат пятого действия разделить на результат третьего. Полученный результат считать значением y.

Формульно-словесный способ основан на задании предписания алгоритма с использованием математических формул и словесных пояснений. Формулы в сочетании с правилами их написания представляют собой алгоритмический язык, применимый для задания вычислительных алгоритмов. Этот способ более нагляден и компактен по сравнению со словесным. Однако формула устанавливает последовательность действий неоднозначно, т.е. не совсем полно отражаются свойства детерминированности и определенности.

задает объем усеченного конуса. Здесь h-высота, R и r — соответственно радиусы нижнего и верхнего основания.

Табличная форма записи. Существует несколько типов таблиц. Первый используется при организации вычислений по формуле с пооперационной регистрацией промежуточных результатов. Разбиение формулы на последовательность элементарных действий дает последовательность предписаний. Такая форма наиболее применима тогда, когда требуется вычислить несколько значений одного выражения для различных значений входных величин.

Пример: Для предыдущей формулы составим табличную запись алгоритма (рис. 3.1)

Рис.3.1. Табличная запись алгоритма

Второй тип таблицы называется решающей таблицей. В простейшем случае она включает 4 части: перечень условий, указатель условий, перечень действий, указатель действий (рис.3.2).

Перечень условий содержит все условия, а перечень действий — все действия, проверка и выполнение которых необходимы в процессе решения задачи. Они располагаются одно за другим; в строке записывается только одно условие или действие. Правая часть делится на несколько столбцов, в которых определяется, какие условия следует проверить, а какие действия следует выполнить в результате проверки этих условий. На пересечении соответствующих столбцов и строк ставится Y в том случае, если условие должно выполняться, N — если нет и «-«, если условие не учитывается.

Рис.3.2. Общий вид решающей таблицы

Когда условие требует выполнения некоторого действия, то на пересечении соответствующих столбцов и строк, ставится символ X. В случае отсутствия действия позиция остается незаполненной.

Если условие формируется так, что возможны два ответа, «да» — «нет» или «Y» — «N», то таблицы называются таблицами с ограниченными входами. Если ответов несколько, то таблицы называются таблицами с расширенными входами. При этом простое условие записывается так же, как и в таблицах первого вида, сложные действия распределяются между столбцами.

Пример: Алгоритм поиска HOD в виде решающей таблицы с расширенными входами показан в таблице 3.2.

Блок-схемой называется графическое изображение алгоритма, дополненное элементами словесной записи, в котором каждое предписание алгоритма представляется в виде геометрического символа, имеющего определенную конфигурацию в зависимости от характера выполняемой операций или отображаемой функций.

Для однозначного обозначения одинаковых процедур формы, размеры и правила оформления определены ГОСТ 19.003-80 «Схема алгоритмов и программ. Обозначения условные и графические» и ГОСТ 19.002-80 «Схема алгоритмов и программ. Правила оформления».

Наиболее употребительные символы приведены в табл. 3.3.

При начертании символов их размеры выбираются кратными 5, размер (а) равным 10,15,20. размер (b) составляет b=1,5a.

Выполнение действий или последовательности действий

Выбор направления выполнения алгоритма в зависимости от некоторого условия

Выполнение операций, меняющих команды или группы команд. Начало цикла

Вычисления по подпрограмме, стандартной программы

Ввод исходных данных или вывод результатов

Вывод, печать результатов на бумаге

Ввод и вывод данных, носителем которых являются перфокарты

Операция по преобразованию информации

Ввод вывод данных, носителем которых является магнитный диск

11

Ввод вывод данных, носителем которых является магнитный ленте

12

Пуск — остановка (знак завершения)

Начало, конец, алгоритма, вход и выход в подпрограмму

12

Указание последовательности связей между символами

Указание связей между прерванными линиями

14

Указание связей между элементами схемы, расположенными на разных местах

Последовательность выполнения пунктов алгоритма, описываемого блок-схемой, устанавливается путем упорядоченного размещения блоков на схеме и объединение их линиями потока. Нормальное направление линии потока — сверху вниз и слева направо. Линии проводятся строго вертикально и горизонтально и завершаются на середине символа. Если направление потока совпадает с нормальным — стрелки не ставятся, если в противоположном направлении — стрелки ставятся. В месте слияния линии потока ставится точка. В месте пересечения линии потока точка не ставится (рис.3.3).

Выходы символа «Решение» помечаются символами «да»/»нет»- т.е. выполняется или не выполняется условие. Условие записывается внутри символа (рис.3.4). Содержание надписи внутри символа или рядом должно быть кратким, без сокращений, за исключением допустимых сокращений. Записи представляются так, чтобы их можно было читать слева направо, сверху вниз.

Для удобства нахождения символа задаются их координаты в виде цифр, букв или цифр и букв. Они представляются сверху слева в разрыве контура (рис.3.5).

Блок-схема является исключительно наглядным и простым способом представления алгоритма. При этом нет никаких ограничений степени детализации в его изображении. Если блок-схема получается очень сложной и теряет свойства иллюстративности, вначале составляют укрупненную блок-схему всего вычислительного процесса, затем каждый ее блок представляется отдельной блок-схемой.

Для блок-схем обязательны следующие правила: каждый блок имеет только один вход и выполнение описанных в них действий всегда начинается с первого; входить в середину блок-схемы нельзя. Вход в блок-схему обозначается символом «начало», заканчивается блок-схема символом «конец».

Соединители в разрыве линии обозначаются общим идентификатором, в качестве которого может использоваться цифра, буква или буква и цифра (рис.3.6).

Межстраничный соединитель маркируется двумя строками символов: первая строка определяет лист, вторая является идентификатором самого соединения (рис.3.7).

В качестве примера рассмотрим блок-схему алгоритма Евклида нахождения НОД двух чисел (рис.3.8).

С 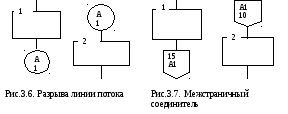уществуетоператорная схема записи алгоритма. При операторном способе записи алгоритма каждое предписание (процедура) обозначается определенным символом-оператором. Операторы записываются построчно в порядке их выполнения. В зависимости от своего назначения операторы делятся на действующие, логические и варьирующие.

Действующие осуществляют непосредственно вычислительные и другие преобразующие операции над информацией.

Логические описывают условия, от которых зависит направление решения.

Варьирующие предусматривают изменение вспомогательных величин, называемых параметрами. Обычно параметры являются либо номерами изменяемых объектов, носящих одинаковые номера (массивы), либо номерами операторов, по какой-то причине объединенных в одну группу.

Полная последовательность операторов, задающая весь процесс решения, называется схемой решения. Операторы на схеме обычно обозначаются условными (стандартными) символами. Наиболее употребительными являются следующие:

Nо — начало процесса;

В — ввод исходных данных;

D(A) — действующий (арифметический);

W — оператор печати (вывода);

E — оператор останова.

Знаки переходов имеют вид полускобок с числовыми индексами. Левыми полускобками ₃  5 указывается передача управления. Правая нижняя полускобка указывает прием управления ₃  ₅  , она может соответствовать как верхнему, так и нижнему знакам передачи управления Соответствие определяется равенством числовых индексов После логического оператора могут стоять верхняя и нижняя полускобка передачи управления. Верхняя полускобка соответствует » да «, т.е. выполнению условия. Нижняя полускобка соответствует невыполнению условия, т.е. » нет » Р ( а > б ) ₃  5 .

Операторы получают номера индексов согласно порядка их действия. Если оператор зависит от параметров, например i, j, то он обозначается так 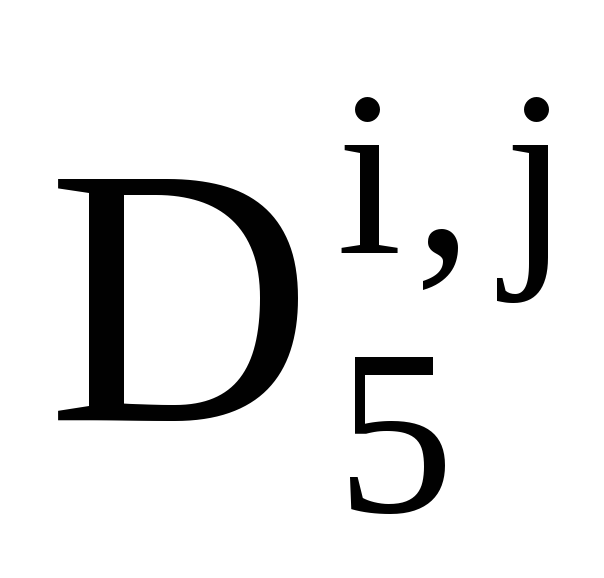и т.д. Условие записывается в виде функции, где в скобках указывается соответсвующее условие. Варьирующие изменяют параметры V ( i,j ). Операторная схема алгоритма Евклида имеет вид:

Источник

Информатика

Именная карта банка для детей
с крутым дизайном, +200 бонусов

Закажи свою собственную карту банка и получи бонусы

План урока:

Способы решения задач по логике

Многие задачи можно решить, используя инструменты алгебры логики. Чтобы получить результат, можно пойти 3 путями:

• рассуждая над условием;
• решая логические операции;
• используя таблицы истинности.

Логический подход подразумевает перевод условия из естественного языка на язык символов, схем и формул. Для такой формализации высказываний нужно выполнить ряд шагов.

Этапы решения логических задач:

• Разобраться с условием на естественном языке, выделив простые высказывания, и дать им символьные обозначения (латиница).
• Записать условие в виде формулы. Решить ее поэтапно, упрощая, учитывая приоритеты (( ), ¬, &, V).
• Просчитать формулы строчно или при помощи таблиц истинности, учитывая законы алгебры логики.
• Проверить, соответствует ли полученный результат условию задачи.

Табличный способ – этапы, особенности

Таблица истинности – табличное выражение результата логических операций для каждого отдельного набора значений переменных.

Такие таблицы позволяют абстрагироваться от маловажной информации, сосредоточиться только на связях между исходными данными, над происходящими процессами. Таким образом, человек может абстрагироваться от непонятной для него информации, решать неспецифические задачи.

Метод таблиц

Чтобы использовать таблицы истинности, необходимо формализовать условие, то есть отойти от деталей задачи, обозначая первоначальную информацию при помощи букв и цифр 0 и 1.

Существует общий алгоритм построения таблиц:

• Определить число логических значений/переменных (n) в примере.
• Установить вид, число и тип операций. Важно заранее определить очередность действий, выразить это при помощи скобок.
• Полученные данные позволяют рассчитать сколько нужно столбцов – это сумма числа переменных и операций.
• Нарисовать таблицу, заполнить шапку, записав обозначение переменных и выбранные действия.
• Определить, сколько существует наборов логических переменных (т.е. число строчек) по формуле m = 2 n + 1 (шапка).
• Заполнить столбцы, вписав наборы значений логических переменных (0 или 1).
• Записать результаты логических операций, указанных в шапке для каждой совокупности значений.
• Сделать выводы на основании полученных результатов.

Если необходимо перебрать все значения простых выражений, то для задач:

• с 2-мя переменными может быть только 4 набора логических переменных;

Если словесно описывать все эти комбинаций, на каждый из примеров понадобится десятки строк текста.

Обязательно учитывают приоритет операций:

• Указанные в скобках.
• Отрицание.
• Логическая конъюнкция чисел.
• Дизъюнкция.
• Строгая дизъюнкция.
• Импликация.
• Эквивалентность.

Обозначение логических операций:

Сравнение методов решения

Метод рассуждений

Он заключается в пошаговом анализе условий с промежуточными выводами на каждом этапе. Выполняется анализ таблицы истинности каждого логического выражения.

Пример №1.

Андрей, Владимир, Георгий и Дмитрий живут на одной улице, они соседи. Они работают по таким специальностям: гитарист, плотник, егерь и стоматолог.

• дом плотника правее егеря;
• стоматолог проживает левее егеря;
• дом гитариста с самого краю;
• стоматолог живет рядом с гитаристом;
• Владимир не гитарист, и его дом не соседствует с гитаристом;
• дома Дмитрия и егеря соседние;
• здание, в котором прописан Андрей, правее стоматолога;
• между домами Андрея и Дмитрия один дом.

Чтобы рассуждать было проще, добавим изображение зданий, присвоим им номера:

Но стоматолог живет левее егеря, а правее егеря – плотник. Получается, что дом гитариста не может быть последним, а дом стоматолога не может быть предпоследними. То есть, егерь живет в предпоследнем доме:

Между домами Андрея и Дмитрия стоит один дом, значит, дом Андрея не может быть предпоследним, получается номер – 4, что автоматом исключает проживание там Дмитрия и Владимира.

Условие задачи заняло 2 предложения, а рассуждений получилось на 2 страницы.

Такой подход лучше не использовать, если условие сложное или много данных.

Табличный метод

Более удачным подходом к решению задач с большим количеством данных (несколько множеств), считается табличный, или графический (диаграммы).

Чтобы построить таблицу истинности логических выражений, следует:

• Разбить задачу на простейшие утверждения, которые обозначить символами (большие буквы латинского алфавита).
• Записать условие задачи, как составное выражение из символов логических операций.
• Нарисовать таблицу истинности для полученных данных.
• Выбрать такой вариант, при котором полученные значения подходят под условие.
• Проверить соответствие выбранного варианта и условия задачи.

Чтобы преобразовывать условие задачи в логические выражения и операции, удобно пользоваться такой сводной таблицей истинности логических операций:

Рассмотрим тот же пример.

Определяем, что только гитарист может жить в первом доме, далее смотрим на заметки и условия и получаем таких жителей:

Метод компактнее, для некоторых задач нагляднее.

Построение таблиц истинности для различных типов задач

Несмотря на многообразие задач, многие условия повторяются, если оставить сухие формулы, не вникая в имена, места, профессии. Разобравшись с примером один раз, можно решать аналогичные задачи без труда. Рассмотрим несколько любопытных заданий, решив при помощи логически.

Пример 2.

Известно, что если первый студент летал в Англию на стажировку, то и второй тоже летал, но неправда, что если летал третий, то и второй.

Разобьём условие на 3 простые высказывания, присвоим им буквенные обозначения:

А — «Первый студент летал в Англию»;

В — «Второй студент летал в Англию»;

С — «Третий студент летал в Англию».

Запишем выясненные данные при помощи логических операций:

Пример 3.

Есть три 8-ых класса (А, В, С), которые соревнуются между собой за средний бал. Учителя в начале года сделали такие предположения:

• Если А получит максимальный бал, то максимальный бал получат Ви С.
• А и С получат или не получат максимальный бал одновременно.
• Необходимым условием получения высшего бала С класса является получение высшего бала В классом.

По завершении года оказалось, что 2 предсказания оказались верными, а одно – ошибочным.

Выясним, какие же классы добились высшего бала.

Разбиваем условие задачи на элементарные высказывания:

А – «А добьется высшего бала»;

В – «В добьется высшего бала»;

С – «С добьется высшего бала».

Запишем логические операции, описанные в примере:

Мы заполнили таблицу истинности для всех возможных значений исходных данных. В примере говорилось, что только 2 утверждения в конце года казались истинными, а 1- ложным. Такому условию отвечает 3-я строка в таблице.

Пример 4.

Во время знакомства девушка, любительница загадок, сказала, что ее имя узнать легко:

• последняя – гласная (Х1);
• или первая буква согласная (Х2)
• вторая – согласная (Х3).

Предложенные имена: Арина, Артур, Кэтрин, София.

Решим задачу, используя таблицу.

Сначала решим пошагово, выполняя операции по приоритету:

Указанному условию соответствует первое имя.

Пример 5.

Попробуем решать задачи, в которые нет четких высказываний, истинных или ложных. В них половина информации, правда, половина – ложь, при этом неизвестно, какая именно. Под такой тип задач можно подставить любое условие, но научившись решать его, можно разобраться со всеми аналогичными.

Известно, что в олимпиаде по химии участвовали 4 ученицы 8 класса: Марина, Света, Саша и Галя. Они заняли первые 4 места. Какое место заняла каждая из девочек, если есть их высказывания о победителях, но в них лишь половина информации правдива – первая или вторая половина предложения.

Маша Марина: «Саша заняла второе место, а Света – первое».

Полина Света: «Нет, это не так, Саша – победительница, а Галя, – на втором месте».

Ольга Саша: «Зачем вы всех путаете? Третье место за Мариной, а Света – на четвертом месте».

Составляем таблица для перебора вариантов. Правду обозначаем «1», ложь – «0».

Берем любое (Марины) утверждение и принимаем его первую часть за правду. Значит, Саша – 2 место, тогда Света не 1-ое (вторая половина фразы – ложь), остальных девочек на 2 место ставим «0».

Берем утверждение второй девочки. Так как Саша не может быть победительницей, то в этой фразе первая часть – ложь, а вторая должна быть истинной. Но в нем и вторая часть – неверна (второе место за Сашей, мы так приняли в начале).Уже на второй фразе получается противоречие всему.

Итог: Победительницей олимпиады стала Светлана, на втором месте – Галина, на третьем – Марина, на последнем из четырех – Александра.

Построение электронных схем, реализующих логические операции

Если рассмотреть электросхемы с точки зрения логики, особенно компьютерные, то их также можно описать при помощи «1» и «0» – электричество идет или не идет по проводам.

Попробуем нарисовать логические элементы схемы питания лампочки для нескольких простых операций.

Электросхема с конъюнктором

Рассмотрим все варианты:

• Все контакты включены, тогда источник света горит.
• Первый контакт в положении «выключено» – свет не горит.
• Второй контакт выключен – лампа не светит.
• Все контакты отключены – свет не горит.

Заключение – эта электрическая цепь реализует операцию «И».

Дизъюнктор, схема электропитания

Рассмотрим этот вид электрической цепочки:

• Все контакты включены – лампа горит.
• Первый контакт включен, второй выключен – свет горит.
• Обратная ситуация – выключен первый, включен второй – лампа светится.
• Все контакты выключены – света нет.

Заключение – такой вид электросхем соответствует логической операции «ИЛИ».

Инвертор в электросхемах

В этой схеме переключатель не ручной, а автоматический. Здесь процесс обратный – когда ток не идет, контакты замыкаются, горит свет. Если же в сеть подается электричество, пластинка размыкается вследствие электромагнитной индукции, и сеть разъединяется – света нет.

Заключение: схема соответствует логической операции «НЕ».

Умение читать и решать логические операции, строить соответствующие электросхемы, позволяет создавать иерархически более сложные конструкции, которые используются для реализации процессов в современных ПК.

Обозначение логических элементов

Удобно создавать электросхемы в ПО SmartNotebook, которое используется с интерактивной доской.

Источник