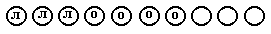Решение 3 способами решения задач

СПОСОБЫ РЕШЕНИЯ ЗАДАЧ

Понятие “решение задачи” можно рассматривать с различных точек зрения: решение как результат, т.е. как ответ на вопрос, поставленный в задаче, и решение как процесс нахождения этого результата.

С точки зрения методики обучения решению задач на первый план выступает процесс нахождения результата, который в свою очередь, тоже можно рассматривать с различных точек зрения Во-первых, как способ нахождения результата и, во-вторых, как последовательность тех действий, который входят в тот или иной способ.

Восемь яблок разложили по 2 на несколько тарелок. Сколько понадобилось тарелок?

Учащиеся могут решить эту задачу, не имея никакого представления о делении и о записи этого действия, а только опираясь на свой жизненный опыт и владея счетом от 1 до 8. Для этого они отсчитывают 8 яблок, положат 2 на одну тарелку, затем 2 на другую и т.д. пока не разложат все. Посчитав количество тарелок, они ответят на поставленный вопрос. Такой способ и называется практическим или предметным. Его возможности ограничены, так как учащийся может выполнить предметные действия только с небольшим количеством предметов. Усвоив смысл действия деления и его запись, можно решить эту задачу уже не практическим, а арифметическим способом, записав равенство 8 : 2 = 4.

Для решения можно применить алгебраический способ, рассуждая при этом так: “Число тарелок неизвестно, обозначим их буквой Х. На каждой тарелке 2 яблока, значит число всех яблок — это 2х. Так как в условии известно, что число всех яблок 8, то можно записать уравнение 2х = 8 и решить его х = 8 : 2, х = 4”.

Задачи, в которых для ответа на вопрос нужно выполнить только одно действие, называются простыми. Если для ответа на вопрос задачи нужно выполнить два и более действий, то такие задачи называются составными. Составную задачу, так же как и простую можно решить, используя различные способы.

Рыбак поймал 10 рыб. Из них 3 леща, 4 окуня, остальные щуки. Сколько щук поймал рыбак?

Обозначим каждую рыбу кругом. Нарисуем 10 кругов и обозначим

пойманных рыб: л — лещи, о — окуни.

Для ответа на вопрос задачи можно не выполнять арифметические действия, так как количество пойманных щук соответствует тем кругам, которые не обозначены (их З).

1) 3 + 4 = 7 (р.) — пойманные рыбы

Для ответа на вопрос задачи мы выполнили два действия.

Пусть х — пойманные щуки

Тогда количество всех рыб можно записать выражением:

3 + 4 + х — все рыбы

По условию задачи известно, что рыбак поймал всего 10 рыб.

Значит 3 + 4 + х = 10

Решив это уравнение, мы ответим на вопрос задачи.

Этот способ, так же как и практический, позволяет ответить на вопрос задачи, не выполняя арифметических действий.

В начальных классах используются различные формы записи решения задач по действиям, по действиям с пояснением, с вопросами, выражением.

У мальчика было 90 книг. 28 он поставил на первую полку, 12 на вторую. Остальные на третью. Сколько книг на третьей пилке?

а) решение по действиям

Ответ: 50 книг на третьей полке.

б) по действиям с пояснением

1) 28 + 12 = 40 (к.) на 1 и 2 полках вместе.

2) 90 — 10 = 50 (к.) на 3 полке.

1) Сколько книг на первой и второй полках вместе?

2) Сколько книг на третьей полке?

При записи решения задачи выражением можно вычислить его значение. Тогда запись решения задачи будет выглядеть так:

Читайте также: Способ применения витамина с 500
90 — (28 + 12) = 50 (к.)

Не следует путать такие понятие как: решение задачи различными способами (практический, арифметический графический, алгебраический), различные формы записи арифметического способа, решения задачи (по действиям, выражением по действиям с пояснением, с вопросами) и решение задачи различными арифметическими способами. В последнем случае речь идет о возможности установления различных связей между данными и искомым, а, с следовательно, о выборе других действий или другой их последовательности для ответа на вопрос задачи.

Например, рассмотренную выше задачу можно решить другим арифметическим способом:

1) 90 — 28 = 62 (к.) на 2 и3 полках.

2) 62 — 12 = 50 (к.) на 3 полке.

В качестве арифметического способа можно рассматривать и такое решение данной задачи:

1) 90 — 12 = 78 (к.) на 2 и 3 полках.

2) 78 -28 = 50 (к.) на З полке.

В числе способов решения задач ложно назвать схематическое моделирование. В отличие от графического способа, который позволяет ответить на вопрос задачи, используя счет и присчитывание схема моделирует только связи и отношения между данными и искомыми. Эти отношения не всегда возможно, а порой даже нецелесообразно представлять в виде символической модели (выражение, равенство) Тем не менее моделирование текста задачи в виде схемы иногда позволяет ответить не вопрос задачи.

Когда из гаража выехало 18 машин, в нем осталось в 3 раза меньше, чем было. Сколько машин было в гараже?

Решение этой задачи арифметическим способом довольно сложно для ребенка. Но если использовать схему, то от нее легко перейти к записи арифметического действия. В этом случае запись решения будет иметь вид:

Ответ: 27 машин было в гараже

В альбоме для раскрашивания 48 листов. Часть альбома Коля раскрасил. Сколько листов осталось не раскрашенными, если Коля раскрасил в 2 раза больше, чем ему осталось?

Решение задачи можно оформить так:

48 : 3 = 16 (л.) Ответ: 16 листов

[../../../_private/navbar1.htm]

Источник

Математика. 3 класс

Конспект урока

Математика, 3 класс

Урок № 38. Решение задач несколькими способами

Перечень вопросов, рассматриваемых в теме:

Какие способы можно использовать при решении текстовых задач?

В решении каких задач нужно использовать правило умножения суммы на число?

В решении каких задач нужно использовать правило деления суммы на число?

Глоссарий по теме:

Задача – математический рассказ с неизвестным.

Схема – краткое условие задачи.

Обязательная литературы и дополнительная литература:

Моро М. И., Бантова М. А. и др. Математика 3 класс. Учебник для

общеобразовательных организаций М.; Просвещение, 2017. – с. 18.

М. И. Моро, С.И.Волкова. Для тех, кто любит математику 3 класс. Учебное пособие для общеобразовательных организаций. М.; Просвещение,2018. – с. 12.

Теоретический материал для самостоятельного изучения

Ребята, давайте вспомним, что такое задача.

Задача – это рассказ, в котором требуется что-либо узнать.

Чтобы ответить на вопрос задачи, нужно, понять, о чём в ней говориться, представить ситуацию, описываемую в задаче.

Читать условие нужно внимательно: частями, предложениями.

Чтобы легче было представить то, о чём говорится в задаче, можно сделать рисунок (условный рисунок), построить чертёж (схематический чертёж), выполнить краткую запись, составить таблицу. Это поможет установить зависимость между данными задачи.

Из графических моделей видно, что показывает каждое число, что неизвестно, можно ли сразу ответить на вопрос задачи, если нет, то почему. Составляем план решения задачи, который представляет собой цепочку из последовательных действий.

Записывать решение задачи можно по действиям, с пояснениями, с вопросом к каждому действию или выражением.

После проверки решения задачи, записываем ответ.

Ответ нужно списывать с вопроса. Ответ всегда начинается с числа.

Выбор способа решения задачи зависит от условия задачи и данных.

Выполним тренировочные задания:

1. Решим задачу: «В корзине лежало 10 яблок и 6 груш. Фрукты разложили поровну в 2 вазы. Сколько в одной вазе?»

Читайте также: Народные способы лечения дивертикулеза
Решение: (10 + 6) : 2 = 8 штук.

2. Найдите и выделите цветом по вертикали и горизонтали в филворде компоненты задачи

Миша пришил в первый день 12 пуговиц, ещё два дня по 5 пуговиц.;

Сколько пуговиц всего пришил Миша?;

12 + 5 ∙ 2;

22 пуговицы.

Слова, которые нужно найти: условие; вопрос; решение; ответ.

3. Решите задачу и выберите правильный ответ: «У Зои 20 открыток с природой и 6 открыток с животными, у Веры 15 открыток с цветами и 15 открыток с городами, а у Алёны в 7 раз меньше, чем у обеих подружек. Сколько открыток у Алёны?»

Источник

Способы решения задач за 3 класс

ЗАДАЧИ НА УМНОЖЕНИЕ (714 -747)

1. На 3 полках по 2 книги. Сколько всего книг на трёх полках?

1. Р е ш е н и е .

1)Если даны 3 полки и на каждой полке по две книги, то всего на полках будет 2 х 3 = 6 книг.

О т в е т: на трёх полках будет 6 книг.

2. (725) Сколько литров в 9 двухлитровых банках?

1)Ели даны 9 банок и каждая банка по 2 литра, то всего будет 9 х 2 = 18 литров.

О т в е т: всего 18 литров

3. (739) В магазине было 6 ящиков конфет по 6 кг в каждом. Сколько всего килограммов конфет было в магазине?

1)Если в магазине было 6 ящиков конфет и в каждом ящике 6 кг, то всего в магазине было 6 х 6 = 36 кг конфет

О т в е т: всего в магазине было 36 кг конфет.

1. Какое действие называется умножением?

Умножением называется прямое арифметическое действие, с помощью которого находят сумму одинаковых слагаемых (количество единиц в одинаковых слагаемых).

2 х 3 = 2 + 2 + 2 = 3 + 3 = 6

2. Как называются компоненты действия умножения?

Компоненты действия умножения называются сомножителями. Первая компонента называется первым сомножителем (множимое), вторая — вторым сомножителем (множитель). Результат действия умножения называется произведением.

3. Какая таблица называется таблицей умножения?

Таблицей умножения называется такая таблица, в каждой ячейке которой стоит произведение двух чисел, расположенных в первом столбце и первой строке.

Рис.2. Таблица умножения

Правило умножения задаётся таблицей умножения, которая основывается на таблице сложения. Произведение двух чисел с помощью таблицы умножения можно найти с помощью двух стрелок перпендикулярных сторонам таблицы 2 х 3 = 6.

В первом столбце первый сомножитель m, в верхней строке второй n. В остальных ячейках таблицы соответствующее значение произведение k = m х n. С помощью таблицы умножения можно найти результат произведение с помощью двух стрелок.

2. ЗАДАЧИ НА УВЕЛИЧЕНИЕ ИЛИ УМЕНЬШЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ (№748 – 784)

ЗАДАЧИ НА УВЕЛИЧЕНИЕ ИЛИ УМЕНЬШЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ (№748 – 784)

1. На первой полке 3 книги, а на второй в 4 раза больше. Сколько книг на второй полке? Сколько всего книг на двух полках?

1)Если на первой полке три книги, а на второй в 4 раза больше, то на второй полке будет 3 ´ 4 = 12 книг.

2) Если на первой полке три книги, а на второй 12 книг, то на обоих полках будет 3 +12 =15 книг.

О т в е т: на второй полке 12 книг; на обоих полках 15 книг.

3. ЗАДАЧИ НА ДЕЛЕНИЕ ( №785-820)

ЗАДАЧИ НА ДЕЛЕНИЕ ( 785-820)

1. На 3 полках 12 книг, причём поровну. Сколько книг на каждой из полок?

S1: даны 3 полки

S2: всего 12 книг

S3: на полках книг поровну

1)Если даны 3 полки и на них 12 книг и поровну, то на каждой из полок будет 12 : 3 = 4 книги.

О т в е т: на каждой из полок было 4 книги

2. На полках 12 книг, поровну. На каждой полке по 2 книги. Сколько полок?

1. Если на полках 12 книг поровну и на каждой полке по 2 книги, то ввсего полок

Читайте также: Признаки необычного выполнения присущи следующим способам технической подделки подписи
2. 12: 2 = 6 полок.

О т в е т: на 6 полоках

3 (789) У двух мальчиков 6 карандашей поровну. Сколько карандашей у каждого мальчика?

1)Если у 2 мальчиков 6 карандашей поровну, то у каждого было 6: 3 =2 карандаша

О т в е т: у каждого было по 2 карандаша.

1. Какое действие называется делением?

Делением называется арифметическое действие обратное умножению, с помощью которого по заданному произведению и одному известному множителю находят другой неизвестный множитель.

2. Как называются компоненты действия деления?

Первая компонента действия деления называется делимым. Вторая компонента называется делителем. Результат действия деления называется частным.

Способ нахождения неизвестного сомножителя с помощью таблицы умножения. Если неизвестно первый сомножитель, то имеем равенство, в котором х × 3 = 6 первая компонента неизвестна. Тогда по таблице умножения находим в первой строке 3 и двигаемся вниз до 6, а затем влево и находим 2. Если неизвестна вторая компонента 2 × х = 6, то двигаемся вправо и вверх.

4. ЗАДАЧИ НА КРАТНОЕ СРАВНЕНИЕ (№821-855)

ПРОСТЫЕ ЗАДАЧИ НА КРАТНОЕ СРАВНЕНИЕ ( 821-855)

1. На первой полке 4 книги, а на второй 12. Во сколько раз книг на второй полке больше, чем на первой?

1. Р е ш е н и е .

1)Если на первой полке 4 книги, а на второй 12, то на второй полке книг больше, чем на первой в 12 : 4 = 3 раза.

О т в е т: в 3 раза книг на второй полке больше, чем на первой

2. (823) Володя нашёл 18 белых грибов, а его брат 2 гриба. Во сколько раз больше нашёл грибов Володя, чем его брат?

1)Если Володя нашёл 18 белых грибов, а его брат 2 гриб, то Володя нашёл грибов больше в 18 :2 = 9 раз?

О т в е т: Володя нашёл грибов больше, чем брат в 9 раз

5. КОСВЕННАЯ ФОРМА ЗАДАЧ НА УВЕЛИЧЕНИЕ ИЛИ УМЕНЬШЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ (№856- 891)

ЗАДАЧИ НА УВЕЛИЧЕНИЕ ИЛИ УМЕНЬШЕНИЕ ЧИСЛА В НЕСКОЛЬКО РАЗ (косвенная форма) (№856- 891)

1. На второй полке 6 книг, это в 2 раза больше, чем на первой. Сколько книг на первой полке?

1) Если на второй полке в 2 раза больше книг, чем на первой, то на первой полке в 2 раза меньше книг, чем на второй.

2)Если на второй полке 6 книг, а на первой в 2 раза меньше, то на первой полке будет 6 : 2 =3 книги.

О т в е т: на первой полке будет 3 книги.

2. (859) У брата 18 фломастеров. Это в 2 раза больше чем у его сестры. Сколько фломастеров у его сестры?

1)Если у брата было фломастеров в 2 раза больше чем у сестры, то у сестры было в 2 раза меньше чем у брата.

2)Если у брата 18 фломастеров , а у сестры в 2 раза меньше чем у брата, то у сестры было 18 : 2 = 9 фломастеров.

О т в е т: у сестры было 18 : 2 = 9 фломастеров.

3. (862) В одном кружке занималось 4 мальчика, что в 2 раза, меньше, чем во втором. Сколько мальчиков во втором кружке? Сколько всего мальчиков в двух кружках?

1)Если в одном кружке занималось 4 мальчика и это 2 раза, меньше, чем в другом, то во втором кружке занималось в 2 раза больше мальчиков.

2) Если в одном кружке занималось 4 мальчика а во втором 2 раза больше, то во втором кружке занималось 4 ´ 2 = 8 мальчиков.

3) Если в одном кружке занималось 4 мальчика, а во втором 8 мальчиков, то в двух кружках занималось 4 + 8 = 12 мальчиков.

О т в е т: в двух кружках занималось 4 + 8 = 12 мальчиков.

Источник