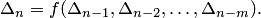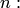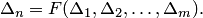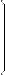Рекуррентный способ вычисления определителя

Вычисление определителей с помощью рекуррентных уравнений

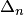
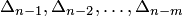
Этот метод заключается в том, что исходный определитель n-го порядка выражается через определители того же вида, но меньшего порядка. Получается рекуррентное уравнение

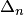
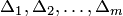
Решая это уравнение, находим формулу, выражающую определитель через определители и порядок

В последнюю формулу подставляем определители 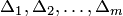невысокого порядка, которые нетрудно вычислить каким-либо другим способом.

Треугольная матрица

Треугольная матрица — в линейной алгебре квадратная матрица, в которой все элементы ниже или выше главной диагонали равны нулю.

Пример верхнетреугольной матрицы

Верхнетреугольная матрица — квадратная матрица, в которой все элементы ниже главной диагонали равны нулю.

Нижнетреугольная матрица — квадратная матрица, в которой все элементы выше главной диагонали равны нулю.

Унитреугольная матрица (верхняя или нижняя) — треугольная матрица, в которой все элементы на главной диагонали равны единице.

Треугольные матрицы используются в первую очередь при решении линейных систем уравнений, когда матрица системы сводится к треугольному виду используя следующую теорему:

Любую ненулевую матрицу 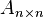путём элементарных преобразований над строками и перестановкой столбцов можно привести к треугольному виду.

Любая квадратная матрица, имеющая отличные от нуля главные миноры, представима произведением двух матриц: верхнетреугольной, и нижнетреугольной. Разложение единственно, если фиксированы (заранее оговорены) элементы главной диагонали одной из них.

Решение систем линейных уравнений с треугольной матрицей (обратный ход) не представляет сложностей.

Свойства

• Определитель треугольной матрицы равен произведению элементов на её главной диагонали .
• Определитель унитреугольной матрицы равен единице.
• Множество невырожденных верхнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается UT(n, k) или UT_n (k).
• Множество невырожденных нижнетреугольных матриц порядка n по умножению с элементами из поля k образует группу, которая обозначается LT(n, k) или LT_n (k).
• Множество верхних унитреугольных матриц с элементами из поля k образует подгруппу UT_n (k) по умножению, которая обозначается SUT(n, k) или SUT_n (k). Аналогичная подгруппа нижних унитреугольных матриц обозначается SLT(n, k) или SLT_n (k).
• Множество всех верхнетреугольных матриц с элементами из кольца k образует алгебру относительно операций сложения, умножения на элементы кольца и перемножения матриц. Аналогичное утверждение справедливо для нижнетреугольных матриц.

Определение.

Минором M_ij к элементу a_ij определителя n-го порядка называется определитель (n — 1)-го порядка, полученный из исходного определителя вычеркиванием i-той строки и j-того столбца.

Пример 1.

Найти миноры матрицы A

A =

-4

Решение:

M22 =

-4

=

M11 =

= 1·3 — 0·0 = 3 — 0 = 3

M12 =

-4

= -4·3 — 0·2 = -12 -0 = -12

M13 =

-4

= -4·0 — 1·2 = 0 — 2 = -2

M21 =

= 7·3 — 1·0 = 21 — 0 = 21

M22 =

= 5·3 — 1·2 = 15 — 2 = 13

M23 =

= 5·0 — 7·2 = 0 — 14 = -14

M31 =

= 7·0 — 1·1 = 0 — 1 = -1

M32 =

-4

= 5·0 — 1·(-4) = 0 + 4 = 4

M33 =

-4

= 5·1 — 7·(-4) = 5 + 28 = 33

Определение.

Алгебраическим дополнением A_ij к элементу a_ij определителя n-го порядка называется число

Источник

VMath

Инструменты сайта

Основное

Навигация

Информация

Действия

Содержание

Вспомогательная страница к разделу ОПРЕДЕЛИТЕЛЬ

Приемы вычисления определителей, зависящих от параметров

Довольно часто на практике возникает необходимость вычислять определители, элементы которых зависят от параметров. Метод Гаусса оказывается не слишком приспособленным для такой задачи.

Пример. Вычислить

Решение. Разложение по общей формуле даст величину этого определителя в виде полинома от $ <\color\alpha > $. С другой стороны, если для его вычисления мы попытаемся применить метод Гаусса, то на первом же шаге элементы преобразованного определителя окажутся дробно–рациональными функциями от параметра $ <\color\alpha > $. Понятно, что после приведения определителя к треугольному виду и перемножения стоящих на диагонали дробей мы, в конце концов, получим тот же ответ полиномиального вида, но сам факт, что для его получения потребовалось «выйти за пределы» множества полиномиальных функций не свидетельствует в пользу метода Гаусса… ♦

Выделение линейных множителей

Этот прием основан на свойстве полиномиальности определителя как функции его элементов. Если элементы зависят — также полиномиально — от одного параметра, то можно попытаться определить линейные множители «полинома из ответа»: иногда из особенностей определителя очевидно при каких значениях параметра этот определитель обращается в нуль.

Пример. Вычислить определитель

$$\left|\begin 1&1&1&\dots&1\\ 1&2-x&1&\dots&1\\ 1&1&3-x&\dots&1\\ \vdots& & &\ddots&\vdots\\ 1&1&1&\dots&n+1-x \end\right|.$$

Решение. Ответом в этой задаче должен быть полином по $ x_<> $. Обозначим его $ F(x)_<> $ и попробуем догадаться какие корни он может иметь. Обратим внимание на структуру определителя. Если положить $ x=1_<> $, то вторая строка будет одинаковой с первой, на основании свойства 3 определителя, при этом значении $ x_<> $ будем иметь $ F(1)=0 $. Аналогично убеждаемся, что $ F(2)=0, \dots, F(n)=0 $. Итак, на основании теоремы Безу, имеем: $$ F(x) \equiv F_1(x) (x-1)\times \dots \times (x-n) \ , $$ где через $ F_1(x) $ обозначен полином, являющийся частным от деления $ F(x)_<> $ на произведение линейных множителей. Оценим степень полинома $ F(x)_<> $. Очевидно, что при разложении определителя по общей формуле из определения, каждое слагаемое представляет произведение элементов определителя и будет полиномом по $ x_<> $. В каждом слагаемом максимально возможная степень может быть достигнута если каждый элемент в произведении будет иметь максимально возможную степень — в нашем случае равную $ 1_<> $. Отсюда с неизбежностью следует, что самым «большим» по степени может быть только главный член определителя, т.е. произведение элементов его главной диагонали: $$ F(x) \equiv 1\cdot (2-x)\times \dots \times (n+1-x) + \dots \ , $$ где многоточия скрывают все оставшиеся слагаемые полного разложения определителя и имеют степени меньшие степени выделенного слагаемого. Выделяем из этого слагаемого степень $ x_<> $: $$ F(x) \equiv (-1)^n x^n + \dots \ . $$ Мы получили оценку степени $ F(x)_<> $ вместе с выражением для его старшего коэффициента.

Ответ. $ (-1)^ (x-1)\times \dots \times (x-n) $.

Пример. Вычислить определитель

Решение. Если к первому столбцу прибавить остальные, то обнаружится, что определитель делится на $ x+y+z $; если к первому столбцу прибавить второй и вычесть третий и четвертый, то выделится множитель $ y+z-x $; если к первому столбцу прибавить третий и вычесть второй и четвертый, то выделится множитель $ x-y+z $; наконец, если к первому столбцу прибавить четвертый и вычесть второй и третий, то выделится множитель $ x+y-z $. Считая $ x,y,z $ независимыми переменными, заключаем, что все эти четыре множителя попарно взаимно просты, и значит, определитель — как полином от $ x,y,z $ — делится на их произведение $ (x+y+z)(y+z-x)(x-y+z)(x+y-z) $.

Это произведение содержит член $ z^4 $ с коэффициентом $ (-1) $, а сам определитель содержит тот же член с коэффициентом $ +1 $. Следовательно, $$ D=-(x+y+z)(y+z-x)(x-y+z)(x+y-z) =x^4+y^4+z^4-2x^2y^2-2x^2z^2-2y^2z^2 \ . $$

Метод рекуррентных соотношений

Основная идея метода заключается в том, что некоторые определители можно свести к вычислению определителей, имеющих аналогичный вид, но меньший порядок. Если удается установить вид этой зависимости в виде явной формулы, то эта формула — последовательным ее применением — позволит нам «спуститься» к определителям малых порядков.

Пример. Вычислить определитель

$$D_n=\left|\begin a_1&x&x&\dots&x\\ x&a_2&x&\dots&x\\ x&x&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&a_n \end\right|.$$

Решение. Представив элемент в правом нижнем углу в виде $ a_n=x+(a_n-x) $, можем определитель $ D_n $ разбить на сумму двух определителей: $$D_n=\left|\begin a_1&x&x&\dots&x\\ x&a_2&x&\dots&x\\ x&x&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&x \end\right|+\left|\begin a_1&x&x&\dots&0\\ x&a_2&x&\dots&0\\ x&x&a_3&\dots&0\\ \vdots&&&\ddots&\vdots\\ x&x&x&\dots&a_n-x \end\right|.$$ В первом определителе последний столбец вычтем из остальных, а второй определитель разложим по последнему столбцу: $$D_n=x(a_1-x)(a_2-x)\times\dots\times(a_-x)+(a_n-x)D_\ .$$ Это и есть рекуррентное соотношение. Подставляя в него аналогичное выражение для $ D_ $, найдем $$\begin D_n=x(a_1-x)(a_2-x)\times\dots\times(a_-x)+\\ +x(a_1-x)(a_2-x)\times\dots\times(a_-x)(a_n-x)+D_(a_-x)(a_n-x). \end$$ Повторяя то же рассуждение $ n-1 $ раз и замечая, что $ D_1=a_1=x+(a_1-x) $, найдем $$\begin D_n=x(a_1-x)(a_2-x)\dots(a_-x)+x(a_1-x)\times\dots\times(a_-x)(a_n-x)+\dots+\\ +x(a_2-x)\times\dots\times(a_n-x)+(a_1-x)(a_2-x)\times\dots\times(a_n-x)=\\ \displaystyle =x(a_1-x)(a_2-x)\times\dots\times(a_n-x)\left( \frac<1>+\frac<1>+\dots+\frac<1>\right). \end$$

$$\left|\begin a_1b_1&a_1b_2&a_1b_3&\dots&a_1b_n\\ a_1b_2&a_2b_2&a_2b_3&\dots&a_2b_n\\ a_1b_3&a_2b_3&a_3b_3&\dots&a_3b_n\\ \vdots&&&&\vdots\\ a_1b_n&a_2b_n&a_3b_n&\dots&a_nb_n \end\right|.$$

Ответ. $ \displaystyle a_1b_n\prod_^(a_b_j-a_jb_) $ .

Пример. Вычислить определитель

$$D_n=\left|\begin a_1&x&x&\dots&x\\ y&a_2&x&\dots&x\\ y&y&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ y&y&y&\dots&a_n \end\right|.$$

Решение начинается тем же приемом, что и в предыдущем примере: $$ D_n= \left|\begin a_1&x&x&\dots&x\\ y&a_2&x&\dots&x\\ y&y&a_3&\dots&x\\ \vdots&&&\ddots&\vdots\\ y&y&y&\dots&x \end\right|+(a_n-x)D_=x(a_1-y)(a_2-y)\times \dots \times (a_-y)+(a_n-x)D_ \ . $$ Можно было бы идти по проторенному пути и «разделывать» определитель $ D_ $ с использованием уже полученной формулы. Имеется, однако, более эффективный прием. Заметим, что начальный определитель симметричен относительно вхождения параметров $ x_<> $ и $ y_<> $, и эта симметрия должна проявляться в окончательном ответе. Следовательно, наряду с полученным выражением, будет справедливо и следующее: $$ D_n=y(a_1-x)(a_2-x)\times \dots \times (a_-x)+(a_n-y)D_ \ , $$ произведенное перестановкой параметров $ x \leftrightarrow y $. В результате мы получаем систему уравнений для определения двух неизвестных величин $ D_ $ и $ D_ $. Решаем эту систему относительно $ D_n $ (например, по формулам Крамера): $$ D_n = \frac<\displaystyle y\prod_^n(a_k-x)-x\prod_^n(a_k-y)> \ . $$ ♦

В примере следующего пункта метод рекуррентных соотношений комбинируется с методом выделения линейных множителей.

Определитель Вандермонда

Подробнее о матрице, определителе Вандермонда и их применении ☞ ЗДЕСЬ.

Пример. Вычислить определитель Вандермонда

$$ V(x_1,\dots,x_n)= \left|\begin 1 &x_1&x_1^2&\ldots&x_1^\\ 1 &x_2&x_2^2&\ldots&x_2^\\ \vdots& &&& \vdots\\ 1 &x_n&x_n^2&\ldots&x_n^ \end\right|_ $$

Решение. Поясним идею для случая $ n=4 $. Выражение для $ V(x_1,x_2,x_3,x_4) $ — если его формально разложить по общей формуле — будет полиномом относительно своих переменных. Рассмотрим его как полином от переменной $ x_4 $, которую — для удобства — временно переобозначим через $ x $: $$ \tilde V(x)=\left|\begin 1 &x_1&x_1^2&x_1^3\\ 1 &x_2&x_2^2&x_2^3\\ 1 &x_3&x_3^2&x_3^3\\ 1 &x&x^2&x^3\\ \end\right| \ ; $$ оставшиеся переменные будем считать параметрами. Если подставить в этот определитель $ x=x_1 $, то определитель обратится в нуль (как имеющий одинаковые строки см. свойство 3 ☞ ЗДЕСЬ). Аналогичные рассуждения верны для $ x=x_2 $ и $ x=x_3 $. Таким образом, полином $ \tilde V(x) $ имеет корни $ x_1,x_2,x_3 $, а его степень — если разложить по последней строке — не превышает $ 3 $. Следовательно, этот полином должен иметь следующее разложение на линейные множители: $$ \tilde V(x) \equiv A(x-x_1)(x-x_2)(x-x_3) \ ; $$ при этом константа $ A $ зависит только от $ x_1, x_2,x_3 $. Выражение для нее можно найти, если сообразить, что она является старшим коэффициентом полинома $ \tilde V(x) $, т.е. коэффициентом при степени $ x^3 $. Этот коэффициент можно «извлечь» из исходного определителя — это алгебраическое дополнение элемента определителя, стоящего в правом нижнем углу, т.е. $$ \left|\begin 1 &x_1&x_1^2\\ 1 &x_2&x_2^2\\ 1 &x_3&x_3^2 \end\right| \ . $$ Но этот определитель — тот же определитель Вандермонда, только порядка меньшего исходного. Возвращая переменной $ x $ ее исходное значение, получаем рекуррентное соотношение: $$ V(x_1,x_2,x_3,x_4)\equiv V(x_1,x_2,x_3) (x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$ Раскладываем определитель в правой части по той же схеме: $$ V(x_1,x_2,x_3) \equiv \left|\begin 1 &x_1\\ 1 &x_2 \end\right| (x_3-x_1)(x_3-x_2) \equiv (x_3-x_1)(x_3-x_2)(x_2-x_1) \ . $$ Таким образом, $$ V(x_1,x_2,x_3,x_4)= $$ $$ =(x_2-x_1)(x_3-x_1)(x_3-x_2)(x_4-x_1)(x_4-x_2)(x_4-x_3) \ . $$ А в общем случае получаем ответ $$ V(x_1,\dots,x_n)= \prod_<1\le j ♦

Определитель трёхдиагональной матрицы

Более сложный пример применения метода дает задача вычисления определителя трехдиагональной матрицы, представленного в следующем виде (определитель Якоби):

$$ <\mathfrak J>_n = \left|\begin a_1 &b_1&0&0& \dots & 0 & 0\\ -c_2 &a_2&b_2&0& \dots & 0 & 0\\ 0 &-c_3&a_3&b_3& \dots & 0 & 0\\ \vdots &&& &\ddots&& \vdots \\ 0 &0&0&0& \dots & a_ & b_\\ 0 &0&0&0& \dots & -c_n & a_ \end\right|_ \ . $$ Формальное вычисление этого определителя (в соответствии с определением) даст полином по $ a_1,\dots,a_n,b_1,\dots,b_,c_2,\dots,c_n $, линейный по каждой из этих переменных. Если разложить $ <\mathfrak J>_n $ по последней строке, то получим: $$ \begin <\mathfrak J>_n&=&a_n<\mathfrak J>_+b_c_n<\mathfrak J>_ =a_n(a_<\mathfrak J>_+b_c_<\mathfrak J>_)+ b_c_n<\mathfrak J>_= \\ &=&(a_na_+b_c_n)<\mathfrak J>_+a_nb_c_<\mathfrak J>_= \dots \end $$

Пример.

$ <\mathfrak J>_2=a_1a_2+b_1c_2 $ , $ <\mathfrak J>_3=a_1a_2a_3+a_1b_2c_3+b_1c_2a_3 $, $$ <\mathfrak J>_5=a_1a_2a_3a_4a_5+b_1c_2a_3a_4a_5+a_1b_2c_3a_4a_5+a_1a_2b_3c_4a_5 +a_1a_2a_3b_4c_5+b_1c_2b_3c_4a_5+b_1c_2a_3b_4c_5+a_1b_2c_3b_4c_5 \ . $$

Теорема. Значение $ <\mathfrak J>_n $ равно сумме главного члена $ a_1a_2\times \dots \times a_ $ и всевозможных произведений, получающихся из него заменой одной или нескольких пар соседних множителей $ a_ja_ $ на $ b_jc_ $.

Частный случай определителя Якоби — континуант: $$ Q_n(x_1,x_2,\dots,x_) = \left|\begin x_1 &1&0&0& \dots & 0 & 0\\ -1 &x_2&1&0& \dots & 0 & 0\\ 0 &-1&x_3&1& \dots & 0 & 0\\ \vdots &&& &\ddots&&\vdots \\ 0 &0&0&0& \dots & x_ & 1\\ 0 &0&0&0& \dots & -1 & x_ \end\right|_ $$

Теорема. Континуант равен сумме произведения $ x_1\cdot x_2 \times \dots \times x_n $ и всевозможных произведений, получающихся из него вычеркиванием пар соседних множителей (и добавлением $ 1 $ в случае четного $ n $).

Пример.

$$ \begin Q_2(x_1,x_2)&=&x_1x_2+1 \ , \\ Q_3(x_1,x_2,x_3)&=& x_1x_2x_3+x_3+x_1 \ , \\ Q_6(x_1,x_2,x_3,x_4,x_5,x_6)&=&x_1x_2x_3x_4x_5x_6+\\ &&+x_3x_4x_5x_6 +x_1x_4x_5x_6+ x_1x_2x_5x_6+ x_1x_2x_3x_6+x_1x_2x_3x_4+ \\ &&+x_5x_6+x_1x_6+x_1x_2+x_1x_4+x_3x_4+x_3x_6+1 . \end $$

Исследуем еще один частный случай определителя Якоби — при одинаковых элементах на диагоналях $$a_1=\dots=a_n = a, \ b_1=\dots=b_ = b, \ c_2=\dots=c_n = c \ ; $$ таким образом: $$ <\mathfrak J>_n= \left|\begin a &b&0&0& \dots & 0 & 0\\ c &a&b&0& \dots & 0 & 0\\ 0 &c&a&b& \dots & 0 & 0\\ \vdots &&& &\ddots&& \vdots \\ 0 &0&0&0& \dots & a & b\\ 0 &0&0&0& \dots & c & a \end\right|_ \ . $$ В этом случае уравнение, связывающее определители трех последовательных порядков, принимает вид: $$ <\mathfrak J>_n=a<\mathfrak J>_-bc<\mathfrak J>_ \ .$$ Оно может быть решено применением общего приема решения линейного разностного уравнения.

Пример. Вычислить

$$ \left|\begin 2 &2&0& \dots & 0 & 0\\ 1 & 2 &2& \dots & 0 & 0\\ 0 &1&2& \dots & 0 & 0\\ \vdots && \ddots &\ddots&& \vdots\\ 0 &0&0& \dots & 2 & 2\\ 0 &0&0& \dots & 1 & 2 \end\right|_ \ . $$

Решение. Разностное уравнение имеет вид $ <\mathfrak J>_n=2<\mathfrak J>_-2<\mathfrak J>_ $. Cтроим соответствующее ему характеристическое уравнение и находим его корни: $ \lambda_<1,2>=1 \pm \mathbf i $. Поскольку они различны, решение разностного уравнения ищем в виде $$ C_1 (1+\mathbf i )^n+C_2 (1-\mathbf i)^n \ .$$ Для определения констант $ C_1 $ и $ C_2 $ вычислим определители первого и второго порядков: $ <\mathfrak J>_1=2,<\mathfrak J>_2=2 $. $$ \left\< \begin 2&=&C_1(1+\mathbf i)&+C_2(1+\mathbf i), \\ 2&=&C_1(1+\mathbf i)^2&+C_2(1+\mathbf i)^2 \end \right. \quad \Rightarrow \quad C_1=\frac<1-\mathbf i><2>,\ C_2=\frac<1+\mathbf i> <2>$$ Ответ. $ <\mathfrak J>_n=(1+\mathbf i)^+(1-\mathbf i)^ $.

Представление определителя в виде суммы определителей

Пример. Вычислить определитель

$$D_n=\left|\begin a_1+b_1&a_1+b_2&\dots&a_1+b_n\\ a_2+b_1&a_2+b_2&\dots&a_2+b_n\\ \dots&&&\dots\\ a_n+b_1&a_n+b_2&\dots&a_n+b_n \end\right|.$$

Решение. Определитель раскладывается по первой строке на два определителя, каждый из них по второй строке снова раскладывается на два определителя и т.д. Дойдя до последней строки, получим $ 2^n $ определителей.

Если при каждом разложении за первые слагаемые принимать числа $ a_i $, а за вторые — числа $ b_j $, то строки полученных определителей будут либо вида $ (a_i,a_i,\dots,a_i) $, либо вида $ (b_1,b_2,\dots,b_n) $. Две строки первого типа пропорциональны, а второго типа равны. При $ n>2 $ в каждый получившийся определитель попадут по крайней мере две строки одного типа, и он обратится в нуль. Таким образом, $$D_n=0 \ npu \ n>2,\ D_1=a_1+b_1,\quad D_2=\left|\begin a_1&a_1\\ b_1&b_2 \end\right|+\left|\begin b_1&b_2\\ a_2&a_2 \end\right|=(a_1-a_2)(b_2-b_1).$$

Вычислить определитель методом представления его в виде суммы определителей

$$\left|\begin x_1&a_1b_2&a_1b_3&\dots&a_1b_n\\ a_2b_1&x_2&a_2b_3&\dots&a_2b_n\\ a_3b_1&a_3b_2&x_3&\dots&a_3b_n\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ a_nb_1&a_nb_2&a_nb_3&\dots&x_n \end\right|.$$

Ответ. $$(x_1-a_1b_1)(x_2-a_2b_2)\times \dots \times (x_n-a_nb_n) \times $$ $$ \times \left(1+\frac+\frac+\dots+\frac\right) \ .$$

Увеличение порядка определителя

Пример. Вычислить определитель

$$ \det \left[ s_x-s_ \right]_^ = \left| \begin s_0x-s_1&s_1x-s_2&\dots& s_x-s_ \\ s_1x-s_2&s_2x-s_3&\dots& s_x-s_ \\ \dots & & & \dots \\ s_x-s_ & s_x-s_ & \dots & s_<2n-2>x-s_ <2n-1>\end \right|_ $$ при заданных числовых значениях $ s_0,s_1,\dots,s_ <2n-1>$.

Интерполяция

Можно считать излагаемый ниже метод обобщением приведенного выше метода выделения линейных множителей: если матрица имеет полиномиальную зависимость от параметра (параметров), то угадать корни ее определителя — также полинома от этого параметра — удается не всегда, а вот его значения при конкретных величинах параметра (параметров) всегда можно вычислить.

Попробуем решить пример, с которого начинается настоящий раздел.

Пример. Вычислить

$$ \det A(\alpha)= \left| \begin \alpha+1 &\alpha^2+1 &\alpha^2-1 &\alpha \\ \alpha^2+\alpha+1 & \alpha^2-\alpha+1 & \alpha^2 & 1 \\ 2\,\alpha+1 &\alpha^2+2 & \alpha & \alpha^2-1 \\ 2\,\alpha & 2\, \alpha^2+2\,\alpha+1 & \alpha^2-\alpha-1 & \alpha+1 \end \right| \ . $$

Решение. Поскольку каждый элемент определителя является полиномом, то, на основании определения определителя как суммы произведений его элементов, величина определителя также должна быть полиномом по $ \alpha_<> $. Обозначим этот полином через $ F(\alpha) $. Таким образом, задача сводится к вычислению степени $ \deg F $ этого полинома и его коэффициентов. Для решения первой задачи формируем новый определитель, путем вытаскивания из элементов исходного определителя их старших мономов: $$ \left| \begin \alpha &\alpha^2 &\alpha^2 &\alpha \\ \alpha^2 & \alpha^2 & \alpha^2 & 1 \\ 2\,\alpha &\alpha^2 & \alpha & \alpha^2 \\ 2\,\alpha & 2\, \alpha^2 & \alpha^2 & \alpha \end \right| \ . $$ Если этот определитель не равен нулю тождественно по $ \alpha_<> $, то его старший моном совпадает со старшим мономом $ F(\alpha) $. Новый определитель также зависит от $ \alpha_<> $, но характер этой зависимости становится менее сложным, чем у исходного, и для его вычисления можно использовать различные упрощающие соображения. Например, можно вынести общие множители элементов первого, второго и третьего столбцов (см. свойство 4 ☞ ЗДЕСЬ ) $$ =\alpha\cdot \alpha^2 \cdot \alpha \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 2 & 2 & \alpha & \alpha \end \right| = $$ Далее, вычитаем из последней строки первую, умноженную на $ 2_<> $: $$ =\alpha^4 \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 0 & 0 & -\alpha & -\alpha \end \right| =-\alpha^5 \left| \begin 1 &1 & \alpha &\alpha \\ \alpha & 1 & \alpha & 1 \\ 2 &1 & 1 & \alpha^2 \\ 0 & 0 & 1 & 1 \end \right| $$ Теперь вычтем из четвертого столбца третий: $$ =-\alpha^5 \left| \begin 1 &1 & \alpha & 0 \\ \alpha & 1 & \alpha & 1-\alpha \\ 2 &1 & 1 & \alpha^2 -1 \\ 0 & 0 & 1 & 0 \end \right| $$ и разложим определитель по последней строке: $$ = \alpha^5 \left| \begin 1 &1 & 0 \\ \alpha & 1 & 1-\alpha \\ 2 &1 & \alpha^2 -1 \\ \end \right| \ . $$ Поскольку нас интересует только лишь старший моном этого определителя, в элементах последнего столбца оставляем старшие мономы: $$ \alpha^5 \left| \begin 1 &1 & 0 \\ \alpha & 1 & -\alpha \\ 2 &1 & \alpha^2 \end \right| = \alpha^6 \left| \begin 1 &1 & 0 \\ \alpha & 1 & -1 \\ 2 &1 & \alpha \end \right| \ . $$ Этот определитель можно вычислить «вручную» (при этом, повторюсь, нас интересуют только лишь максимальные по степени $ \alpha_<> $ члены его разложения), получаем: $ — \alpha^8 $.

Итак, неизвестный полином $ F(\alpha) $ имеет степень $ 8_<> $. Для его определения у нас имеется представление этого полинома в форме определителя. При этом считается, что числовые определители мы вычислять умеем. Будем искать полином $ F(\alpha) $ как решение задачи интерполяции. Зададим произвольные числовые значения для $ \alpha_<> $ — в количестве $ 9_<> $ штук (по числу коэффициентов полинома, требующих определения), вычислим соответствующие числовые определители, составим интерполяционную таблицу: $$ \begin \alpha & \alpha_1 & \alpha_2 & \dots & \alpha_9 \\ \hline F & \det A (\alpha_1) &\det A (\alpha_2) & \dots & \det A (\alpha_9) \end $$ и вычислим $ F(\alpha) $ по одному из методов вычисления интерполяционного полинома.

На виду лежат два соображения:

1. имеет смысл в качестве чисел $ \alpha_j $ выбирать возможно минимальные по модулю;

2. поскольку мы уже знаем величину одного из коэффициентов, имеет смысл выбрать — из двух стандартных представлений интерполяционного полинома — форму Ньютона (последнее вычисление делать не придется, можно сократить число узлов интерполяции). Для настоящего примера: $$ \begin \alpha & 0 & 1 & -1 & 2 & -2 & 3 & -3 & 4 \\ \hline F & -4 & -4 & 24 &-222 & 734 & -9616 & 4388 & -98176 \end $$

Ответ. $ -\alpha^8-3\,\alpha^7+3\,\alpha^6-\alpha^5+23\,\alpha^4-7\,\alpha^3-11\,\alpha^2-3\,\alpha-4 $.

$$ B=\left( \begin 1 &2 &2 &1 \\ 2 &2 &2 & 0 \\ 1 &2 &1 & 2 \\ 1 & 2 & 2 & 1 \end \right) \ . $$ Требуется выбрать по одному элементу из каждой строки и каждого столбца этой матрицы, так, чтобы получившаяся сумма стала максимальной: $$ b_<1j_1>+b_<2j_2>+b_<3j_3>+b_ <4j_4>\quad \mbox < при различных >\quad \ < j_1,j_2,j_3,j_4\>\subset \ < 1,2,3,4 \>. $$ Иными словами, после выбора какого-то кандидата в сумму, из матрицы вычеркиваются строка и столбец его содержащие, и дальнейший выбор осуществляется в оставшейся подматрице. Задача оказывается нетривиальной уже хотя бы потому, что «жадная стратегия» выбора — когда на каждом шаге выбирается максимальный из оставшихся элементов — не приводит к правильному ответу: $$ B=\left( \begin 4 &3 \\ 3 &1 \end \right) \quad \Rightarrow \quad 4+1 1) .

Задача. Имеется $ n_<> $ работ, которые надо поручить $ n_<> $ работникам. Каждый работник может быть назначен только на одну работу, и каждая работа может быть поручена только одному работнику. Прибыль от труда работника под номером $ j_<> $ при выполнении работы под номером $ k_<> $ известна и равна $ b_ $. Как распределить работы между работниками так, чтобы прибыль стала максимальной?

Разные определители, встречающиеся в ресурсе

Источник