Реферат по математике способы вычисления интегралов

Реферат: Исследование методов вычисления определенных интегралов

УФИМСКИЙ ГОСУДАРСТВЕННЫЙ АВИАЦИОННЫЙ ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

ФИЛИАЛ В ГОРОДЕ СТЕРЛИТАМАК

КАФЕДРА ЕСТЕСТВЕННО-НАУЧНЫХ И ОБЩЕПРОФЕССИОНАЛЬНЫХ ДИСЦИПЛИН

ИССЛЕДОВАНИЕ МЕТОДОВ ВЫЧИСЛЕНИЯ ОПРЕДЕЛЕННЫХ ИНТЕГРАЛОВ

к курсовой работе по ИНФОРМАТИКЕ

Название: Исследование методов вычисления определенных интегралов Раздел: Рефераты по информатике, программированию Тип: реферат Добавлен 07:06:20 18 апреля 2011 Похожие работы Просмотров: 4372 Комментариев: 20 Оценило: 3 человек Средний балл: 4.7 Оценка: неизвестно Скачать

Группа ВТС-109	Фамилия, и. о.	Подпись	Дата	Оценка
Студент	Терещук А.И.
Консультант	Карасев Е.М.
Проверил

Метод Симпсона (парабол)

Введение

При решении ряда актуальных физических и технических задач встречаются определенные интегралы от функций, первообразные которых не выражаются через элементарные функции. Кроме того, в приложениях приходится иметь дело с определенными интегралами, сами подынтегральные функции которых не являются элементарными. Это приводит к необходимости разработки приближенных методов вычисления определенных интегралов.

Мне была поставлена задача исследовать два метода вычисления определенных интегралов: метод трапеций и метод Симпсона (парабол)

метод трапеция симпсон интеграл

Теоретическая часть

Метод трапеций

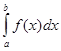
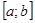
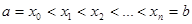
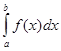
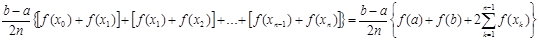
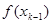
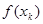
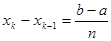
Пусть требуется вычислить интеграл . Разобьем сегмент на n равных частей при помощи точек . Метод трапеций заключается в замене интеграла суммой

площадей трапеций с основаниями, соответственно равными и , и с высотами, равными .

Таким образом, справедлива формула:

,

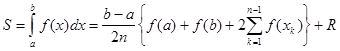
Где R — остаточный член. Это формула называется формулой трапеций .

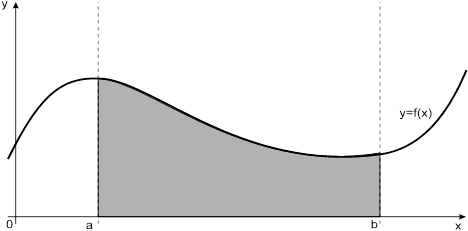
Рисунок 1 — Криволинейная трапеция

По методу трапеций интеграл равен сумме площадей прямоугольных трапеций, где основание трапеции какая-либо малая величина (точность), и сумма площадей прямоугольников, где основание прямоугольника какая-либо малая величина (точность), а высота определяется по точке пересечения верхнего основания прямоугольника, которое график функции должен пересекать в середине.

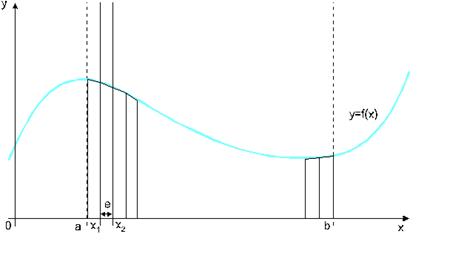
Рисунок 2 — Метод трапеций

Метод Симпсона (парабол)

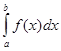
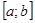
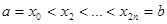
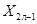
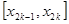
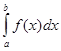
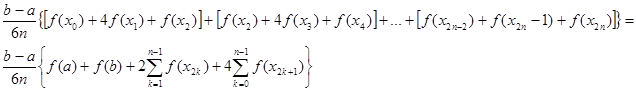
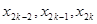
Для вычисления интеграла снова разобьем сегмент на n равных частей при помощи точек и обозначим через середину сегмента . Метод парабол заключается в замене интеграла суммой

площадей фигур и представляющий собой трапеции, лежащие под параболами, проходящими через три точки графика функции f ( x) cабсциссами .

Таким образом, справедлива формула:

,

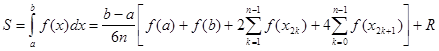
Где R — остаточный член. Это формула называется формулой Симпсона.

Пример применения

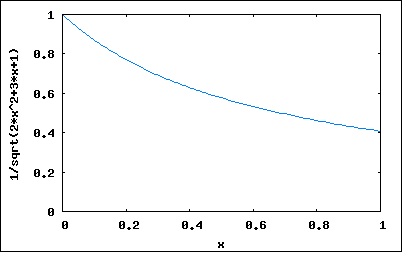
Рисунок 3 — График функции

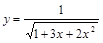	y0	y1	y2	y3	y4	y5	y6	y7	y8	y9	y10
x	0	0,1	0,2	0,3	0,4	0,5	0,6	0,7	0,8	0,9	1
y	1	0,86	0,76	0,68	0,6	0,55	0,5	0,47	0,46	0,43	0,41

Найдем площадь криволинейной трапеции методом трапеций:

S=0,1* ( (1+0,41) /2+0,86+0,76+0,68+0,6+0,55+0,5+0,47+0,46+0,43) =0,6025 кв. ед

Найдем площадь криволинейной трапеции методом Симпсона:

S=0,0017*2* (1+0,41+2* (0,76+0,6+0,5+0,46) +4* (0,86+0,68+0,55+0,47+0,43)) =

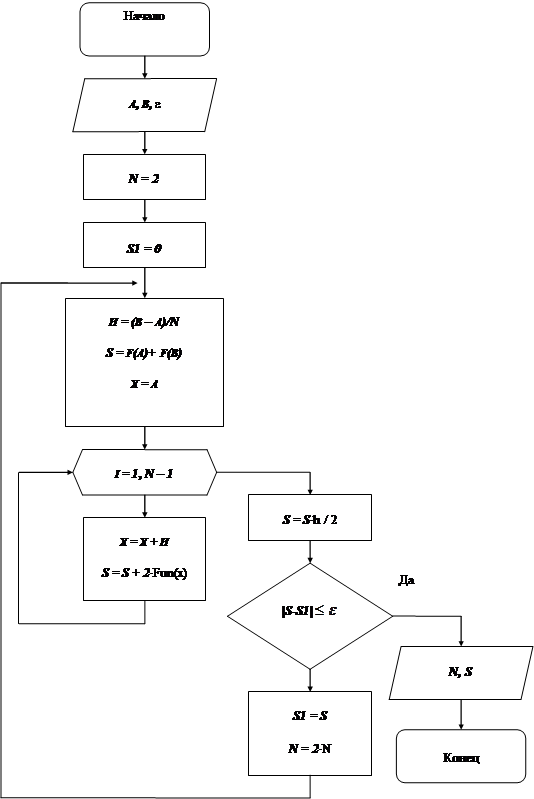Блок-схема метода трапеций

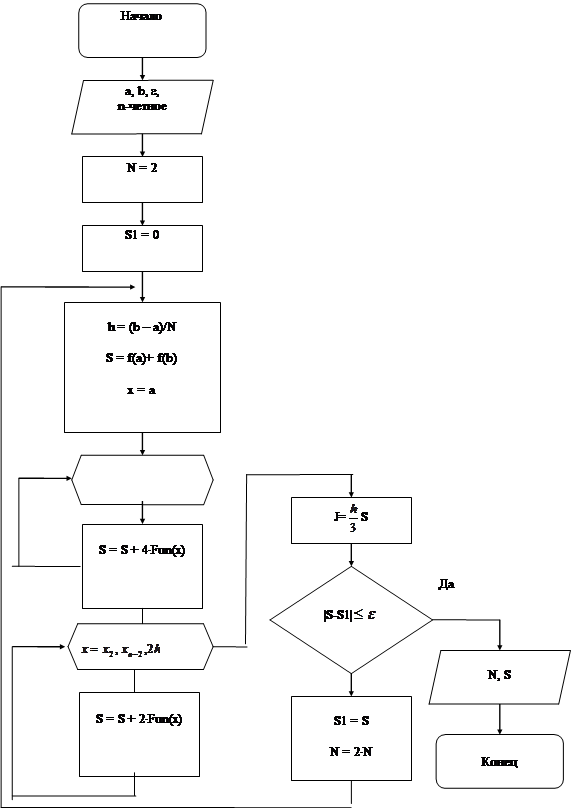Блок-схема метода Симпсона

Практическая часть

Конструирование интерфейса

Программа разрабатывается в объектно-ориентированной среде программирования Lazarus.

Перед началом программирования, была создана форма Заставка.

Рисунок 4 — Заставка

В этом окне расположены:

· Кнопка «Запуск», позволяющая приступить к началу программы;

Затем была создана основная форма Меню, позволяющая выбирать операции.

Рисунок 5 — Основная форма

Данное окно представляет главное окно программы.

В этом окне расположены:

· Компоненты Label для подписи компонентов Edit;

· Компонент MainMenuдля выбора операции;

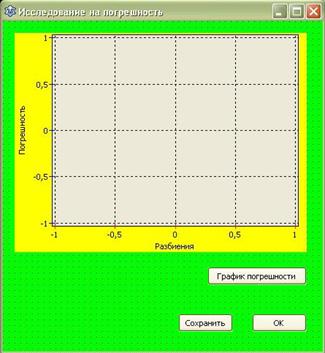
Далее была создана форма Параметры, предназначенная для введения данных.

Рисунок 6 — Параметры

В этом окне расположены:

· Компоненты Label для подписи компонентов Edit;

· Две кнопки: «OK» — принимает данные и возвращается на главное меню; «Отмена» — позволяет вернуться к главному окну, не принимая данных;

Затем была создана форма Решение, на которой будет показана площадь по разным методам вычислений и визуализироваться один из методов.

Рисунок 7 — Решение

В этом окне расположены:

· Компонент Label для подписи компонента Edit;

· Две кнопки: «График» — визуализирует метод трапеций; «OK» — принимает данные и возвращается на главное меню;

· Компонент Chartдля отображения графика;

Следующая форма была создана сравнение методов, то есть для исследования методов на погрешность с заданной точностью.

Рисунок 8 — Исследование на погрешность

В этом окне расположены:

· Три кнопки: Кнопка «График погрешности» визуализирует сравнение методов; Кнопка «Сохранить» сохраняет результаты сравнения в текстовый файл; Кнопка «OK» — принимает данные и возвращается на главное меню;

· Компонент Chartдля отображения графика;

Программное вычисление

По блок-схеме была создана программа для вычисления интеграла методами Симпсона и трапеций:

a,b,E,h,S,S1,x: real; n, i: integer;

function f (x: real): real;

// В соответствие с блок-схемой напишем программу на языке высокого уровня:

procedure TForm2. MenuItem4Click (Sender: TObject);

// найдем площадь интеграла по методу трапеций

S: =0; // изначально обнуляем значение площади интеграла

n: =1; // начальное значение количества разбиений

Repeat // начало цикла

S1: =S; // предыдущее значение площади изначально равно значению площади с количеством разбиений равным 1

n: =2*n; // увеличиваем количество разбиений в два раза

h: = (b-a) /n; // формула вычисления шага

S: =f (a) +f (b); // значение функции в нижнем пределе + значение функции в верхнем пределе определенного интеграла

x: =a; // значению xприсвоим значение нижнего предела

fori: =1 ton-1 do // для i-того элемента, изменяющегося от 1 до n-1

Источник

Вычисление интегралов

Методика и основные этапы нахождения параметров: площади криволинейной трапеции и сектора, длины дуги кривой, объема тел, площади поверхности тел вращения, работы переменной силы. Порядок и механизм вычисления интегралов с помощью пакета MathCAD.

Рубрика	Математика
Вид	контрольная работа
Язык	русский
Дата добавления	21.11.2010
Размер файла	752,3 K

Отправить свою хорошую работу в базу знаний просто. Используйте форму, расположенную ниже

Студенты, аспиранты, молодые ученые, использующие базу знаний в своей учебе и работе, будут вам очень благодарны.

Нахождение производной f’ (x) или дифференциала df=f’ (x) dx функции f(x) является основной задачей дифференциального исчисления. В интегральном исчислении решается обратная задача: по заданной функции f(x) требуется найти такую функцию F(x), что F’ (х)=f(x) или F(x)=F’ (x) dx=f(x) dx. Таким образом, основной задачей интегрального исчисления является восстановление функции F(x) по известной производной (дифференциалу) этой функции. Интегральное исчисление имеет многочисленные приложения в геометрии, механике, физике и технике. Оно дает общий метод нахождения площадей, объемов, центров тяжести и т.д.

Курс математического анализа содержит разнообразный материал, однако, одним из его центральных разделов является определенный интеграл. Интегрирование многих видов функций подчас представляет собой одну из труднейших проблем математического анализа.

Вычисление определенного интеграла имеет не только теоретический интерес. К его вычислению сводятся иногда задачи, связанные с практической деятельностью человека.

Также понятие определенного интеграла широко используется в физике.

1. Нахождение площади криволинейной трапеции

Криволинейной трапецией называется фигура, расположенная в прямоугольной системе координат и ограниченная осью абсцисс, прямыми х = а и х = b и кривой , причем неотрицательна на отрезке . Приближенно площадь криволинейной трапеции можно найти так:

1. разделить отрезок оси абсцисс на n равных отрезков;

2. провести через точки деления отрезки, перпендикулярные к оси абсцисс, до пересечения с кривой ;

3. заменить получившиеся столбики прямоугольниками с основанием и высотой, равной значению функции f в левом конце каждого отрезка;

4. найти сумму площадей этих прямоугольников.

Но можно найти площадь криволинейной иначе: по формуле Ньютона-Лейбница. Для доказательства формулы, носящей их имена, докажем, что площадь криволинейной трапеции равна , где — любая из первообразных функции , график которой ограничивает криволинейную трапецию.

Вычисление площади криволинейной трапеции записывается так:

1. находится любая из первообразных функции .

2. записывается . — это формула Ньютона-Лейбница.

2. Нахождение площади криволинейного сектора

Площадь криволинейного сектора.

Рассмотрим кривую ? = ? (?) в полярной системе координат, где ? (?) — непрерывная и неотрицательная на [?; ?] функция. Фигура, ограниченная кривой ? (?) и лучами ? = ?, ? = ?, называется криволинейным сектором. Площадь криволинейного сектора равна

3. Нахождение длины дуги кривой

Пусть в прямоугольных координатах дана плоская кривая AB, уравнение которой y = f(x), где a ? x ? b. (рис 2) [7]

Под длиной дуги AB понимается предел, к которому стремиться длина ломаной линии, вписанной в эту дугу, когда число звеньев ломаной неограниченно возрастает, а длина наибольшего звена ее стремиться к нулю.

Применим схему I (метод сумм).

Точками X = a, X, …, X = b (X ? X? … ? X) разобьем отрезок [a, b] на n частей. Пусть этим точкам соответствуют точки M = A, M, …, M = B на кривой AB. Проведем хорды MM, MM, …, MM, длины которых обозначим соответственно через ?L, ?L, …, ?L.

Получим ломанную MMM … MM, длина которой равна L = ?L+ ?L+ … + ?L = ?L.

Длину хорды (или звена ломанной) ?L можно найти по теореме Пифагора из треугольника с катетами ?X и ?Y:

?L = , где ?X = X — X, ?Y = f(X) — f(X).

По теореме Лагранжа о конечном приращении функции

?Y = (C) ?X, где C (X, X).

а длина всей ломанной MMM … MM равна

Длина кривой AB, по определению, равна

Заметим, что при ?L 0 также и ?X 0 (?L = и следовательно | ?X |

Источник