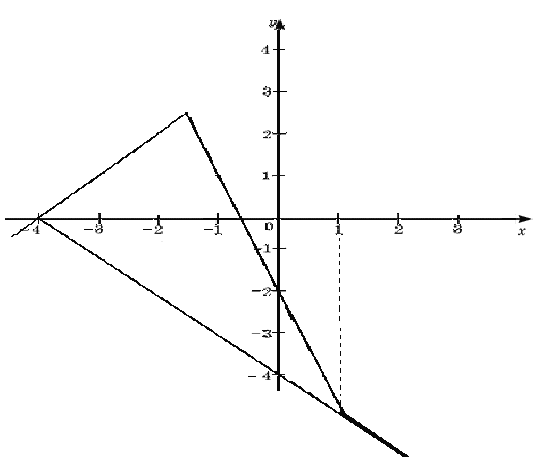
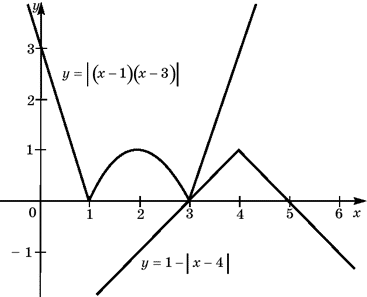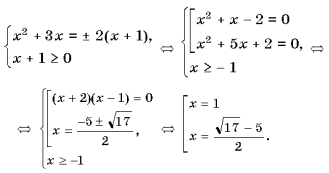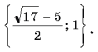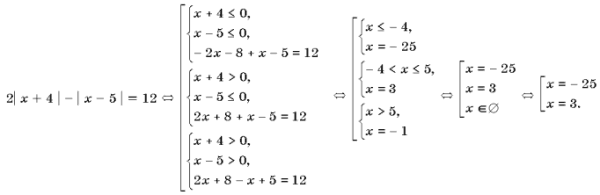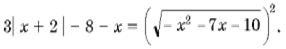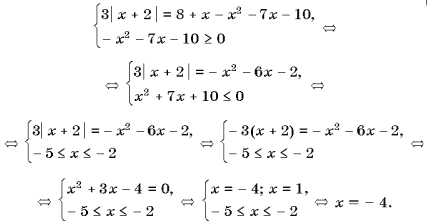Графический метод решения уравнений
Я выбрала эту тему, так как она является неотъемлемой частью изучения школьного курса алгебры. Готовя данную работу, я ставила цель более глубокого изучения этой темы, выявления наиболее рационального решения, быстро приводящего к ответу. Моя исследовательская работа поможет понять другим ученикам применение графического метода решения уравнений с параметрами, узнать о происхождении, развитии этого метода. В современной жизни изучение многих физических процессов и геометрических закономерностей часто приводит к решению задач с параметрами. Для решения таких уравнений графический метод является весьма эффективным, когда нужно установить, сколько корней имеет уравнение в зависимости от параметра α. Задачи с параметрами представляют чисто математический интерес, способствуют интеллектуальному развитию учащихся, служат хорошим материалом для отработки навыков. Они обладают диагностической ценностью, так как с помощью них можно проверить знание основных разделов математики, уровень математического и логического мышления, первоначальные навыки исследовательской деятельности и перспективные возможности успешного овладения курса математики в высших учебных заведениях. В моей работе рассмотрены часто встречающиеся типы уравнений, и, я надеюсь, что знания, полученные мной в процессе работы, помогут мне при сдаче школьных экзаменов, ведь уравнения с параметрами по праву считаются одними из самых сложных задач в курсе школьной математики. Именно такие задачи и попадают в список заданий на едином государственном экзамене ЕГЭ.
Скачать:
| Вложение | Размер |
|---|---|
| graficheskiy_metod_resheniya_uravneniy_s_parametrom.pptx | 961.23 КБ |
| graficheskiy_metod_resheniya_uravneniy.docx | 2.75 МБ |
Предварительный просмотр:
Подписи к слайдам:
Графический метод решения уравнений с параметром Автор: Назарова Алёна у ченица 11 класса « Тарбагатайской СОШ» Руководитель: Покацкая Анна Фёдоровна учитель математики
Цель работы : выявить наиболее рациональное решение, быстро приводящее к ответу. Задача: — рассмотреть теорию методов решения задач с параметрами; — разобрать поэтапно способы решения задач с параметрами на примерах; — сделать выводы по изученному материалу. Объект исследования : Уравнения с параметрами. Методы исследования: Эмпирический: формирование проблемы, гипотезы, задач, составление плана работы, оформление результатов исследовательской работы. Теоретический: анализ литературных и архивных данных, работа в Интернете
История возникновения Задачи на уравнения с параметром встречались уже в астрономическом трактате « Ариабхатиам », составленном в 499 году. Индийский учёный изложил общее правило решения квадратных уравнений, приведённых к канонической системе.
Автор насчитывает 6 видов уравнений, выражая их следующим образом: 1) «Квадраты равны корням», т. е. αx 2 = bx . 2) «Квадраты равны числу», т. е. αx 2 = c. 3) «Корни равны числу», т. е. αx = c. 4) «Квадраты и числа равны корням», т. е. αx 2 + c = bx . 5) «Квадраты и корни равны числу», т. е. αx 2 + bx = c. 6) «Корни и числа равны квадратам», т. е. bx + c = αx 2 .
Теорема Виетта (α + b ) x – x 2 = α b , Т. е. x 2 — (α – b ) x + α b =0, то x 1 = α, x 2 = b . Теорема Виетта — теорема, выражает связь между параметрами, коэффициентами квадратного уравнения и его корнями . Таким образом, Виета установил единообразие в приёмах решения уравнений.
Основные понятия Параметр — независимая переменная, значение которой считается фиксированным или произвольным числом, или числом, принадлежащим заданному условием задачи промежутку. Уравнение с параметром — математическое уравнение, внешний вид и решение которого зависит от значений одного или нескольких параметров. Системой допустимых значений переменных a ,с, k , х называется любая система значений переменных, при которой и левая и правая части этого уравнения принимают действительные значения. Равносильными уравнениями , называются два уравнения содержащие одни и те же параметры.
Методы решения уравнений с параметрами 1. Аналитический метод 2. Графический метод 3. Алгебраический метод 4. Метод симметрии 5. Решение с помощью производной
Небольшая история возникновения этого метода. Исследование общих зависимостей началось еще в 14 веке. Французский учёный Николай Орем стал изображать интенсивность длинами отрезков. Когда он располагал эти отрезки перпендикулярно некоторой прямой, их концы образовывали линию, названную им « линией интенсивности» Понятие переменный величины, ввёл французский философ и математик Рене Декарт. Также он ввёл фиксированный единичный отрезок и стал рассматривать отношение других отрезков к нему. Таким образом, графики функций за всё время прошли через фундаментальные преобразования., приведших их к тому виду, как мы привыкли.
Графический метод График функции- множество точек, у которых с абсциссы являются допустимыми значениями аргумента х , а ординаты- соответствующими значениями функции у. При графическом решении уравнения с параметром необходимо: 1.Найти область определения уравнения, т.е. область допустимых значений неизвестного и параметра, при которых уравнение может иметь решения. 2.Выразить параметр как функцию от x: 3.В системе координат хОa построить графики функций и для тех значений х , которые входят в область определения уравнения. 4.Определить точки пересечения прямой с графиком функции .
Виды уравнений с параметрами Линейное ( ax=b) Квадратное (ax^2+bx+c=0) Логарифмическое Тригонометрическое
Решение логарифмического уравнения с параматером
Заключение Таким образом, графический способ определения числа корней уравнения зависимости от входящего в него параметра, является более удобным, чем аналитический. И в заключении хотелось бы сказать, что работа над данной темой была интересной и познавательной. Изучив метод решения уравнений с параметром, я обогатила свой опыт: -Новыми понятиями -Узнала методы, которые выходят из рамки школьной программы. -Углубила и расширила свои знания. Изучив данную тему, можем сделать вывод. Параметр- это буква, которая никому ничем не обязана и может принимать любые допустимые значения .
Источник
Реферат: Графическое решение уравнений
Графическое решение уравнений
Необходимость решать квадратные уравнения еще в древности была вызвана потребностью решать задачи, связанные с нахождением площадей земельных участков и с земляными работами военного характера, а также с развитием астрономии и самой математики. Квадратные уравнения вавилоняне умели решать еще около 2000 лет до н.э. Правило решения этих уравнений, изложенное в Вавилонских текстах, совпадает по существу с современными, однако неизвестно, каким образом дошли вавилоняне до этого правила.
Формулы решения квадратных уравнений в Европе были впервые изложены в «Книге абака», написанной в 1202 году итальянским математиком Леонардо Фибоначчи. Его книга способствовала распространению алгебраических знаний не только в Италии, но и Германии, Франции и других странах Европы.
Но общее правило решения квадратных уравнений, при всевозможных комбинациях коэффициентов b и c было сформулировано в Европе лишь в 1544 году М. Штифелем.
В 1591 году Франсуа Виет ввел формулы для решения квадратных уравнений.
В древнем Вавилоне могли решить некоторые виды квадратных уравнений.
Диофант Александрийский и Евклид, Аль-Хорезми и Омар Хайям решали уравнения геометрическими и графическими способами.
В 7 классе мы изучали функции у = С, у = kx, у = kx+m, у = x2,у = – x2, в 8 классе – у = √x, у =|x|, у = ax2+bx+c, у = k/x. В учебнике алгебры 9 класса я увидела ещё не известные мне функции: у = x3, у = x4,у = x2n, у = x—2n, у = 3√x, (x– a)2 + (у – b)2 = r2 и другие. Существуют правила построения графиков данных функций. Мне стало интересно, есть ли ещё функции, подчиняющиеся этим правилам.
Моя работа заключается в исследовании графиков функций и графическом решении уравнений.
1. Какие бывают функции
График функции – это множество всех точек координатной плоскости, абсциссы которых равны значениям аргументов, а ординаты – соответствующим значениям функции.
Линейная функция задаётся уравнением у = kx+ b, гдеk и b – некоторые числа. Графиком этой функции является прямая.
Функция обратной пропорциональности у = k/x, где k ¹ 0. График этой функции называется гиперболой.
Функция (x– a)2+ (у – b)2= r2, где а, b и r – некоторые числа. Графиком этой функции является окружность радиуса r с центром в т. А (а, b).
Квадратичная функция y= ax2+ bx+ c где а, b, с – некоторые числа и а ¹ 0. Графиком этой функции является парабола.
Уравнение. График этого уравнения называется астроидой.
Функции: у = x3 – кубическая парабола, у = x4, у = 1/x2.
2. Понятие уравнения, его графического решения
Уравнение – выражение, содержащее переменную.
Решить уравнение – это значит найти все его корни, или доказать, что их нет.
Корень уравнения – это число, при подстановке которого в уравнение получается верное числовое равенство.
Решение уравнений графическим способомпозволяет найти точное или приближенное значение корней, позволяет найти количество корней уравнения.
При построении графиков и решении уравнений используются свойства функции, поэтому метод чаще называют функционально-графическим.
Для решения уравнение «делим» на две части, вводим две функции, строим их графики, находим координаты точек пересечения графиков. Абсциссы этих точек и есть корни уравнения.
3. Алгоритм построения графика функции
Зная график функции у = f(x), можно построить графики функций у = f(x+m),у = f(x)+l и у = f(x+ m)+ l. Все эти графики получаются из графика функции у = f(x) с помощью преобразования параллельного переноса: на │m│ единиц масштаба вправо или влево вдоль оси x и на │l│ единиц масштаба вверх или вниз вдоль оси y.
4. Графическое решение квадратного уравнения
На примере квадратичной функции мы рассмотрим графическое решение квадратного уравнения. Графиком квадратичной функции является парабола.
Что знали о параболе древние греки?
Современная математическая символика возникла в 16 веке.
У древнегреческих же математиков ни координатного метода, ни понятия функции не было. Тем не менее, свойства параболы были изучены ими подробно. Изобретательность античных математиков просто поражает воображение, – ведь они могли использовать только чертежи и словесные описания зависимостей.
Наиболее полно исследовал параболу, гиперболу и эллипс Аполоний Пергский, живший в 3 веке до н.э. Он же дал этим кривым названия и указал, каким условиям удовлетворяют точки, лежащие на той или иной кривой (ведь формул-то не было!).
Существует алгоритм построения параболы:
Находим координаты вершины параболы А (х0; у0): х=-b/2a;
Находим ось симметрии параболы (прямая х=х0);
Составляем таблицу значений для построения контрольных точек;
Строим полученные точки и построим точки им симметричные относительно оси симметрии.
1. По алгоритму построим параболу y= x2– 2x– 3. Абсциссы точек пересечения с осью xи есть корни квадратного уравнения x2– 2x– 3 = 0.
Существует пять способов графического решения этого уравнения.
2. Разобьём уравнение на две функции: y=x2и y= 2x+ 3. Корни уравнения – абсциссы точек пересечения параболы с прямой.
3. Разобьём уравнение на две функции: y=x2–3 и y=2x. Корни уравнения – абсциссы точек пересечения параболы с прямой.
4. Преобразуем уравнениеx2– 2x– 3 = 0 при помощи выделения полного квадрата на функции: y= (x–1)2иy=4. Корни уравнения – абсциссы точек пересечения параболы с прямой.
5. Разделим почленно обе части уравненияx2– 2x– 3 = 0 на x, получим x– 2 – 3/x= 0, разобьём данное уравнение на две функции: y= x– 2, y= 3/x. Корни уравнения – абсциссы точек пересечения прямой и гиперболы.
5. Графическое решение уравнений степени n
Корнями данного уравнения является абсцисса точки пересечения графиков двух функций: y= x5, y= 3 – 2x.
Корнями данного уравнения является абсцисса точки пересечения графиков двух функций: y= 3√x, y= 10 – x.
На примере решения квадратного уравнения можно сделать выводы, что графический способ применим и для уравнений степени n.
Графические способы решения уравнений красивы и понятны, но не дают стопроцентной гарантии решения любого уравнения. Абсциссы точек пересечения графиков могут быть приближёнными.
В 9 классе и в старших классах я буду ещё знакомиться с другими функциями. Мне интересно знать: подчиняются ли те функции правилам параллельного переноса при построении их графиков.
На следующий год мне хочется также рассмотреть вопросы графического решения систем уравнений и неравенств.
1. Алгебра. 7 класс. Ч. 1. Учебник для общеобразовательных учреждений/ А.Г. Мордкович. М.: Мнемозина, 2007.
2. Алгебра. 8 класс. Ч. 1. Учебник для общеобразовательных учреждений/ А.Г. Мордкович. М.: Мнемозина, 2007.
3. Алгебра. 9 класс. Ч. 1. Учебник для общеобразовательных учреждений/ А.Г. Мордкович. М.: Мнемозина, 2007.
4. Глейзер Г.И. История математики в школе. VII–VIII классы. – М.: Просвещение, 1982.
5. Журнал Математика №5 2009; №8 2007; №23 2008.
Источник
Реферат: Алгебраическое и графическое решение уравнений, содержащих модули
| Название: Алгебраическое и графическое решение уравнений, содержащих модули Раздел: Рефераты по математике Тип: реферат Добавлен 22:53:07 24 марта 2007 Похожие работы Просмотров: 11201 Комментариев: 33 Оценило: 29 человек Средний балл: 4.6 Оценка: 5 Скачать |


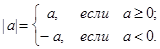
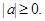
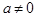 равна большему из двух чисел a или -a.
равна большему из двух чисел a или -a.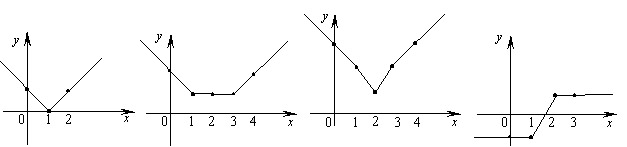
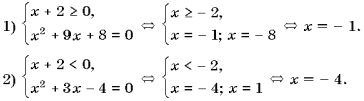
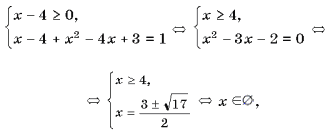 так как
так как