Развертка призмы способ нормального сечения

Развертка поверхности призмы

Существует два способа развертки призмы: способ «нормального сечения» и способ «раскатки».

Способ «нормального сечения» используют для развертки поверхности призм общего положения. В этом случае строится нормальное сечение призмы (т.е. вводится плоскость, расположенная перпендикулярно боковым ребрам призмы) и определяются натуральные величины сторон многоугольника этого нормального сечения.

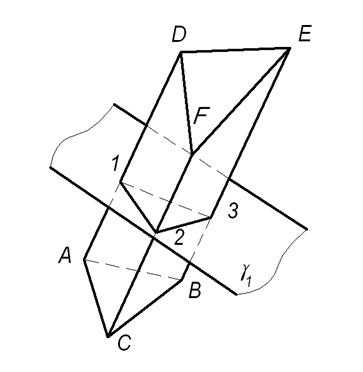
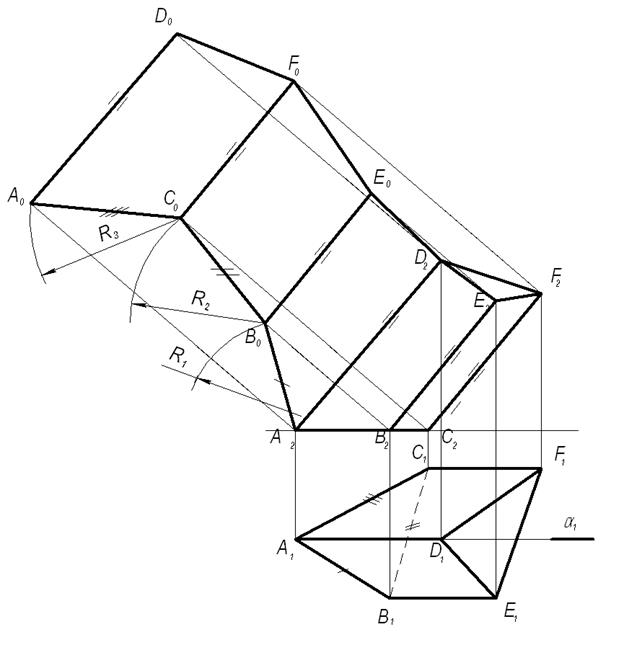
Пример выполнения развертки трехгранной призмы общего положения способом «нормального сечения» рассмотрим в задаче согласно рисунка 1.5.1

Обратим внимание на то, что в нашем случае боковые ребра призмы являются фронталями, т.е. на плоскость П₂ они проецируются в натуральную величину.

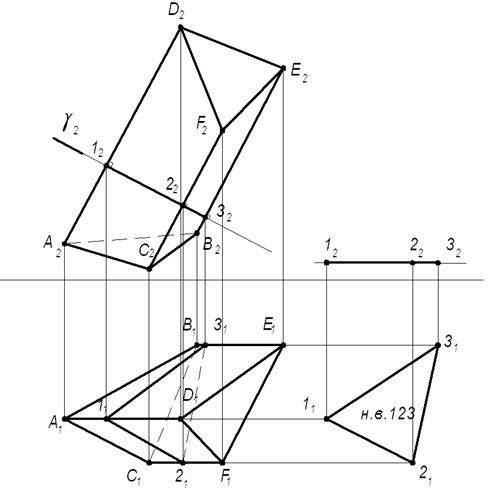
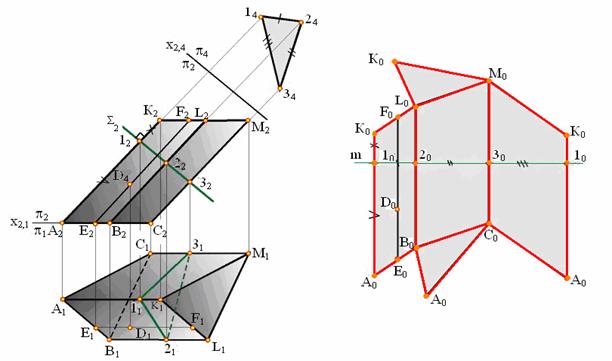
1) Во фронтальной плоскости проекций построим фронтально проецирующую плоскость γ(γ₁), которая одновременно перпендикулярна боковым ребрам призмы AD, CF, BE. Полученное нормальное сечение выразится в виде треугольника 123. Методом плоско-параллельного перемещения определим его натуральную величину в соответствии с рисунком 1.5.2.

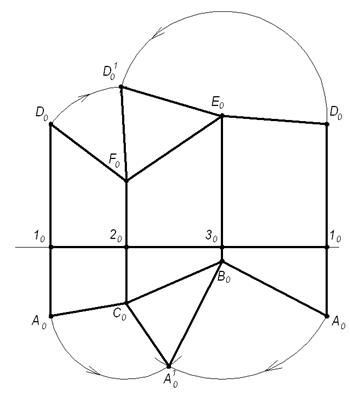
4) Полученные точки верхнего и нижнего оснований призмы соединим прямыми A₀B₀C₀ и D₀F₀E₀. Плоская фигура A₀B₀C₀D₀F₀E₀ является искомой разверткой боковой поверхности данной призмы. Для построения полной развертки необходимо к развертке боковой поверхности пристроить натуральные величины оснований. Для этого воспользуемся полученными на развертке натуральными величинами их сторон A₀C₀, C₀B₀, B₀A₀ и D₀F₀, F₀E₀, E₀D₀ в соответствии с рисунком 1.5.3

Рисунок 1.5.3 – Развертка призмы способом «нормального сечения»

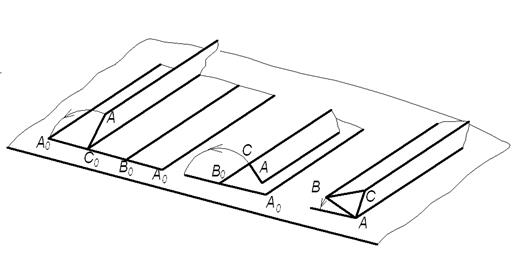
Способ «раскатки». Этот способ удобен для построения разверток призм с основанием, лежащим в плоскости уровня. Суть способа заключается в последовательном совмещением боковых граней с плоскостью чертежа путем поворота их вокруг соответствующих ребер призмы (рисунок 1.5.4).

Этим способом построена развертка поверхности призмы ABCDEF , боковые ребра которой являются фронталями, а нижнее основание лежит в горизонтальной плоскости (рисунок 1.5.5).

1) Боковые грани призмы совместим с фронтальной плоскостью, проходящей через ребро AD. Это удобно в этом случае, т.к. фронтальные проекции боковых ребер призмы равны их истинной длине. Тогда ребро A₀D₀ развертки будет совпадать с фронтальной проекцией ребра AD(A₂D₂).

2) Для определения на развертке истиной величины боковой грани ADEB вращаем ее вокруг ребра AD до положения, параллельного фронтальной плоскости проекций. Чтобы определить на развертке положение точки B₀, из точки B₂ восстанавливаем перпендикуляр к A₂D₂. Точка B₀ будет найдена в пересечении этого перпендикуляра с дугой окружности радиуса R₁, равного истиной величине ребра AB и проведенной из точки A₂, как из центра.

3) Точка E₀ будет определяться на развертке как результат пересечения прямой B₀E₀ параллельной фронтальной проекцией ребра BE(B₂E₂), и перпендикуляра, восстановленного из точки E₂ к A₂D₂.

4) Точки C₀ и A₀ построены аналогично точке B₀ в пересечении перпендикуляров из точек C₂ и A₂ к фронтальным проекциям ребер, с дугами окружностей, проведенных из точек B₀ и C₀ как из центров радиусами R₂ и R₃, равными соответственно ребрам BC и CA. Точки F₀ и D₀ определяются аналогично точке E₀.

5) Соединив последовательно совмещенные вершины ломаными линиями, получим развертку боковой поверхности призмы A₀B₀C₀A₀D₀F₀E₀D₀. При необходимости можно получить полную развертку призмы, присоединив к ней натуральные величины обоих оснований.

Если боковые ребра призмы занимают общее положение, то предварительным преобразованием чертежа их надо привести в положение линий уровня.

Рисунок 1.5.4 – Способ «раскатки»

Рисунок 1.5.5 – Развертка боковой поверхности призмы способом «раскатки»

Источник

Способ нормального сечения

Под разверткой многогранной поверхности подразумевают плоскую фигуру, составленную из граней этой поверхности, совмещенных с одной плоскостью. Так как все грани многогранника изображаются на развертке в натуральную величину, построение развертки сводится к определению натуральной величины граней – плоских многоугольников.

Способ нормального сечения применяется для развертки призматических гранных поверхностей. Отличительная особенность данного способа является построение сечения призмы плоскостью нормальной (перпендикулярной) по отношению к ее боковым ребрам. При последующем развертывании призмы линия нормального сечения выстраивается в прямую линию и используется для откладывания от нее натуральной величины отрезков боковых ребер.

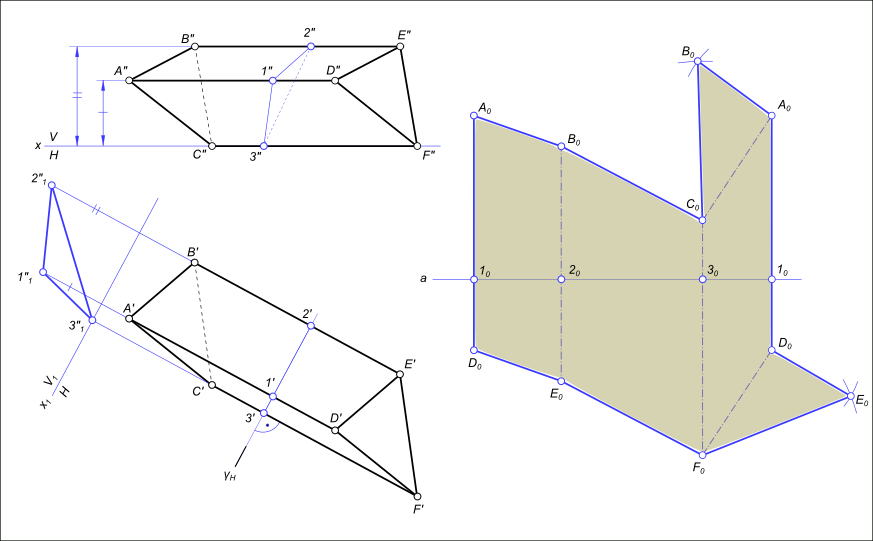
Построить развертку наклонной трехгранной призмы ABCDEF, иcпользуя способ нормального сечения.

Построим сечение заданной призмы вспомогательной плоскостью γ_H перпендикулярной к ее боковым ребрам и горизонтальной плоскости проекций H. Методом перемены плоскостей проекций определяем действительную величину сторон Δ123. В произвольном месте эпюра проводим горизонтально прямую a. От точки 1₀, отмеченной на этой прямой, откладываем отрезки [1₀2₀], [2₀3₀], [3₀1₀], конгруентные сторонам Δ123. Через точки 1₀2₀3₀ и 1₀ проводим прямые перпендикулярные к прямой a, и откладываем на них от точек 1₀2₀3₀ и 1₀ отрезки, конгруентные соответствующим действительным величинам отрезков боковых ребер. Полученные точки A₀B₀C₀A и D₀E₀ F₀D₀ соединяем прямыми. Ребра AD, BE, и CF параллельны плоскости H, поэтому на нее они проецируются в действительную величину. Плоская фигура A₀B₀C₀A₀D₀E₀F₀D₀ — развертка боковой поверхности призмы. К ней пристроены основания призмы ΔA₀B₀C₀ и ΔD₀E₀F₀.

Способ нормального сечения применяется также для получения развертки цилиндрической поверхности: Развертка цилиндра

Источник

Способ нормального сечения

Этот способ применяется для построения разверток призматических и цилиндрических поверхностей.

Построение сводится к многократному построению натурального вида трапеций, из которых состоит данная призматическая поверхность, или призматическая поверхность, вписанная (или описанная) в данную цилиндрическую поверхность и заменяющая ее. Если, в частности, призматическая или цилиндрическая поверхности ограничены параллельными основаниями, то трапеции, на которые разбивается поверхность, обращаются в прямоугольники или параллелограммы, в зависимости от того, перпендикулярны или нет плоскости оснований боковым ребрам или образующим поверхности.

Построение трапеций или параллелограммов проще всего произвести по их основаниям и высотам, причем необходимо также знать отрезки оснований, на которые они делятся высотой. Поэтому для построения развертки призматической или цилиндрической поверхности необходимо предварительно определить натуральный вид нормального сечения данной поверхности. Стороны этого сечения и будут высотами трапеций или параллелограммов, из которых состоит поверхность. Этот способ называется СПОСОБОМ НОРМАЛЬНОГО СЕЧЕНИЯ.

Пример. Построить развертку поверхности треугольной наклонной призмы АВСDEF (рис. 167).

Боковые ребра призмы имеют горизонтальное расположение. Пересечем данную призму плоскостью a(a_H), перпендикулярной к боковым ребрам, и построим проекции фигуры сечения — треугольник 1-2-3 (рис. 167).

Определим натуральные величины сторон треугольника 1-2-3 способом замены плоскостей проекций: меняем фронтальную плоскость проекций V на новую V₁ таким образом, чтобы плоскость a стала плоскостью уровня, для чего ось x₁ новой системы плоскостей проекций H/V₁ проводим параллельно a_H. Тогда на новой фронтальной плоскости V₁ получим натуральную величину треугольника 1-2-3 (рис. 167).

На произвольной горизонтальной прямой построим отрезок, равный периметру треугольника 1-2-3 (рис. 167). Отрезок 1-1 можно считать разверткой нормального сечения призмы. Из всех точек (1,2,3,1) этого отрезка проводим прямые, перпендикулярные к нему, на которых откладываем отрезки боковых ребер (натуральные величины), беря их с горизонтальной проекции, так как они являются горизонталями. Концы отложенных отрезков соединяем прямыми СА, АВ, FD, . Фигура CABCFEDF представляет собой развертку боковой поверхности призмы.

Полная развертка призмы показана на рис. 167. Для построения граней основания из точек В и С проводим дуги окружностей радиусами, равными соответственно натуральным величинам ребер ВА и СА. Пересечение дуг дает точку А. Аналогичным образом найдена точка D.

Способ раскатки

Способ раскатки рекомендуется для построения развертки цилиндрической поверхности, когда ее образующие являются прямыми уровня, то есть параллельными одной из плоскостей проекций.

Рассмотрим данный способ на примере эллиптического цилиндра с круговым основанием, которое проецируется на горизонтальную плоскость проекций без искажения (в натуральную величину).

Построение развертки данного цилиндра выполняем в следующей последовательности (рис. 168):

1. Делим окружность основания цилиндра на 12 равных частей.

2. Вписываем в цилиндр призму, боковые ребра которой совпадают с образующими цилиндра, проходящими через точки деления основания (рис. ).

3. Принимаем за плоскость развертки фронтальную плоскость g (g_H), которая проходит через ребро призмы, совпадающее с очерковой образующей цилиндра (1).

4. Находим натуральную величину первой грани, проходящей через ребро 1, для чего вращаем ее вокруг фронтали 1”до уровня этой фронтали. При этом точка 2”переместится по направлению, перпендикулярному к этой фронтали в положение 2, которое найдем, если из точки 1”это направление засечем отрезком 1’2′.

Из точки 3”проводим также перпендикуляр к ребру 1(1”) и находим точку 3, отсекая этот перпендикуляр из точки 2 отрезком 2’3′ и т.д.

Соединяя найденные точки плавной кривой получим фигуру развертки, которую можно представлять себе как отпечаток цилиндра, полученный путем его качения по фронтальной плоскости, проходящей через образующую 1.

Источник

Построение развертки призмы способом нормального сечения

Построение развертки пирамиды способом триангуляции

Боковые грани любой пирамиды являются треугольниками. Для построения развертки пирамиды (рис. 9.2) необходимо предварительно определить натуральные величины боковых ребер и сторон основания.

.

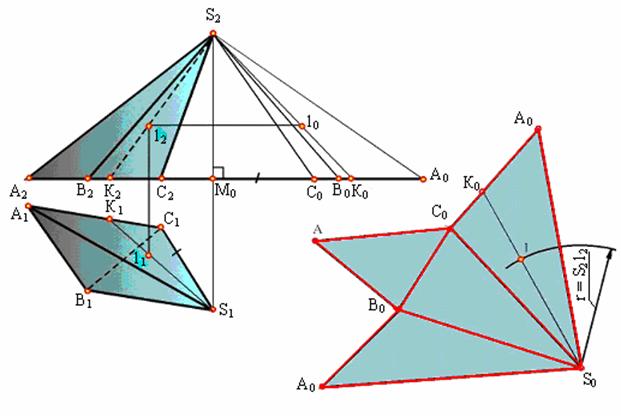
Рис. 9.2. Построение развертки пирамиды

Следующая операция состоит в построении каждой боковой грани как треугольника по трем сторонам. В результате получается развертка боковой поверхности пирамиды в виде ряда примыкающих друг к другу треугольников с общей вершиной S. Присоединив к полученной фигуре основание ( 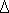АВС), получим полную развертку пирамиды. Такой способ построения развертки поверхности называется способом триангуляций.

Построение развертки призмы способом нормального сечения

Для построения развертки наклонной призмы, изображенной на рис. 9.3 необходимо найти истинные величины боковых ребер и сторон основания призмы. Призма расположена так, что ее боковые ребра параллельны плоскости П₂ и проецируются на нее в натуральную величину. Стороны оснований являются горизонталями и проецируются на плоскость П₁ без искажения. Таким образом, длины сторон каждой грани известны, однако этого еще недостаточно для построения истинной формы боковых граней.

.

Источник