Разные способы найти площадь ромба

Площадь ромба

Площадь ромба, формулы и калькулятор для вычисления площади в режиме онлайн.

Для вычисления площади ромба применяются различные формулы, в зависимости от известных исходных данных. Ниже приведены формулы и калькулятор для вычисления площади ромба в режиме онлайн.

Площадь ромба по стороне и высоте

Площадь ромба по двум диагоналям

Площадь ромба по углу и противолежащей диагонали

Площадь ромба по углу и диагонали проведенной из этого угла

Площадь ромба по стороне и углу между сторонами

Площадь ромба по радиусу вписанной окружности и углу между сторонами

Площадь ромба по радиусу вписанной окружности и стороне

Если в исходных данных угол задан в радианах, то для перевода в градусы вы можете воспользоваться «Конвертером величин». Или вычислить самостоятельно по формуле: 1 рад × (180/π) ° = 57,296°

Таблица с формулами площади ромба

В зависимости от известных исходных данных, площадь ромба можно вычислить по различным формулам.

исходные данные (активная ссылка для перехода к калькулятору)	эскиз	формула
1	сторона и высота
2	диагонали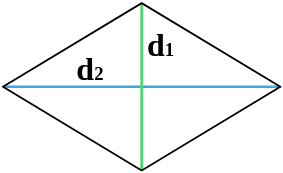
3	диагональ и угол между сторонами
4	диагональ и угол между сторонами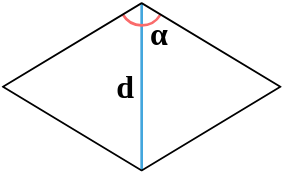
5	сторона и угол между сторонами
6	радиус вписанной окружности и угол между сторонами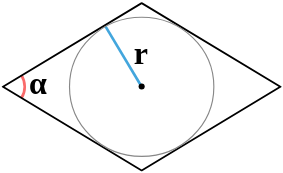
7	сторона и радиус вписанной окружности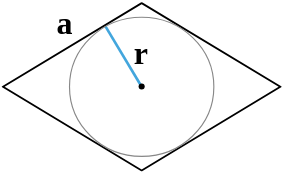

Определения

Ромб — это геометрическая фигура, образованная четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.

Ромб – это частный случай параллелограмма.

Высота ромба – это отрезок проведенный из вершины ромба к противоположной стороне под углом в 90 градусов.

Площадь – это численная характеристика, характеризующая размер плоскости, ограниченной замкнутой геометрической фигурой.

Площадь измеряется в единицах измерения в квадрате: км 2 , м 2 , см 2 , мм 2 и т.д.

Площадь ромба – это численная характеристика, характеризующая размер плоскости, ограниченной четырьмя последовательно соединенными отрезками (сторонами) одинаковой длины, у которой противоположные стороны попарно параллельны, а угол между любыми двумя смежными сторонами не равен 90 градусов.

Источник

Площади фигур. Площадь ромба.

Площадь плоской фигуры — аддитивная числовая характеристика фигуры, полностью принадлежащей

одной плоскости. Если фигуру можно разбить на конечное множество единичных квадратов, то площадь

будет равна числу этих квадратов.

Ромб — это параллелограмм с равными сторонами. Ромб с прямыми углами называется квадратом.

Площадь ромба равна половине произведения его диагоналей.

Воспользуйтесь нашим калькулятором для расчета площади ромба.

Для расчета площади других фигур воспользуйтесь этим калькулятором: площади фигур.

Формулы для вычисления площади ромба.

1. Формула площади ромба по длине стороны и его высоте.

Площадь ромба равна произведению длины его стороны и длины опущенной на эту сторону высоты.

1. Формула площади ромба по длине стороны и углу.

Площадь ромба равна произведению квадрата длины его стороны и синуса угла между сторонами ромба.

1. Формула площади ромба по длинам его диагоналей.

Площадь ромба равна половине произведению длин его диагоналей.

где S — Площадь ромба,

a — длина стороны ромба,

h — длина высоты ромба,

α — угол между сторонами ромба,

d₁, d₂ — длины диагоналей.

Еще некоторые формулы для определения площади ромба:

Источник

Площадь ромба онлайн

С помощю этого онлайн калькулятора ромба можно найти площадь ромба по известным элементам. Для нахождения площади ромба введите известные данные в ячейки и нажмите на кнопку «Вычислить». Теоретическую часть смотрите ниже.

Открыть онлайн калькулятор

1. Площадь ромба через сторону и угол

Пусть задан ромб ABCD (Рис.1). Выведем формулу вычисления площади ромба через сторону и угол.

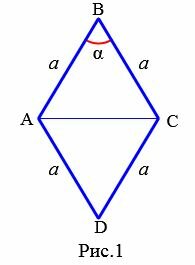Проведем диагональ AC. Тогда ромб делится на два треугольника ABC и ADC. Противолежащие углы ромба равны (свойство 1 статя Ромб). Поэтому треугольники ABC и ADC равны по двум сторонам и углу между ними. Площадь треугольника ABC по двум сторонам и углу между ними вычисляется по формуле:

\(\small S=AB \cdot BC \cdot \sin \alpha \)

или, учитывая, что AB=BC=a:

\(\small S_=\frac <\large 1><\large 2>a^2 \cdot \sin \alpha .\)

Аналогично, площадь треугольника ADC вычисляется по формуле

\(\small S_= \frac <\large 1><\large 2>a^2 \cdot \sin \alpha .\)

Поэтому площадь ромба равна:

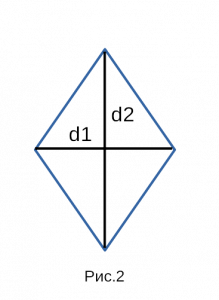
2. Площадь ромба через диагонали

Пусть известны диагонали d₁ и d₂ ромба ABCD (Рис.2). Выведем формулу вычисления площади ромба через диагонали.

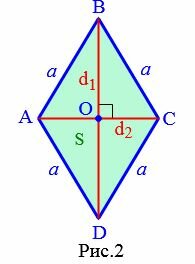Поскольку диагонали ромба перепендикулярны и точкой пересечения делятся пополам (свойства 6 и 5 ромба), то они разделяют ромб на четыре прямоугольных треугольника. Тогда эти прямоугольные треугольники равны по двум катетам: \( \small \frac <2>\) и \( \small \frac <2>\).

\(\small S_=\frac<\large 1> <\large 2>\cdot \frac<\large d_1> <\large 2>\cdot \frac<\large d_2><\large 2>\) \(\small =\frac<\large d_1 \cdot d_2> <\large 8>.\)

Тогда площадь ромба равна:

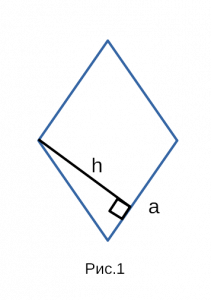
3. Площадь ромба через сторону и высоту

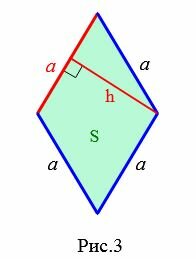Пусть известны сторона a и высота h ромба (Рис.3). Так как ромб является параллелограммом, то площадь ромба вычисляется по формуле площади параллелограмма:

4. Площадь ромба через угол и противолежащую диагональ

Пусть известны один из углов α=∠ABC ромба и противолежащий диагональ d=AC (Рис.4). Выведем формулу вычисления площади ромба.

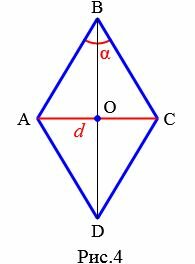Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:

\(\small S_= \frac<\large 1 > <\large 2>\cdot AO \cdot OB .\)

(3)

\(\small \frac<\large OB > <\large AO>= \mathrm \ \angle ABO \) \(\small = \mathrm \ \frac<\large \alpha> <\large 2>\)

\(\small OB= AO \cdot \mathrm \ \frac<\large \alpha> <\large 2>.\)

(4)

Подставим (4) в (3):

\(\small S_= \frac<\large 1 > <\large 2>\cdot AO \cdot AO \cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:

\(\small S_= \frac<\large d^2 > <\large 8>\cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

(5)

Тогда площадь ромба равна:

\(\small S= 4 \cdot S_=\frac<\large d^2 > <\large 2>\cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

(6)

5. Площадь ромба через угол и диагональ из данного угла

Пусть известны один из углов α=∠BAD ромба и диагональ из данного угла d=AC (Рис.5). Выведем формулу вычисления площади ромба.

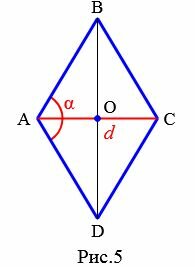Проведем другой диагональ BD. Как было отмечено в параграфе 2, диагонали ромба разделяют его на четыре равных прямоугольных треугольников. Найдем площадь одного из них:

\(\small S_= \frac<\large 1 > <\large 2>\cdot AO \cdot OB .\)

(7)

\(\small \frac<\large OB > <\large AO>= \mathrm \ \angle BAO \) \(\small = \mathrm \ \frac<\large \alpha> <\large 2>\)

\(\small OB= AO \cdot \mathrm \ \frac<\large \alpha> <\large 2>.\)

(8)

Подставим (8) в (7):

\(\small S_= \frac<\large 1 > <\large 2>\cdot AO \cdot AO \cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

или, учитывая что \( \small AO=\frac<\large d><\large 2>,\) получим:

\(\small S_= \frac<\large d^2 > <\large 8>\cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

(9)

Тогда площадь ромба равна:

\(\small S= 4 \cdot S_=\frac<\large d^2 > <\large 2>\cdot \mathrm \ \frac<\large \alpha><\large 2>.\)

(10)

6. Площадь ромба через угол и радиус вписанной в ромб окружности

Пусть известны один из углов α=∠ABC ромба и радиус r вписанной в ромб окружности (Рис.6). Выведем формулу вычисления площади ромба.

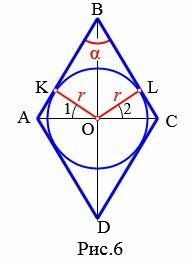Как мы отметили выше, диагонали разделяют ромб на четыре равных прямоугольных треугольника. В частности

Тогда \( \small \angle BAO=\angle BCO=90°-\frac< \large \alpha > <\large 2>\). Треугольники AKO и CLO также прямоугольные. Следовательно

\( \small \angle 1=90°- \angle BAO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>, \)

(12)

\( \small \angle 2=90°- \angle BCO \) \( \small =90°- (90°-\frac< \large \alpha ><\large 2>) \) \( \small =\frac< \large \alpha ><\large 2>. \)

(13)

Применим теорему синусов для прямоугольного треугольника AOB:

\( \small \frac<\large AO><\large \sin \frac< \alpha ><2>>= \frac<\large OB><\large \sin \left( 90°-\frac< \alpha > < 2>\right) >\) \( \small =\frac<\large OB><\large \cos \frac< \alpha > < 2>> \)

Для прямоугольного треугольника AKO имеем:

или, учитывая (12) и KO=r:

Подставляя (15) в (14), получим:

Найдем площадь треугольника AOB:

\( \small S_=\frac<\large 1 > <\large 2>\cdot AO \cdot OB\)

(17)

Подставляя (15) и (16) в (17), получим:

\( \small S_=\frac<\large 1 > <\large 2>\cdot \frac<\large r><\large \cos \frac< \alpha ><2>> \cdot \frac<\large r ><\large \sin \frac< \alpha ><2>>\) \( \small =\frac<\large r^2><\large \sin \alpha>.\)

Тогда площадь ромба равна:

7. Площадь ромба через сторону и радиус вписанной в ромб окружности

Пусть известны сторона a=AB ромба и радиус r вписанной в ромб окружности (Рис.7). Найдем площадь ромба.

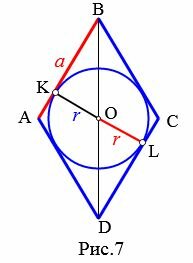Прямая AB является касательной к окружности вписанной в ромб. Тогда \( \small OK ⊥ AB \). Прямая CD является касательной к окружности вписанной в ромб. Тогда \( \small OL ⊥ CD \). Поэтому треугольники BKO и DLO прямоугольные. Эти треугольники равны по гипотенузе и катету (BO=OD, KO=OL). Тогда \( \small \angle BOK=\angle DOL \). Углы BOK и KOD смежные. Следовательно \( \small \angle KOD=180°-\angle BOK. \) \( \small \angle KOD+\angle DOL \) \( \small =180°-\angle BOK+\angle DOL=180°. \) Получили, что отрезки KO и OL находятся на одной прямой. То есть KL=KO+OL=2r. Поскольку \( \small KL ⊥ AB, \) то является высотой ромба. Площадь ромба по стороне и высоте вычисляется из формулы (3). Тогда имеем:

Источник

Как найти площадь ромба

Площадь ромба можно вычислить разными способами.
Например, через половину произведения двух диагоналей
друг на друга, через синус и сторону в квадрате…

Также, площадь ромба равна площади параллелограмма.

Как следствие, так, как ромб является параллелограммом, с
равными сторонами, поэтому площадь ромба
можно найти через площадь параллелограмма.

Для ромба истинны и верны все свойства параллелограмма.
Формула площади ромба и формула
площади параллелограмма одинаковая.

Ромб — параллелограмм, у которого
все четыре стороны равны.

Формулировка площади ромба через параллелограмм:

Формула площади ромба через параллелограмм:

a — основание; h — высота;

Площадь ромба, можно также найти другим способом. Для
этого мысленно разделим ромба на четыре треугольника,
так чтобы каждая вершина была соединена с противоположной
вершиной. Получившиеся линии называют диагоналями. Если
известны длины двух диагоналей ромба, то можно найти площадь.

Формула площади ромба через две диагонали:

\( S = \frac<1>2d_1 d_2 \)

d1 и d2 — диагонали;

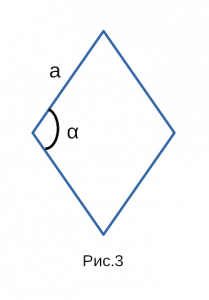
В самых редких случаях, если известен синус и одна из сторон,
используют формулу площади ромба через синус и квадрат стороны.

Формулировка площади ромба через синус и сторону в квадрате:

Формула площади ромба через синус и сторону в квадрате:

a — сторона; sin α — синус угла;

Рис. 1 — площадь ромба через площадь параллелограмма / основание и высоту.
Рис. 2 — площадь ромба через две диагонали
Рис. 3 — площадь ромба через синус и сторону в квадрате

Также, вы можете прочитать про свойства и признаки ромба.

Источник