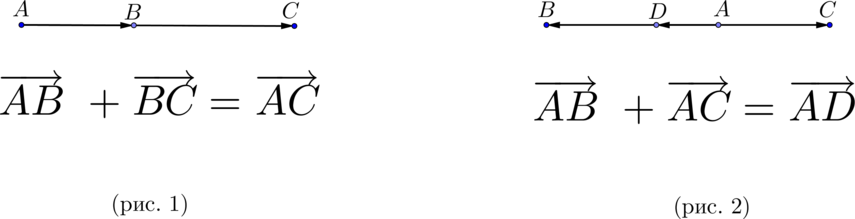Разность неколлинеарных векторов двумя способами

Содержание

Векторы: правила сложения и вычитания
Вычитание векторов. Как найти разность векторов
Откладывание вектора от данной точки
Вычитание векторов. Правило первое
Готовые работы на аналогичную тему
Вычитание векторов. Правило второе
Пример задачи на понятие разности векторов
Сложение и вычитание векторов
Формулы сложения и вычитания векторов
Формулы сложения и вычитания векторов для плоских задач
Формулы сложения и вычитания векторов для пространчтвенных задач
Формулы сложения и вычитания n -мерных векторов
Примеры задач на сложение и вычитание векторов
Примеры плоских задач на сложение и вычитание векторов
Примеры пространственных задач на сложение и вычитание векторов
Примеры задач на сложение и вычитание векторов с размерностью большей 3
Геометрия, 9 класс, урок: «Вычитание векторов»

Векторы: правила сложения и вычитания

Вектор $\overrightarrow$ можно рассматривать как перемещение точки из положения $A$ (начало движения) в положение $B$ (конец движения). То есть траектория движения в этом случае не важна, важны только начало и конец!

$\blacktriangleright$ Два вектора коллинеарны, если они лежат на одной прямой или на двух параллельных прямых.
В противном случае векторы называются неколлинеарными.

$\blacktriangleright$ Два коллинеарных вектора называются сонаправленными, если их направления совпадают.
Если их направления противоположны, то они называются противоположно направленными.

Правила сложения коллинеарных векторов:

$\blacktriangleright$ Для того, чтобы сложить два сонаправленных вектора, можно отложить второй вектор от конца первого. Тогда их сумма – вектор, начало которого совпадает с началом первого вектора, а конец – с концом второго (рис. 1).

$\blacktriangleright$ Для того, чтобы сложить два противоположно направленных вектора, можно отложить второй вектор от начала первого. Тогда их сумма – вектор, начало которого совпадает с началом обоих векторов, длина равна разности длин векторов, направление совпадает с направлением большего по длине вектора (рис. 2).

Правила сложения неколлинеарных векторов $\overrightarrow $ и $\overrightarrow$ :

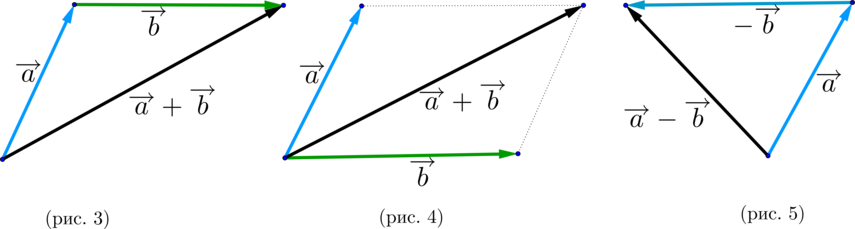
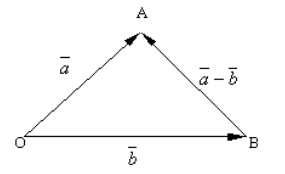
$\blacktriangleright$ Правило треугольника (рис. 3).

$\blacktriangleright$ Правило параллелограмма (рис. 4).

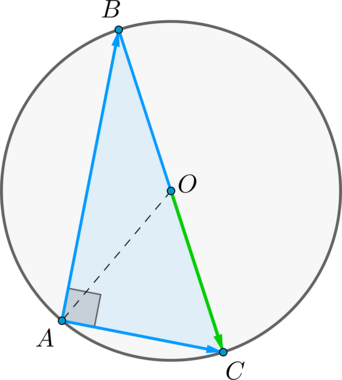
Дан прямоугольный треугольник $ABC$ с прямым углом $A$ , точка $O$ – центр описанной около данного треугольника окружности. Координаты вектора $\overrightarrow=\<1;1\>$ , $\overrightarrow=\<-1;1\>$ . Найдите сумму координат вектора $\overrightarrow$ .

Т.к. треугольник $ABC$ — прямоугольный, то центр описанной окружности лежит на середине гипотенузы, т.е. $O$ — середина $BC$ .

Заметим, что $\overrightarrow=\overrightarrow-\overrightarrow$ , следовательно, $\overrightarrow=\<-1-1;1-1\>=\<-2;0\>$ .

Т.к. $\overrightarrow=\dfrac12 \overrightarrow$ , то $\overrightarrow=\<-1;0\>$ .

Значит, сумма координат вектора $\overrightarrow$ равна $-1+0=-1$ .

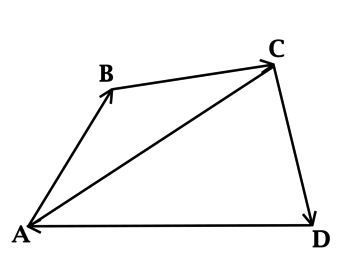
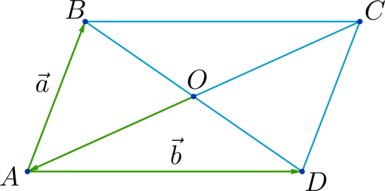
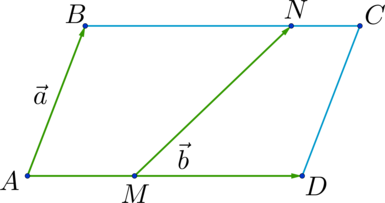
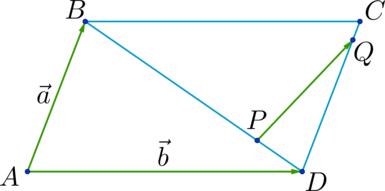
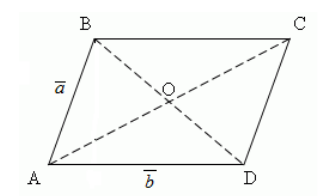
$ABCD$ – четырёхугольник, на сторонах которого отложены векторы $\overrightarrow$ , $\overrightarrow$ , $\overrightarrow$ , $\overrightarrow$ . Найдите длину вектора $\overrightarrow + \overrightarrow + \overrightarrow + \overrightarrow$ .

$\overrightarrow + \overrightarrow = \overrightarrow$ , $\overrightarrow + \overrightarrow = \overrightarrow$ , тогда
$\overrightarrow + \overrightarrow + \overrightarrow + \overrightarrow = \overrightarrow + \overrightarrow + \overrightarrow= \overrightarrow + \overrightarrow = \overrightarrow — \overrightarrow = \vec<0>$ .
Нулевой вектор имеет длину, равную $0$ .

Вектор можно воспринимать как перемещение, тогда $\overrightarrow + \overrightarrow$ – перемещение из $A$ в $B$ , а затем из $B$ в $C$ – в итоге это перемещение из $A$ в $C$ .

Читайте также: Гидравлический способ добычи золота
При такой трактовке становится очевидным, что $\overrightarrow + \overrightarrow + \overrightarrow + \overrightarrow = \vec<0>$ , ведь в итоге здесь из точки $A$ переместились в точку $A$ , то есть длина такого перемещения равна $0$ , значит, и сам вектор такого перемещения есть $\vec<0>$ .

\[\begin \overrightarrow = \overrightarrow + \overrightarrow = \frac<1><5>\overrightarrow + \frac<9><10>\overrightarrow = \frac<1><5>(\overrightarrow + \overrightarrow) + \frac<9><10>\overrightarrow =\\ = \frac<1><5>(\overrightarrow + \overrightarrow) + \frac<9><10>\overrightarrow = \frac<1><5>(\overrightarrow — \overrightarrow) + \frac<9><10>\overrightarrow = \frac<1><5>\overrightarrow + \frac<7><10>\overrightarrow = \frac<1><5>\vec + \frac<7><10>\vec\end\]

$\Rightarrow$ $x = \frac<7><10>$ , $y = \frac<1><5>$ $\Rightarrow$ $x\cdot y = 0,14$ .

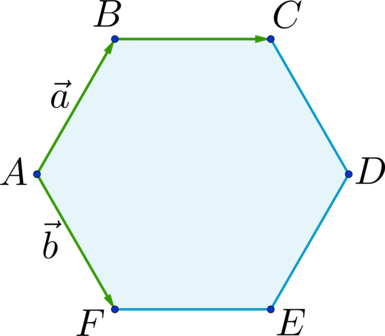
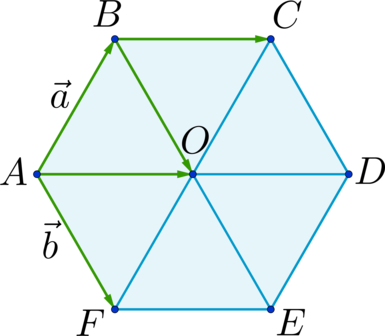
Отрезки $AD$ , $BE$ и $CF$ пересекаются в точке $O$ и делятся этой точкой пополам. $BC \parallel AD$ и $ABCO$ – параллелограмм; $AF \parallel BE$ и $ABOF$ – параллелограмм $\Rightarrow$ \[\overrightarrow = \overrightarrow = \overrightarrow + \overrightarrow = \overrightarrow + \overrightarrow = \vec + \vec\] $\Rightarrow$ $x = 1$ , $y = 1$ $\Rightarrow$ $x + y = 2$ .

Старшеклассники, которые готовятся к сдаче ЕГЭ по математике и при этом рассчитывают на получение достойных баллов, обязательно должны повторить тему «Правила сложения и вычитания нескольких векторов». Как видно из многолетней практики, подобные задания каждый год включаются в аттестационное испытание. Если у выпускника вызывают трудности задачи из раздела «Геометрия на плоскости», к примеру, в которых требуется применить правила сложения и вычитания векторов, ему обязательно стоит повторить или вновь разобраться в материале, чтобы успешно сдать ЕГЭ.

Образовательный проект «Школково» предлагает новый подход в подготовке к аттестационному испытанию. Наш ресурс выстроен таким образом, чтобы учащиеся смогли выявить наиболее сложные для себя разделы и восполнить пробелы в знаниях. Специалисты «Школково» подготовили и систематизировали весь необходимый материал для подготовки к сдаче аттестационного испытания.

Для того чтобы задачи ЕГЭ, в которых необходимо применить правила сложения и вычитания двух векторов, не вызывали затруднений, мы рекомендуем прежде всего освежить в памяти базовые понятия. Найти этот материал учащиеся смогут в разделе «Теоретическая справка».

Если вы уже вспомнили правило вычитания векторов и основные определения по данной теме, предлагаем закрепить полученные знания, выполнив соответствующие упражнения, которые подобрали специалисты образовательного портала «Школково». Для каждой задачи на сайте представлен алгоритм решения и дан правильный ответ. В теме «Правила сложения векторов» представлены различные упражнения; выполнив два-три сравнительно легких задания, учащиеся могут последовательно переходить к более сложным.

Оттачивать собственные навыки по таким, например, заданиям, как задачи на координатной плоскости, школьники имеют возможность в режиме онлайн, находясь в Москве или любом другом городе России. При необходимости задание можно сохранить в разделе «Избранное». Благодаря этому вы сможете быстро найти интересующие примеры и обсудить алгоритмы нахождения правильного ответа с преподавателем.

Источник

Вычитание векторов. Как найти разность векторов

Вы будете перенаправлены на Автор24

Откладывание вектора от данной точки

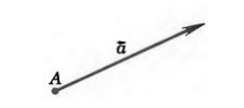
Для того, чтобы ввести разность векторов, сначала необходимо разобраться в таком понятии, как откладывание вектора от данной точки.

Читайте также: Какими способами сажают картофель

Введем следующую теорему:

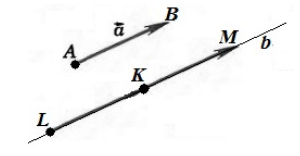
От любой точки $K$ можно отложить вектор $\overrightarrow$ и притом только один.

Доказательство.

Существование: Здесь нужно рассмотреть два случая:

В этом случае, очевидно, что искомый вектор — вектор $\overrightarrow$.

Рисунок 2. Иллюстрация теоремы 1

Единственность: единственность сразу следует из построения, проведенного в пункте «существование».

Теорема доказана.

Вычитание векторов. Правило первое

Пусть нам даны векторы $\overrightarrow$ и $\overrightarrow$.

Готовые работы на аналогичную тему

Построение разности двух векторов рассмотрим с помощью задачи.

Решение.

Рисунок 3. Разность двух векторов

По правилу треугольника для построения суммы двух векторов видим, что

Из определения 2, получаем, что

Вычитание векторов. Правило второе

Вспомним следующее необходимое нам понятие.

Вектор $\overrightarrow$ называется произвольным для вектора $\overrightarrow$, если эти векторы противоположно направлены и имеют равную длину.

Для того чтобы ввести второе правило для разности двух векторов, нам необходимо в начале ввести и доказать следующую теорему.

Доказательство.

По определению 2, имеем

Прибавим к обеим частям вектор $\left(-\overrightarrow\right)$, получим

Так как векторы $\overrightarrow$ и $\left(-\overrightarrow\right)$ противоположны, то $\overrightarrow+\left(-\overrightarrow\right)=\overrightarrow<0>$. Имеем

Теорема доказана.

Пример задачи на понятие разности векторов

Рисунок 4. Параллелограмм

Решение.

а) Произведем сложение по правилу треугольника, получим

Из первого правила разности двух векторов, получаем

б) Так как $\overrightarrow=\overrightarrow$, получим

По теореме 2, имеем

Используя правило треугольника, окончательно имеем

Источник

Сложение и вычитание векторов

Формулы сложения и вычитания векторов

Формулы сложения и вычитания векторов для плоских задач

В случае плоской задачи сумму и разность векторов a = < a_x ; a_y > и b = < b_x ; b_y > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания векторов для пространчтвенных задач

В случае пространственной задачи сумму и разность векторов a = < a_x ; a_y ; a_z > и b = < b_x ; b_y ; b_z > можно найти, воспользовавшись следующими формулами:

Формулы сложения и вычитания n -мерных векторов

В случае n -мерного пространства сумму и разность векторов a = < a ₁ ; a ₂ ; . ; a_n > и b = < b ₁ ; b ₂ ; . ; b_n > можно найти, воспользовавшись следующими формулами:

Примеры задач на сложение и вычитание векторов

Примеры плоских задач на сложение и вычитание векторов

Примеры пространственных задач на сложение и вычитание векторов

Примеры задач на сложение и вычитание векторов с размерностью большей 3

Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!

Добро пожаловать на OnlineMSchool.
Меня зовут Довжик Михаил Викторович. Я владелец и автор этого сайта, мною написан весь теоретический материал, а также разработаны онлайн упражнения и калькуляторы, которыми Вы можете воспользоваться для изучения математики.

Источник

Геометрия, 9 класс, урок: «Вычитание векторов»

ГЕОМЕТРИЯ, 9 КЛАСС, УРОК: «ВЫЧИТАНИЕ ВЕКТОРОВ»

Тема: Вычитание векторов

Знать, какой вектор является разностью двух векторов, теорему о разности векторов.

Уметь строить разность двух векторов двумя способами, применять эти знания при решении задач.

I. Организационный момент: назвать уели урока.

II. Проверка пройденного материала:

1. Как называются векторы, имеющие равные модули и противоположно направленные?

Читайте также: Плед крючком легкий способ
Б) противоположно направленные

2. Тело переместили из точки А в точку В, а потом из точки В в точку С. Какой вектор представляет суммарное перемещение тела?

А)

Б)

В)

3. Закончите предложение:

Суммой двух векторов называется вектор, построенный по правилу. (треугольника)

4. Вставьте пропущенное слово:

Чтобы сложить два неколлинеарных вектора и, нужно отложить от произвольной точки О векторы = и = и построить. ОАСВ, тогда =+

5. Изображенный на рисунке способ построения суммы нескольких векторов называется правилом.

III. Объяснение нового материала:

Вычитание векторов, как и вычитание чисел, — это действие, обратное сложению. Разность двух векторов и называется такой вектор , который в сумме с вектором дает вектор . Разность векторов и обозначается так: — . Построить разность векторов и можно следующим образом. Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда вектор и будет разностью — , поскольку

=+. Итак, == — = — .

Вычитание векторов можно свести к сложению точно так же, как и в случае чисел а и b:

а — b = а + (- b), где числа b и + (- b) — противоположные.

Итак, нам надо доказать, что результат вычитания вектора из вектора тот же, что и результат сложения векторов а + (- b).

2. Теорема о разности двух векторов.

Теорема (о разности векторов)

Для любых векторов и справедливо равенство — = + (- ).

Отложим от произвольной точки О векторы и . Получим векторы = и =. Тогда, согласно определению, разность векторов и есть вектор , т. е. = — = — . По правилу треугольника = + . Кроме того, = — = —. Поэтому — = = + = (-) + =+(-)=+(-). Теорема доказана.

3. Построение разности векторов.

Доказанная теорема подсказывает еще один способ построения разности векторов и .

Отложим от произвольной точки О отложим вектор = , затем от точки А отложим вектор = —. Тогда по теореме о разности двух векторов — = + (-), поэтому — = + = . Итак, мы построили разность векторов и .

Выводы по уроку:

1. Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор .

2. Теорема ( о разности двух векторов): Для любых векторов и справедливо равенство:

— = + (-).

IV. Закрепление полученных знаний.

А) Разностью двух векторов и называется такой вектор , построенный по правилу треугольника.

Б) Разностью двух векторов и называется такой вектор , который получается после ряда последовательных сложений

В) Разностью двух векторов и называется такой вектор , который в сумме с вектором дает вектор

2. Какой вектор, изображенный на рисунке, является разностью векторов и ?

А)

Б)

В)

3. № 000. Дан треугольник АВС. Выразите векторы = и = вектор .

а) —

б) —

в) +

4. № 000. Сторона равностороннего треугольника АВС равна а. Модуль ½ — ½ = а

V. Подведение итогов.

VI. Задание на дом: п.82, №№ 000, 756, 767

Источник