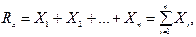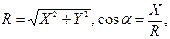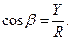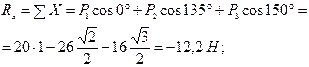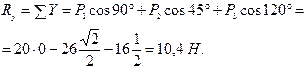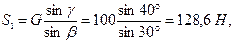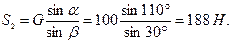- Техническая механика
- Пространственная система сил
- Пространственная система сходящихся сил
- Разложение силы по трем осям координат
- Аналитический способ определения равнодействующей пространственной системы сходящихся сил
- Аналитические условия равновесия пространственной системы сходящихся сил
- Момент силы относительно оси
- Аналитические условия равновесия пространственной системы произвольно расположенных сил
- Теорема о моменте равнодействующей относительно оси (теорема Вариньона)
- Аналитическое определение равнодействующей
Техническая механика
Пространственная система сил
Пространственная система сходящихся сил
Система сил, линии действия которых расположены в различных плоскостях, называется пространственной системой сил .
Пространственная система сил называется сходящейся , если линии действия всех сил системы пересекаются в одной точке.
Теорема: пространственная система сходящихся сил эквивалентна равнодействующей, которая равна векторной сумме этих сил; линия действия равнодействующей проходит через точку пересечения линий действия составляющих сил.
Пусть дана пространственная система n сходящихся сил (F1, F2, F3. Fn) . На основании следствия из аксиом III и IV перенесем все силы системы вдоль линий действия в точку их пересечения. Затем на основании аксиомы параллелограмма последовательно сложим все силы и получим их равнодействующую:
Силовой многоугольник пространственной системы сил не лежит в одной плоскости, поэтому геометрический и графический способы нахождения равнодействующей пространственной системы сходящихся сил неприемлемы, а применяется только аналитический способ (метод проекций) .
Проекция силы на ось в пространстве находится по проецирующим перпендикулярам, и может быть определена при помощи тригонометрических функций. При определении проекций сил пространственной системы потребуется система координат с осями X , Y , Z , поскольку силы системы не располагаются в одной плоскости.
Правило знаков для проекций будет таким же, как и для плоской системы сил – совпадающие по направлению с координатной осью силы считаются положительными, в противном случае – отрицательными. Если вектор силы параллелен какой-либо оси координат, то он проецируется на эту ось в натуральную величину, если же вектор перпендикулярен оси, его проекция на эту ось будет равна нулю.
Разложение силы по трем осям координат
Пусть дана сила F (см. рисунок 1) .

Достроим полученное изображение до параллелепипеда, у которого составляющие Fx , Fy и Fz являются ребрами, а сила F – диагональю.
Из изложенного можно сделать вывод: равнодействующая трех взаимно-перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах .
Из рисунка видно, что в случаях разложения силы F по трем взаимно-перпендикулярным направлениям x , y , z составляющие Fx , Fy и Fz равны по модулю проекциям силы F на эти оси.
Зная проекции силы на три взаимно-перпендикулярные оси координат, можно определить модуль и направление вектора силы по формулам:
модуль силы: F = √(Fx 2 + Fy 2 + Fz 2 ) (здесь и далее √ — знак корня) ;
направляющие косинусы: cos(F,x) = Fx/F; cos(F,y) = Fy/F; cos(F,z) = Fz/F .
Аналитический способ определения равнодействующей пространственной системы сходящихся сил
Рассмотренный выше способ разложения силы F на три составляющие по направлению координатных осей x , y , z можно применить для каждой из сходящихся сил пространственной системы. Тогда вместо данной системы n сходящихся сил мы получим эквивалентную ей систему 3n сил, из которых n сил действуют по оси x , n сил – по оси y , и n сил – по оси z .
Равнодействующая проекций сил системы на ось x равна их геометрической сумме, то же самое можно сказать и о равнодействующих проекций сил на оси y и z .
Таким образом, систему 3n сил можно заменить эквивалентной ей системой трех сил, каждая из которых представляет собой равнодействующую проекций сил данной системы на ту или иную ось координат.
Проекции силы на три взаимно-перпендикулярные оси и составляющие силы, направленные по этим осям, равны по модулю, следовательно, проекции равнодействующей равны:
Очевидно, что равнодействующая трех взаимно перпендикулярных сил выражается по модулю и направлению диагональю параллелепипеда, построенного на этих силах, и по известным проекциям равнодействующей можно определить модуль и направление самой равнодействующей.
Аналитические условия равновесия пространственной системы сходящихся сил
Известно, что пространственная система сходящихся сил эквивалентна равнодействующей. Если такая система сил находится в равновесии, т. е. эквивалентна нулю, то можно сделать вывод, что равнодействующая этой системы равна нулю, а следовательно, и проекции равнодействующей тоже равны нулю, причем эти проекции равны сумме проекций составляющих.
Отсюда вытекают условия равновесия пространственной системы сходящихся сил:
ΣX = 0; ΣY = 0; ΣZ = 0 .
Эти условия формируются следующим образом: для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую их трех координатных осей равнялась нулю.
Момент силы относительно оси
Рассмотрим колесо червячной передачи, укрепленное на валу, вращающемся в подшипниках (см. рисунок 2) . Червяк передает червячному колесу силу F , не лежащую в плоскости, перпендикулярной оси.
Разложим силу F на три взаимно-перпендикулярные составляющие F1 , F2 и F3 .
Составляющую F1 назовем окружной силой , составляющую F2 – осевой силой , а составляющую F3 – радиальной силой .
Из рисунка видно, что составляющая F1 вызывает вращательное действие, которое измеряется произведением силы F1 на радиус колеса r ; составляющая F2 стремится сдвинуть червячное колесо вдоль оси, а составляющая F3 стремится изогнуть ось колеса.
Очевидно, что вращающее действие сил F2 и F3 относительно оси колеса равно нулю.
Таким образом, если нужно найти момент силы относительно оси, то следует принимать в расчет только составляющую F1 , лежащую в плоскости, перпендикулярной оси, и не пересекающую ось (иначе ее момент будет равен нулю).
Ранее было отмечено, что проекция вектора силы на ось есть скалярная алгебраическая величина. В отличие от проекции на ось проекция силы на плоскость есть величина векторная, так как эта проекция характеризуется не только числовым значением, но и положением на плоскости, т. е. направлением.
Поэтому моменту силы относительно оси можно дать такое определение: моментом силы относительно оси называется величина, равная моменту проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с плоскостью.
Это определение поясняет рисунок 3 .
Момент силы относительно оси условимся записывать следующим образом:
Условимся считать момент силы положительным, если смотреть с положительного конца оси и сила стремится вызвать вращение против часовой стрелки, если же сила стремится вызвать вращение по часовой стрелке, ее момент считаем отрицательным.
Момент силы относительно оси не меняется при перемещении силы вдоль оси ее действия.
Момент силы будет равен нулю в двух случаях (не считая случаев, когда сила равна нулю или направлена вдоль оси):
- если вектор силы параллелен оси, так как при этом проекция силы на плоскость, перпендикулярную оси, равна нулю (см. рисунок 3, сила FZ) ;
- если линия действия силы пересекает ось, так как при этом плечо равно нулю (сила F3 на рисунке 2) .
Аналитические условия равновесия пространственной системы произвольно расположенных сил
Пространственная система сил, в которой линии действия составляющих сил расположены произвольно, т. е. линии их действия могут не пересекаться и находиться в разных плоскостях, называется произвольно расположенной системой сил.
Для равновесия пространственной системы произвольно расположенных сил необходимо и достаточно, чтобы алгебраическая сумма проекций всех сил на каждую из трех осей координат была равна нулю и чтобы алгебраическая сумма моментов всех сил относительно каждой из этих осей была равна нулю.
Строгое обоснование приведенного выше условия равновесия пространственной системы произвольно расположенных сил требует знания некоторых вопросов, не предусмотренных программами учреждений среднего профессионального образования, поэтому условие равновесия такой системы здесь приводится без доказательства.
Математически условие равновесия пространственной системы произвольно расположенных сил можно записать в виде уравнений:
- ΣX = 0; ΣMx(Fi) = 0;
- ΣY = 0; ΣMy(Fi) = 0;
- ΣZ = 0; ΣMz(Fi) = 0.
Свободное тело в пространстве имеет шесть степеней свободы, а именно: возможность перемещаться в направлениях трех взаимно-перпендикулярных осей координат и возможность вращаться вокруг этих осей. Таким образом, шести степеням свободы тела в пространстве соответствуют шесть условий равновесия.
Если система сил, приложенных к свободному телу, удовлетворяет всем шести условиям равновесия, то возможность трех перемещений и трех вращений тела под действием сил системы исключена, поэтому тело будет находится в равновесии.
Очевидно, что все выведенные ранее условия равновесия для различных систем сил являются частными случаями условия равновесия пространственной системы произвольно расположенных сил.
Так как условия равновесия пространственной системы сил справедливы для любых прямоугольных осей координат, то при решении данной задачи систему координат можно изменять, т. е. часть уравнений равновесия составить для одних осей координат, а часть – для измененных. В некоторых случаях этот прием упрощает решение задач.
Теорема о моменте равнодействующей относительно оси
(теорема Вариньона)
Теорема: момент равнодействующей относительно оси равен алгебраической сумме моментов, составляющих сил относительно этой же оси .
Пусть даны пространственная система n произвольно расположенных сил, приложенных к телу, и равнодействующая этой системы сил FΣ (см. рисунок 4) :
Приложим к телу другую систему сил, равнодействующая которой F’Σ по модулю равна FΣ и направлена по той же линии действия, но в противоположную сторону, т. е. является уравновешивающей данной системы сил.
Тогда можно записать:
Так как обе записанные выше системы сил эквивалентны нулю, т. е. уравновешены, то к ним можно применить любое условие равновесия, например
Запишем это условие для обеих систем:
Так как правые части этих равенств равны, то будут равны и левые :
Сократив общее слагаемое Mx(F’Σ) , получим:
Источник
Аналитическое определение равнодействующей
Равнодействующую системы сходящихся сил можно определить и аналитически (способом проекций). Для этого необходимо воспользоваться теоремой: проекция равнодействующей на данную ось равна алгебраической сумме проекций слагаемых сил на ту же ось.
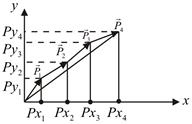
Проекции равнодействующей на координатные оси х и у определяются как суммы проекций составляющих.

Для удобства и простоты индекс и пределы суммирования ставить не будем:
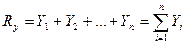
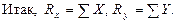
Зная проекции, определяют модуль и направление равнодействующей по формулам:
При решении задач на сложение плоской системы сходящихся сил аналитическим способом необходимо: выбрать систему координатных осей х и у;найти углы каждой силы с координатными осями, а затем, определив проекции равнодействующей, найти ее модуль и направление.
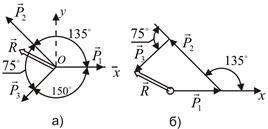
Пример 4.Даны силы P1 = 20 Н, P2 = 26 Н, P3 = 16 Н, приложенные к точке О. Силы составляют между собой следующие углы: 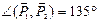
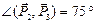
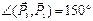
Определить равнодействующую 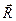




|
|
|
|
|
|
|
Решение. Примем точку О за начало координат, линию действия силы 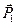
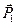
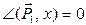
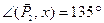
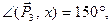
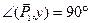
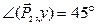
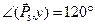
Определим проекции равнодействующей:
Тогда модуль и направление равнодействующей равны:
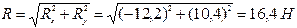
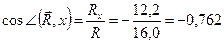
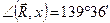
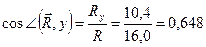
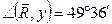
Этот же результат можно получить и геометрически, построив в определенном масштабе силовой многоугольник (рис. 4.12, б).
Метод проекции при решении задач на равновесие системы особенно удобен в том случае, если в систему входит более трёх сил.
4.6. Геометрическое и аналитическое условия
равновесия системы сходящихся сил
Необходимым и достаточным условием равновесия плоской системы сходящихся сил является равенство нулю равнодействующей этой системы сил. Это условие можно выразить одним векторным равенством:
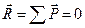
или двумя алгебраическими (скалярными) равенствами:
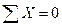
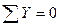
Векторное равенство выражает условие замкнутости многоугольника данных сил, т.е. условие равновесия плоской системы сходящихся сил в геометрической форме (4.10).
Равенства выражают условие равновесия плоской системы сходящихся сил в аналитической форме (4.11), и их называют условиями равновесия плоской системы сходящихся сил: для равновесия плоской системы сходящихся сил необходимо и достаточно, чтобы алгебраические суммы проекций всех сил на координатные оси были равны нулю.
Методические указания к решению задач
геометрическим способом
При решении задач геометрическим (графическим) способом необходимо придерживаться следующего порядка.
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить все активные (заданные) силы, действующие на выделенное тело.
3. Освободить это тело от наложенных на него связей, заменив их действие реакциями связей.
4. Построить замкнутый силовой многоугольник (или треугольник, если действуют три силы). При этом следует сначала сложить все заданные, а затем достроить неизвестные силы.
5. Решить силовой многоугольник (по известным элементам определить неизвестные) или, если силовой многоугольник построен в масштабе, определить искомые силы по масштабу.
Методические указания к решению задач
аналитическим способом
При решении задач аналитическим способом рекомендуется придерживаться следующего порядка.
1. Выделить тело (или точку), равновесие которого следует рассмотреть.
2. Изобразить активные (заданные) силы, действующие на выделенное тело.
3. Освободить тело от наложенных на него связей, заменив их действие реакциями связей.
4. Выбрать систему координат. Координатные оси следует по возможности направлять по неизвестным силам, тогда проекция неизвестной силы на перпендикулярную ей ось окажется равной нулю. Благодаря этому в уравнение равновесия войдет только одно неизвестное.
5. Составить уравнения равновесия плоской системы сил: 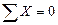
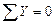
6. Решить уравнения равновесия относительно искомых величин.
Преимущества аналитического способа проекций перед геометрическим способом силового многоугольника особенно заметны в задачах на равновесие системы более трёх сил. Действительно, решение силового четырёх-, пяти- и n-угольника представляет известные трудности, в то время как решение методом проекций не усложняется при увеличении числа проектируемых сил.
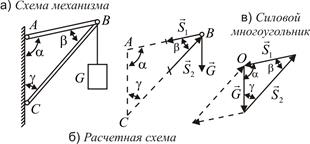
Пример 5. В шарнире В кронштейна ABC подвешен груз весом G = 100 Н. Определить усилия в стержнях кронштейна, если a = 110°, b = 30°, g = 40°. Стержни прикреплены к стене шарнирно (рис. 4.13, а).
|
|
|
Решение. Рассмотрим равновесие шарнира В (рис. 4.13, б). К нему приложена активная сила 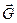
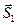
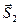
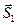
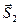
Для решения применим геометрический способ. Поскольку шарнир находится в равновесии, то силовой треугольник, составленный из этих сил, должен быть замкнут. Из некоторой точки О (рис. 4.13, в) в выбранном масштабе строим вектор 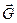
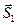
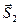
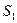
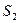
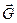
Модули 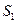
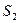
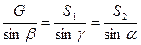
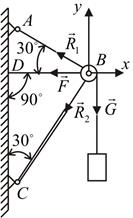
Пример 6. На оси шарнира В свободно вращается блок (рис. 4.14). Через блок перекинута нить, с помощью которой удерживается груз весом G = 50 Н. Определить усилия в стержнях АВ и ВС. При этом диаметром блока, трением нити можно пренебречь.
Решение. Для решения применим аналитический метод.
1. Выделим точку, равновесие которой следует рассмотреть: в данной задаче это будет точка В неподвижного блока.
2. Изобразим векторы всех активных сил, действующих на нее: в нашем примере это натяжение вертикальной ветви нити и натяжение горизонтальной ветви нити, равные весу груза.
3. Мысленно отбросим связи и заменим их реакциями 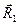
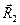
4. Все силы изобразим в виде векторов, предположив, что стержни АВ и ВС растянуты, направив соответственно 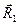
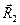
Выбрав направление координатных осей х и у,составим два уравнения равновесия:
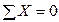
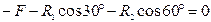
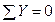
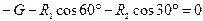
Рис. 4.14. Шарнирно-стержневая система
Учитывая, что F = G = 50 Н, решив совместно оба уравнения, получим R1= – 18,6 Н; R2= – 68,5 Н. Здесь знак «–» указывает на то, что стержни АВ и ВС сжаты, а не растянуты, как мы предполагали ранее.
Контрольные вопросы
1. Как влияет угол между двумя сходящимися силами на модуль их равнодействующей?
2. Какие условия необходимы для того, чтобы задача разложения силы на две составляющие была определённой?
3. Для чего и как строится силовой многоугольник?
4. В чем заключается геометрическое условие равновесия плоской системы сходящихся сил?
5. Чему равна проекция силы на ось?
6. В каких случаях проекция силы на ось равна нулю, и в каких случаях она равна модулю силы?
7. Как определяется знак проекции силы на ось?
8. Как найти модуль и направление силы, если известны ее проекции на две взаимно перпендикулярные оси координат?
9. В чем заключаются аналитические условия равновесия плоской системы сходящихся сил?
Дата добавления: 2015-12-26 ; просмотров: 14375 ; ЗАКАЗАТЬ НАПИСАНИЕ РАБОТЫ
Источник