Виды умножения
проблема : разобраться видах умножения
Цель:ознакомление с различными способами умножения натуральных чисел, не используемых на уроках, и их применение при вычислениях числовых выражений.
Задачи:
1. Найти и разобрать различные способы умножения.
2. Научиться демонстрировать некоторые способы умножения.
3. Рассказать о новых способах умножения и научить ими пользоваться учащихся.
4. Развить навыки самостоятельной работы: поиск информации, отбор и оформление найденного материала.
5. Эксперимент «какой способ быстрей»
Гипотеза:Надо ли знать таблицу умножения?
Актуальность:В последнее время ученики доверяют гаджетам больше чем себе. И по этому считают только на калькуляторах. Мы хотели показать что есть разные способы умножение, что бы ученикам было легче считать,и интересно учить.
ВВЕДЕНИЕ
Вы не сможете выполнить умножения многозначных чисел — хотя бы даже двузначных — если не помните наизусть всех результатов умножения однозначных чисел, т. е. того, что называется таблицей умножения.
В разное время разные народы владели разными способами умножения натуральных чисел.
Почему же сейчас все народы применяют один способ умножения «столбиком»?
Почему люди отказались от старых способов умножения в пользу современного?
Имеют ли забытые способы умножения право на существование в наше время?
Что бы ответить на эти вопросы я проделал следующую работу:
1. С помощью сети Интернета нашел информацию о некоторых способах умножения, которые использовались раньше.;
2. Изучил литературу, предложенную учителем;
3. Решил пару примеров всеми изученными способами, что бы узнать их недостатки;
4) Выявил среди них наиболее эффективные;
5. Провел эксперимент;
6. Сделал выводы.
1. Найти и разобрать различные способы умножения.
Умножение на пальцах.
Древнерусский способ умножения на пальцах является одним из наиболее употребительных методов, которым успешно пользовались на протяжении многих столетий российские купцы. Они научились умножать на пальцах однозначные числа от 6 до 9. При этом достаточно было владеть начальными навыками пальцевого счета “единицами”, “парами”, “тройками”, “четверками”, “пятерками” и “десятками”. Пальцы рук здесь служили вспомогательным вычислительным устройством.
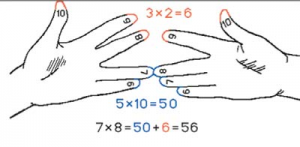
Для этого на одной руке вытягивали столько пальцев, на сколько первый множитель превосходит число 5, а на второй делали то же самое для второго множителя. Остальные пальцы загибали. Потом бралось число (суммарное) вытянутых пальцев и умножалось на 10, далее перемножались числа, показывавшие, сколько загнуто пальцев на руках, а результаты складывались.
Например, умножим 7 на 8. В рассмотренном примере будет загнуто 2 и 3 пальца. Если сложить количества загнутых пальцев (2+3=5) и перемножить количества не загнутых (2•3=6), то получатся соответственно числа десятков и единиц искомого произведения 56 . Так можно вычислять произведение любых однозначных чисел, больше 5.
Способы умножения чисел в разных странах
Умножение на 9.
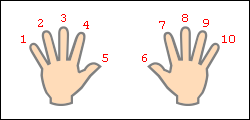
Умножение для числа 9 — 9·1, 9·2 … 9·10 — легче выветривается из памяти и труднее пересчитывается вручную методом сложения, однако именно для числа 9 умножение легко воспроизводится «на пальцах». Растопырьте пальцы на обеих руках и поверните руки ладонями от себя. Мысленно присвойте пальцам последовательно числа от 1 до 10, начиная с мизинца левой руки и заканчивая мизинцем правой руки (это изображено на рисунке).
Кто придумал умножение на пальцах
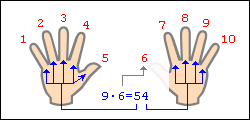
Допустим, хотим умножить 9 на 6. Загибаем палец с номером, равным числу, на которое мы будем умножать девятку. В нашем примере нужно загнуть палец с номером 6. Количество пальцев слева от загнутого пальца показывает нам количество десятков в ответе, количество пальцев справа — количество единиц. Слева у нас 5 пальцев не загнуто, справа — 4 пальца. Таким образом, 9·6=54. Ниже на рисунке детально показан весь принцип «вычисления».
Умножение необычным способом
Еще пример: нужно вычислить 9·8=?. По ходу дела скажем, что в качестве «счетной машинки» не обязательно могут выступать пальцы рук. Возьмите, к примеру, 10 клеточек в тетради. Зачеркиваем 8-ю клеточку. Слева осталось 7 клеточек, справа — 2 клеточки. Значит 9·8=72. Все очень просто.
7 клеток 2 клетки.
Индийский способ умножения.
Самый ценный вклад в сокровищницу математических знаний был совершен в Индии. Индусы предложили употребляемый нами способ записи чисел при помощи десяти знаков: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0.
Основа этого способа заключается в идее, что одна и та же цифра обозначает единицы, десятки, сотни или тысячи, в зависимости от того, какое место эта цифра занимает. Занимаемое место, в случае отсутствия каких – нибудь разрядов, определяется нулями, приписываемыми к цифрам.
Индусы отлично считали. Они придумали очень простой способ умножения. Они умножение выполняли, начиная со старшего разряда, и записывали неполные произведения как раз над множимым, поразрядно. При этом сразу был виден старший разряд полного произведения и, кроме того, исключался пропуск какой-либо цифры. Знак умножения еще не был известен, поэтому между множителями они оставляли небольшое расстояние. Например, умножим их способом 537 на 6:
(300 + 3 ∙ 6 = 318) 318
(3180 +7 ∙ 6 = 3222) 3222
6
Умножение способом «МАЛЕНЬКИЙ ЗАМОК».
Умножение чисел сейчас изучают в первом классе школы. А вот в Средние века совсем немногие владели искусством умножения. Редкий аристократ мог похвастаться знанием таблицы умножения, даже если он окончил европейский университет.
За тысячелетия развития математики было придумано множество способов умножения чисел. Итальянский математик Лука Пачоли в своём трактате «Сумма знаний по арифметике, отношениям и пропорциональности»(1494 г.) приводит восемь различных методов умножения. Первый из них носит название «Маленький замок», а второй не менее романтичное название «Ревность или решетчатое умножение».
Преимущество способа умножения «Маленький замок» в том, что уже с самого начала определяются цифры старших разрядов, а это бывает важно, если требуется быстро оценить величину.
Цифры верхнего числа, начиная со старшего разряда, поочередно умножаются на нижнее число и записываются в столбик с добавлением нужного числа нулей. Затем результаты складываются.
Способы умножения чисел в разных странах
Умножение чисел методом «ревность».
«Методы умножения Второй способ носит романтическое название ревность», или «решётчатое умножение».
Сначала рисуется прямоугольник, разделённый на квадраты, причём размеры сторон прямоугольника соответствуют числу десятичных знаков у множимого и множителя. Затем квадратные клетки, делятся по диагонали, и «…получается картинка, похожая на решётчатые ставни-жалюзи, — пишет Пачоли. – Такие ставни вешались на окна венецианских домов, мешая уличным прохожим видеть, сидящих у окон дам и монахинь».
Умножим этим способом 347 на 29. Начертим таблицу, запишем над ней число 347, а справа число 29.
В каждую строчку запишем произведение цифр, стоящих над этой клеткой и справа от нее, при этом цифру десятков произведения напишем над косой чертой, а цифру единиц – под ней. Теперь складываем числа в каждой косой полосе, выполняя эту операцию, справа налево. Если сумма окажется меньше 10, то ее пишем под нижней цифрой полосы. Если же она окажется больше, чем 10, то пишем только цифру единиц суммы, а цифру десятков прибавляем к следующей сумме. В результате получаем искомое произведение 10063.
Крестьянский способ умножения.
Самым, на мой взгляд, «родным» и легким способом умножения является способ, который употребляли русские крестьяне. Этот прием вообще не требует знания таблицы умножения дальше числа 2. Сущность его в том, что умножение любых двух чисел сводится к ряду последовательных делений одного числа пополам при одновременном удвоении другого числа. Деление пополам продолжают до тех пор, пока в частном не получится 1, параллельно удваивая другое число. Последнее удвоенное число и дает искомый результат.
В случае нечетного числа надо откинуть единицу и делить остаток пополам; но зато к последнему числу правого столбца нужно будет прибавить все те числа этого столбца, которые стоят против нечетных чисел левого столбца: сумма и будет искомым произведением
Произведение всех пар соответственных чисел одинаковое, поэтому
37 ∙ 32 = 1184 ∙ 1 = 1184
В случае, когда одно из чисел нечетное или оба числа нечетные, поступаем следующим образом:
24 ∙ 17 = 24∙(16+1)=24 ∙ 16 + 24 = 384 + 24 = 408
Новый способ умножения.
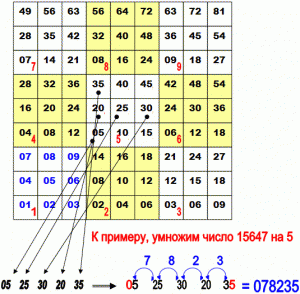
Интересен новый способ умножения, о котором недавно появились сообщения. Изобретатель новой системы устного счёта кандидат философских наук Василий Оконешников утверждает, что человек способен запоминать огромный запас информации, главное – как эту информацию расположить. По мнению самого учёного, наиболее выигрышной в этом отношении является девятеричная система – все данные просто располагают в девяти ячейках, расположенных, как кнопочки на калькуляторе.
Считать по такой таблице очень просто. К примеру, умножим число 15647 на 5. В части таблицы, соответствующей пятёрке, выбираем числа, соответствующие цифрам числа по порядку: единице, пятёрке, шестёрке, четвёрке и семёрке. Получаем: 05 25 30 20 35
Левую цифру (в нашем примере — ноль) оставляем без изменений, а следующие цифры складываем попарно: пятёрку с двойкой, пятёрку с тройкой, ноль с двойкой, ноль с тройкой. Последняя цифра также без изменений.
В итоге получаем: 078235. Число 78235 и есть результат умножения.
Если же при сложении двух цифр получается число, превосходящее девять, то его первая цифра прибавляется к предыдущей цифре результата, а вторая пишется на «своё» место.
Умножение графическим методом (линейным, китайским)
Перемножим два двузначных числа: 15*23
Шаг 1. первое число 15:
Рисуем первую цифру – одной линией.
Рисуем вторую цифру – пятью линиями.
Шаг 2. второе число 23:
Рисуем первую цифру – двумя линиями.
Рисуем вторую цифру – тремя линиями.
Шаг 3.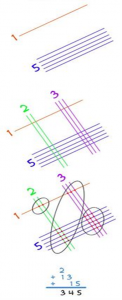
Шаг 4. Результат – 345

Проведем эксперимент
С помощью секундомера установим сколько времени затрачивается на решение примера, каждым рассмотренным способом.
Заключение.
Работая над этой темой, я узнал, что существует порядка 30 различных, забавных и интересных способов умножения. Некоторыми в различных странах пользуются до сих пор. Я выбрал для себя некоторые интересные способы. Но не все способы удобны в использовании, особенно при умножении многозначных чисел.
Источник
Способы умножения многозначных чисел
Рецензия на научно-исследовательскую работу учащегося.
- Исследовательская работа выполнена учеником 7 «А» класса МБОУ «СОШ № 2» Агафуровым Максимом.
- Руководитель исследования: учитель математики – Лукьянова О.А.
- Тема работы: «Необычные способы умножения». Вид работы: реферативная. Данная работа является актуальной на сегодняшний день, т.к. знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результатах вычислений, выполненных с помощью калькулятора. Кроме того, освоение вычислительных навыков развивает память и помогает школьникам полноценно усваивать предметы физико-математического цикла.
- Выполнена исследовательская часть работы. Изложены объяснения данных примеров и сделаны соответствующие выводы.
- Цели и задачи научно-исследовательской работы сформулированы грамотно, соответствуют заявленной теме.
- Специальная литература изучена качественно с достаточной глубиной.
- Выводы научно-исследовательской работы логичны, теоретически обоснованы.
- В работе представлена исследовательская часть на достаточном уровне. Ее описание соответствует выводам. Большая часть работы выполнялась в основном самостоятельно, с небольшими направляющими советами и действиями руководителя.
Скачать:
| Вложение | Размер |
|---|---|
| Научно-исследовательская работа «Необычные способы умножения» | 36.81 КБ |
| Презентация | 1.48 МБ |
Предварительный просмотр:
Способы умножения многозначных чисел
1.1.«Ревность, или решётчатое умножение»……………………………..4
1.2.«Русский крестьянский способ»………………………………………5
1.3. «Китайский способ умножения»……………………………………. 6
2.1. Возведение в квадрат любого двузначного числа…………………. 6
2.2. Квадрат числа, близкого к «круглому»………………………………7
2.4. Новый способ возведения в квадрат чисел от 40 до 60………………7
2.5. Возведение в квадрат числа, оканчивающегося на 5…………………8
2.6 Возведение в квадрат числа, оканчивающегося на 1…………………8
2.7. Возведение в квадрат числа, оканчивающегося на 6…………………8
2.8. Возведение в квадрат числа, оканчивающегося на 9…………………8
2.9. Возведение в квадрат числа, оканчивающегося на 4…………………8
Введение « Счет и вычисления –
основы порядка в голове».
Иоганн Генрих Песталоцци (1746 — 1827)
Кто с детских лет занимается математикой, тот развивает внимание, тренирует свой мозг, свою волю, воспитывает настойчивость и упорство в достижении цели.
Актуальность: Математика является одной из важнейших наук на земле и именно с ней человек встречается каждый день в своей жизни. Счет в уме является самым древним и простым способом вычисления. Знание упрощенных приемов устных вычислений остается необходимым даже при полной механизации всех наиболее трудоемких вычислительных процессов. Устные вычисления дают возможность не только быстро производить расчеты в уме, но и контролировать, оценивать, находить и исправлять ошибки в результатах вычислений, выполненных с помощью калькулятора. Кроме того, освоение вычислительных навыков развивает память и помогает школьникам полноценно усваивать предметы физико-математического цикла.
Человеку в повседневной жизни невозможно обойтись без вычислений. Поэтому на уроках математики, нас в первую очередь учат выполнять действия над числами, то есть считать. Умножаем, делим, складываем и вычитаем мы привычными для всех способами, которые изучаются в школе.
Мне стало интересно, а есть ли еще какие-нибудь способы вычислений? Оказалось, что можно умножать не только так, как предлагают нам в учебниках математики, но и по-другому. Используя интернет-ресурсы, я узнал много необычных способов умножений. Ведь способность быстро производить вычисления вызывает откровенное удивление.
- Найти как можно больше необычных способов вычислений.
- Научиться их применять.
- Выбрать для себя самые интересные, чем те, которые предлагаются в школе, и использовать их при счете.
1. Познакомиться со старинными способами умножения, такими как: «Ревность, или решётчатое умножение», «Маленький замок», «Русский крестьянский способ», «Линейный способ».
2. Исследовать приемы устного возведения чисел в квадрат и применять их на практике.
Те способы вычислений, которыми мы пользуемся сейчас, не всегда были так просты и удобны. В старину пользовались более громоздкими и медленными приемами. И если бы школьник 21 века мог перенестись на пять веков назад, он поразил бы наших предков быстротой и безошибочностью своих вычислений. Молва о нем облетела бы окрестные школы и монастыри, затмив славу искуснейших счетчиков той эпохи, и со всех сторон приезжали бы учиться у нового великого мастера.
Особенно трудны в старину были действия умножения и деления. Тогда не существовало одного выработанного практикой приема для каждого действия. Напротив, в ходу была одновременно чуть не дюжина различных способов умножения и деления — приемы один другого запутаннее, запомнить которые не в силах был человек средних способностей. Каждый учитель счетного дела держался своего излюбленного приема, каждый «магистр деления» (были такие специалисты) восхвалял собственный способ выполнения этого действия. За тысячелетия развития математики было придумано много способов умножения. Кроме таблицы умножения, все они громоздкие, сложные и трудно запоминаются. Считалось, что для овладения искусством быстрого умножения нужно особое природное дарование. Простым людям, не обладающим особым математическим даром, это искусство было недоступно.
И все эти приемы умножения — «шахматный или органчиком», «загибанием», «крестиком», «решеткой», «задом наперед», «алмазом» и прочие соперничали друг с другом и усваивались с большим трудом.
Давайте рассмотрим наиболее интересные и простые способы умножения.
1.1. «Ревность, или решётчатое умножение»
Итальянский математик 15 века Лука Пачоли приводит 8 способов умножения. На мой взгляд, самые интересные из них – «ревность или решетчатое умножение» и «маленький замок».
Умножим 347 на 29.
Рисуем прямоугольник, делим его на квадраты, квадраты делим по диагонали. Получается картинка, похожая на решетчатые ставни венецианских домов. От этого и произошло название метода.
Вверху таблицы запишем число 347, а справа сверху вниз – 29
В каждый квадрат впишем произведение цифр, расположенных в одной строке и одном столбце с этим квадратом. Десятки располагаются в верхнем треугольнике, а единицы – в нижнем. Цифры складываются вдоль каждой диагонали. Результаты записываются слева и справа от таблицы.
Неудобства этого способа заключаются в трудоёмкости построения прямоугольной таблицы, а сам процесс умножения интересен и заполнение таблицы напоминает игру.
1.2. «Русский крестьянский способ»
В России среди крестьян был распространен способ, который не требовал знания всей таблицы умножения. Здесь необходимо лишь умение умножать и делить числа на 2.
Напишем одно число слева, а другое справа на одной строке Левое число будем делить на 2, а правое – умножать на 2 и результаты записывать в столбик. Если при делении возник остаток, то его отбрасывают. Умножение и деление на 2 продолжают до тех пор, пока слева не останется 1.
Затем вычеркиваем те строчки из столбика, в которых слева стоят четные числа. Теперь сложим оставшиеся числа в правом столбце.
1.3.Китайский способ умножения.
А теперь представим метод умножения, бурно обсуждаемый в Интернете, который называют китайским. При умножении чисел считаются точки пересечения прямых, которые соответствуют количеству цифр каждого разряда обоих множителей.
На листе бумаги поочередно рисуем линии, количество которых определяется из данного примера.
Сначала 32: 3 красные линии и чуть ниже — 2 синие. Затем 21: перпендикулярно уже нарисованным, рисуем сначала 2 зеленые, затем — 1 малиновую . ВАЖНО: линии первого числа рисуются в направлении из верхнего левого угла в нижний правый, второго числа — из нижнего левого, в верхний правый . Затем считаем количество точек пересечения в каждой из трех областей (на рисунке области обозначены в виде окружностей). Итак, в первой области ( область сотен) — 6 точек, во второй (область десятков) — 7 точек, в третьей (область единиц) — 2 точки. Следовательно, ответ: 672.
2. Исследовательская часть
Приёмы быстрого счета развивают память. Это касается не только математики, но и других предметов, которые изучаются в школе.
Также хочется добавить в работу способы устного возведения чисел в квадрат без использования калькулятора и, что является необходимым при решении задач ГИА и ЕГЭ, а так же является хорошей тренировкой ума.
А теперь перейдем к некоторым интересным и мне понравившимся способам устного возведения чисел в квадрат, применяемых на уроках алгебры и геометрии.
2.1. Возведение в квадрат любого двузначного числа.
Если запомнить квадраты всех чисел от 1 до 25, то легко найти и квадрат любого двузначного числа, превышающего 25.
Для того чтобы найти квадрат любого двузначного числа, надо разность между этим числом и 25 умножить на 100 и к получившемуся произведению прибавить квадрат дополнения данного числа до 50 или квадрат избытка его над 50-ю.
37 2 =12*100+13 2 =1200+169=1369
(М–25)*100+ (50-M) 2 =100M-2500+2500–100M+M 2 =M 2 .
2.2.Квадрат числа, близкого к «круглому».
Вычисление квадратов в разобранных примерах основано на формуле
а ² = ( а + в ) ( а – в ) + в ²,
в которой удачный подбор числа в сильно облегчает выкладки: во-первых, один из сомножителей должен оказаться «круглым» числом (желательно, чтобы ненулевой его цифрой была только первая), во-вторых, само число в должно легко возводиться в квадрат, т. е. должно быть небольшим. Эти условия реализуются как раз на числах а , близких к «круглым».
192² = 200*184 + 8² = 36864, / (192+8)(192-8)+ 8²/
412² = 400*424 + 12² = 169744, /(412-12)(412+12)+ 12²/
2.3. Возведение в квадрат чисел от 40 до50.
Чтобы возвести в квадрат число пятого десятка (41,42,43,44,45,46,47,48,49),
надо к числу единиц прибавить 15 , затем к полученной сумме приписать квадрат дополнения числа единиц до 10 (если этот квадрат — однозначное число, то перед ним приписывается число о)
43*43=(3 +15 )*100+ 7*7 =1849
48*48=(8 +15 )*100+ 2*2 = 2304
2.4. Возведение в квадрат чисел от 50 до60.
Чтобы возвести в квадрат число шестого десятка (51,52,53,54,55,56,57,58,59)
надо к числу единиц прибавить 25 и к этой сумме приписать квадрат числа единиц.
Например:
54*54=(4+25)*100+4*4=2916
57*57=(7+25)*100+7*7=3249
2.5. Возведение в квадрат числа, оканчивающееся на 5.
Число десятков умножаем на следующее число десятков и прибавляем 25.
15*15 = 10*20+ 25=225 или (1*2 и приписываем справа 25)
35*35 =30*40 +25= 1225 (3*4 и приписываем справа 25)
65*65 = 60*70+25=4225 (6*7 и приписываем справа 25)
2.6. Квадрат числа, оканчивающегося на 1.
При возведении в квадрат числа, оканчивающегося на 1, нужно заменить эту единицу на 0, возвести новое число в квадрат и прибавить к этому квадрату исходное число и число, полученное заменой 1 на 0.
71→70→70 2 =4900→4900+70+71=5041=71 2 .
2.7. Квадрат числа, оканчивающегося на 6.
При возведении в квадрат числа, оканчивающегося на 6, нужно заменить цифру 6 на 5, возвести новое число в квадрат (описанным ранее способом) и прибавить к этому квадрату исходное число и число, полученное заменой 6 на 5.
56→55→55 2 =3025(5 6=30→3025) →3025+55+56 = 3136= 56 2 .
2.8.Квадрат числа, оканчивающегося на 9.
При возведении в квадрат числа, оканчивающегося на 9, нужно заменить эту цифру 9 на 0 (получим следующее натуральное число), возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 9 на 0.
59 → 60→60 2 =3600→ 3600 – 60 – 59 = 3481= 59 2 .
2.9.Квадрат числа, оканчивающегося на 4.
При возведении в квадрат числа, оканчивающегося на 4, нужно заменить цифру 4 на 5, возвести новое число в квадрат и из этого квадрата вычесть исходное число и число, полученное заменой 4 на 5.
84→85→85 2 =7225(8 9=72→7225) →7225 – 85 – 84 = 7056 =84 2 .
2.10. При возведении в квадрат часто бывает удобно воспользоваться формулой (а b) 2 =а 2 +b 2 2аb.
41 2 = (40+1) 2 =1600+1+80=1681.
При выполнении исследовательской работы мне понадобились не только те знания, которые имеются у меня, но и необходимая работа с дополнительной литературой.
1. В ходе моей работы я нашел и освоил различные способы умножения многозначных чисел и могу констатировать следующее — большинство способов умножения многозначных чисел основаны на знании таблицы умножения
— способ «решетчатое умножение» ничуть не хуже, чем общепринятый. Он даже проще, поскольку в клетки таблицы заносятся числа прямо из таблицы умножения без одновременного сложения, присутствующего в стандартном методе;
-«русский крестьянский» способ умножения гораздо проще рассмотренных ранее способов. Но он также очень громоздкий.
Из всех найденных мною необычных способов счета более интересным показался способ «решетчатого умножения или ревность». Я показал его своим одноклассникам, и он им тоже очень понравился.
Самым простым мне показался китайский способ умножения, который использовали китайцы, так как он не требует знаний таблицы умножения. Научившись считать всеми представленными способами, я пришел к выводу: что самые простые способы это те, которые мы изучаем в школе, может быть они для нас более привычны.
2. Я узнал некоторые приемы устного счета, которые помогут мне в жизни. Мне было очень интересно работать над проектом. Я изучил новые для меня способы умножения, рассмотрел различные приемы возведения чисел в квадрат. Многие вычисления связаны с формулами сокращенного умножения, которые я изучил на уроках алгебры. Используя упрощенные приёмы устных вычислений, я теперь могу производить наиболее трудоёмкие арифметические действия без применения калькулятора и компьютера. Заинтересовался не только я, но и мои родители. Я показал приемы устного умножения своим друзьям и одноклассникам. Знание упрощенных приемов устных вычислений особенно важно в тех случаях, когда не имеешь в своем распоряжении таблиц или калькулятора. У меня появилось желание продолжить эту работу и узнать ещё приемы устного счёта. Я думаю, что моя работа не пройдет для меня зря, все полученные знания я смогу использовать при сдаче ГИА и ЕГЭ.
1. Глейзер, Г. И. История математики в школе. – М.: Просвещение, 1964. – 376 с.
2. Перельман Я. И. Занимательная арифметика: Загадки и диковинки в мире чисел. – М.: Издательство 1994. – С. 142-144.
3. Энциклопедия для детей. Т. 11. Математика /Глав. ред. Аксенова М. Д. – М.: Аванта+, 2003. – С. 130-131.
4. Катлер, Э. Система быстрого счета по Трахтенбергу. Мак–Шейн. 1967.
Источник