21 способ решения одной задачи
Муниципальное общеобразовательное учреждение
Лицей №8 «Олимпия»
г. Волгограда, Россия
21 способ решения одной задачи.
учащаяся 6 класса лицея №8 «Олимпия»
Различные способы решения задач……………..…….….
Список источников и литературы.
Введение. Когда ученики решают ту или иную задачу по математике, они обычно не задумывается о том, сколькими способами можно её решить и какой из них будет более рациональным.
Наша исследовательская работа заключалась в том, чтобы узнать сколькими способами можно решить ту или иную задачу и найти более верный способ её решения.
Теоретическая значимость работы заключается в разработке различных способов действий при решении логических.
Практическая значимость заключается в расширении аппарата для решения логических задач. Данный материал можно будет использовать на уроках математики, для того, чтобы ученикам было интересно находить новые способы решения задач.
Метод исследования — поиск, анализ и синтез различных способов решения задач. Объект исследования – логические задачи.
Предмет исследования – различные способы решения логических задач.
Задача: На трёх причалах 156 лодок. Когда из первого причала выплыли 13 лодок, из второго – 6 лодок, а из третьего –17 лодок, то на всех причалах лодок стало поровну. Сколько лодок было на третьем причале первоначально?
1 способ: краткая запись задачи.
Было Выплыло Осталось
1 причал — ? л. 13 л. ? л.
2 причал — ? л всего 156 л. 6 л. ? л.
3 причал — ? л. 17 л. ? л.
2 способ: схематический чертеж задачи.
1)13 + 6 = 19 (л.) – выплыло из I и II причалов
2) 19 + 17 = 36 (л.) – выплыло из трех причалов
3) 156 – 36 = 120 (л.) – осталось на трех причалах
4)120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 +17 = 30 (л.) – выплыло из I и III причалов
2) 30 + 6 = 36 (л.) – выплыло из трех причалов
3) 156 – 36 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 6 + 17 = 23 (л.) – выплыли из II и III причалов
2) 23 + 13 = 36 (л.) – выплыло из трех причалов
3) 156 – 36 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 + 6 = 36 (л.) – выплыло из трех причалов
2) 156 – 36 = 120 (л.) – осталось на трех причалах
3) 120 : 3 = 40 (л.) – осталось на каждом причале
4) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 13 = 143 (л.) – остались на трёх причалах после выплыва из первого причала
2) 143 – 6 = 137 (л.) – осталось на трёх причалах после выплыва из первого и второго причалов
3) 137 – 17 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 13 = 143 (л.) – остались на трёх причалах после выплыва из первого причала
2) 143 – 17 = 126 (л.) – осталось на трёх причалах после выплыва из первого и третьего причалов
3) 126 – 6 = 120 (л.) – осталось на трёх причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 6 = 150 (л.) — осталось на трёх причалах после выплыва из второго причала
2) 150– 13 = 137 (л.) – осталось на трёх причалах после выплыва из второго и первого причалов
3) 137 – 17 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 6 = 150 (л.) – осталось на трёх причалах после выплыва из второго причала
2) 150– 17 = 133 (л.) – осталось на трёх причалах после выплыва из второго и третьего причалов
3) 133 – 13 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 17 = 139 (л.) – осталось на трёх причалах после выплыва из третьего причала
2) 139 – 13 = 126 (л.) осталось на трёх причалах после выплыва из третьего и первого причалов
3) 126 – 6 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 156 – 17 = 139 (л.) – осталось на трёх причалах после выплыва из третьего причала
2) 139 – 6 = 133(л.) – остались на трёх причалах после выплыва из третьего и второго причалов
3) 133 – 13 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 51 (л.) – было на третьем причале первоначально
1) 6 + 17 = 23 (л.) – выплыли из II и III причалов
2) 156 – 13 = 143 (л.) – остались на трёх причалах после выплыва из первого причала
3) 143 – 23 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 +17 = 30 (л.) – выплыло из I и III причалов
2) 156 – 6 = 150 (л.) – осталось на трёх причалах после выплыва из второго причала
3) 150 – 30 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 + 6 = 19 (л.) – выплыло из I и II причалов
2) 156 – 17 = 139 (л.) – осталось на трёх причалах после выплыва из третьего причала
3) 139 – 19 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 + 6 = 19 (л.) – выплыло из I и II причалов
2) 156 – 19 = 137 (л.) – осталось на трёх причалах после выплыва из первого и второго причалов
3) 137 – 17 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 13 + 17 = 30 (л.) – выплыло из I и III причалов
2) 156 – 30 = 126 (л.) – осталось на трёх причалах после выплыва из первого и третьего причалов
3) 126 – 6 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
1) 6 + 17 = 23 (л.) – выплыли из II и III причалов
2) 156 – 23 = 133 (л.) – осталось на трёх причалах после выплыва из второго и третьего причалов
3) 133 – 13 = 120 (л.) – осталось на трех причалах
4) 120 : 3 = 40 (л.) – осталось на каждом причале
5) 40 + 17 = 57 (л.) – было на третьем причале первоначально
Существуют и другие способы решения данной задачи.
3 способ: графическая модель задачи.
В этих вариантах решения сначала надо определить, сколько лодок было бы на всех трёх причалах первоначально, если бы на каждом из них лодок было столько, сколько на третьем причале.
1) 17– 13 = 4 (л.) – добавить на первый причал, чтобы лодок было одинаково, как на третьем причале
2) 17 – 6 = 11 (л.) – добавить на второй причал, чтобы лодок было одинаково, как на третьем причале
3) 4 + 11 = 15 (л.) – добавили на первый и второй причалы
4) 156 + 15= 171 (л.) – стало на трёх причалах
5) 171 : 3 = 57 (л.) – было на третьем причале первоначально
1) 17 – 6 = 11 (л.) – добавить на второй причал, чтобы лодок было одинаково, как на третьем причале
2) 17 – 13 = 4 (л.) – добавить на первый причал, чтобы лодок было одинаково, как на третьем причале
3) 156 + 11= 167 (л.) – стало на трёх причалах после добавления на второй причал
4) 167 + 4= 171 (л.) – стало на трёх причалах после добавления на третий причал
5) 171 : 3 = 57 (л.) – было на третьем причале первоначально
1) 17 – 13 = 4 (л.) – добавить на первый причал, чтобы лодок было одинаково, как на третьем причале
2) 17 – 6 = 11 (л.) – добавить на второй причал, чтобы лодок было одинаково, как на третьем причале
3) 11 + 4 = 15 (л.) – добавили на первый и второй причалы
4) 156 + 15 = 171 (л.) – стало на трёх причалах
5) 171 : 3 = 57 (л.) – было на третьем причале первоначально
1) 17 – 13 = 4 (л.) – добавить на первый причал, чтобы лодок было одинаково, как на третьем причале
2) 17 – 6 = 11 (л.) – добавить на второй причал, чтобы лодок было одинаково, как на третьем причале
3) 156 + 11= 167 (л.) – стало на трёх причалах после добавления на второй причал
4) 167 + 4 = 171 (л.) – стало на трёх причалах
5) 171 : 3 = 57 (л.) – было на третьем причале первоначально
1) 17 – 13 = 4 (л.) – добавить на первый причал, чтобы лодок было одинаково, как на третьем причале
2) 17 – 6 = 11 (л.) – добавить на второй причал, чтобы лодок было одинаково, как на третьем причале
3) 156 + 4= 160(л.) – стало на трёх причалах после добавления на первый причал
4) 160 + 11 = 171 (л.) – стало на трёх причалах
5) 171 : 3 = 57 (л.) – было на третьем причале первоначально
В итоге исследований, мы выявили 21 способ решения данной задачи.
Существует множество способов, которые используются при решении текстовых логических задач.
Способы решения задач часто имеют практический характер, что немаловажно в современной жизни. Они заставляют задумываться, подходить к решению какой-либо проблемы с разных сторон, уметь выбирать из множества способов решения наиболее простой, легкий путь.
Поиск задач, самостоятельное описание, поиск новых и интересных способов их решения, а также попытки рассмотрения другой формы представления данных условия позволили нам решить поставленные задачи.
Мы ознакомили наших одноклассников с проведёнными исследованиями, и теперь решать логические задачи для них намного интересней и веселей
Данная тема, безусловно, расширяет математический кругозор учащихся, обогащает арсенал средств, используемых в решении разнообразных логических задач.
1. Задачи для внеклассной работы по математике в V – VI классах: Пособие для учителей [Текст]/ Сост. . Под ред. , . М.: МИРОС, 1993. с. 42. – ISBN -4
2. Занимательная математика. 5 – 11 классы. [Текст]: (Как сделать уроки нескучными) / Авт. – сост. . Волгоград: Учитель, 2005. с.32-38. – 10000 экз. –-8
3. Депман, И.Я., Виленкин, Н. Я. За страницами учебника математики Пособие для учащихся 5 – 6 кл. [Текст]/ И. Я Депман. М.: Просвещение, 1999. с. 189 – 191, 231. – 10000 экз. – ISBN -1
4. Смыкалова, главы по математике для учащихся 5 класса. [Текст]: СПб: СМИО Пресс, 2009. с.14-20. – 2000 экз. – ISBN -2
5. Фарков, олимпиады в школе.5–11 классы.[Текст] / . М.: Айрис–пресс, 2007. с. 27, 34, 61. – 7000 экз. – ISBN 2394-7
Источник
Решение одной задачи различными способами
В педагогической и методической литературе общепринятым является мнение, что решение задач разными способами является эффективным педагогическим приемом, поскольку это способствует повышению уровня математических знаний и умений учащихся, развитию их исследовательских способностей, пробуждает творческую фантазию и интерес к изучению математики.
Однако, если данный прием применять бессистемно и неорганизованно, решая каждый раз, когда это возможно, задачи разными способами, то это может привести и к обратному результату: потере у учащихся интереса к изучаемому, неосознанности выполняемых ими действий, бесполезной трате времени. Перед тем, как предложить учащимся какую-либо задачу, учитель должен досконально изучить ее сам: установить возможные связи с другими задачами, отыскать различные способы решения и выявить целесообразность рассмотрения этих способов для конкретной педагогической ситуации.
На одну задачу, решаемую разными способами, можно смотреть как на своеобразную систему, удовлетворяющую всем предъявляемым к ней требованиям. Такие системы задач в зависимости от типа или этапа урока, специфики рассматриваемых способов решения позволяют добиться различных целей при условии правильной организации работы с ними.
Выделим основные цели решения одной задачи разными способами или методами.
1. Выявление межпредметных связей: алгебра – геометрия, тригонометрия – геометрия и др.
2. Обобщение и систематизация полученных знаний, установление взаимосвязей между различными теоретическими фактами.
3. Выявление сущности определенных методов, их отличительных черт, достоинств и недостатков при применении к конкретным классам задач.
4. Вооружение учащихся различными методами решения задач с целью обретения ими уверенности в своих силах, возможности в случае затруднения перейти к другому приему решения.
5. Демонстрация рациональности, эффективности и изящества одних и нерациональности и порою ошибочности других способов.
6. Показ учащимся одного из приема самоконтроля.
В соответствии с выделенными целями определяются целесообразность и место данных систем задач в учебном процессе, разрабатывается методика их применения и решения.
Рассмотрим на конкретных примерах, как решение одной задачи разными способами или методами может помочь в осуществлении каждой из перечисленных целей.
Выявление межпредметных связей способствует осознанному усвоению учащимися материала, убеждению их в силе математических методов, которые могут быть использованы в разных областях знаний. Поэтому имеет смысл проводить интегрированные уроки, например, алгебры и геометрии.
Пример 1. Вычислите 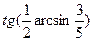
Способ 1 (алгебраический).
Пусть 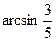
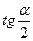
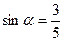
Воспользуемся формулой понижения степени:
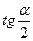
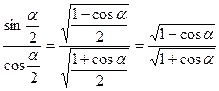
Вычисляя 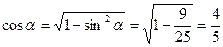
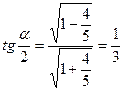
Способ 2 (геометрический).
Воспользуемся понятиями синуса и тангенса острого угла прямоугольного треугольника, теоремой Пифагора и свойством биссектрисы треугольника.
 | В прямоугольном треугольнике АВС ( 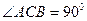 ) ВС=3, АВ=5 и АК – биссектриса угла ВАС. По теореме Пифагора АС=4, а по свойству биссектрисы треугольника СК= ) ВС=3, АВ=5 и АК – биссектриса угла ВАС. По теореме Пифагора АС=4, а по свойству биссектрисы треугольника СК= 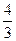 . Получаем, что . Получаем, что 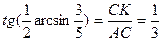 . . |
Важно также сопоставлять арифметический и алгебраический способы решения одной и той же задачи.
Известно, что задачи на концентрацию вызывают значительные затруднения у учащихся. Если же показать им некоторые арифметические способы их решения, то это поможет учащимся осознать основные идеи, используемые при решении задач данного вида.
Пример 2. Имеется лом стали двух сортов, причем первый сорт содержит 10% никеля, а второй 30%. На сколько тонн стали больше нужно взять второго сорта, чем первого, чтобы получить 200 т стали с содержанием никеля 25%?
Способ 1 (алгебраический).
Пусть первого сорта нужно взять х тонн, а второго у тонн. Тогда в стали первого сорта содержится 0,1х тонн никеля, а в стали второго сорта 0,3у тонн никеля. Поскольку в новом сплаве никеля стало 25%, т.е. 0,25·200 = 50 т, то получим следующую систему уравнений:
Из этой системы находим, что х=50, а у=150. Значит, стали второго сорта нужно взять на 100 тонн больше.
Способ 2 (арифметический).
Найдем разность между процентным содержанием никеля в каждом из двух сортов стали и полученном сплаве:
25% – 10% = 15%, 30% – 25% = 5%.
Полученные результаты показывают, что 10%-ного сплава следует взять 5 частей, а 30%-ного – 15 частей. Отсюда легко находится, что нужно взять 50 тонн стали первого сорта и 150 тонн стали второго сорта.
Таким образом, получаем более простой и изящный способ решения задачи, который может применяться при решении подобных задач.
При обобщении и систематизации знаний решение задач разными способами позволяет охватить большой теоретический материал, установить связи между изучаемыми понятиями и фактами.
Пример 3. Найдите радиус окружности, вписанной в равнобедренный треугольник с основанием 10 и боковой стороной 13.
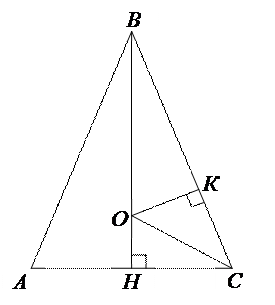 | Способ 1 (использование свойства биссектрисы треугольника). По теореме Пифагора находим, что ВН = 12. Из треугольника ВСН имеем 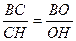 , т.е. , т.е. 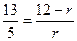 . Отсюда, . Отсюда, 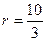 . . |
Способ 2 (использование понятия синуса острого угла прямоугольного треугольника).
Из треугольника ВСН находим 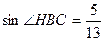
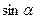
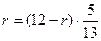
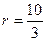
Способ 3 (использование свойства отрезков касательных, проведенных из одной точки к окружности).
Согласно указанному свойству, СН = СК = 5. Значит, ВК = 13 – 5 = 8.
Из треугольника ВКО по теореме Пифагора имеем:
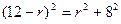
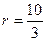
Способ 4 (использование формулы S=pr).
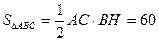
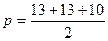
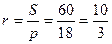
Для достижения третьей цели, т.е. выявления сущности отдельных методов необходима их демонстрация на какой-либо одной задаче. Обычно разные методы демонстрируют на разных задачах, учитывая при этом, какой из них в каждом конкретном случае более эффективен. При таком подходе метод может невольно связаться с самой задачей, а его сущность и значимость остается на втором плане. Когда же разные методы испробованы на одной задаче, то у учащихся появляется возможность оценить их, сравнить, уяснить их особенности. Рассмотрим пример, когда к геометрической задаче применяется векторный, координатный и собственно геометрический методы решения.

Пример 4. Докажите, что в прямоугольном треугольнике длина медианы, проведенной к гипотенузе, равна ее половине.
Метод 1 (векторный).
Пусть в прямоугольном треугольнике 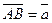 , , 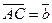 . Тогда медиана . Тогда медиана 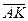 по правилу сложения векторов равна по правилу сложения векторов равна 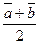 , а гипотенуза , а гипотенуза 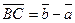 , значит , значит 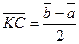 . Необходимо доказать, что длины векторов . Необходимо доказать, что длины векторов 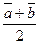 и и  равны, т.е. равны, т.е. 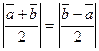 или или 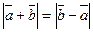 . . |  |
Возведем обе части этого равенства в квадрат: 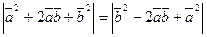

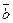
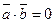
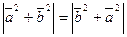
Таким образом, 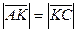
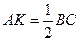
Метод 2 (координатный).
Примем точку А за начало прямоугольной системы координат, а стороны АВ и АС поместим на координатных осях.
Имеем: В (0;у), С (х;0). Поскольку К — середина отрезка ВС, то К ( 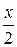 ; ; 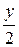 ). Найдем длину отрезка АК: ). Найдем длину отрезка АК: 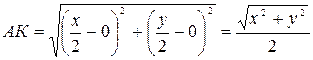 . Найдем длину отрезка ВС: . Найдем длину отрезка ВС: 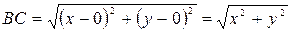 . . 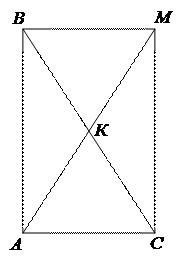 Получаем, что Получаем, что 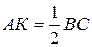 . . |
Чтобы учащиеся были уверены в своих силах при решении задач и могли переходить от одного приема к другому, необходимо уже при объяснении нового материала рассматривать несколько способов получения верного результата. Пример 5. Решите уравнение: Способ 1 (аналитический). Данное уравнение равносильно совокупности двух систем: При решении этой совокупности получаем корни: Способ 2 (замена переменной). Применяя свойство модуля Способ 3 (функциональный). Функция Получаем: Для достижения пятой цели необходимо подбирать такие задачи, способы решения которых значительно отличаются в плане их эффективности и рациональности, либо задачи, позволяющие выявить некорректность отдельного способа с целью получения важных теоретических выводов. Пример 6. Решите уравнение: Если предложить учащимся самостоятельно решить данное уравнение, то они могут воспользоваться различными преобразованиями /1/. Откуда Получаем, что Если в каждом из трех способов решения сделать проверку, то получим, что Итак, мы рассмотрели несколько примеров решения задач разными способами. Еще раз обратим внимание на то, что их специфика зависит от целей, поставленных учителем. Теперь обратимся к методике использования таких систем задач на уроках математики. Очевидно, что особенности методики также связаны с целями решения одной задачи разными способами. Для достижения первой цели, т.е. выявления межпредметных связей, необходимо на первых порах проводить интегрированные уроки. На таких уроках рассматриваются две-три задачи, решаемые разными способами. При этом не следует перед учащимися просто ставить проблему отыскания нескольких способов решения. Нужно четко указать им, что данная задача имеет несколько приемов решения (например, алгебраический и геометрический), а затем подробно остановиться на каждом из них. Если у учащихся возникают трудности, то учитель может наводящими вопросами подвести их к идее решения. В дальнейшем, когда у учащихся сформируется определенный навык перехода от одной области знаний к другой, можно отказаться от интегрированных уроков. Выявление межпредметных связей следует проводить на обычном уроке, предлагая учащимся самостоятельно найти несколько способов решения одной задачи. При обобщении и систематизации знаний помощь учителя в отыскании разных способов решения одной задачи должна быть минимальной. Необходимо четко поставить перед учащимися цель: решить задачу двумя, тремя, четырьмя и т.д. способами. Работа может проходить самостоятельно или в группах. При самостоятельной работе учащимся дается определенное время на решение задачи, после чего, каждый из них сообщает, сколько способов ее решения им было найдено. Затем к доске вызывается любой из учащихся, нашедших только один способ решения задачи, и демонстрирует его. После этого учитель выясняет, кто еще из учащихся «увидел» этот способ, и вызывает к доске следующего учащегося для показа другого способа и т.д. Примерно так же может быть построена работа в группах. Каждая группа ищет как можно больше способов решения какой-либо задачи, после чего подводятся итоги, и происходит демонстрация способов. В классах с невысоким уровнем подготовки учитель каждой группе может дать задание решить задачу каким-то конкретным способом. Затем представители групп показывают свои способы решения, происходит обсуждение их достоинств и недостатков. Если поставлена цель ознакомить учащихся с различными методами решения задач, то на первых порах самостоятельность учащихся минимальна. Сначала учитель показывает сущность основных методов, приводит различные примеры. Следующим важным шагом является демонстрация применения различных методов при решении одной и той же задачи. Это позволит учащимся сопоставить изученные методы, провести их сравнительную характеристику, выявить преимущества того или иного методы при решении определенных задач. Когда учащиеся в достаточной мере овладеют различными методами решения задач, необходимо увеличить степень их самостоятельности. Учащиеся должны при минимальной помощи учителя уметь применять разные методы к решению одной задачи, делать выводы о целесообразности их использования в каждом конкретном случае, грамотно аргументировать свою позицию. Для достижения четвертой цели учителю необходимо уже при объяснении нового материала вводить различные способы решения одного и того же типа задач (например, аналитический и графический способы решения уравнений с параметром). В классах с высоким уровнем подготовки учащиеся могут принимать непосредственное участие в поиске таких способов. В классах с невысоким уровнем подготовки учитель сам демонстрирует разные способы решения какого-то вида задач. И в том, и в другом случае необходимо, чтобы учащиеся проанализировали и сопоставили возможные способы, выявили их достоинства и недостатки. Полезно предлагать учащимся задания по предварительному выбору способа решения той или иной задачи в зависимости от ее содержания. В случае, когда необходимо выявить рациональность и правильность отдельных способов решения задачи, учащимся дается самостоятельное задание по поиску этих способов. Такая работа с одной стороны развивает исследовательские способности учащихся, а с другой – позволяет осознать ошибочность каких-либо действий. Так при решении логарифмического уравнения (пример 6) и разборе возможных способов используемых преобразований, учитель может организовать дискуссию, в процессе которой поднимаются вопросы о равносильности уравнений и тождественных преобразованиях, нарушающих ОДЗ уравнения. Такой прием будет гораздо более эффективным, чем просто озвучивание учителем этих вопросов. Знания, полученные учащимися при такой работе, станут осознанными и прочными. Таким образом, методика использования педагогического приема решения одной задачи разными способами в значительной степени зависит от поставленных целей. Вопросы и задания 1. В чем выражается эффективность использования такого педагогического приема как решение одной задачи разными способами? 2. С какими целями можно связать решение одной задачи разными способами? 3. В чем выражается сущность каждой из этих целей? 4. Каковы характерные особенности методики использования приема решения одной задачи разными способами? 5. В каких случаях учащиеся принимают активное участие в поиске различных способов решения задачи? 6. Решите задачи разными способами: 1) В равнобедренном треугольнике АВС АВ=6, АС=ВС=5. Найдите радиус описанной окружности. 2) В равнобедренном треугольнике АВС АВ=16, АС=ВС=10. Найдите длину медианы АМ. 3) В треугольник АВС вписана окружность, которая точкой касания делит сторону ВС на отрезки, длиной 5 и 9 см. Найдите радиус окружности, если 4) Решите уравнение: 7. Приведите пример решения одной задачи разными способами при выявлении межпредметных связей: алгебра-геометрия, тригонометрия-геометрия. 8. Определите, какой цели соответствует решение уравнения 9. Подберите любое уравнение с параметром, которое решается несколькими способами. Опишите методику использования полученной системы задач. 10. Решите задачи к любому параграфу учебника «Геометрия 7-9» под ред. Л.С. Атанасяна и выделите те из них которые решаются разными способами. Рассмотрите эти способы. Рассмотреть различные способы доказательства свойства биссектрисы треугольника в статье Амелькиной Г. Несколько решений одной задачи. Свойство биссектрисы треугольника. / Газета «Первое сентября. Математика», 2005. – № 1. – с.18-24. 11. Составьте библиографию статей по теме за последние 20 лет в журнале «Математика в школе», газете «Первое сентября. Математика». Нам важно ваше мнение! Был ли полезен опубликованный материал? Да | Нет Источник |





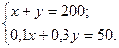


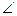 А=90 0 , то АВМС – прямоугольник, значит ВС=АМ. Получаем, что
А=90 0 , то АВМС – прямоугольник, значит ВС=АМ. Получаем, что 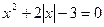 .
.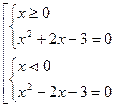
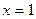 и
и 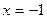 .
.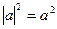 , перепишем уравнение в следующем виде:
, перепишем уравнение в следующем виде: 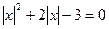 . Сделаем замену:
. Сделаем замену: 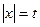 ,
, 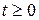 Получим уравнение:
Получим уравнение: 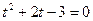 , откуда
, откуда 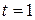 ,
, 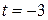 . Имеем:
. Имеем: 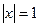 , т.е.
, т.е. 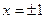 .
.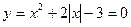 является четной. Тогда решим уравнение для
является четной. Тогда решим уравнение для  . Получим
. Получим 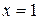 . И возьмем корень, ему симметричный:
. И возьмем корень, ему симметричный: 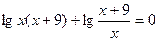 .
.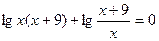 ,
,  ,
, 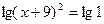 ,
, 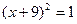 .
.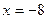 или
или  .
.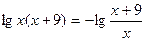 ,
, 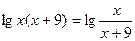 ,
, 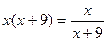 .
.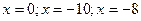
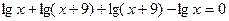 ,
, 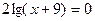 .Ответ.
.Ответ. 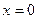 и
и 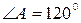 .
.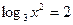 .
.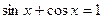 четырьмя способами: возведением обеих частей уравнения в квадрат, введением вспомогательного аргумента, методом универсальной подстановки, разложением на множители. Отыщите эти способы и опишите методику использования полученной системы задач.
четырьмя способами: возведением обеих частей уравнения в квадрат, введением вспомогательного аргумента, методом универсальной подстановки, разложением на множители. Отыщите эти способы и опишите методику использования полученной системы задач.


